初中数学教学中几何直观能力培养探析

摘 要：几何直观素养是数学核心素养的重要组成部分，属于深层次学习目标.在初中数学教学中，培养学生的几何直观素养，有助于学生顺利找出几何问题中隐含的数量关系和位置关系，使复杂、抽象的问题简单化和形象化，最终促使学生更好地理解、掌握数学知识.基于此，本文简述了几何直观能力的内涵，并结合课堂教学实践，针对学生几何直观能力的培养路径展开探究，旨在培养学生的几何直观能力，提升学生的数学核心素养.

关键词：初中数学；课堂教学；几何直观能力；核心素养

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2024）29-0011-03

收稿日期：2024-07-15

作者简介：崔春红（1984.2—），女，江苏省东台人，本科，中学一级教师，从事初中数学教学研究.

《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）立足于数学学科特征，明确提出了“数学核心素养”的培养目标.几何直观作为数学核心素养的重要组成部分，有助于学生更好地把握数学问题的本质，明晰思维路径，继而实现学生的全面、长远发展.与此同时，《课程标准》聚焦7～9年级学生的学习特点，提出了“形成推理能力、发展空间观念和几何直观”的教学目标.因此，《课程标准》对初中生的几何直观能力提出了更高的要求.但在当前初中数学教学中，几何直观能力培养依然存在较大的误区和问题.例如，对几何直观素养认知不够全面、几何直观教学方式单一等，致使学生的几何直观能力低下，难以满足新课程的学习要求.基于此，初中数学教师必须及时更新教学理念，重视几何直观素养教学，并结合初中生的学习特点，积极推进教学模式创新，不断提升学生的几何直观素养.

1 几何直观能力培养的重要性

“几何直观”是《课程标准》提出的核心概念之一，主要是借助图形描述问题、分析问题.在初中数学学习活动中，几何直观可使原本复杂的数学问题更加简单、形象，学生能够更好地分析、探索问题，在明确思路的基础上预测结果.具体来说，就是在数学教学活动中，几何直观能力能够借助图形、实物、模型和物体的位置关系、数量关系，将空间形式、数量关系直接展示出来，以便于学生在直接感知的基础上，体会其中蕴含的本质属性，继而形成分析问题和解决问题的能力［1］.

新课程改革背景下，培养初中生的几何直观能力已成为当前教学的重中之重.一方面，有助于学生理解抽象的数学概念.在数学教学中培养学生的几何直观能力，可为学生创造思考的机会，学生在面对复杂问题时，能够通过思考逐渐形成独立的见解，进而通过推理、分析、总结和归纳等学习过程，轻松理解抽象的数学概念.另一方面，有助于培养学生的洞察力，促使学生深层次思考，学生在学习中能够由点到面地看待问题，逐渐接近数学问题的本质.因此，发展学生的几何直观能力，可推进学生的思考层次，拓展其思考维度，在深入分析问题、探索问题本质的过程中提升学生核心素养.

2 几何直观能力的培养策略

2.1 联系生活实际，发展几何直观能力

几何直观作为数学领域最为重要的概念之一，主要是借助图形展开数学思考和数学想象.由于学生理解知识的能力有限，在培养其几何直观素养时面临着一定的困难.基于此，教师可立足于数学学科特征，从学生的实际生活出发，依托生活中的实物帮助学生形成直观的视觉体验，在脑海中逐渐形成形象、立体的几何图形，进而促使学生在理解抽象的数学知识点的同时，实现数学思维的深度发展，为学生更好地开展学习奠定基础［2］.

例如，在学习“三视图”时，为了培养学生的几何直观能力，在课堂教学过程中，教师首先给学生展示两张庐山的照片，让学生在真切的感知中体会“横看成岭侧成峰，远近高低各不同”的内涵，学生初步认识到：在对同一个物体进行观察时，观察的角度不同，视图也有所不同.接着，为了进一步发展学生的几何直观能力，教师可拿出事先准备的字典，并借助

信息技术手段，将其正面、侧面、上面依次展示在学生面前，使学生在观察中对“三视图”的内涵形成更加深刻的认识，并在实物的辅助下，更好地展开想象，在学习中逐渐形成一定的几何直观能力.“三视图”是培养学生几何直观能力的最佳切入点，同时也是学生难以理解的知识点.在教学活动中，教师从实际生活出发，借助庐山不同视角的风景图，激活学生的探究兴趣，引导学生快速进入到本节课学习中.之后，通过观察实物，学生在直观的感知中体会“三视图”的内涵，从而促进其几何直观能力的发展.

2.2 依托信息技术，增强几何直观能力

《课程标准》明确提出促进信息技术与数学课程融合.要求教师在开展课堂教学时，应结合具体的教学内容，科学融入现代信息技术，为学生打造现代化的数学课堂.

初中阶段的学生正处在从具体向形象思维过渡的重要阶段，尚未形成良好的空间观念、推理能力，几何直观素养低下.基于此，为了培养学生的几何直观能力，在课堂教学时，教师可充分利用多媒体信息技术，依托几何画板、超级画板等动态数学软件，将问题中点、线、面的运动过程直观地展示出来，促使学生在直观感知中理解图形的形成过程，从而促进其几何直观能力的发展.

例如，在学习“图形的旋转”时，鉴于本章节中知识点的特殊性，要求学生必须具备较强的空间想象能力，方可高效达成预期的学习目标.在开展课堂教学时，仅仅依赖课本中的图片，学生很难想象图形是如何旋转的，或者图形经过旋转之后会得到什么样的图形.面对这一现象，在开展课堂教学时，教师可充分借助信息技术工具，以视频的形式将图形的旋转过程直观地呈现出来.如此，学生通过观看视频，就可直接看到不同图形的旋转过程，对其形成过程的认识更加深刻.之后，教师可指导学生围绕某一个图形展开探究，对其旋转的运动规律归纳总结.如此，借助现代信息技术手段，将原本比较抽象的数学知识变得形象直观，学生在深刻理解这一知识点的同时，提升其几何直观能力.

2.3 开展实践操作活动，培养几何直观能力

与传统的课堂教学模式相比，实践操作活动可强化学生的学习体验，活跃学生的思维，有助于学生在动手的过程中，对数学知识形成深刻的认识.对此，《课程标准》也倡导学生通过动手“折一折、画一画、剪一剪、拼一拼”等操作活动获取数学知识.基于此，在初中数学教学中，教师可结合教学实际情况，指导学生积极开展实践操作，在动手实践活动中学习数学知识，从而更深刻地理解数学知识，并由此促进学生几何直观能力的发展［3］.

例如，在学习“轴对称”时，由于其属于“图形的变化”范畴，要求学生理解轴对称的基本概念与性质，并理解几何图形的对称性，感悟生活中的对称美，进而在学习中提升几何直观能力.基于此，在组织课堂教学时

，一方面，教师可借助多媒体信息技术

展示几何图形，指导学生对其进行观察，并思考其特征，使学生初步感知轴对称图形的形成过程；另一方面，教师可结合本章节教学内容设计“折一折、画一画”实践活动，指导学生先将长方形纸片进行对折，之后在其上面用笔尖刺出一个图形，由此学生能够得到两个完全相同的图形，它们关于折痕成轴对称.最后，教师可为学生提供一个图形，要求学生根据轴对称的特点，画出它关于某一条直线对称的图形.在这一学习过程中，学生通过动手实践，能够精准把握轴对称图形的特点，由此促进其几何直观能力的发展.

2.4 注重数形结合，强化几何直观能力

数形结合是数学学习中非常重要的一种思想方法.从本质上来说，“数”与“形”代表着同一事物的两个方面，这两个方面是密不可分的，具有一定的关联性.就数学来说，数形结合思想就是将数学知识中的文字语言、数量关系进行转化，使其成为一种直观的图形，旨在促进数学问题具体化、形象化，便于学生在灵活转化中理解数学知识的本质，最终深层理解数学知识，并逐渐形成一定的数学思维.数形结合思想虽然和几何直观能力存在相同之处，但并不是一回事.数形结合是一种解决问题的思想方法，几何直观则是一种直观感知，是一种数学能力.在初中数学课堂教学中，通过“数”与“形”之间的转化，学生可根据语言、文字、符号描述，画出所对应的几何图形，并在化“数”为“形”的思考中，推动学生几何直观能力的发展.因此，在组织课堂教学时，教师必须立足于“数”和“形”之间的内在联系，指导学生从“数”和“形”两个角度思考问题，精准把握二者之间的转化关系［4］.

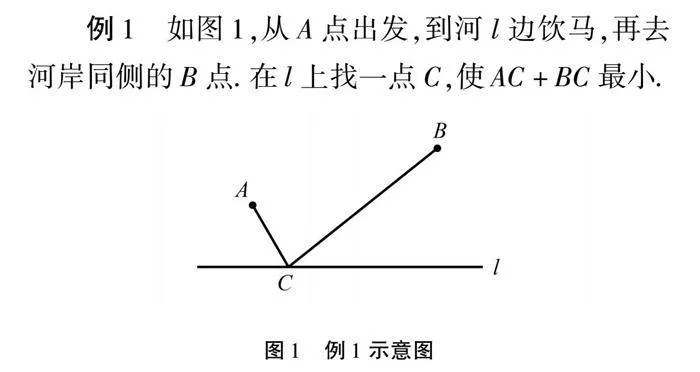
例1 如图1，从A点出发，到河l边饮马，再去河岸同侧的B点.在l上找一点C，使AC+BC最小.

这是一道典型的“将军饮马”问题.在组织课堂教学时，为了培养学生的几何直观能力，教师可借助数形结合思想，指导学生阅读题目内容，并从中抽象出“求两条线段之和的最小值”问题，之后再利用轴对称相关知识点进行解决.在解决问题的过程中，学生的建模能力、几何直观能力也随之提升.

为了促进几何直观能力的进一步发展，教师可对这一题目展开延伸.

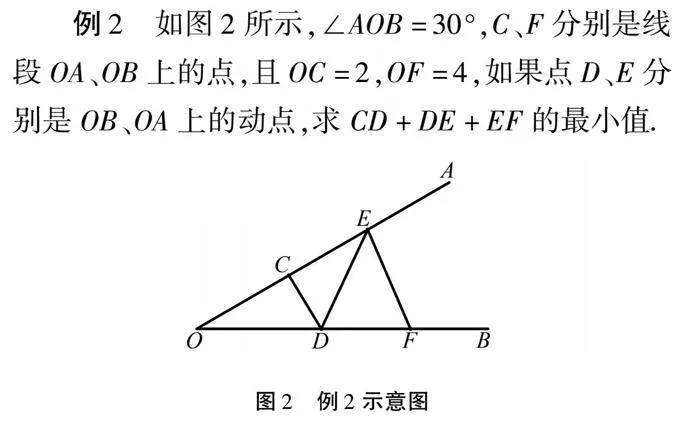
例2 如图2所示，∠AOB=30°，C、F分别是线段OA、OB上的点，且OC=2，OF=4，如果点D、E分别是OB、OA上的动点，求CD+DE+EF的最小值.

如此一来，通过“将军饮马”问题的拓展和延伸，学生能够在利用数形结合思想解决问题的过程中，促进几何直观能力的发展，并逐渐形成利用几何直观解决问题的数学思维.

3 结束语

新课程改革背景下，培养学生的几何直观能力是全面提升学生学习效果、促进学生全面发展的必然选择.基于此，在初中数学教学中，教师必须立足几何直观能力的内涵，积极推进课堂教学改革.在课堂教学过程中，联系生活实际，发展学生的几何直观能力；依托信息技术，增强学生的几何直观能力；通过动手“折一折、画一画、剪一剪、拼一拼”等实践操作活动，培养学生的几何直观能力，并在数形结合思想渗透过程中促进学生几何直观素养的发展.

参考文献：［1］ 李思莹.初中数学活动中发展学生几何直观能力的实践探析［J］.新智慧，2024（9）：79-81.

［2］ 张秋婷.创新初中数学教学 发展学生数学素养：以培育学生几何直观能力为例［J］.新课程，2024（2）：142-144.

［3］ 鲁艳.初中数学教学中几何直观能力培养探析［J］.求知导刊，2023（31）：95-97.

［4］ 于会祥，崔燕燕.初中数学教学中几何直观能力的培养方法［J］.新课程教学（电子版），2023（16）：90-91.

［责任编辑：李 璟］