高中物理动力学临界问题的解题策略

摘要：通过对绳子断裂的临界问题、分离类临界问题、相对滑动的临界问题等问题的研究，探讨了高中物理中动力学临界问题的解题策略.通过对相关临界条件的寻找和探索、常见类型的归纳以及具体实例的详细分析，总结出了各类临界问题的解题方法和技巧，旨在帮助高中生更好地理解和掌握这一重要物理知识领域，提高解题能力和物理思维水平.

关键词：动力学；临界问题；解题策略

中图分类号：G632文献标识码：A文章编号：1008-0333（2024）28-0114-03

在高中物理的学习中，动力学临界问题一直是学生感到困难但又十分重要的内容.这类问题常常涉及物体运动状态的突变，需要准确把握临界条件，运用恰当的物理规律和数学方法进行求解.

1绳子断裂的临界问题

例1如图1所示，矩形盒内用两根不可伸长的轻线固定一个质量为m=0.6 kg的匀质小球，a线与水平方向成37°角，b线水平.两根轻线所能承受的最大拉力都是Fm=15 N，已知sin37°=0.6，cos37°=0.8，取g=10 m/s2，则（）.

A.系统静止时，a线所受的拉力大小12 N

B.系统静止时，b线所受的拉力大小8 N

C.当系统沿竖直方向匀加速上升时，为保证轻线不被拉断，加速度最大为5 m/s2

D.当系统沿水平方向向右匀加速时，为保证轻线不被拉断，加速度最大为10 m/s2

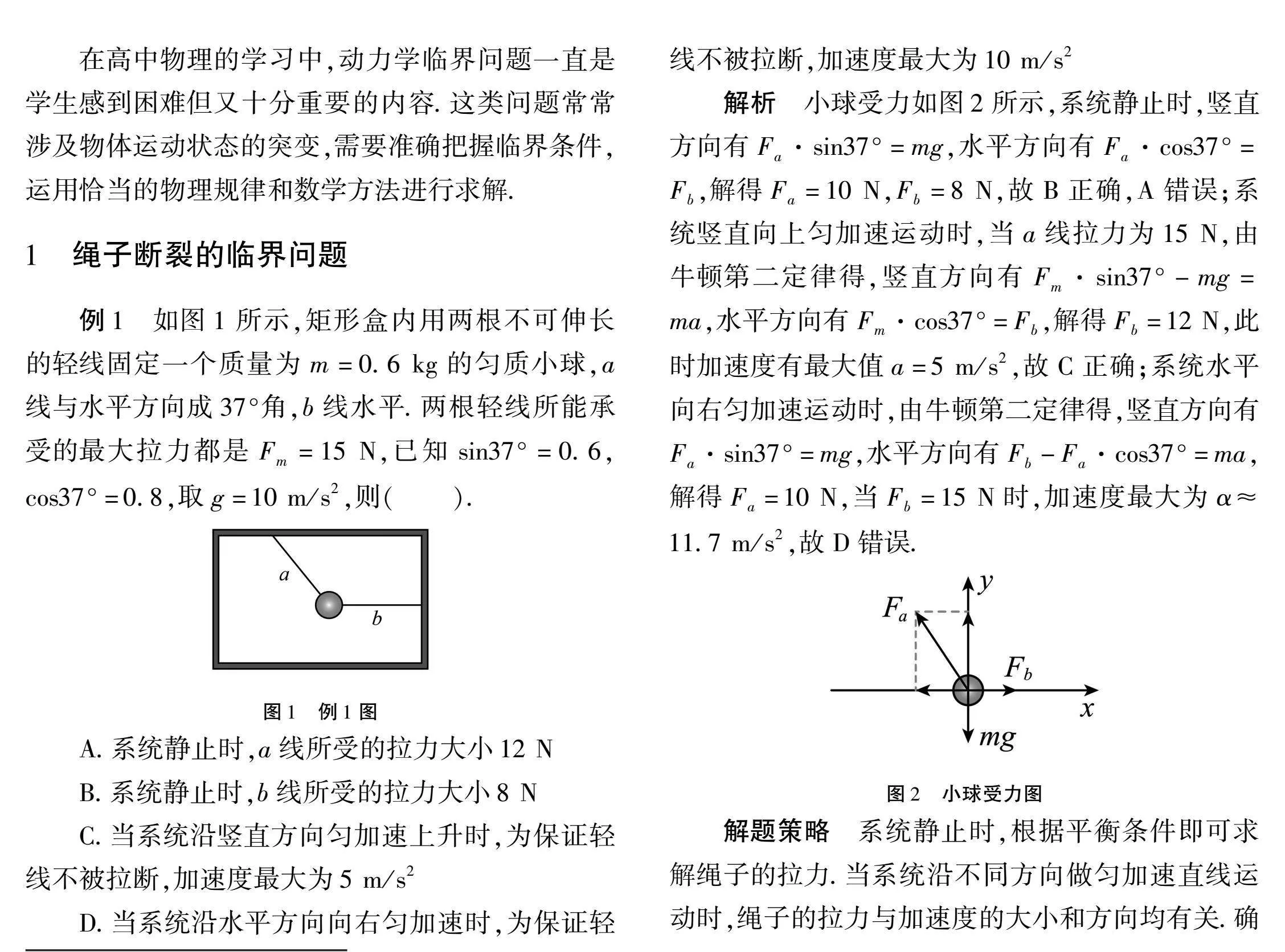
解析小球受力如图2所示，系统静止时，竖直方向有Fa·sin37°=mg，水平方向有Fa·cos37°=Fb，解得Fa=10 N，Fb=8 N，故B正确，A错误；系统竖直向上匀加速运动时，当a线拉力为15 N，由牛顿第二定律得，竖直方向有Fm·sin37°-mg=ma，水平方向有Fm·cos37°=Fb，解得Fb=12 N，此时加速度有最大值a=5 m/s2，故C正确；系统水平向右匀加速运动时，由牛顿第二定律得，竖直方向有Fa·sin37°=mg，水平方向有Fb-Fa·cos37°=ma，解得Fa=10 N，当Fb=15 N时，加速度最大为α≈11.7 m/s2，故D错误.

解题策略系统静止时，根据平衡条件即可求解绳子的拉力.当系统沿不同方向做匀加速直线运动时，绳子的拉力与加速度的大小和方向均有关.确定加速度的方向后，对物体进行受力分析，根据牛顿第二定律列有关绳子拉力的方程，当绳子拉力达到临界值时，加速度也达到临界值，计算出这个临界值即可[1].

2分离类临界问题

例2如图3所示，轻弹簧竖直固定在水平桌面上，质量为m1的木块放置在弹簧上但不拴接，质量为m2的铁块放置在木块上并通过跨过光滑定滑轮的轻质细线与质量为M的铁球连接，先用手托住铁球使细线恰好伸直但无张力，然后将铁球由静止释放.已知重力加速度为g，M>m2，轻弹簧劲度系数为k，弹簧始终处于弹性限度内，则（ ）.

A.铁球释放瞬间其加速度大小为M-m2M+m2g

B.铁块与木块分离之前细线的张力逐IOufDbLGP4Jz8L04mN+CKg==渐增大

C.铁块与木块分离时铁球的加速度大小为M-m2M+m2g

D.从初始状态到铁块与木块分离时，木块的位移为m2gk-m1（M-m2）g（M+m2）k

解析铁球释放瞬间，铁块与木块并未分离，所以三者加速度大小相同，开始时弹簧的弹力F=（m1+m2）g，设铁球释放瞬间其加速度大小为a，细线的张力为T，对于铁球有Mg-T=Ma，对于铁块与木块有T+F-（m1+m2）g=（m1+m2）a，联立解得a=MM+m1+m2g，故A错误；铁块与木块分离之前，结合上述可知，因弹簧的弹力逐渐减小，所以系统的加速度逐渐减小，则细线的张力逐渐增大，故B正确；铁块与木块分离时木块对铁块无作用力，所以对于铁块与铁球有Mg-m2g=（M+m2）a′，所以此时铁球的加速度大小为a′=M-m2M+m2g，故C正确；结合上述可知，初始状态弹簧的压缩量为x1=（m1+m2）gk，设铁块与木块分离瞬间弹簧的压缩量为x2，则对木块有kx2-m1g=m1a′，联立可得从初始状态到铁块与木块分离时木块的位移Δx=x1-x2=m2gk-m1（M-m2）g（M+m2）k，故D正确.

解题策略刚释放铁球M时，三者加速度大小相同，运用整体法和隔离法即可求出加速度；铁块与木块分离时，分离临界条件是木块对铁块无作用力，对铁块和铁球受力分析即可求出其分离时的加速度，根据弹簧的形变量即可求出铁块与木块分离时木块的位移大小.

3相对滑动的临界问题

例3如图4所示，质量为M=5 kg的一只长方体形空铁箱在水平拉力F作用下沿水平面向右匀加速运动，铁箱与水平面间的动摩擦因数μ1为0.3.这时铁箱内一个质量为m=1 kg的木块恰好能静止在后壁上.木块与铁箱内壁间的动摩擦因数μ2为0.25.设最大静摩擦力等于滑动摩擦力，g取10 m/s2.求：

（1）木块对铁箱压力的大小；

（2）水平拉力F的大小；

（3）减小拉力F，经过一段时间，木块沿铁箱左侧壁落到底部且不反弹，当箱的速度为6 m/s时撤去拉力，又经1 s时间木块从左侧到达右侧，则铁箱的长度是多少？

解析（1）木块恰好静止在铁箱的后壁上时，木块在竖直方向受力平衡有f=μ2FN=mg，

解得铁箱对木块的支持力的大小FN=40 N，根据牛顿第三定律，木块对铁箱压力的大小为40 N.

（2）木块在水平方向的加速度设为a，根据牛顿第二定律有FN=ma，以整体为研究对象，根据牛顿第二定律有F-μ1（m+M）g=（m+M）a，联立解得F=258 N.

（3）木块落到铁箱底部，撤去拉力后，铁箱和木块均以v=6 m/s的初速度做匀减速直线运动，铁箱受到地面的摩擦力f1=μ1（m+M）g=18 N，方向水平向左.铁箱受到木块的摩擦力f2=μ2mg=2.5 N，

方向水平向右.设铁箱的加速度大小为a1，根据牛顿第二定律有f1-f2=Ma1，解得a1=3.1 m/s2，方向水平向左.设木块的加速度大小为a2，根据牛顿第二定律有f2=μ2mg=ma2，解得a2=2.5 m/s2，方向水平向左，经过1 s，木块从铁箱的左侧到达右侧，则木块对地位移x2=vt-12a2t2，铁箱对地位移x1=vt-12a1t2，

故铁箱的长度为x=x1-x2=0.3 m.

解题策略两物体相接触且处于相对静止时，常存在着静摩擦力，静摩擦力达到最大值是发生相对滑动的临界条件.长方体形空铁箱在水平面上向右匀加速直线运动时，木块能恰好能静止在后壁上，说明木块在竖直方向向上的静摩擦力达到了最大值，也恰好与重力平衡，可求出木块对铁箱压力的大小和拉力F的大小[2].

4变力作用下的临界问题

例4某同学设计了一个测量风速大小的装置，装置如图5所示.初始时圆环被锁定，当风速的方向水平向右时，小球静止，该同学测得此时细线与竖直方向的夹角为θ=37°，已知圆环质量为2 kg，与杆的滑动摩擦因数为0.5.小球的质量m=4 kg，风对小球的作用力大小F=kv，其中k为比例系数，且k=2 kg/s，v为风速大小，g=10 m/s2.忽略细线质量、空气浮力和风对细线和圆环的作用力，且认为最大静摩擦等于滑动摩擦力.已知sin37°=0.6，cos37°=0.8.求：

（1）此时细线对小球的拉力的大小；

（2）解除圆环锁定，风速多大时，圆环恰不滑动；

（3）解除圆环锁定，若风速为18 m/s，稳定后小球和圆环保持相对静止，求此时小球的加速度.

解析（1）对小球受力分析知，小球受重力、风的作用力和线的拉力作用，则由平衡条件得

Tcosθ=mg，解得T=50 N.

（2）对小球和环组成的整体受力分析，由平衡条件得FN=（M+m）g=60 N，kv=μFN，解得v=15 m/s.

（3）由（2）可知，若风速为18 m/s，稳定后整体具有相同的加速度，所以对整体由牛顿第二定律得

kv′-f=（m+M）a，f=μFN，解得a=1 m/s2.

解题策略风力随风速的变化而变化，在变力作用下，圆环恰不滑动的临界条件是摩擦力达到最大静摩擦力，进而可以求解出此时的风速；当风速变化后，风力也发生变化，根据牛顿第二定律即可求解加速度[3].

5结束语

动力学临界问题的解决需要学生具备扎实的物理基础、敏锐的洞察力和灵活的解题思维.通过准确把握临界条件，运用合适的解题策略和数学工具，能够有效地解决这类复杂而具有挑战性的问题.动力学临界问题的解题策略是一个综合性的方法体系，需要学生在具体问题中不断探索和应用，以提高解题的准确性和效率.

参考文献：［1］

黄宽宽.动力学中的临界极值问题的解题策略[J].教学考试，2023（22）：43-48.

[2]倪华，陈传来，张井卫.动力学临界问题解题思路分析[J].中学教学参考，2020（35）：54-56.

[3]宋艳玲.高中物理动力学中隐蔽临界条件的挖掘对策[J].高考（综合版），2015（10）：222-223.

［责任编辑：李璟］