样本不均衡情况下的航空发动机轴承故障诊断方法

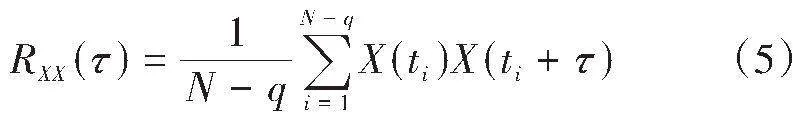
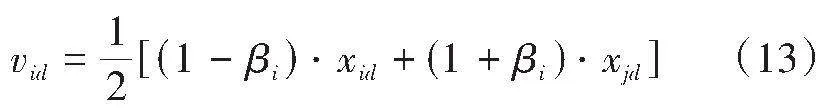
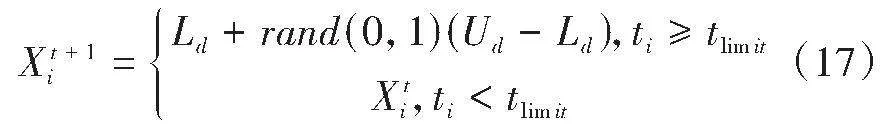
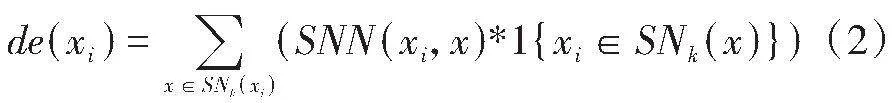
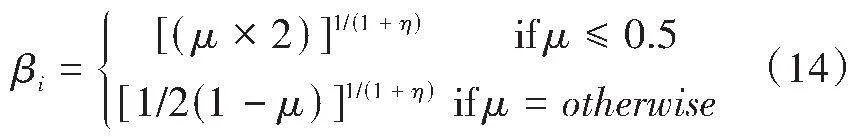
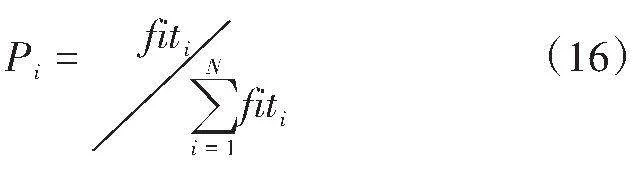
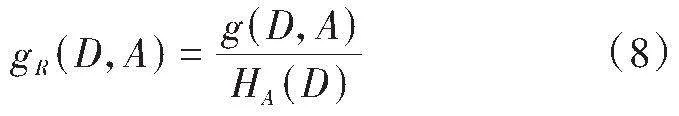
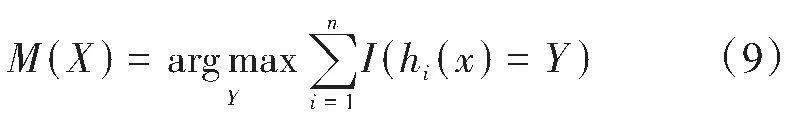
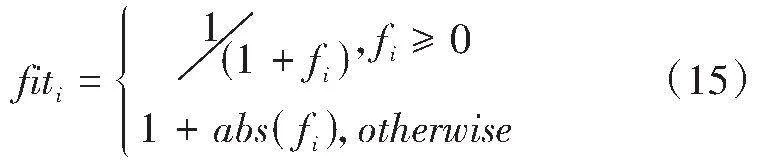
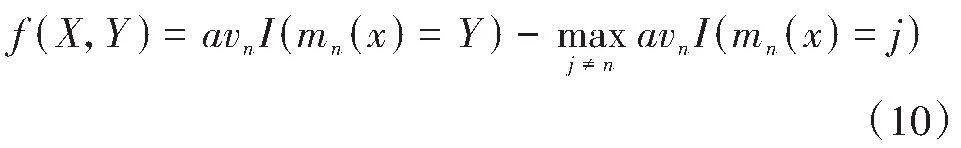
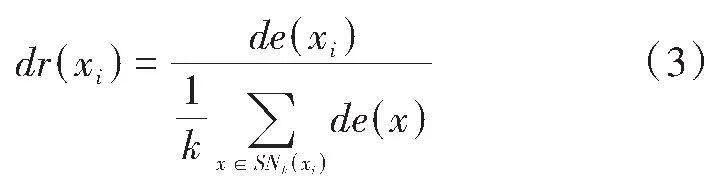
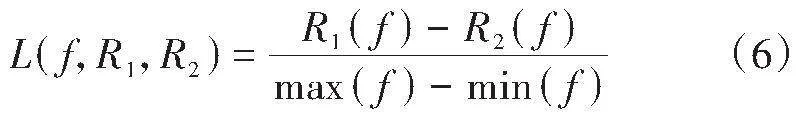
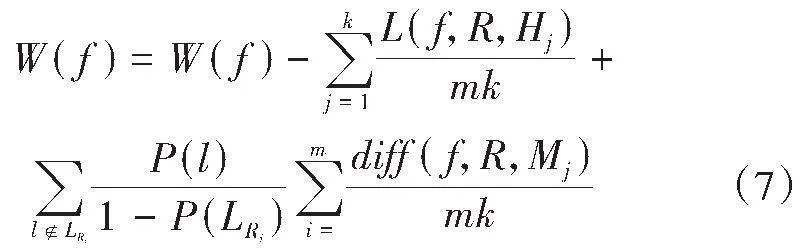
摘 要：航空发动机滚动轴承工作在高温、高压、高转速的恶劣环境下，故障率高，因此对于其故障的准确识别和判断尤为重要。但由于轴承故障的偶发性，各类故障样本不均衡的问题非常突出，大大影响了基于数据的模式识别方法的准确性。本文提出了一种样本不均衡条件下的航空发动机滚动轴承智能诊断方法，采用合成少数类过采样方法进行样本平衡，在完成时频域特征提取和特征选择之后，利用改进蜂群算法优化后的随机森林策略实现轴承故障分类，并在凯斯西储大学轴承数据集和实验室构建的模拟航空发动机滚动轴承数据集上进行了实验验证。结果显示在凯斯西储大学中度不均衡数据集下，故障识别的准确率为98.30%，在重度不均衡数据集下的分类结果为96.30%。在实验室构建的模拟航空发动机滚动轴承实验台上，不均衡数据集的分类结果为97.65%，重度不均衡数据集的分类准确率为95.67%。相关实验证明本文所提算法能够有效完成不均衡样本下的航空发动机滚动轴承故障诊断任务。

关键词：航空发动机轴承；故障诊断；数据不平衡；过采样；蜂群算法

中图分类号：TM931" " " " " " "文献标识码：A" " " " " "文章编号：1007 - 9734 （2024） 04 - 0005 - 07

0 引 言

滚动轴承作为航空发动机[1]的关键机械部件，工作在转速高、温度高、载荷大的恶劣环境当中，它的正常工作与否直接决定了飞机的飞行安全[2]。随着发动机推重比和功率的增加，对于滚动轴承这一发动机承力和传动部件的可靠性提出了更高的要求。实现航空发动机故障的预判，特别是主轴轴承的状态监测和故障诊断，如滚动体故障、轴承内圈故障、轴承外圈故障等[3][4]，对于降低飞机维修费用、减少飞行事故具有十分重要的意义。传统的基于统计学寿命模型和基于断裂力学方法的寿命模型已经被广泛应用[5]，而随着人工智能技术的发展，以支持向量机[6]、神经网络[7]为代表的基于物理属性变化的模式识别方法更是引起了研究人员的关注。

然而在实际场景中，由于故障的偶发性，轴承运行的监测数据中健康样本占据了大部分，而不同故障状态下的样本较少。为了解决数据不平衡的故障诊断问题，大多数研究通过数据增强方式对小样本进行数量补偿[8]。Zhang等[9]提出了一种基于生成式对抗网络的机械故障诊断方法，借助生成式对抗网络生成假样本来扩展可用数据集；Huang等[10]利用改进的带有辅助分类器的生成对抗网络生成多类型故障数据，有效解决标签错误、数据不均衡问题。但生成对抗网络对样本数量要求严苛，训练样本过多不符合发动机轴承故障实际，样本太少训练效果差。在此基础上，各种重采样方法被提出并应用。Ng等[11]人开发了一种基于多样化灵敏度的欠采样方法，从类别中选择信息样本，并将其应用于不平衡数据的分类任务。合成少数类过采样技术（Synthetic Minority Oversampling Technique， SMOTE）通过插值方法合成新样本，同样被应用于滚动轴承故障诊断当中[12]，但合成新样本时存在盲目性，易导致样本混叠，影响分类效果[13]。

在此基础上，针对数据不平衡条件下轴承故障的智能故障诊断方法，本文在传统SMOTE方法基础上，引入基于密度比的共享最近邻聚类算法（Density-ratio based Shared Nearest Neighbor cluster-ing， DRSNN），通过对少数类样本聚类生成保留结构的合成样本，并进一步利用蜂群算法优化传统随机森林分类的参数，以获取更好的分类效果，在此过程中为了有效提升蜂群算法的寻优精度和速度，引入模拟二进制交叉方法对观察蜂的寻优过程进行改进，从而实现对故障设备的准确识别。

1 相关原理

1.1" SMOTE-DRSNN

SMOTE通过对少数类样本进行人工插值来合成新样本并添加到数据集中，从而改善类别平衡，提高对少数类样本的识别能力。

为了进一步提升SMOTE策略生成样本的精度，在SMOTE中引入基于密度比的共享最近邻聚类算法，将利用SMOTE生成的初级样本带入其中，根据初级相似度，找到少数样本的k个最近邻，并进一步将式（1）（2）（3）计算得到的平均密度比与密度比阈值drT（一般为1）进行比较，确定是否保留。

其中SMOTE生成的样本xi和原始样本xj之间的共享最近邻近相似度（Shared Nearest Neighbour，SNN）的计算可通过式（1）完成：

[SNN（xi，xi）=Nk（xi）⋂Nj（xj）] （1）

计算新生成样本xi的密度为：

计算新生成样本的密度与其最邻近的平均密度之比为：

1.2" 降阶变分模态分解

变分模态分解（Variational mode decomposition， VMD）[14]是一种自适应、完全非递归的模态变分和信号处理方法。它能够根据不同情况确定所给序列的模态分解个数，并自适应地匹配每种模态的最佳中心频率和有限带宽，实现固有模态分量（IMF）的有效分离、信号的频域划分，进而得到给定信号的有效分解成分，最终获得变分问题的最优解。但VMD对瞬态信息不敏感，从原始信号中提取瞬态的信息难度较大。

本文使用降阶变分模态分解（Reduced-Order Variational Mode Decomposition，RVMD）[15]以获取更多维度的信号。它是一种数据驱动的模态分解方法，通过VMD操作将原始信号的低频模态分解为两个模态，直到被VMD分离的两个模态在中心频率上足够接近，其停止准则定义为：

[fd=（fh-fl）/fl] （4）

其中fl和fh分别对应低频模式Ul（t）和高频模式Uh（t）的中心频率。如果fd大于精确阈值，则达到停止准则，即原始信号Ui（t） = Ul（t）+ Uh（t）。由于滚动轴承的振动信号具有较高的二阶循环平稳性，本文模态的选择依据是各模态包络的无偏自相关性，其计算公式如下：

其中X是每个模式的包络，τ=q/fs表示延迟因子，q=0，1，…，N-1。

1.3" Relief-F特征选择

Relief-F算法是一种特征子集选择方法，它根据每个特征与类别的相关性为每个特征赋予不同的权重，并对低于一定阈值的特征权重进行去除[16]。Relief-F算法可以计算特征f上两个对象R1和R2之间的距离：

其中R1（f）表示R1在特征f上的值，R2（f）表示R2在特征f上的值，max（f）和min（f）分别表示特征f上的最大值和最小值。然后更新每个特征的权重：

其中Hj和Mj分别表示对象R和已知对象的第j个邻居，L（f，R，Mj）和L（f，R，Mj）分别表示对象R和Hj、R和Mj之间的距离，m为算法迭代次数，k为相邻对象的个数，[LRi]为对象Ri的标签，P（L[Ri]）是对象Ri属于标签的概率，P（L）代表标签L的概率。

1.4" 随机森林

随机森林是由一组决策树基分类器组成的分类器[17]，采用bagging方法从原始样本随机地选择样本来训练分类器，解决了单一分类器精度低和过拟合的问题。

实现随机森林分类的主要过程如下：

（1）对原始特征矩阵进行自动抽样，生成新的子特征集。

（2）对每个子特征集进行训练，得到决策树。在此过程中需要借助公式（8）和信息熵g（D，A）、经验熵HA（D），求取信息增益率比gR（D，A），并利用最大的增益率作为节点，递归得到子节点。

（3）所有的决策树构成一个“森林”，每一个决策树模型得到样本的分类结果，根据分类结果对每个样本进行投票，并最终确定结果。

其中I（*）是线性函数，hi（x）表示其中一个决策树的回归预测值，每一个决策树分类模型的训练集从原始数据（X，Y）抽样得到。利用残差函数f（X，Y）求解正确分类大于错误分类的具体情况，其公式如下：

由此可知，f（X，Y）和分类预测结果密切相关，f（X，Y）越大结果越准确。

1.5" 改进人工蜂群算法

对于上述的随机森林策略，其参数的选择，如抽取的特征、生成树的数量等，直接决定其分类精度和效率。为了获得最优参数，引入人工蜂群算法（Arti-ficial Bee Colony，ABC）对其进行优化选择。该方法是一种模拟蜜蜂采蜜过程的群智能算法，考虑其经常遭遇的容易陷入局部最优的情况[18]，在观察蜂阶段利用模拟二进制交叉方法（Simulated binary crossover，SBX），将其与初始蜜源结合，产生新的蜜源，有效地提升了算法跳出局部最优解的能力。

ABC算法在求解优化问题时，蜜源的位置代表问题的潜在解。蜜源i（i=1，2，…，S）的质量对应解fi的适应度值。设问题求解的维数为D，蜜源i在搜索空间中随机生成的初始位置可以表示为：

[xid=Ld+rand（0，1）（Ud-Ld）] （11）

其中Ld和Ud分别表示搜索空间的上下限，d=1，2，…，D。

在采蜜蜂阶段，一个新的蜜源vid是利用式（12）在蜜源xid周围搜索产生：

[vid=xid+φ（xid-xjd）] （12）

式（12）中φ为均匀分布的随机数，j∈{1，2，…，S}，且j≠i。

观察蜂阶段，为了增加观察蜂的寻优能力以及跳出局部最优的能力，使用模拟交叉二进制算法优化蜜源。模拟交叉二进制算法公式为：

其中，β是一个随机数。

其中，μ是属于（0，1）的随机数，η是交叉指数，β值接近1。生成解的质量可以通过如式（15）所示的适应度来评估：

其中fi为解的函数值。

采蜜蜂跟随的概率Pi为：

在搜索过程中，如果蜜源Xi在ti迭代后达到阈值tlimit且没有找到更好的蜜源，则放弃该蜜源，并将其对应的采蜜蜂角色改为侦察蜂，将该蜜源更新为：

2 故障诊断算法框架

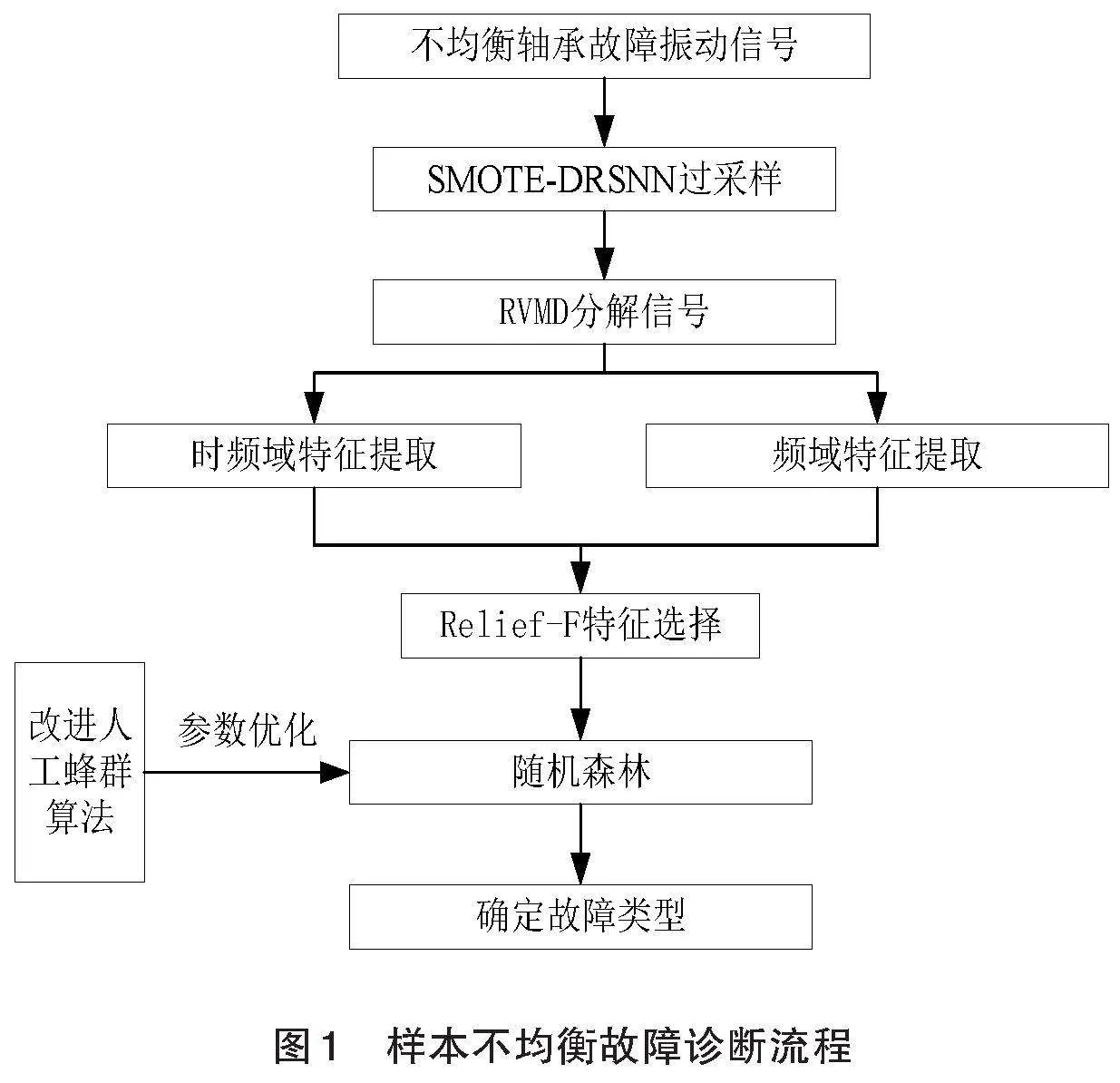
针对样本不均衡条件下的航空轴承智能诊断，本文通过SMOTE-DRSNN对少量故障样本进行过采样，解决样本类间不均衡问题，并利用RVMD分解构建多个维度的信号，进而完成时频域特征提取。随后利用改进的人工蜂群算法优化随机森林相关参数，并利用优化后的随机森林分类器实现故障模式识别。具体步骤如图1所示：

（1）SMOTE-DRSNN过采样。对不均衡数据集中少数样本进行过采样，平衡数据集中的各个样本比例。

（2）RVMD分解。获得各个信号不同模式下的多个频段信号，供后续特征提取。

（3）时频域特征提取。对分解后的信号求取其峭度、方根幅值、峰峰值等，实现时频域特征提取，得到每个样本的多个维度特征。

（4）Relief-F特征选择。对多维度特征进行特征权重的排序，保留权重值较大的特征。

（5）优化的随机森林模型。利用蜂群算法寻优随机森林分类器的参数以提高其分类能力，并在观察蜂阶段引入模拟二进制交叉方法来提高蜂群算法的寻优能力。

（6）识别故障类型。利用优化后的随机森林模型识别不同故障模式。

3 实验验证

为了验证所提出方法在航空发动机轴承故障诊断当中的有效性，本文将相关算法在凯斯西储大学轴承数据集和团队自主构建的航空发动机主轴轴承故障模拟实验台中进行了实验验证。

3.1" 数据集描述

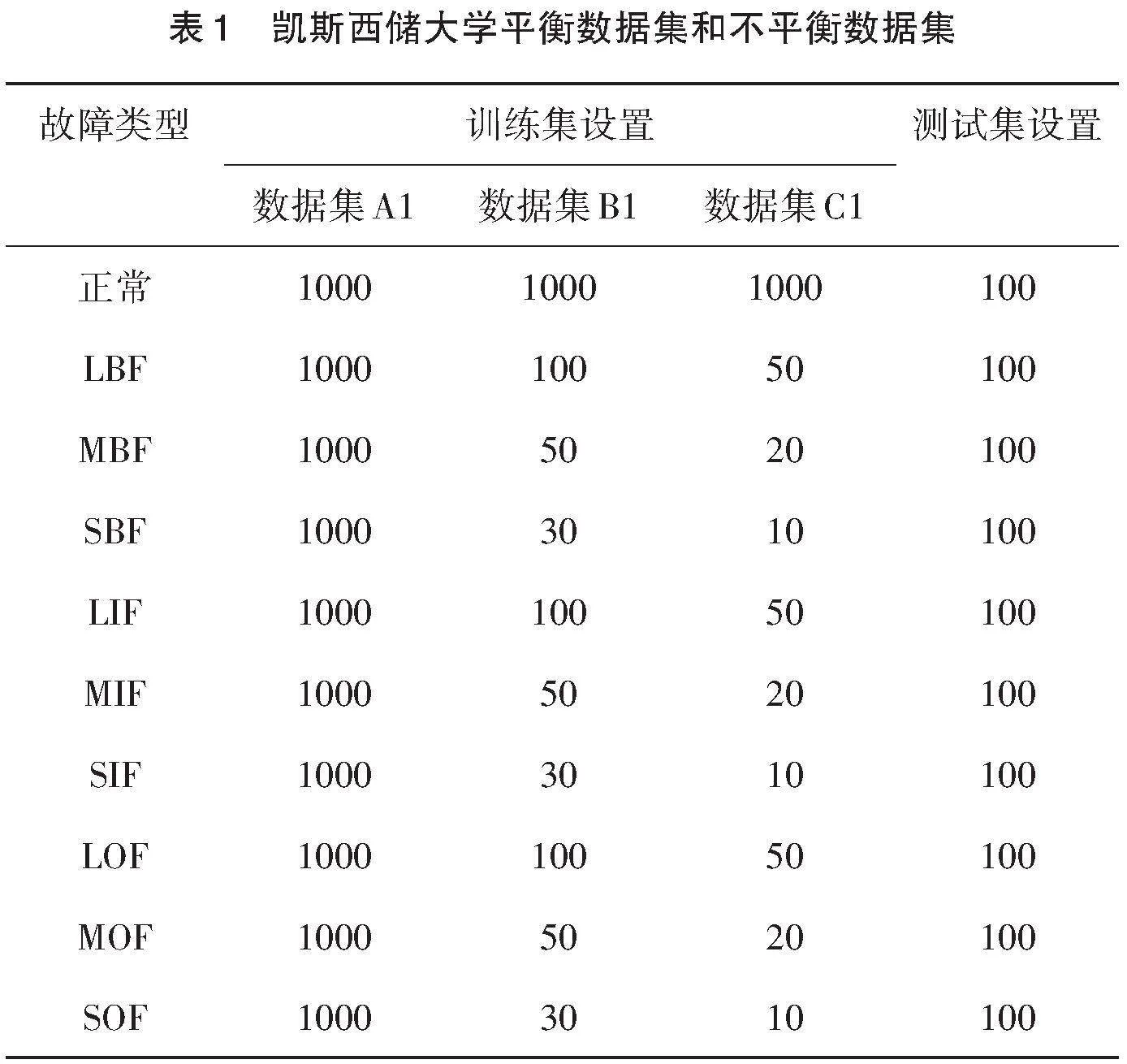
凯斯西储大学轴承数据集[19]包含了轴承的10种运行状态：正常、轻度滚动体故障（LBF）、中度滚动体故障（MBF）、严重滚动体故障（SBF）、轻内故障（LIF）、中内故障（MIF）、严重内故障（SIF）、轻外故障（LOF）、中外故障（MOF）、严重外故障（SOF）。所有数据按照48Khz的采样频率采集自直径为0.007英寸、0.014英寸、0.028英寸轴承的轻度、中度、重度三个层次故障。

采集的故障数据情况如表1所示，其中数据集A1中每类故障数据有1000个样本，是典型的平衡数据集。为了更真实地模拟现实中存在的数据不平衡情况，数据集B1中轻度故障、中度故障和严重故障的训练样本数分别减少到100个、50个和30个。进一步减少错误样本的数量构建数据集C1，其中轻度故障50个样本，中度故障20个样本，严重故障10个样本。

图2是构建的模拟航空发动机滚动轴承的实验台，系统中利用三相异步驱动电机带动轴承转动，其中电机额定功率1500W，最高转速6000rpm，定子槽数36个，转子条数28个，采集故障信号的两个加速度传感器分别位于轴承座左侧的垂直方向和水平方向。本文采集的轴承数据对应的转速是200r/min，采样频率48kHz，通过定长滑动窗口在每个故障模式下获得4000个样本。

故障类型包括轴承保持架故障、滚动球故障（0.5mm孔）、内圈故障（直径1mm）、外圈故障（直径1mm）、内圈和外圈同时故障5种（见图3）。

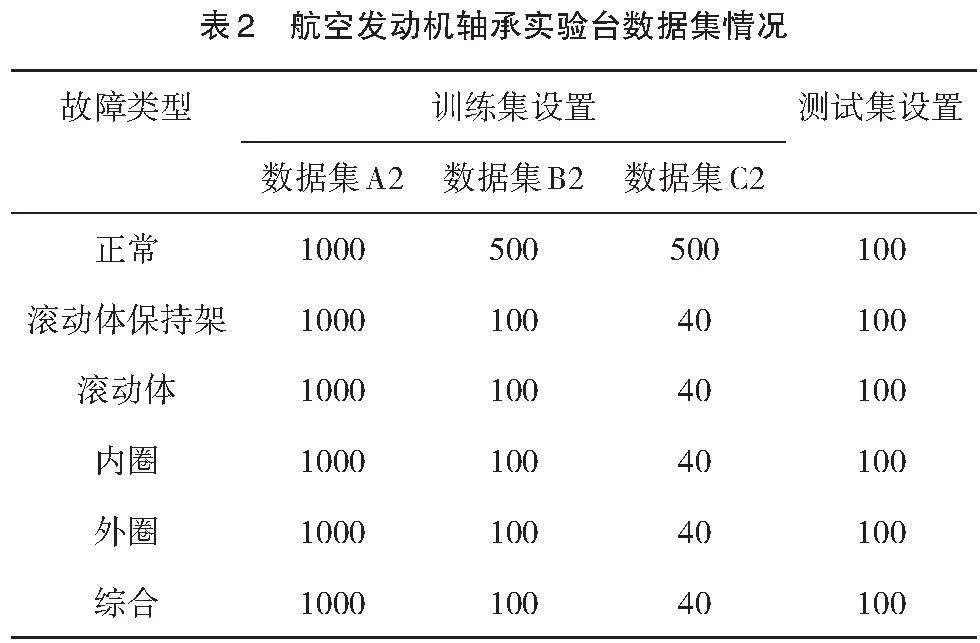
采集的故障数据集情况如表2所示，数据集A2包含每类故障的1000个样本作为平衡数据集，不平衡数据集B2中的故障样本数量减少到100个，数据集C2进一步加剧了数据不平衡程度，故障样本的数量减少到40个。

3.2" 实验结果分析

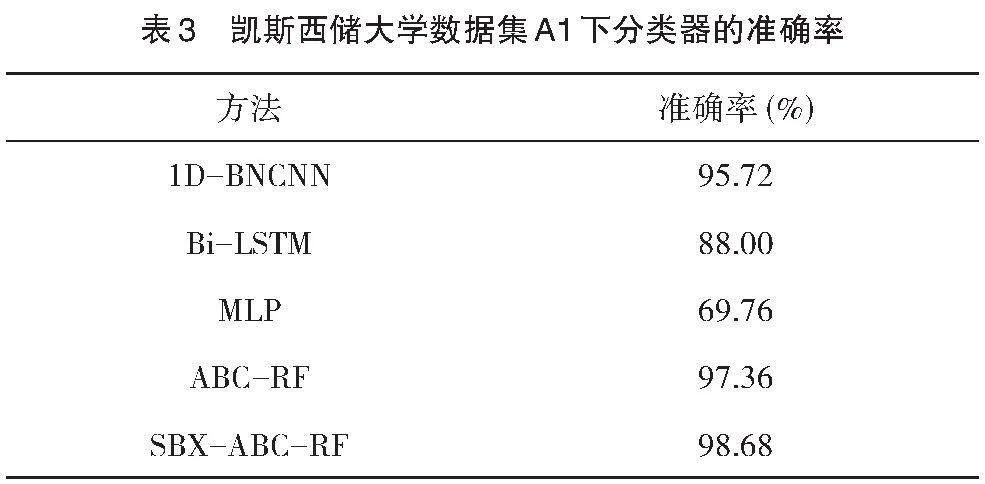
相关算法首先在凯斯西储大学数据集上进行验证，并与1D-BNCNN、LSTM、MLP[20]等方法的结果进行对比。在均衡故障数据集下的分类结果如表3所示。可以看出本文提出的改进的SBX-ABC-RF方法分类准确率最高，达到98.68%。相比未加改进的ABC-RF算法准确率提升了0.72%。

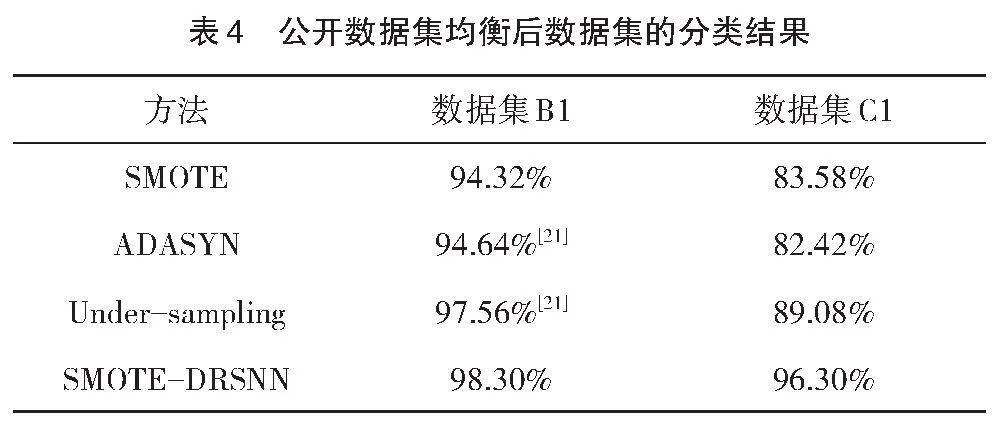
进一步在不均衡数据集上进行测试，引入SMOTE-DRSNN过采样方法，与传统的SMOTE、ADASYN、Under-sampling[21]三种采样方法进行对比，这些方法都采用优化后随机森林策略进行分类，其结果如表4所示。结果表明不管是B1还是不均衡程度更甚的C1数据集，本文提出的SMOTE-DRSNN过采样方法，相比于其他三种方法拥有更高的准确性，特别是应对C1数据集的故障诊断问题时，本文所提出方法的准确率相比传统方法，提升了13.88%。

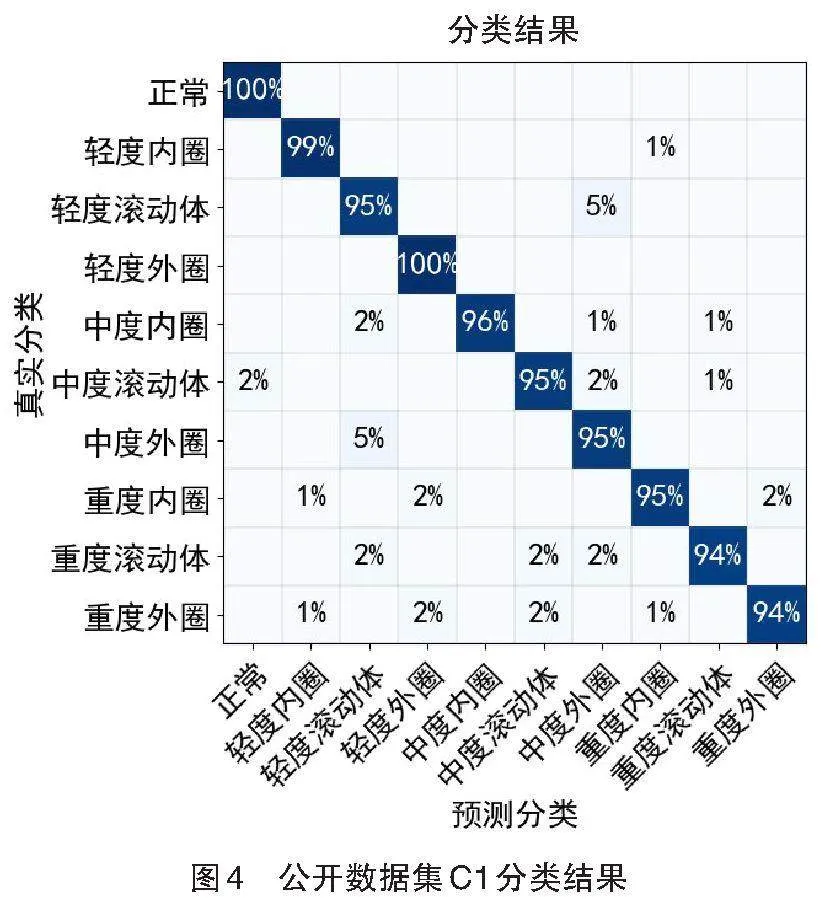
图4展示了本文所提方法在公开数据集C1中的分类结果，使用SMOTE-DRSNN方法对不公平数据集C1处理后，有效解决了样本不均衡问题，模型的分类准确率达到96.30%。

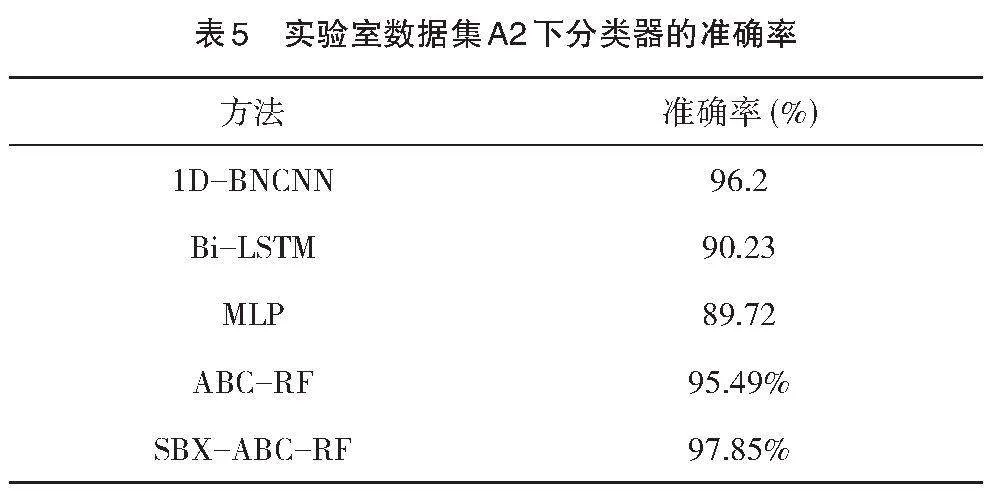
更进一步，将本文所提方法在航空发动机滚动轴承模拟实验室上进行测试，在数据集均衡条件下的分类结果如表5。显然，本文所提方法在数据集A2的分类准确率达到97.85%，最多高于其他方法8.13%。

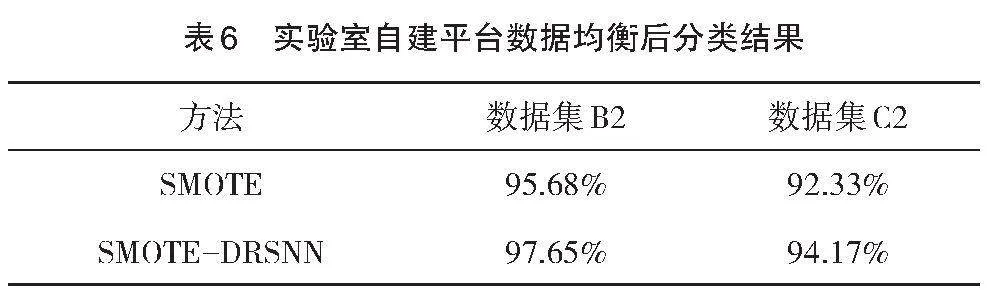
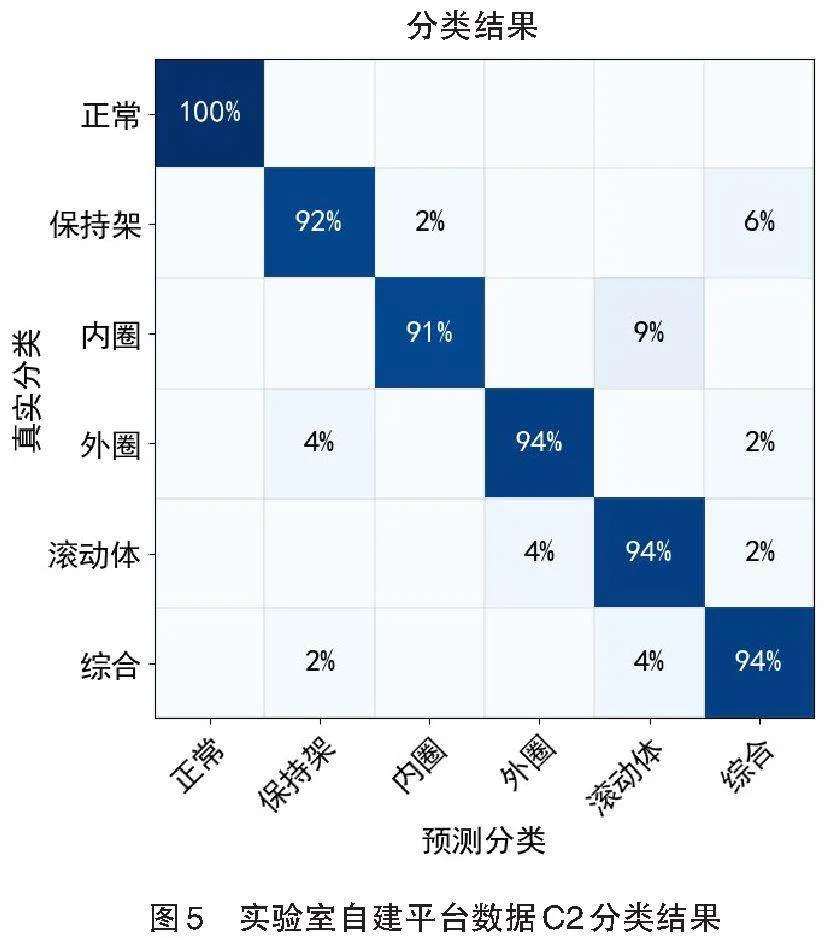
同样将该方法在不平衡数据集B2、C2下进行了验证，结果如表6所示，相比于其他方法，本文提出的方法在实验室数据集B2中的分类准确率能够达到97.65%。随着数据不平衡性的增加，故障样本的数量减少导致故障信息缺失，C2数据集的分类准确率有所下降，但仍然高于传统方法。图5展示了本文所提方法在数据集C2上分类对应的结果，说明本文所提方法具有较明显的优势。

4 结 论

本文针对数据不均衡情况下的航空发动机滚动轴承故障诊断问题进行了研究，通过引入SMOTE-DRSNN算法实现故障数据类均衡，并借助改进蜂群算法优化随机森林策略，实现故障模式识别。设计的算法分别在CWRU数据集和实验室轴承故障诊断实验台上进行验证，两个平台下不均衡轴承故障数据的分类结果最高达到97.85%，能够满足旋转机械轴承故障诊断的准确性、鲁棒性要求。下一步将把相关算法在真实航空发动机平台上进行测试。

参考文献：

［1］高文君，吕亚国，刘振侠.航空发动机主轴轴承应用技术［M］.北京：科学出版社，2021.

［2］KANG Y X，CHEN G，WANG H，et al.Fault anomaly detection method of aero-engine rolling bearing based on distillation learning［J］.ISA Transactions，2023，145：387-398.

［3］YU A，HUANG H Z，LI H，et al.Reliability analysis of rolling bearings considering internal clearance ［J］.Journal of Mechanical Science Technology，2020，34：3963–3971.

［4］ZHU T F，LUO C，ZHANG Z H，et al.Minority oversampling for imbalanced time series classi-fication［J］.Knowledge-Based Systems，2022，247：108764.

［5］苗学问，等.基于支持向量机的滚动轴承状态寿命模型［J］.航空动力学报，2008，23（12）：2190-2196.

［6］刘海瑞，武宪威，李鹏，等.基于APSO-LSSVM的航空发动机轴承故障诊断及寿命预测［J］.测控技术，2023（9）：1-7.

［7］卓识，战利伟，白晓峰，等.基于CWT-AT-CNN的航空滚动轴承故障诊断方法［J］.轴承，2023（12）：1-9.

［8］韩淞宇，邵海东，姜洪开，等.基于提升卷积神经网络的航空发动机高速轴承智能故障诊断［J］.航空学报，2022，43（9）：625479.

［9］ZHANG W，LI X，JIA X D，et al.Machinery fault diagnosis with imbalanced data using deep generative adversarial net-works［J］.Measurement，2020，152：107377.

［10］HUANG N，CHEN Q，CAI G.Fault diagnosis of bearing in wind turbine gearbox under actual operating conditions driven by limited data with noise labels［J］.IEEE Trans-actions on Instrument and Measurement，2021，70（1）：1-10.

［11］NG W W Y，HU J，YEUNG D S，et al.Diversified sensitivity-based undersampling for Imbalance Classifica-tion problems［J］.IEEE Transactions on Cybernetics，2017，45（11）：2402–2412.

[12]余松，胡东，唐超，等.基于TLR-ADASYN平衡化数据集的MSSA-SVM变压器故障诊断[J].高电压技术，2021，47（11）：3845-3853.

[13]黄海松，魏建安，任竹鹏，等.基于失衡样本特性过采样算法与SVM的滚动轴承故障诊断[J].振动与冲击，2020，39（10）：65-74.

[14]WU Y J，HU Z Z，AN W L，et al. Automatic diagnosis of rolling element bearing under different conditions based on RVMD and envelop order capture[J].IEEE ACCESS，2019（7）：91799-91808.

[15]LIAO Z-M，ZHAO Z，CHEN L-B，et al.Reduced-order variational mode decomposition to reveal transient and non-stationary dynamics in fluid flows[J].Journal of Fluid Mechanics，2023，966：A7.

[16]孙林，杜雯娟，李硕，等.基于标记相关性和Relief-F的多标记特征选择[J].西北大学学报，2022，52（5）：834-846.

[17]CHEN S Z，YANG R，ZHONG M Y.Graph-based semi-supervised random forest for rotating machinery gearbox [J].Control Engineering Practice，2021，117：104952.

[18]秦全德，程适，李丽，等.人工蜂群算法研究综述[J].智能系统学报，2014，9（2）：127-135.

[19]WANG Z， ZHANG Q， XIONG J，et al.Fault diagnosis of a rolling bearing using wavelet packet denoising and random forests[J].IEEE Sensors Journal，2017，17（17）：5581–5588.

[20]YUAN L， LIAN D， KANG X， et al. Rolling bearing fault diagnosis based on convolutional neural network and support vector machine[J].Institute of Electrical and Electronics Engineers Access，2020（8）：137395-137406.

[21]ZHAO B，ZHANG X M，LI H，et al.Intelligent fault diagnosis of rolling bearings based on normalized CNN considering data imbalance and variable working conditions[J].Knowledge-Based Systems，2020，199：105971.

Research on Fault Diagnosis Strategy for Aeroengine Bearing

with Imbalanced Data

Abstract：The mechanical rolling bearing of aeroengine always works in poor environment with long running time and high load，which causes high failure rate and threatens the safety of people’s live，so it is important to early detect the faults of rolling bearings.But as the faults occurred randomly， the fault data is unbalanced，and the accuracy of fault detection with pattern recognition strategy will be affected.To solve this problem，an intelligent diagnosis method for aeroengine rolling bearing with unbalanced samples is proposed in this paper.Firstly，the reduced-order variational mode decomposition is used to balance the fault data， and random forest algorithm is introduced to recognize the faults，and in order to improve the detection accuracy，an improved artificial bee colony algorithm is proposed to optimize the random forest strategy.Finally，the proposed strategy is verified on the Case Western Reserve University bearing dataset and the platform constructed by our laboratory.The accuracy is 98.30% in the moderately imbalanced dataset of Case Western Reserve University，and the classification result is 96.30% in the severely imbalanced dataset.With the platform in our laboratory，the classification result for moderate imbalanced data set is 97.65%，and the classification accuracy for severely imbalanced data set is 95.67%.

Key words：aeroengine bearing;fault diagnosis;imbalanced data;oversampling;artificial bee colony algorithm