座位与成绩的邻近效应研究

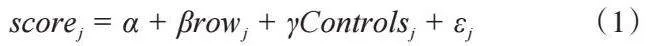
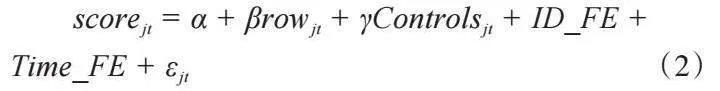
摘 要：基于随机控制试验方法，本文通过对4个班级210名学生2个多月时间的试验检验了座位是否能够影响学生学习成绩。结果表明，前排学生比相邻后排学生的百分位成绩平均提升4.5个百分点，即座位和成绩之间存在邻近效应。研究结论能给“往前坐”的学风建设政策提供实证支撑，对于推进校园学风建设具有现实意义。

关键词：座位；成绩；邻近效应；随机控制试验

一、引言

“往前坐”往往是老师上课对学生座位的一般要求，这通常是基于一种默认的共识，即前排座位有利于学习。因为通常认为坐在前排的同学拥有靠得近、听得清、看得明的客观优势，可以得到更好的授课体验，进而有利于学习成绩提升，该效应称为邻近效应。但在教学的过程中，我们同样会发现一种现象：认真学习的同学坐在哪里都会认真学习，无心学习的同学坐在哪里照样心猿意马，体现出一种与座位无关的学习主观性。因此，“往前坐”是“确有其效”还是老师的“一厢情愿”？这是一个有趣而值得探讨的问题。若“往前坐”确有其效，那么前排座位是一种微观层面的优质稀缺资源，应该得到有效且公平地利用，可以通过随机分配的方式进行座位安排；若“往前坐”仅是老师的“一厢情愿”，那么这便只是一种课堂展现形式，无关乎成绩，需对“往前坐”的意义进行反思。

对邻近效应的探讨历时已久，但结论尚存争议。Griffith最早从心理学的角度开展相关研究，得出坐在中间排的同学比前后排的同学成绩更高的非典型结论[1]。后续学者研究中有表明邻近效应存在的，Benedict和Hoag发现选择坐在教室前面的学生表现更好，当喜欢后座的学生座位向前移动时，这些学生的成绩有所提高[2]；Perkins和Wieman研究了一个有201名学生的大型物理教室，这些学生在上半学期被随机分配座位，然后在下半学期被要求交换座位（从前到后），发现这对上半学期的成绩分布产生了重大影响，后排的学生获得F的可能性比前排的学生高出近六倍[3]；此外，一些研究同样表明了邻近效应的存在[4～5]。相应的，有学者研究不支持邻近效应[6～7]，对此一个可能的解释是邻近效应受教室大小影响，对于大教室上课的学生，座位越往前越能提升成绩，而这种现象在小教室不存在[8]。国内学者对邻近效应的研究较少，有学者通过记录学生自主选座数据，采用控制变量回归的方法来推导因果关系，表明座位越靠前，学习成绩越好 [9]；采用问卷调查法和单因素方差分析进行因果分析，表明学生在自由选择课堂座位时，会形成以教师为中心的“学业优胜区” [10]。

尽管当前有较多相关研究，但现有研究主要存在因果推导的可靠性不足的问题，如采用控制变量的回归分析和v/OiSxfHss4J8550sJJGclDcYEB9TCwQYWFRRzjPOg0=单因素方差分析都没有本质上解决内生性问题，无法从相关关系有效地推导到因果关系，即有可能是好学生选择了前排的位置，而不是前排位置造就了好学生。推导因果关系的主要的困难在于如何内生性问题，而解决内生性最有效的办法是随机控制试验（Randomized Control Trials ，RCT） [11]。

鉴于此，本文采用RCT方法进行座位与成绩之间的因果推断。具体的，每堂课对学生上课的座位进行随机分配，并记录座位，同时每堂课进行课后测试，记录成绩，试验持续了2个多月时间。通过RCT确保作为核心解释变量的座位最大程度上符合条件独立假设（Conditional Independence Assumption，CIA），使得座位与成绩之间的因果关系推导具备可靠性，这亦是本文的主要边际贡献。

二、试验设计

本试验开始于2023年秋季学期初，至2023年11月中旬结束，共2个多月时间。以温州商学院金融贸易学院《金融市场与金融机构》课程的本科学生为研究对象，共4个班，210名学生参与了研究。

在试验开始的第1周，我们收集到了学生的基本情况，包括性别、学号、手机号、期初平均绩点、座位倾向等信息。同时根据上课教室结构，利用EXCEL制作随机座位程序，可以实现一键随机安排全班同学座位。正式试验从第2周开始，课前我们通过随机座位程序生成座位分布，提前发布在微信群，学生上课根据座位入座。每堂课结束前5分钟左右，我们会安排一次随堂测试，测试内容均来自本节课的授课内容，一般由10～12题客观题构成，测试通过手机上的“课堂派”平台发布，为了给学生多一点空间和乐趣，我们设置了每次测试有2次切屏的机会，但同时，由于题目均为原创题目，网络上一般找不到原题，通过这样的方式来最大限度保证随堂测试能反映出学生的真实所学。

三、数据与计量模型

（一）变量说明

试验期内，因节假日等因素影响，4个班完成了7周次试验，累计获得了210名学生1271个试验数据。在试验过程中，少部分同学存在随意测试、误交作业的情况，为此，本文对测试成绩尾部5%的数据进行了缩尾处理。相关变量定义如下：row（座位），前排（1～2排）、中排（3～4排）、后排（5排及以后）分别计1、2、3；score（课堂测试成绩），随堂测试结果，每次总分为10～13分，classroom（上课教室），共涉及两个教室，分别取0、1；gender（性别），男性0，女性1；grade（年级），大四0，大二1。pref-seat（座位偏好），通过问卷获得学生座位倾向，前排（1～2排）、中排（3～4排）、后排（5排及以后）分别计1、2、3；GPA（平均绩点），期初平均学分绩点。

（二）随机性检验

座位的随机性是本文的核心，试验的随机性直接决定了本文试验结果的可靠性，因此在数据分析之前，我们首先必须对随机性进行检验。因为本文的座位分为前、中、后三个分组变量，t检验不再适用，所以采用单因素方差分析（One-way ANOVA）进行随机性检验。具体的，选取学生的学号、平均绩点（GPA）、手机号码、座位倾向（pref-seat）和性别（gender）5个变量进行方差分析，分析这5个变量在前、中、后三个区域中的均值是否存在显著差异，若是真实随机，则不应该存在显著的组间差异。在7次试验35个指标中，有33个ANOVA P值是大于 0.1的（限于篇幅未列出结果，有需要的读者可向作者索要，下同），表明这些变量不存在显著的组件差异。同时，Bartlett's P值均大于 0.1，通过方差齐性检验。因此，本文的座位安排是满足随机性要求的，基于该数据的因果推断是可靠的。

（三）模型设定

本文基础实证模型采用横截面数据回归模型，因为核心解释变量作为随机变量，已经满足条件独立假设（CIA），内生性的问题已经大大削弱，基础模型设定如下：

其中scorej、rowj分别表示学生j的测试成绩和座位区域，Controlsj表示相关控制变量，包括上课教室、性别、年级、平均学分绩点等。需要说明的是，一般情况下，在回归方程中加入控制变量起到两个作用，一是保证条件均值假设CIA成立，二是减小误差，提高估计精度。本文核心变量[rowj]作为随机变量，具备外生性，与[εj]本身不相关，这已经保证了OLS估计量的一致性，因此从内生性的角度出发，此时加入控制变量并无作用。但从估计精度的角度看，还是很有必要，因为座位毕竟提供的信息太少，估计精度不高。所有回归均采用稳健标准误差。模型中的[β]是研究关注的重点，若存在邻近效应，则[β]应显著为负。

四、实证结果

（一）基础回归结果

首先，基础回归模型中不加入控制变量，图1展示了回归结果，7次回归结果的[β]系数都是负数，但只有3次是在10%的水平上显著，部分支持了邻近效应。以第1周次结果为例，row每增加1单位（即中排比前排、后排比中排），平均成绩下降0.435分，而第一次测试成绩score的平均值为6.01，标准差为2.01，因此座位每往后1区域，平均测试成绩下降7.2%（0.435/6.01）。相应的，根据第2～7周次回归结果，座位每往后1区域，平均成绩分别下降4.23%、5.33%、1.3%、0%、2.65%、4.6%。相应的可以计算，row每增加一个标准差，第1～7周次score分别降低0.21、0.12、0.12、0.04、0.04、0.09、0.17个标准差，体现出座位差异能解释4%～21%的成绩差异。整体上表明邻近效应的存在，尽管有些周次的回归结果不显著，一个可能原因是基础回归中没加入控制变量，导致估计精度不够。

在基础回归模型的基础上，我们加入了年级、教室、性别、平均绩点四个控制变量。在控制了这些因素后，row的系数基本没有发生大的变化，相关结果分析不再赘述，row的7个系数中有4个在10% 的水平上显著，拟合度均提高到10%左右。在控制变量中，最显著的影响是平均绩点GPA，表明平时成绩好的同学，上课测试成绩也会好，平均绩点能解释成绩20%～45%的差异。

（二）面板数据回归结果

如前所述，尽管座位是随机变量满足CIA，可以解决内生性问题，横截面数据模型的估计值是一致的，但同时，横截面模型的估计效率不高，尽管加入了一些控制变量。而面板数据的固定效应模型可以对不可观测的非时变因素进行控制，提高估计精度。鉴于此，本文将横截面数据构造成面板数据，采用面板数据模型（2）进行回归。

需要说明的是：一是模型中的控制变量如年级、性别等均是非时变变量，均已包含在ID的固定效应中（ID_FE）；二是为了使得成绩能够跨期比较，我们对成绩进行了百分位处理，即先将每一期成绩进行排序，再除以当期试验的总人数，得到百分位成绩scoreperc，该值越小表明成绩越好。根据固定效应回归结果，座位指标row在1% 的水平上显著，row每增加1（即每往后挪一个区域），百分位成绩往后挪4.5个百分点，表明存在邻近效应。从拟合度上看，调整后R2达到 31%，显著高于横截面回归模型，验证了面板模型的高效性。

（三）采用座位虚拟变量的回归结果

此外，我们引入座位虚拟变量来衡量位置，座位虚拟变量可以提高邻近效应的分析颗粒度。具体的，为避免共线性引入dum2-dum7共6个虚拟变量，分别代表第2排-第7排座位（因第7排之后样本较少，所以将第7排及之后的统一纳入第7排），虚拟变量的回归系数代表相应座位与第一排座位邻近效应的差距，采用面板数据模型（3）进行回归。

图2展示了回归结果，整体上看，越往后的位置，其百分位成绩也越靠后，支持了前文的观点。需要说明的是，第2和3排的回归系数不显著，意味着第2排、3排位置与第1排没有显著差别，表明位置的作用存在一定的阈值效应。

五、结论

本文采用随机控制试验方法，通过对4个班级210名学生2个多月时间的试验检验了“往前坐”是否能够提升学生学习成绩。研究表明，前排座位能显著提升学生成绩，即存在邻近效应，学生座位每往前一个区域（座位分前中后三个区域），百分位成绩提升4.5个百分点。且邻近效应在学习意愿和性别方面没有异质性。

本文采用的随机控制试验能够可靠地推导座位与成绩的因果关系，弥补了当前相关研究的不足。同时研究结果能给“往前坐”的学风建设政策提供实证支撑。

进一步讨论：本文结论支持了邻近效应的存在，一个直接的政策建议就是鼓励“往前坐”。但在教学实践中，可能会存在两种情况：一是前排会空着，导致这个优质的稀缺资源被浪费；二是学生抢着前排坐，导致前排资源不能公平分配。如何将前排高效且公平用起来是教学需要认真考虑的事情。在本次试验过程中采用的随机座位模式或许可以提供一些思路。在这个试验过程中，随机排座体现出了一些好处：前排座位根据随机安排，都会有人坐，不会存在资源浪费，保证了资源的有效利用；随机安排使得大家都有相同概率能够获得前排优质资源，实现微观层面的教育公平；通过随机方式，打散了学生的群聚效应，课堂纪律相比自由选择更容易管理；通过座位安排，可以清晰掌握每个学生的位置，对于课堂提问和点名有显著的帮助。因此，随机座位安排可以高效、公平地利用前排资源，同时对于课堂纪律管理具有较好的作用。

参考文献：

[1] GRIFFITH C.R.A Comment Upon the Psychology of the Audience[J].Psychological Monographs，1921，30（3）：36-47.

[2] BENEDICT M E，HOAG J.Seating Location in Large Lectures：Are Seating Preferences or Location Related to Course Performance？ [J].The Journal of Economic Education， 2004，35（3）：215-231.

[3] PERKINS K K，WIEMAN C E.The Surprising Impact of Seat Location on Student Performance[J]. The Physics Teacher，2005，43（1）：30-33.

[4] ARMSTRONG N，CHANG S M. Location，Location，Location[J]. Journal of College Science Teaching，2007，37（2）：54-58.

[5] ZOMORODIAN K，PARVA M，AHRARI I，TAVANA S，HEMYARI C，PAKSHRI K，SAHRAIAN A.The Effect of Seating Preferences of the Medical Students on Educational Achievement[J]. Medical Educa_{x7AxLuHjm+yhAjsZ1uIlLlL2VfkxF4nZw0FushaxCTo=}tion Online，2012（17）：1.

[6] PARKER T，HOOPES O，EGGETT D.The Effect of Seat Location and Movement or Permanence on Student-initiated Participation[J]. College teaching，2011，59（2）：79-84.

[7] KALINOWSKI S，TOPER M.L.The Effect of Seat Location on Exam Grades and Student Perceptions in an Introductory Biology Class[J]. Journal of College Science Teaching，2007，36（4）：54-57.

[8] LACROIX K.S，LACROIX. Does Seat Location Matter？ A Review of the Proximity Effect in Large and Small Classrooms[J]. Community College Enterprise，2017，23（2）：58-69.

[9] 刘慧凤，杨晓彤.座位选择与学习成绩相关研究——基于大学多课堂的自然试验研究证据[J].高教探索，2017（5）：43-48.

[10] 王映学，段宝军，张晓州.大学生课堂座位选择与学业成绩的关系研究[J].重庆高教研究， 2017，5（3）：65-72.

[11] ABEL BRODEUR，NIKOLAI COOK，ANTHONY HEYES.Methods Matter：P-Hacking and Publication Bias in Causal Analysis in Economics[J]. American Economic Review，2020，110（11）：3634-3660.

作者简介：李昌克（1989— ），男，浙江温州人，温州商学院助教，硕士，研究方向为银行经营管理；陈习定（1981— ），男，湖南娄底人，温州商学院教授，博士，研究方向为公司金融；陈凯鸣（1990— ），女，浙江温州人，温州商学院副教授，硕士，研究方向为公司金融。