新课标下基于HPM的大单元教学探究

摘 要：随着普通高中数学新课程标准的不断深入，大单元教学受到教育者越来越多的关注。文章探讨了在新课标背景下，结合HPM（History and Pedagogy of Mathematics）进行大单元教学的有效策略，并以“立体几何初步”为例进行了深入分析。通过引入数学史的相关内容，文章旨在丰富教学内容，在增强学生的学习兴趣的同时，促进学生对数学本质和数学文化的理解，使新课标的培养理念与核心素养目标融入高中数学课堂。

关键词：新课标；HPM；大单元教学；核心素养；立体几何初步

新课标表明，高中教育应着重提升学生的综合素质和学科核心素养。这就要求教育者跳出单一知识点的限制，把握整个单元的教学。大单元设计旨在整合知识体系，避免知识碎片化，确保教学设计与核心素养目标相契合。那么，在大单元教学设计中，如何能让这一单元的课时内容联系更加紧密、更具有整体性？教师需从某一核心点出发，用线串联各课时，构建完整的知识结构。同时，数学学科核心素养及综合素质的培养亦不可忽视。因此，在教学实践中，教师可以借助HPM这一途径，将数学学科核心素养的培养贯穿始终。

一、HPM在大单元教学中的价值

新课标指出，如何将数学史融入中小学的数学教学是数学教育领域的一个重要课题。数学史与数学教育之间的关系作为一个重要的研究领域，对发挥数学学科的育人功能、落实立德树人根本任务具有重要意义。近年来，HPM在数学教学中的重要价值在国内外均获得了广泛认可。2021年7月召开的第十四届国际数学教育大会（简称ICME-14）给教育者一个重要启示：数学史融入数学教学，对数学抽象、直观想象、逻辑推理、数学建模等核心素养的培养具有独特的作用，对教育教学和学生发展意义深远。

一是拓展学生的数学知识和视野。数学史和数学文化中有许多经典的数学问题和定理，通过介绍这些内容，可以让学生了解到更多的数学知识，并扩展他们的数学视野。二是培养学生的数学思维和解决问题的能力。数学史和数学文化中的数学问题和定理往往需要一定的思维和创新能力来解决，通过学习和讨论这些内容，可以培养学生的数学思维和解决问题的能力。三是培养学生的历史文化意识和素养。数学史和数学文化是数学发展的重要组成部分，通过介绍这些内容，可以培养学生对历史文化的理解和欣赏能力，提高他们的历史文化素养。四是增加学生对数学的兴趣和好奇心。通过讲述数学史和数学文化中的趣闻趣事，可以激发学生对数学的兴趣。五是培养学生的合作和交流能力。数学史和数学文化往往需要通过团队合作和交流才能全面理解，通过学习和探讨这些内容，可以培养学生的合作和交流能力。

然而，反观教学实际，高中数学教师对HPM的接受情况并不乐观，虽然他们已认识到其重要性，实际使用却少之又少。教材中很多关于数学史的案例并没有在授课中被充分利用，也就无法发挥其价值。另外，关于HPM的具体应用方法和策略，教师缺乏明确指导。因此，在新课标背景下，研究以HPM串联整个单元，是合理的且有必要的。教师可以通过认识、学习HPM的相关内容，培养学生的综合素质，提升数学核心素养。

二、基于HPM的高中数学“立体几何初步”大单元教学实践

立体几何是数学中的一个分支，主要研究物体的形状、大小、几何特性等。在传统教学方法中，教师一般通过讲述定义、公式和例题的方式进行授课。然而，由于立体几何对学习者的空间想象能力要求较高，且具有抽象性的特点，这种教学方法就会存在某些局限性，学生往往容易产生厌倦情绪，并且难以将所学知识与实际生活中的问题联系起来。

从HPM的视角研究“立体几何初步”的大单元教学可以发现，在人教A版（2019）必修第二册“立体几何初步”这一单元中，共有6节内容，具体细分为16个课时。教材中编写有3份HPM相关资料，分别是“画法几何与蒙日”“祖暅原理与柱体、椎体的体积”“欧几里得《原本》与公理化方法”。另有“文献阅读与写作”部分涉及HPM内容：几何学的发展。

教师在设计大单元教学时，可以充分利用这些材料，对本章内容进行整合构思：学习本单元前，教师先让学生通过查阅资料，自主学习几何学相关内容，了解几何学的发展史，知道发展历程中的关键点、具有划时代意义的结论及思想方法。这一过程可以让学生主动了解本单元的主要内容，了解学习背景，明确学习重点。这样，对立体几何的引入就不显得生硬。同时，通过前期的学习准备和书中第一节呈现的大量实物模型，很容易就能激发学生对这一单元的学习兴趣。

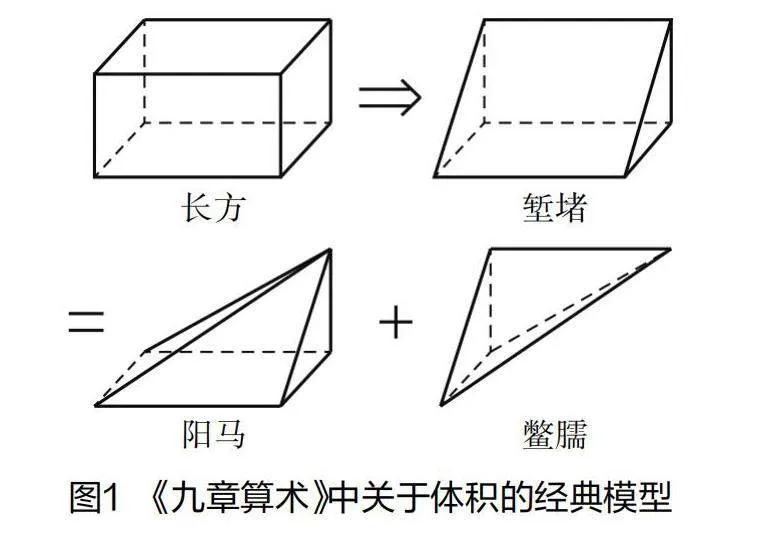
在兴趣的驱动下，教师进一步讲解蒙日与画法几何的关系，使学生在数学历史文化背景的熏陶下，产生强烈的求知欲，进而自然过渡到直观图的学习。进入“简单几何体的表面积与体积”章节时，为避免知识跨度过大，教师可借鉴《九章算术》中体积、容积的经典模型作为引入（见图1），这一方法不仅贴近学生已有的知识体系，还能有效衔接新旧知识，使学习过程更加顺畅。

图中“长方”“堑堵”“阳马”“鳖臑”之间蕴含的体积关系是我国古代人民的智慧结晶。而探求这一体积比的过程，正是学生学习第三节内容的过程。此时，教师用“祖暅原理”解释柱体、锥体之间的关系，学生很容易就能理解V柱=Sh与V锥=½Sh之间⅓的体积关系。在求解中可以得到V长方∶V堑堵∶V阳马∶V鳖臑=6∶3∶2∶1。教师启发学生观察这一组模型中柱体与椎体的体积比，还能发现其中蕴含的两个3∶1的关系，又进一步加深了本节课的基本知识。通过对HPM的学习，不仅帮助学生透彻理解了体积问题的内在联系，更在提升他们的直观想象和逻辑推理能力的同时，引发对中华文化的深切赞同。通过教师的正确引导，这一过程更升华至立德树人的高度，为学生的全面发展奠定坚实基础。

进入对“空间点、直线、平面之间位置关系”的探索后，教师可以讲述欧几里得的《原本》与公理化方法，使学生感受理性思维对数学发展的意义，再通过具体学习立体几何中的逻辑论证，体会公理化方法对数学研究的重要性，有助于进一步发展学生的数学核心素养。在本单元结束时，教师可以从HPM角度给学生设置一个开放性的探究话题：“几何学演变至今，有哪些分支？你感兴趣的是哪一方面？”教师可以结合教学实际，组织学生进行探究结果汇报展示，可以是小课题的形式，也可以是整理成文，以PPT的形式进行展示。相比于数学的专业知识，对HPM的研究较为简单，内容也更丰富，能让更多的学生参与进来，也能在交流展示中提升其综合素质。这也是HPM教学法为教师提供的一个培育学生核心素养的重要切入点。

至此，基于HPM的“立体几何初步”大单元设计就完成了，具体过程如表1所示。

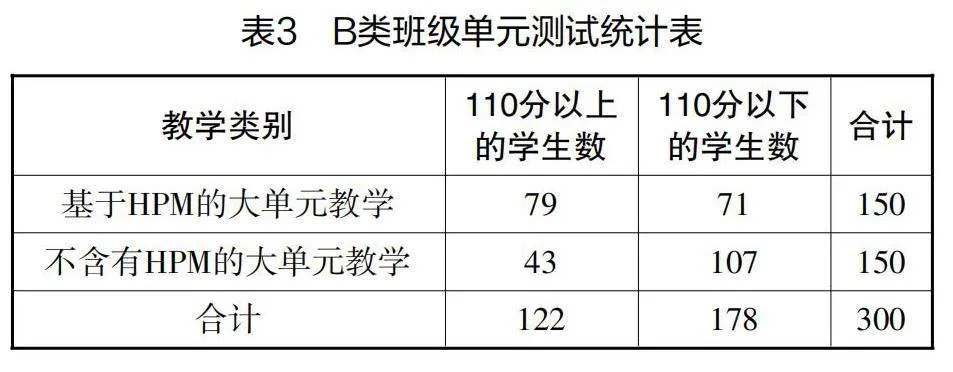
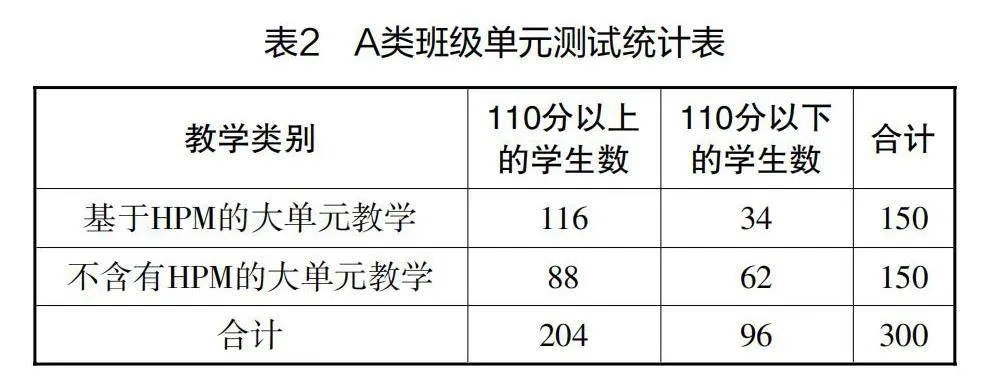
在教学实践中，本研究针对以上大单元设计，在A类班级（学习基础扎实、学习能力强）和B类班级（学习基础薄弱、学习能力弱）分别设置实验组和对照组，观察基于HPM的大单元教学对学生学习的助益性大小。在单元教学结束后，编写了一份“立体几何初步单元检测卷”，将数学核心素养相关考察点也融入试卷，满分150分。检测结果如下表所示：

由皮尔逊相关系数可知，教学类别与学生的检测成绩呈现出很明显的相关性。通过表2和表3可以发现，基于HPM的大单元教学无论是对A类班级学生还是对B类班级学生，影响都是显著的。同时，运用HPM进行大单元教学对B类班级学生的影响更大，这与B类班级学生的学习特点——接受新知的速度较慢、学习热情难以持久等是相符合的。教师用HPM将各个课时的内容联系在一起，可以使B类班级学生保持更持久的学习热情和更积极的学习态度。

此外，通过考查学生数学核心素养可以发现，参与实验的学生在数学抽象思维、直观想象能力以及逻辑推理等方面均实现了显著的提升。具体表现为在立体几何证明问题以及判断空间中点、线、面位置关系的典型题目中，平均分比没有参与实验的学生高5至10分。任课教师对参与实验的学生反馈信息也很好。

通过本次实践，教师的收获也很多。一方面，教师对教材的理解更为全面，备课时会从单元角度出发，对教材内容进行整体规划和统筹安排，并适时补充相关内容，使课堂教学更具吸引力。另一方面，教师对HPM的研究也更为深入，能够从中发现更多培养核心素养的契机，进一步提升教学质量。

三、基于HPM的大单元教学思考

第一，大单元教学可以通过HPM路径真正发挥统筹全局的作用。在教学实践中，教育者应当重视HPM的价值，在教材提供的HPM材料的基础上，可适当结合课外内容，使HPM像单元新知识一样，形成完整的知识链，连接起单元中的各个课时。

第二，HPM的教学方式，对激发学生学习数学的积极性、促进学生主动学习大有裨益。同时，它在提升学生综合素质、数学核心素养方面更是成效显著。在教学中，教师可以利用HPM教学激发学生兴趣，推动课堂从“教师主导”向“学生主体”转变，并充分发挥HPM教学在立德树人根本任务中的优势。

第三，基于HPM的大单元教学，也有助于提升教师的专业水平和综合素质。在对HPM的探究及应用中，已有一些研究者关注到HPM对促进教师MKT（Mathematical Knowledge for Teaching）发展的影响，教师在推广使用基于HPM的大单元教学时也应注意到这一点，确保师生双方均能从中受益。

第四，在设计大单元教学时，教师需要考虑HPM的使用场景。尽管书中HPM材料多出现在课时后，但教师应根据内容特性，灵活选择其作为引入案例、定义、背景或课后延伸材料，以充分发挥其作用。

第五，在大单元教学理念逐步推广的当下，教师应积极寻求其高效实施策略，确保教学流程清晰，整体性强，便于学生接受与实施。

在具体教学中，如何让数学学科核心素养落到实处，是教师和教育学者一直探索的重点。先让学生了解数学史，再做数学的研究，能够激发他们的学习兴趣和内在动力，促使他们更加主动地投入学习。在教学中，教师要深入挖掘教材中数学史料蕴含的教育意义，在教授文化知识的同时，培养学生的数学学科核心素养，真正实现教书育人。

参考文献：

［1］ 崔允漷. 如何开展指向学科核心素养的大单元设计［J］. 北京教育：普教版，2019（02）：11-15.

［2］ 中华人民共和国教育部. 普通高中数学课程标准：2017年版2020年修订［M］. 北京：人民教育出版社，2020.

［3］ 王艳芝，张春莉，高方方. 数学史视角下学科育人的实施路径［J］. 教育科学研究，2022（07）：59-65.

［4］ 冯晓华，袁敏. 关于HPM和PME结合的研究［J］. 西北大学学报：自然科学版，2005（05）：171-174.

［5］ 刘思璐，汪晓勤. 基于国际视角的数学史与数学教育研究现状分析：ICME-14之HPM专题综述［J］. 数学教育学报，2022，31（04）：98-102.

［6］ 邹大海，夏庆卓. 刘徽对《九章算术》中立体的辨名［J］. 自然辩证法通讯，2021，43（04）：47-54.

［7］ 蒲淑萍，汪晓勤. HPM视角教师专业发展的研究与启示［J］. 数学教育学报，2015，24（03）：76-80.

（责任编辑：廖 艺）