互补空间信息和隶属度修正的直觉模糊聚类苗族服饰图案分割

摘 要：苗族服饰图案分割对推动苗族服饰文化的数字化保护和传承具有重要意义。针对直觉模糊聚类算法鲁棒性差、对噪声敏感的问题，提出一种基于互补空间信息和隶属度修正的直觉模糊聚类苗族服饰图案分割算法。首先，该算法使用互补空间信息的加权平方欧式距离代替传统欧氏距离，用于提高算法的抗噪性能；其次，采用隶属度连接机制，减少算法的迭代次数，从而提升算法的运行速率；最后，利用图像的局部像素特征和空间关系，对邻域内的像素点赋予不同的权重来修正隶属度函数，以实现更为准确的分割。当混合噪声的密度为10%时，所提算法在合成图像数据集上的分割精度达到99.72%，在苗族服饰图案数据集上的划分系数和划分熵为97.23%和4.61%。结果表明，与相关算法相比，所提算法的分割精度更高、细节保留能力更强。

关键词：直觉模糊聚类；苗族服饰；分割；噪声；互补空间信息

中图分类号：TP391.4

文献标志码：A

文章编号：1009-265X（2024）10-0114-11

苗族服饰图案作为苗族文化的重要载体，具有极高的艺术价值和历史意义。随着时间的流逝，苗族服饰图案面临着自然老化、人为破坏和灾害等多重威胁，其完整性和真实性岌岌可危。数字化技术不仅可以提升苗族服饰图案的保存质量，还能扩大其传播范围，让更多人认识并传承苗族服饰文化。通过精准分割苗族服饰图案，可以深入理解图案的文化内涵和美学价值，为现代设计提供丰富的灵感来源，同时促进苗族服饰文化的传承与创新，推动文化多样性和艺术交流的发展，进而丰富学术研究内容，并为相关领域的技术进步提供有力支持。然而，苗族服饰作为一种特殊的服装类型，有其丰富独特的纹样、色彩及图腾等重要元素特征，无疑增加了分割的难度，再加上图像采集的不完善、光照以及成像设备等因素的影响，给图像分割带来一定的挑战。

图像分割是图像分析的关键步骤，广泛应用于民族服饰［1］、医疗诊断［2］和交通运输［3］等领域。近年来，模糊C均值（Fuzzy C-Means，FCM）聚类算法［4-5］因其简单性和高效性，在图像分割领域得到了广泛应用。但FCM算法容易陷入局部最优解且对噪声敏感，因此涌现出许多FCM的改进算法。例如，Lei等［6］提出一种快速鲁棒的FCM（Fast and Robust FCM，FRFCM）聚类算法。对于大部分图像，该算法的分割效果较好，完成时间短。Feng等［7］提出一种偏差校正嵌入FCM（Bias Correction Embedded FCM with Spatial Constraint，BCEFCM_S）聚类算法，该算法根据邻域对偏差隶属度引入空间约束，以消除噪声对分割性能的影响。随着模糊聚类算法的不断发展，隶属度单一性的局限性也逐渐显现。

Atanassov［8］提出直觉模糊集（Intuitionistic Fuzzy Set，IFS）的概念。IFS将隶属度、非隶属度和犹豫度同时考虑在内，弥补了模糊集只考虑隶属度的不足。Chaira［9］通过引入不确定性和直觉模糊熵两种思想，提出直觉模糊（Intuitionistic FCM，IFCM）聚类算法，该算法能精确地描述数据的不确定性和模糊性，但与FCM算法类似，抗噪性能较差。为此，Wu等［10］提出基于IFS的可信直觉模糊（Credibilistic Intuitionistic FCM，CIFCM）聚类算法。Lei等［11］通过核函数的思想，提出核距离的直觉模糊（Kernel Intuitionistic FCM，KIFCM）聚类算法。CIFCM和KIFCM算法虽然一定程度上提高了聚类性能，但由于未考虑空间信息，在处理噪声图像时的分割质量仍存在不足。随后，Arora等［12］将空间信息纳入直觉模糊集，提出增强空间直觉模糊（Spatial Intuitionistic FCM，SIFCM）聚类算法，该算法使用新的模糊补计算非隶属度，进一步增强了算法的抗噪性能。在此基础上，彭家磊等［13］引入隶属度约束惩罚项，采用核距离作为度量方式，提出一种隶属度修正的空间核直觉模糊（Spatial Kernel Intuitionistic FCM，SKIFCM）聚类算法并应用于苗族服饰图案的分割，该算法的抗噪性能较好，但分割彩色苗族服饰图案的时间较长，分割精度也有待提高。覃小素等［14］提出基于空间信息的鲁棒FCM（Robust FCM based on Spatial Information，RFCM-S1）聚类算法分割苗族服饰图案，该算法融入空间信息，对简单的和低强度噪声污染的苗族服饰图案具有较好的分割结果，但对复杂的和高强度噪声污染的苗族服饰图案的分割结果还不够理想。

为了快速、精确的分割苗族服饰图案，本文提出一种基于互补空间信息和隶属度修正的直觉模糊（Intuitionistic FCM based on Complementary Spatial Information and Membership Modification，IFCM_CSM）聚类苗族服饰图案分割算法。该算法采用鲁棒性更强的互补空间信息的加权平方欧氏距离作为度量方式，并引入隶属度连接机制以降低算法的迭代次数。通过与4种FCM相关算法进行对比，验证所提算法在分割性能、分割精度以及保持图像细节能力方面的显著优势。

1 模糊聚类的相关技术

1.1 FCM算法

FCM算法允许同一数据属于多个不同的类，是一种无监督的模糊聚类方法，在算法实现过程中不需要人为干预。它的目标函数如下：

minJU，V=∑ck=1∑ni=1μmki‖xi-vk‖2，∑ck=1μki=1（1）

式中：U表示模糊隶属度矩阵，V表示聚类中心矩阵，c表示聚类数目，n表示总像素数目，m是模糊隶属度指数，μki表示第i个像素xi到第k个聚类中心的隶属度，‖xi-vk‖2表示像素xi到聚类中心vk的欧氏距离。

使用拉格朗日最小乘子法对式（1）进行求解，得到模糊隶属度和聚类中心的更新表达式如下：

μki=∑cl=1（‖xi-vk‖2/‖xi-vl‖2）-1/（m-1）（2）

vk=∑ni=1μmkixi/∑ni=1μmki（3）

1.2 直觉模糊理论

直觉模糊理论引入了隶属度函数和非隶属度函数，用以描述一个元素属于某个集合的程度，以及不属于该集合的程度。这一理论比传统的模糊集合更具有灵活性和实用性，因为它同时考虑了隶属度和非隶属度，能够更精确地处理各种不确定性问题。设X=｛x x …，xn｝表示一个有限论域，则Z在集合X中的IFS被定义为：

Z=｛（x，μZ（x），vZ（x））|x∈X｝（4）

式中：μZ（x）→［0，1］，vZ（x）→［0，1］分别表示元素x对于集合Z的隶属度函数和非隶属度函数。为了确保直觉模糊集的完整性，每一个元素x∈Z都必须满足0≤μZ（x）+vZ（x）≤1。对于集合Z中的每一个x，若存在μZ（x）=1-vZ（x），那么直觉模糊集便退化为传统的模糊集。为了更准确地描述数据之间的不确定性，Atanassov引入了犹豫度，其表达式如下：

FZ（x）=1-μZ（x）-vZ（x），0≤FZ（x）≤1（5）

在已有的直觉模糊理论中，Maheshan等［15］通过Yager生成函数，提出新的非隶属度计算表达式：

vZ（x）=［1-μZ（x）β］1/β，β∈（0，+∞）（6）

因此，将式（6）代入式（5），犹豫度变为：

FZ（x）=1-μZ（x）-［1-μZ（x）β］1/β（7）

式中：β表示非隶属度控制指数。

1.3 IFCM聚类算法

直觉模糊熵是衡量模糊集中模糊性的度量，许多研究者从不同角度进行了定义。其中，Pal等［16］深入研究了经典的香农信息论，并引出了指数熵的概念。对于一个概率分布：p=pi（i= …，n），指数形式的香农熵可定义如下：

L=∑ni=1pie（1-pi）（8）

将指数形式的香农熵与IFS理论相结合，得到直觉模糊熵的表达式如下：

L（Z）=∑ni=1FZ（xi）e［1-FZ（xi）］（9）

IFCM算法在传统FCM算法的基础上，通过引入犹豫度函数，进一步扩展了聚类的灵活性。其目标函数的表达式为：

minJU，V=∑ck=1∑ni=1μ*mki‖xi-vk‖2+∑ck=1F*ke1-F*k（10）

式中：F*k=∑ni=1Fki/n，Fki为第k个类中第i个像素的犹豫度。通过优化目标函数式（10），可以得到隶属度函数和聚类中心的更新表达式如下：

μ*ki=μki+Fki（11）

ol6+ZfkvT6aCw/ShP5K/5iPS2I7bHxIK8+pripinpmM=

v*k=∑ni=1μ*mkixi/∑ni=1μ*mki（12）

1.4 隶属度连接

在FCM算法中，为了最小化目标函数，使用了拉格朗日乘子法，并推导出了更新隶属度和聚类中心的表达式，最终使目标函数能够最小化。然而，在很多情况下，迭代次数并没有被充分考虑。为此，文献［17］提出一种隶属度连接机制，即利用前一次迭代计算出的隶属度之和来减少迭代次数。隶属度连接的表达式可表示为：

M=∑Ne=1uke（13）

对于一个给定的图像，图像的尺寸越大，所有像素的隶属度之和就越大，这就意味着目标函数值会较小，会造成目标函数提前收敛的情况。为了解决这个问题，可以将式（13）修改为对数形式。具体来说，可以将目标函数中的隶属度之和取对数，从而避免目标函数提前收敛的情况。式（13）修改后的表达式为：

M=ln∑Ne=1uke+1（14）

为了进一步增大式（14）的变化，可以对其进行平方：

M=ln2∑Ne=1uke+1（15）

1.5 互补空间信息的加权平方欧氏距离

在FCM算法中，传统欧式距离对噪声较为敏感，所以在噪声环境中，FCM算法的抗噪性能差，分割结果差。近年来，Wu等［18］充分考虑空间信息的互补性，这种互补性体现在他们巧妙地将邻域均值和中值融合起来，以构建一种具有互补空间信息的加权平方欧氏距离。该距离不仅融合了空间信息，对噪声还具有较强的抑制能力，表达式如下：

d2ki=η1‖xi-vk‖2+η2‖x-i-vk‖2+η3‖x^i-vk‖2（16）

式中：ηl表示距离权重系数，满足0≤ηl（l= 3）≤1且∑3l=1ηl= x-i和x^i分别是当前像素xi的邻域均值和中值。

2 IFCM_CSM算法

2.1 IFCM_CSM算法的目标函数构造

许多IFCM的改进算法引入了核函数，这有利于将低维空间中的非线性问题转变为高维空间中的线性问题，从而提高该算法的聚类性能。然而，核函数的引入增加了计算复杂度，导致运行效率降低。同时，核函数的引入只能一定程度上减轻对噪声的敏感性，面对密度较大噪声，通常得不到较好的分割结果。为此，本文对IFCM算法的目标函数进行了改进，将传统欧氏距离替换为更具鲁棒性的互补空间信息的加权平方欧式距离。此外，为了提高算法的效率，引入隶属度连接机制，以达到减少迭代次数的目的。最后，给像素点赋予了不同的权值，进一步优化了隶属度函数的计算。基于这些改进，提出一种基于互补空间信息和隶属度修正的直觉模糊聚类苗族服饰图案分割算法（IFCM_CSM），算法的目标函数如下：

minJU，V=∑ck=1∑ni=1μ*mkiη1‖xi-vk‖2+η2‖x-i-vk‖2+η3‖x^i-vk‖2+∑ck=1F*ke1-F*kln2∑Ne=1uke+ ∑ck=1μ*ki=1（17）

式中：ηl（l= 3）是距离权重系数，F*k=1n∑ni=1Fki，Fki为第k个类中第i个像素的犹豫度，其余参数含义与FCM算法一样。

为了最小化目标函数式（17），采用拉格朗日乘子法得到更新隶属度和聚类中心的表达式如下：

μ*ki=1-1-ln2∑Ne=1uke+1/η1‖xi-v*k‖2+η2‖x-i-v*k‖2+η3‖x^i-v*k‖21m-1∑ckln2∑Ne=1uke+1/η1‖xi-v*k‖2+η2‖x-i-v*k‖2+η3‖x^i-v*k‖21m-1β1β（18）

v*k=∑niμ*kiη1xi+η2x-i+η3x^i/∑niμ*ki（η1+η2+η3）（19）

由于图像中的像素是相互关联的，并且属于同一类别的像素往往聚集在一起，因此考虑像素周围的隶属度有助于增强算法的聚类性能。在本文中，根据图像中局部像素的特征来调整式（18）中得出的隶属度函数。通过这种方式，可以更准确地识别和分类像素，从而提高聚类的效果。空间函数的表达式如下：

hki=∑l∈NB（xi）μkl（20）

式中：NB（xi）表示空间域中以xi为中心的正方形窗口，hki与隶属度是一样的，表示像素xi到第k个类的概率。

在不改变目标函数式（17）的情况下，将式（20）与式（18）相结合，得到更新隶属度函数和聚类中心如下：

μ*ki′=μ*pkihqki/∑clμ*plihqli（21）

v*k′=∑ni=1μ*ki′xi/∑ni=1μ*ki′（22）

式中：参数p和q用于调节两个函数的贡献程度。在同质区域内，空间函数对图像的作用相对较小，主要是简单地强化初始隶属度函数。然而，对于噪声点，利用像素的邻域信息来降低它们的权值，从而有效地消除噪声对图像的影响。

2.2 IFCM_CSM算法的执行步骤

a）设置聚类数目c，模糊隶属度指数m，最大迭代次数T和终止条件ε，邻域大小w。

b）随机初始化模糊隶属度矩阵U。

c）设置循环计数器，初始化r=0。

d）利用式（7）计算犹豫度。

e）根据式（15）计算隶属度连接。

f）根据式（22）更新模糊聚类中心。

g）根据式（21）更新模糊隶属度。

h）根据式（17）更新目标函数。

i）当||Jr+1-Jr||<ε，或者r>T时，终止迭代过程，否则转向步骤d），直至迭代结束。

3 实验结果与分析

3.1 实验设计与数据来源

为了验证本文算法良好的图像分割性能，设计了3组实验进行验证：含噪的合成图像分割、含噪的苗族服饰图案分割和彩色苗族服饰图案分割。其中，合成图像的数据集来源于文献［19］，苗族服饰图像的数据集来源于北京服装学院民族服饰博物馆（http：//www.biftmuseum.com/）。

3.2 实验环境与参数选取

选择合适的参数对于实验结果具有至关重要的影响。在本文中，对比算法的参数选取均参考原文，并适当改变，经多次运行确定最优的参数。对于IFCM_CSM算法的参数选取，采用了固定参数和可变参数的组合，以便更好地适应实验需求。

a）固定参数：由于IFCM_CSM算法的部分参数对实验结果的影响较小，因此凭经验设置。例如，模糊隶属度指数m=2，终止条件ε=1e-5，最大迭代次数T=200，聚类数目c=2，邻域窗口大小w=5。反之，对实验结果影响较大的参数，可通过参考文献选取。例如，非隶属度控制指数β=0.8［20］，距离权重η1=0.5，η2=η3=0.25［18］。这些参数在实验中保持不变，以确保实验结果的稳定性和可重复性。

b）可变参数：贡献程度指数p和q的值需要根据实验情况选取，其选取范围可参考文献［21］。通过调整p和q的值，可以更好地控制算法的性能和分割效果，以满足不同实验场景的需求。

c）实验环境配置：使用MatLab R2018a软件，运行在Windows 10操作系统上，处理器为Intel（R） Core（TM） i5-7200U CPU @ 2.50GHz 2.7 电脑的运行内存为8 GB。

3.3 评价指标

为了全面评估所提算法在图像分割方面的性能，采用了3个在图像分割领域中广泛使用的指标，对分割结果进行定量分析。指标分别是划分系数（Partition Coefficient，VPC）、划分熵（Partition Entropy，VPE）［22］和分割精度（Segmentation Accuracy，SA）［23］。

3.4 合成图像分割

为了验证IFCM_CSM算法的抗噪性能，本文在合成图像中分别添加5%、8%和10%的混合噪声（高斯噪声、椒盐噪声）进行实验，并将分割结果与相关算法进行对比。合成图像的实验参数p和q均分别设置为3和1。

图1展示了不同算法在不同混合噪声密度下的分割结果，从图中可以看出，FCM和IFCM算法的分割结果存在大量的噪声点，这是因为它们未考虑空间信息，对噪声较为敏感。KIFCM算法采用核距离度量来替代欧氏距离，在一定程度上提高了分割效果。而SKIFCM算法则进一步考虑了空间信息，并使用了更为鲁棒的核距离度量，因此分割结果也有所改善。相比之下，IFCM_CSM算法的分割结果非常清晰，基本上不存在噪声点。这是因为该算法采用了互补空间信息的加权平方欧式距离来替代传统欧式距离，并充分考虑了空间信息，对像素点的隶属度进行修正。这种改进使得该算法具有更好的抗噪性能，从而得到了更加优秀的分割结果。

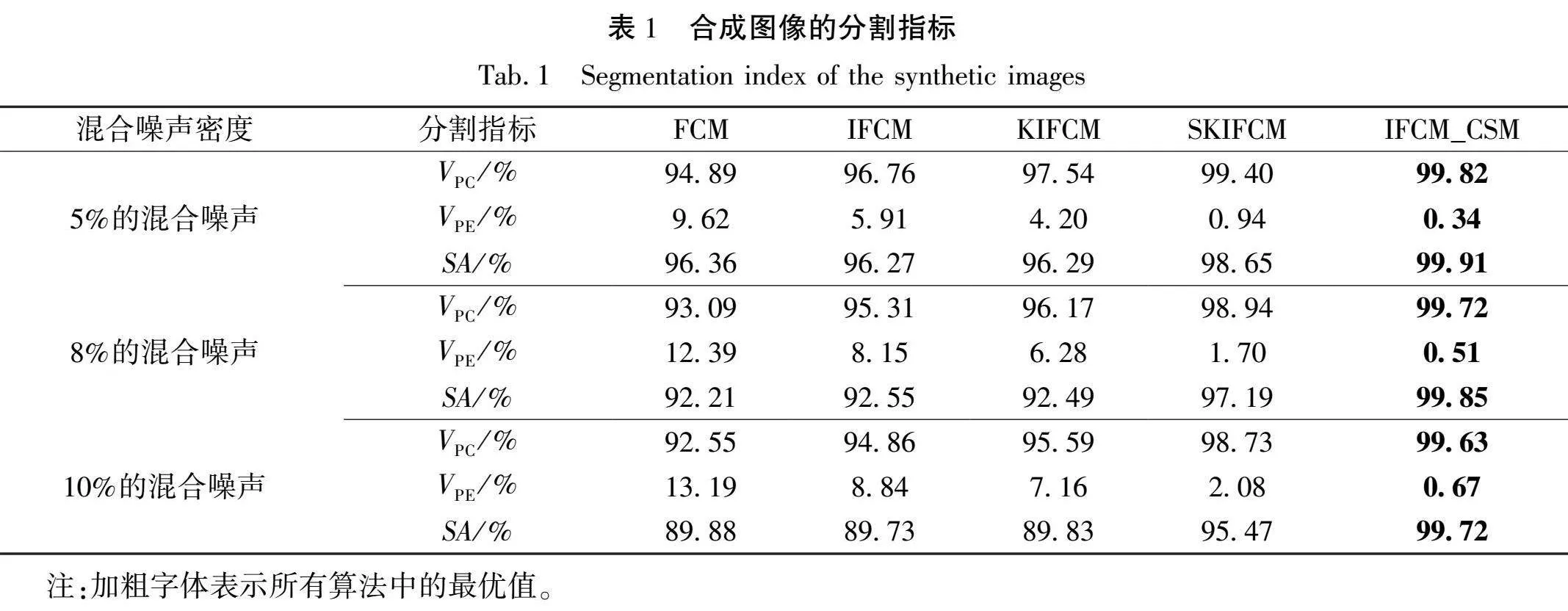
表1为不同算法在分割合成图像时的分割性能指标，从表中可以看出，随着混合噪声密度的增加，各个算法的分割性能指标都呈现出一定的下降趋势。然而，相较于其他算法，IFCM_CSM算法在混合噪声密度增加的情况下仍然能够保持相对稳定的性能表现。具体来说，IFCM_CSM算法的VPE达到了约99.72%，VPC为0.51%，SA更是高达99.83%。与SKIFCM算法相比，IFCM_CSM算法的VPC、VPE和SA这3个分割性能指标均有提高，且SA提高了约2.73%。这一显著提升再次证明了IFCM_CSM算法具有卓越的抗噪性能和分割精度。

3.5 不同类型噪声的苗族服饰图案分割

苗族服饰图像可能受到各种噪声的干扰，如摄像设备的限制、环境光照条件的变化等，这些噪声可能对图像的视觉效果和后续处理产生负面影响。为了评估IFCM_CSM算法在处理受噪声干扰的苗族服饰图像方面的性能，本文通过对简单的苗族服饰

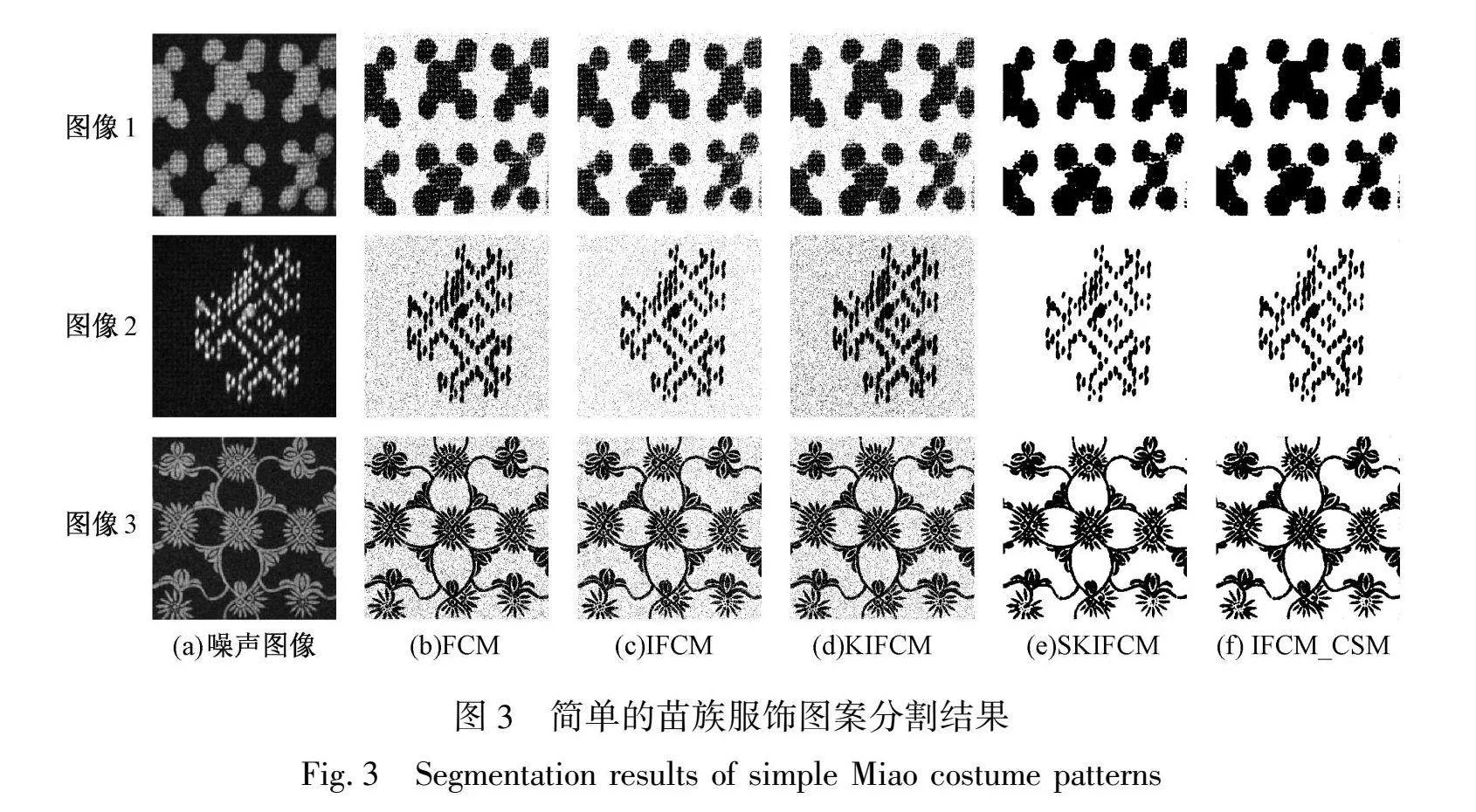
图案和复杂的苗族服饰图案添加不同类型的噪声进行实验，添加的噪声类型分别是密度为10%的高斯噪声、10%的椒盐噪声和10%的混合噪声（高斯噪声和椒盐噪声）。其测试的噪声图像如图2所示，分割结果如图3和图4所示。本节的实验参数p和q均分别设置为3和1。

从图3和图4中可以看出，FCM、IFCM、KIFCM算法的分割结果中存在大量噪声点，分割质量相对较差。这是因为这些算法并未考虑到空间信息，导致对噪声的鲁棒性较差。相比之下，SKIFCM和IFCM_CSM算法在分割结果中几乎不包含噪声点，且分割结果更为清晰。这归功于SKIFCM和IFCM_CSM算法在考虑空间信息的基础上，对隶属度进行了修正，从而提高了分割的准确性。

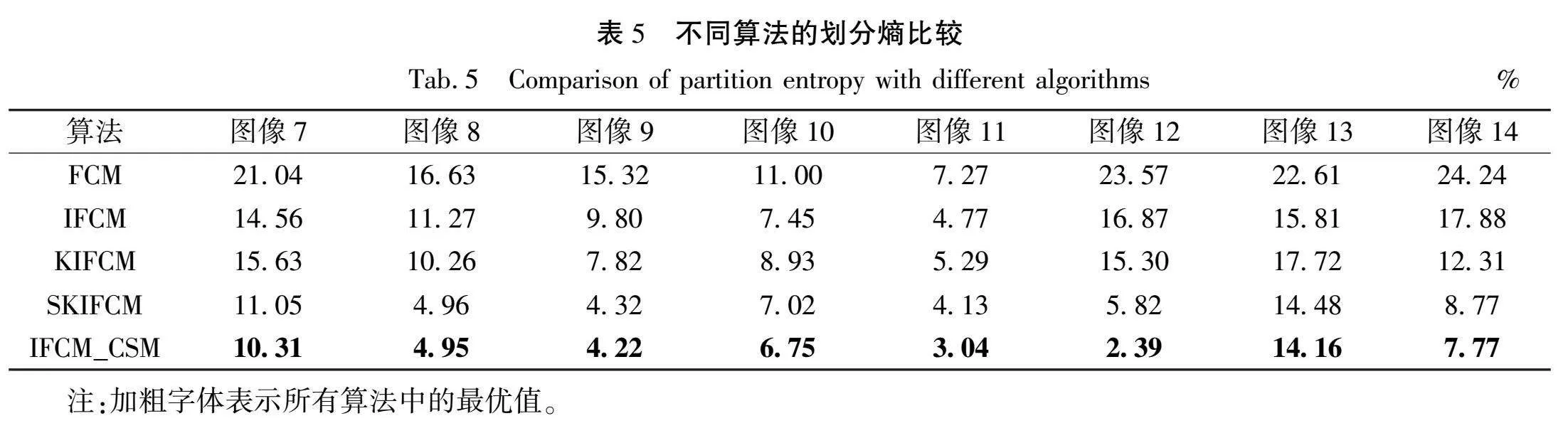
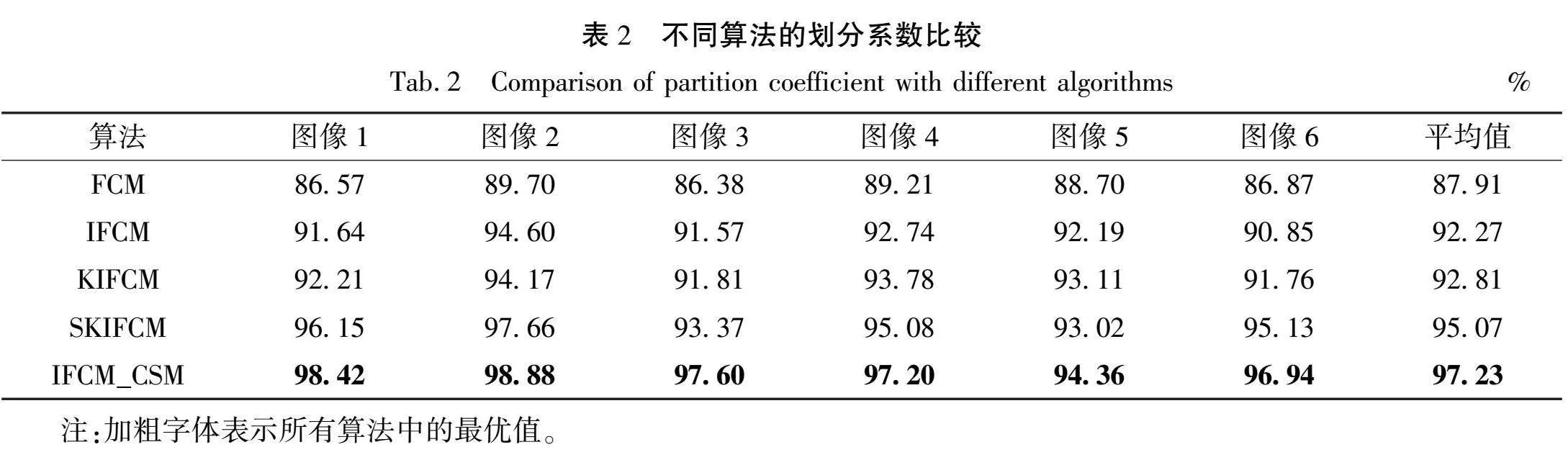
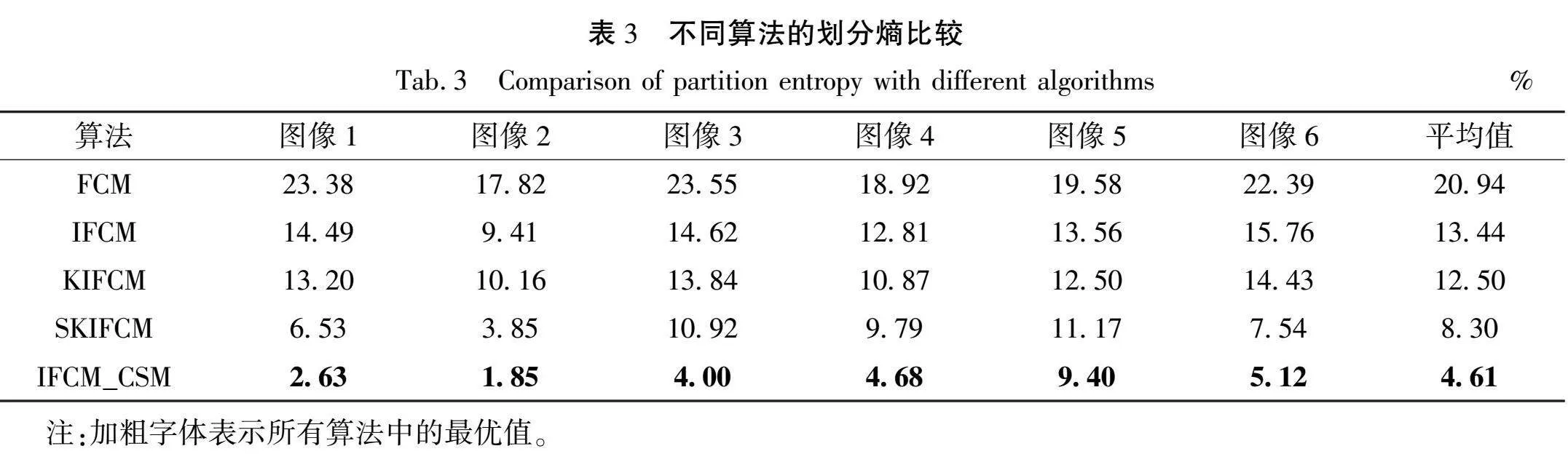
从表2和表3中可以看出，在不同噪声环境下，IFCM_CSM算法在VPC和VPE方面的表现均优于其他相关算法。具体而言，IFCM_CSM算法的VPC和VPE的平均值分别为97.23%和4.61%，这与其他相关算法有着明显的区别。同时，通过视觉效果和性能指标的评估可以看出，IFCM_CSM算法具有较好的抗噪性能，对于带有噪声的苗族服饰图案，该算法能够实现良好的分割效果，这表明IFCM_CSM算法在处理带噪声的苗族服饰图案方面具有较高的准确性和稳定性。

3.6 彩色苗族服饰图案分割

为了比较不同算法在苗族服饰图案分割方面的性能表现，本文选取8幅不同类型的苗族服饰图案进行实验。同时，将IFCM_CSM算法与4种相关算法的分割结果进行了比较分析。图像9和图像12的实验参数p和q分别为3和 图像11的实验参数p和q分别为2和 其余图像的实验参数p和q均分别为1和1。

从图5中可以观察到，FCM、IFCM和KIFCM算法的分割结果中都包含了不少伪斑点，这些伪斑点使得分割结果不够清晰和准确。相比之下，SKIFCM和IFCM_CSM算法的分割结果则更为清晰，基本上不存在伪斑点，并且在去除伪斑点的同时，还保留了丰富的图案细节。这是因为SKIFCM算法和IFCM_CSM算法都考虑了空间邻域信息，并对像素点的隶属度进行了修正。实验结果表明这2种算法在分割过程中能够更好地抑制伪斑点，从而得到更为准确和可靠的分割结果。

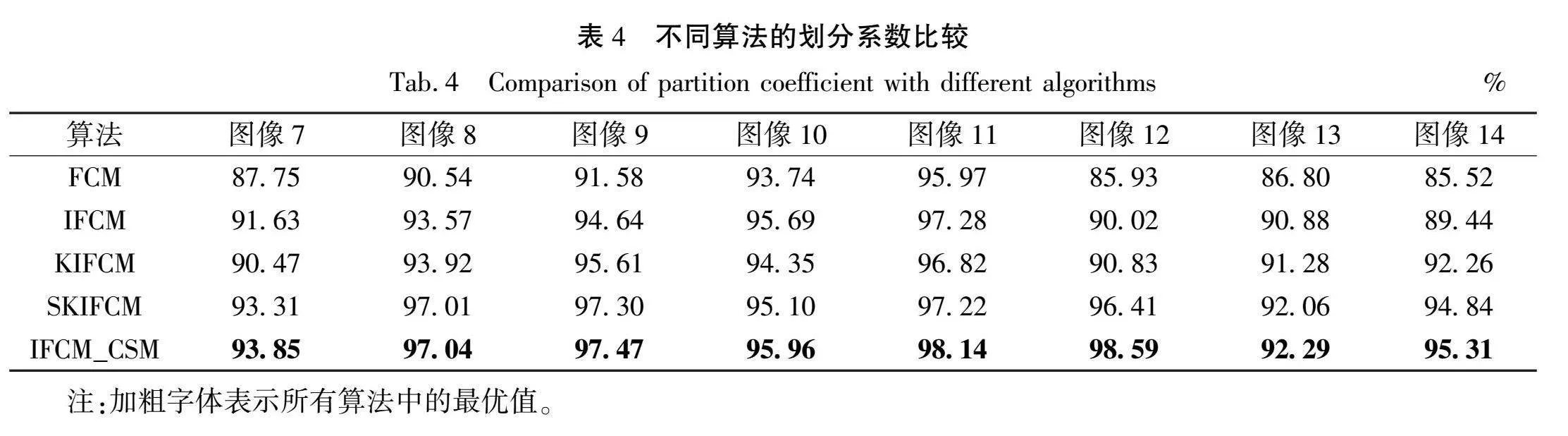
从表4和表5的数据对比中可以看出，FCM、IFCM和KIFCM这几种算法在性能指标上表现相对较低，SKIFCM算法的表现则相对较好。然而，与这些算法相比，IFCM_CSM算法在性能指标上达到了最优状态。具体来说，VPC和VPE分别为96.08%和6.70%。这一数据表明，与相关算法相比，IFCM_CSM算法的分割性能得到了显著的提升。这为苗族服饰图案分割领域带来了新的突破，为未来的研究提供了有益的参考。

3.7 运行效率分析

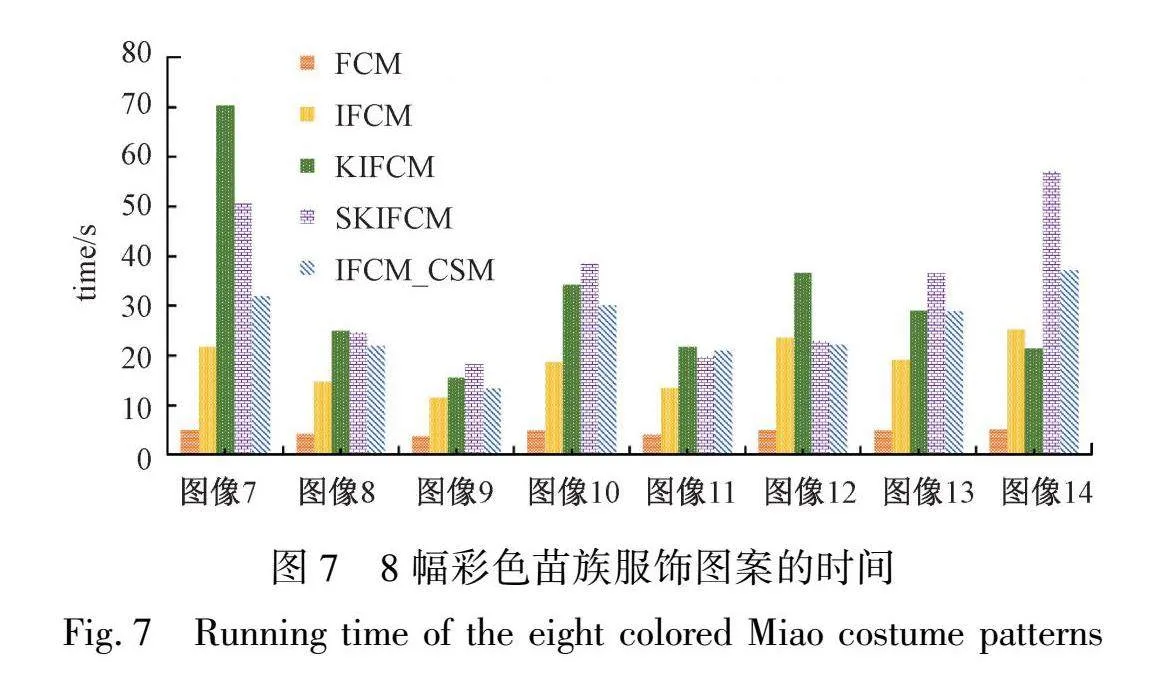
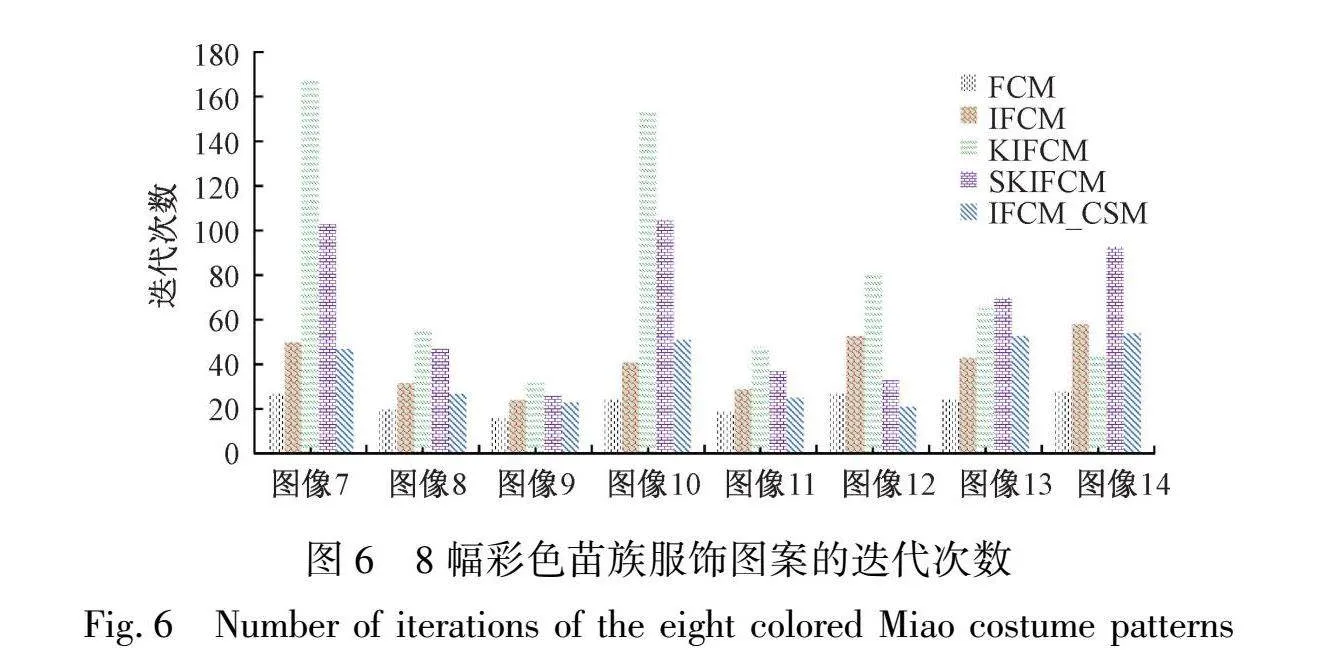
为了比较各算法的运行效率，详细记录了不同算法在图5中8幅图像的迭代次数和运行时间。从图6和图7的展示中可以看出，虽然FCM算法的迭代次数和运行时间相对较少，但其分割效果并不理想。相比之下，IFCM_CSM算法的迭代次数和运行时间明显优于KIFCM和SKIFCM算法。这是因为IFCM_CSM算法在计算过程中采用了隶属度连接机制，有效地降低了计算的复杂度，从而提高了算法的运行效率。这种机制不仅简化了计算过程，还保证了分割结果的准确性。

4 结论

本文提出一种基于互补空间信息和隶属度修正的直觉模糊聚类苗族服饰图案分割算法。该算法使用互补空间信息的加权平方欧氏距离作为度量方式，并采用隶属度连接机制，达到减少迭代次数的目的。在每次迭代过程中，利用图像的局部像素特征和空间关系，对每个像素点的隶属度进行修正，以实现更为准确的分割。实验结果表明，与相关算法相比，本文所提算法在合成图像和苗族服饰图案上均展示了良好的分割性能，不仅能消除噪声的影响，而且还能保留丰富的图像细节。色彩鲜艳、复杂的苗族服饰图案在苗族服饰中具有很高的适用性，不仅是苗族文化传承的重要媒介，满足了社会交往和审美需求，更深刻体现了苗族人民的身份认同和文化自豪。

总的来说，本文所提算法为处理苗族服饰图案提供了一种先进、高效的技术手段，为苗族服饰文化的数字化保护和传承开辟了新的可能。未来，我们将持续优化算法性能，并探索其在更多领域的应用潜力。

参考文献：

［1］冯润， 黄成泉， 胡雪，等. 基于模糊拟合图像驱动的苗族服饰图像分割算法［J］. 现代纺织技术， 202 30（5）： 31-41.

FENG Run， HUANG Chengquan， HU Xue， et al. Image segmentation algorithm of Miao costumes based on fuzzy fitting image［J］. Advanced Textile Technology， 202 30（5）： 31-41.

［2］HE W， WANG X， WANG L， et al. Incremental learning for exudate and hemorrhage segmentation on fundus images［J］. Information Fusion， 202 73： 157-164.

［3］WANG Y， WANG Z， NAKANO Y， et al. Context enhanced traffic segmentation： Traffic jam and road surface segmentation from aerial image［C］//2022 IEEE 14th Image， Video， and Multidimensional Signal Processing Workshop （IVMSP）. Nafplio， Greece. IEEE， 2022： 1-5.

［4］彭家磊， 黄成泉， 雷欢， 等. 自适应空间强度约束和KL信息的模糊C均值彩色噪声图像分割［J/OL］. 控制与决策， DOI：10.13195/j.kzyjc.2023.1032.

PENG Jialei， HUANG Chengquan， LEI Huan， et al. Fuzzy C-Means with adaptive spatial intensity constraints and KL information for color noise image segmentation［J/OL］. Control and Decision， DOI：10.13195/j.kzyjc.2023.1032.

［5］GUO L， SHI P， CHEN L， et al. Pixel and region level information fusion in membership regularized fuzzy clustering for image segmentation［J］. Information Fusion， 2023， 92： 479-497.

［6］LEI T， JIA X， ZHANG Y， et al. Significantly fast and robust fuzzy C-means clustering algorithm based on morphological reconstruction and membership filtering［J］. IEEE Transactions on Fuzzy Systems， 2018， 26（5）： 3027-3041.

［7］FENG C， LI W， HU J， et al. BCEFCM_S： Bias correction embedded fuzzy c-means with spatial constraint to segment multiple spectral images with intensity inhomogeneities and noises［J］. Signal Processing， 2020， 168： 107347.

［8］ATANASSOV K T. Intuitionistic fuzzy sets［J］. Fuzzy Sets and Systems， 1986， 20（1）： 87-96.

［9］CHAIRA T. A novel intuitionistic fuzzy C means clustering algorithm and its application to medical images［J］. Applied soft computing， 201 11（2）： 1711-1717.

［10］WU C M， YANG X. Robust credibilistic intuitionistic fuzzy clustering for image segmentation［J］. Soft Computing， 2020， 24（14）： 10903-10932.

［11］LEI X X， OUYANG H L， Xu L J. Kernel-distance-based intuitionistic fuzzy c-means clustering algorithm and its application［J］. Pattern Recognition and Image Analysis， 2019， 29（4）： 592-597.

［12］ARORA J， TUSHIR M. An enhanced spatial intuitionistic fuzzy C-means clustering for image segmentation［J］. Procedia Computer Science， 2020， 167： 646-655.

［13］彭家磊， 黄成泉， 覃小素， 等. 隶属度修正的空间核直觉模糊聚类苗族服饰图案分割［J］. 毛纺科技， 2023， 51（9）： 117-125.

PENG Jialei， HUANG Chengquan， QIN Xiaosu， et al. Spatial kernel intuitionistic fuzzy clustering algorithm for Miao costume pattern segmentation with modified membership［J］. Wool Textile Journal， 2023， 51（9）： 117-125.

［14］覃小素， 黄成泉， 彭家磊， 等. 基于空间信息的鲁棒模糊C均值聚类的苗族服饰图像分割算法［J］. 毛纺科技， 2024， 52（1）： 91-98.

QIN Xiaosu， HUANG Chengquan， PENG Jialei， et al. Robust fuzzy C-mean clustering algorithm based on spatial information for segmentation of Miao costume image［J］. Wool Textile Journal， 2024， 52（1）： 91-98.

［15］MAHESHAN M S， HARISH B S. A modified intuitionistic fuzzy clustering approach for sclera segmentation［J］. SN Computer Science， 202 2（4）： 1-8.

［16］PAL N R， PAL S K. Entropy： A new definition and its applications［J］. IEEE Transactions on Systems， Man， and Cybernetics， 199 21（5）： 1260-1270.

［17］Wang Q S， Wang X P， Fang C， et al. Robust fuzzy c-means clustering algorithm with adaptive spatial & intensity constraint and membership linking for noise image segmentation［J］. Applied Soft Computing， 2020， 92： 106318.

［18］WU C M， ZHANG J. Robust semi-supervised spatial picture fuzzy clustering with local membership and KL-divergence for image segmentation［J］. International Journal of Machine Learning and Cybernetics， 202 13（4）： 963-987.

［19］WEI T Y， WANG X P， LI X N， et al. Fuzzy subspace clustering noisy image segmentation algorithm with adaptive local variance & non-local information and mean membership linking［J］. Engineering Applications of Artificial Intelligence， 202 110： 104672.

［20］张洁玉， 李佐勇. 基于核空间的加权邻域约束直觉模糊聚类算法［J］. 电子与信息学报， 2017， 39（9）： 2162-2168.

ZHANG Jieyu， LI Zuoyong. Kernel-based algorithm with weighted spatial information intuitionistic fuzzy C-means［J］.Journal of Electronics & Information Technology， 2017， 39（9）： 2162-2168.

［21］JI X， HUANG L， TANG B H， et al. A superpixel spatial intuitionistic fuzzy C-means clustering algorithm for unsupervised classification of high spatial resolution remote sensing images［J］. Remote Sens， 202 14（14）： 3490.

［22］WU C M， HUANG C C， ZHANG J J. Local information-driven intuitionistic fuzzy c-means algorithm integrating total bregman divergence and kernel metric for noisy image segmentation［J］. Circuits， Systems， and Signal Processing， 2023， 42（3）： 1522-1572.

［23］ZHU J X， WANG F， YOU H. SAR image segmentation by efficient fuzzy C-means framework with adaptive generalized likelihood ratio nonlocal spatial information embedded［J］. Remote Sensing， 202 14（7）： 1621.

Intuitionistic fuzzy clustering based on complementary spatial information and

membership modification for Miao costume pattern segmentation

PENG Jialeia，b， HUANG Chengquana，c， CHEN Yangb， QIN Xiaosub，

LEI Huanb， ZHENG Lanc， ZHOU Lihuab

（a.Key Laboratory of Pattern Recognition and Intelligent Systems of Guizhou Province;

b.School of Data Science and Information Engineering;

c.Engineering Training Center， Guizhou Minzu University， Guiyang 550025， China）

Abstract：

The segmentation of Miao costume patterns not only contributes to the protection and transmission of the unique Miao culture， but offers a wealth of materials and inspiration for artistic creation， brand promotion， and academic research. At the same time， through the segmentation of Miao costume patterns， the Miao history， culture and tradition can be better understood and spread， and the sense of national identity and cultural self-confidence can be enhanced. In addition， it contributes to digital preservation， providing new ideas and methods in the field of modern technology and the segmentation of national costumes. To address the poor robustness and noise sensitivity of the intuitive fuzzy clustering algorithm， a novel algorithm for the segmentation of Miao costume patterns was proposed， and it incorporated complementary spatial information and membership modification. Firstly， to enhance noise resistance， the algorithm innovatively employed a weighted squared Euclidean distance based on complementary spatial information instead of the traditional Euclidean distance calculation. In this way， the algorithm is able to more accurately measure the similarity between pixels， and effectively resist the interference of noise， thus achieving more accurate segmentation in complex and noisy images data. Secondly， to further improve the algorithm's efficiency， a membership connection mechanism was introduced. The core idea of this mechanism is to optimize the computation and update process of the membership functions， effectively reducing the number of iterations and ensuring robust performance even in resource-constrained environments. Finally， in order to achieve more accurate images segmentation， the membership function is corrected by utilizing the local pixel features and spatial relationships within the images. By assigning different weights to the pixels within the neighbourhood， the algorithm better captures the image's details and structural information， resulting in higher segmentation accuracy. This correction strategy considers both the local features of pixels and the spatial relationships between them， ensuring that the segmentation results more closely match the actual content of the images. When a mixed noise density was 10%， the proposed algorithm achieved a segmentation accuracy of 99.72% on the synthetic image dataset and obtained partition coefficient and partition entropy values of 97.23% and 4.61% on the Miao costume patterns dataset. Experimental results show that the proposed algorithm performs well in terms of segmentation accuracy and detail retention ability， and is significantly better than other related algorithms. When faced with noisy and colorful Miao costume patterns datasets， the algorithm accurately identifies and segments different regions within the images while retaining more detailed information.

Keywords：

intuitionistic fuzzy clustering; Miao costume; segmentation; noise; complementary spatial information