基于切断称重法的并条机牵伸区内变速点分布

摘 要：为探究并条机牵伸区内纤维变速点分布的特点，以纺制定重为15.35 g/5m的普梳条和15.03 g/5m的精梳条为例，采用FA320A型高速并条机进行实验，对罗拉牵伸区中的须条进行定长的切断称重得到纤维质量分布，以其纤维质量变化率分布表征变速点分布，并在此基础上借助数据处理的方法分别给出定量表征牵伸区内纤维变速点分布稳定性、集中性、前移性的理论计算公式，并通过并条实验对所给出的公式进行了验证分析。结果表明：该理论计算公式可以判断出变速点分布的位置及状态；在此实验中，精梳条中的纤维在距前罗拉钳口线5～15 mm处变速相对集中且前移、稳定性好；普梳条中的纤维变速点分布较为分散，且远离前罗拉钳口线。该研究为变速点分布理论的发展提供了参考，有助于预测成条质量，提高并条效率。

关键词：并条；变速点；牵伸区；等长切断称重法；质量分布

中图分类号：TS131.9

文献标志码：A

文章编号：1009-265X（2024）10-0094-08

在纺纱系统中，纤维材料经过梳理后，都需要经过并条牵伸［1］加工来改善纤维状态，使弯钩卷曲纤维［2］得以进一步伸直平行，以提高棉条质量。并条机牵伸的过程是一个复杂的纤维运动过程，受到诸多因素的影响，如工艺参数设置、纤维性能及纤维变速点的分布［3］，等等。其中变速点分布与成条质量密切相关［4］，当变速点分布更集中更靠近前罗拉钳口，条子质量更优。因此，研究变速点分布理论对优化生产工艺参数和加强纤维控制有重要意义［5-6］。

许多企业与学者对牵伸区中变速点分布进行了专门的研究，李瑛慧等［7］借助示踪纤维直观观察，并通过测量纤维头端移距研究了纤维变速点；郭明华等［8］采用切断称重法对细纱机牵伸区内浮游纤维变速点分布进行了研究；申元颖［9-10］提出了一种可以动态表征前罗拉钳口线的纤维变速点测试方法，减小了停机和前罗拉钳口线标记的差异性带来的实验误差。除了单纯的实验测试分析，许多学者选用牵伸建模的方式来表达变速点分布，从而实现对变速点的理论分析。Yan等［5］采用力学分析和几何－概率方法对变速点分布进行建模。崔月敏等［11］采用MatLab软件进行建模与仿真模拟，基于循环迭代法计算牵伸区不同压力分布下不同长度纤维的变速点，并得到牵伸区内纤维变速点分布。孙娜等［12］基于牵伸区浮游纤维与其他纤维的接触关系，从力学角度对浮游纤维变速点分布进行动态模拟。这些试验在一定程度上揭示出了变速点分布的实质，但缺少对变速点分布的特点进行定量描述。

本文采用切断称重法来测试变速点分布，以纺制为15.35 g/5m的普梳条和15.03 g/5m的精梳条为例，通过对牵伸区内须条质量分布的测试分析，来研究纤维变速点分布的位置并分别给出定量表征纤维变速点分布稳定性、集中性、前移性的理论计算公式，进而利用理论公式判断和研究牵伸区内精梳条、普梳条纤维变速点的集中位置及分布特点，并通过测试条干性能对比分析其与成条质量的关系。本文对丰富变速点分布理论研究和预测成条质量有着一定的参考意义。

1 变速点分布测试及其理论表达

1.1 纤维变速点分布测试方法

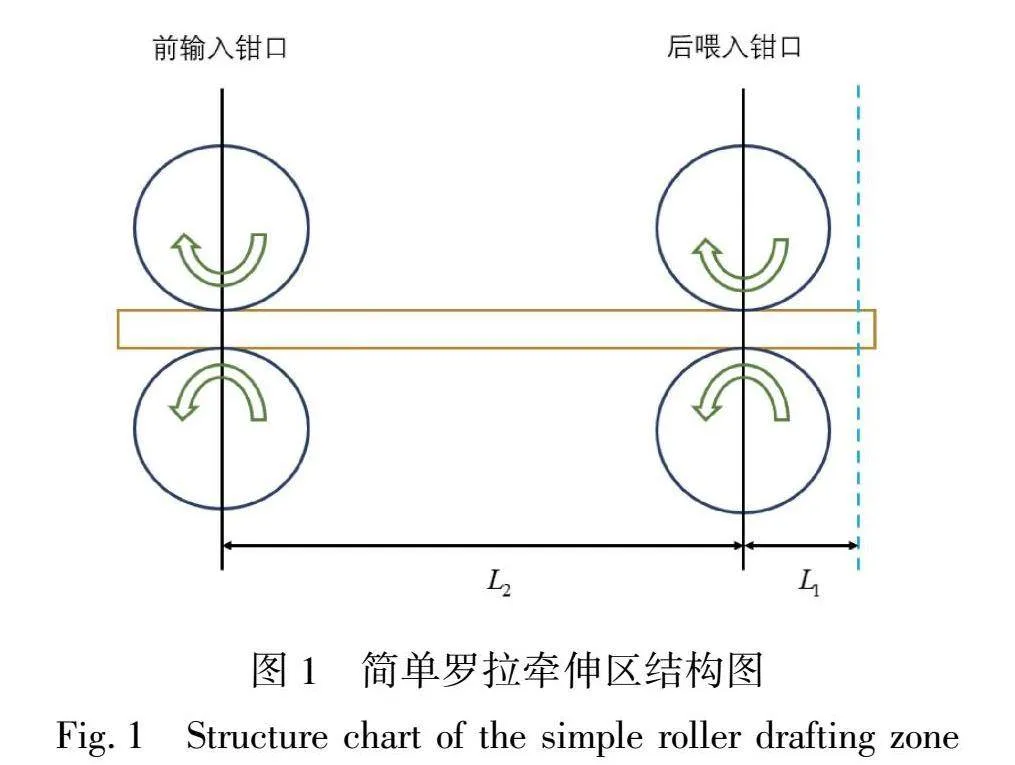
结合牵伸理论和微分无穷分割的思想，采用等长切断称重法测试牵伸区中纤维质量的分布，用纤维质量的变化分布来表征纤维变速点的分布。在并条机高速运转过程中， 紧急制停， 抬起摇架，且在上抬过程中保持牵伸区内的须条处于按压时的状态。简单罗拉牵伸区结构如图1所示。

图1中两对罗拉组成一个牵伸区，上下一对罗拉构成一个钳口，将须条沿着前输出钳口处切断，同时将位于后喂入钳口后部的一定长度L1处的纤维集合体切断，从而得到总长度为L1＋L2的切断称重条，其中L2为后喂入钳口与前输出钳口之间的间距。使获取的切断称重条保持方向不变，并将其转移到提前准备好的方格纸上，取下的须条沿着前输出钳口处按一定长度L3进行切断称重，且设置L2为L3的整数倍，也就是n=L2/L3为自然数，且L1≥L3，完成一共n＋1个重量数据的获取，分别为m m …，mn，mn+ 其中m m …，mn为牵伸区内的由前输出钳口往后喂入钳口方向的须条的重量分布，mn+1为后喂入的纤维集合体的重量，对所获取的称重数据进行逐差计算如式（1）所示：

mn+1-mn=αn（1）

式（1）中的αn为得到n组纤维质量变化值分布，然后分别计算相应的质量变化率如式（2）所示：

βn=αnmn+1（2）

因受牵伸影响纤维质量变化波动大，不能准确反映，故引入质量变化率。式（2）中βn表征牵伸区内由前输出钳口往后喂入钳口之间的且间距为L3的长度内的变速点的分布。

1.2 变速点分布理论表征计算

1.2.1 集中性表征处理

集中性作为评判牵伸区内纤维变速点分布状态的一个指标，其含义比较模糊。在以往的文献里，都是采用“更集中、较集中”对其进行评价分析，缺少一个定量描述。因此，本文引入模糊评价中的最大隶属度有效性原则，对变速点分布的多个集中区域进行等级评价，将变速点分布的模糊性进行量化分析和定量表征，处理步骤如下所示。

计算样本的ωn值，如式（3）所示：

ωn=βn∑ni=1βi（3）

式中：ωn表示各组纤维质量变化率占总的变化率百分比。

计算最大分量和次大分量的百分比的占比，如式（4）—（5）所示，并判断数据集中区。

ηmax=max1≤j≤nωj∑ni=1ωi（4）

ηsec=sec1≤j≤nωj∑ni=1ωi（5）

式（4）、式（5）中的ηmax和ηsec分别是ωn中的最大分量和次大分量占∑ni=1ωi的百分比，易得1/n≤ηmax≤ 0≤ηsec≤1/2。由于在最大隶属原则完全失效时，ηmax=1/n而不为0，所以不宜用ηmax值来直接判断，又由最大隶属度原则的有效性和第二大分量有很大关系，为此引入式（6）—（7）：

γ1=ηmax-1n1-1n（6）

γ2=ηsec-012-0（7）

一般地，γ1值越大最大隶属度原则有效程度越高；而γ2值越大有效度越低，因此可以定义测量有效度的相对指标如式（8）所示：

γ0=γ1γ2（8）

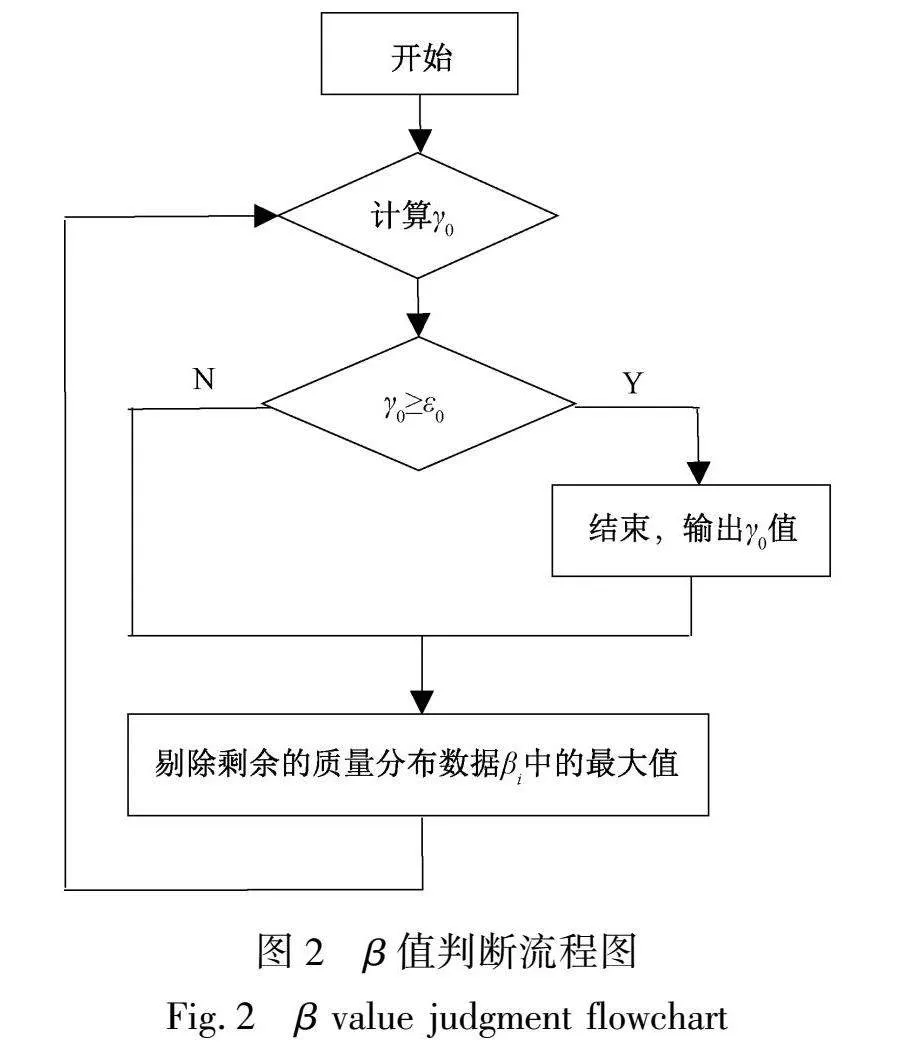
当计算得到的γ0≥ε0时，则表示变速点集中在βmax=max1≤j≤nβj所在的牵伸区的区域内，计算停止，其中0.5≤ε0＜1为所选取的最大隶属度原则有效度指标取值范围；当计算得到的γ0＜ε0时，再按照图2所示进行γ0值的计算的判断，直至计算得到的γ0满足停止条件γ0≥ε0，且设满足停止条件前进行了m次的计算，则有变速点集中在最大的m个βi所在的牵伸区的区域内。

1.2.2 前移性表征处理

根据变速点分布集中性表征处理中计算得到的结果：

当γ0值计算停止时的m＜3且这m个βi中的所有下标数字也满足i＜3时，则满足变速点分布具有前移性；当γ0值计算停止时的m＜3但这m个βi中的至少有一个下标数字满足i≥3时，则表明变速点分布具有集中性，但不具有前移性；当γ0值计算停止时的m≥3时，则表明变速点分布不具有集中性，也就不具有前移性。

1.2.3 稳定性表征处理

保证工艺参数不变的情况下，进行N次测试取样，即共取不同时间的N根的切断称重条进行测试，每次取样获取相应的n＋1个重量数据，从而获取相应的重量数据为mij，其中，i= …， n+ j= …，N，继而计算得到相应的质量差和质量变化率为式（9）—（10）所示：

αnj=mn+1j-mnj（9）

βnj=αnjmn+1j（10）

从而得到相应的变速点质量变化率分布数据βij，其中i= …，n，j= …，N，利用标准差和对数方差表示牵伸区内纤维的变速点分布稳定性，步骤如下所示。

标准差检验：该检验用来表征同种混纺条在不同时间的N根的切断称重条在相同钳口线的变速点稳定性。分别计算每组数据βi1、βi2直至βiN的标准差Si和样本均值i，并在此基础上引出变异系数如式（11）所示：

CVi=SiX-i（11）

当CVi ＜CV0时，则表明该区域内变速点分布稳定，当CVi ≥CV0时，则表明该区域内变速点分布不稳定，其中i= …，n。

对数方差检验：在使用对数方差分析时，该检验用来表征同种混纺条不同钳口线的变速点分布稳定性。首先将每组数据βi1、βi2直至βiN分割平均分成r个子样本，且r≈N每个子样本容量为u，使数据成为βik。其中：i= …，n；j= …， r；k= …，u。然后分别求出每个子样本的均值、方差的对数以及自由度，如式（12）—（14）所示：

βij=∑uk=1βijku（12）

lns2ij=ln∑uk=1βijk-βij2u-1（13）

vij=u-1（14）

式（12）中βijk为第i个样本的第j个子样本中的第k个观察值。βij、s2ij和vij分别代表第i个样本中的第j个子样本的算术均值、方差和自由度，在此基础上作方差分析，并根据F-检验的检验统计量取α值的显著性水平，从附表中查得Fα，若Fs<Fαn- ∑ni=1r-n，则说明这些数据没有显著差别，从而证明了数据的稳定性较好。

2 成条实验

2.1 实验方法和步骤

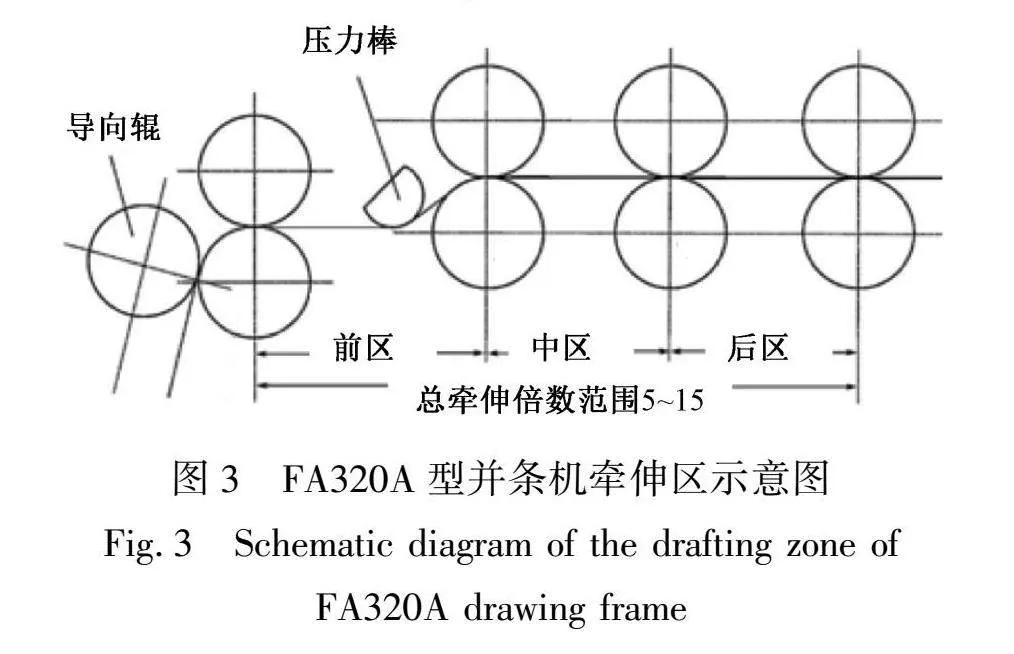
本文采用FA320A型高速并条机（陕西宝成新型纺织机械有限公司）进行实验，其主要参数为：四上四下附导向辊、压力棒式双区曲线牵伸，出条速度250～500 m/min，其牵伸区结构如图3所示。在并条机上设置的工艺参数，具体参数如表1所示。因为采用常规6～9并会使牵伸区棉条过厚，难以精确进行人工切断称重，因此在不影响变速点分布研究的基础上采用四根并合。

为获得牵伸区内纤维变速点分布的表征参数，采用如下步骤测试：

（a）5 mm等长切断称重。将定重为18.64 g/5m的普梳棉条和18.5g/5m精梳棉条在FA320A型高速并条机进行四并分别制成定重为15.35 g/5m和15.03 g/5m的条子。在并条机高速运转过程中，紧急制停，抬起摇架，在牵伸区须条上的前罗拉钳口线位置到压力棒中心后5 mm做标记，从而得到总长度为30 mm的切断称重条。将须条剪断并转移到提前准备好的方格纸上。将取下的须条沿着前罗拉钳口处向后进行5 mm等长切断。

（b）计算得到质量分布表。用精确度为0.0001 g的天平对切断的5 mm须条进行称重并记录数据。

（c）计算得到纤维质量变化率分布。对质量分布进行逐差计算得到纤维质量变化率分布。

（d）用YG133b条干均匀度测试分析仪测试条干性能。

2.2 实验数据处理

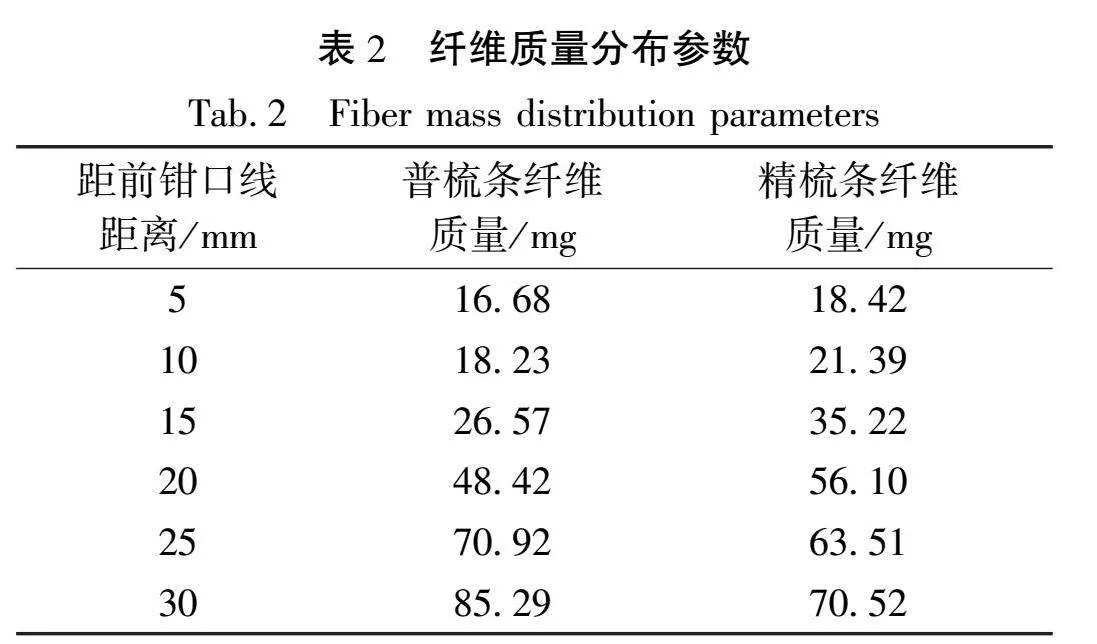
在保证牵伸倍数、隔距等工艺参数相同的基础上，采用切断称重法，寻找纤维变速集中分布区域。利用精梳条和普梳条分别在FA320A型高速并条机上分别进行9次测试取样，即共取不同时间的9根的条子进行切断称重。每次取样获取相应的6个重量数据，求得各个区域的平均值，得到原始数据。纤维的质量分布参数如表2所示。

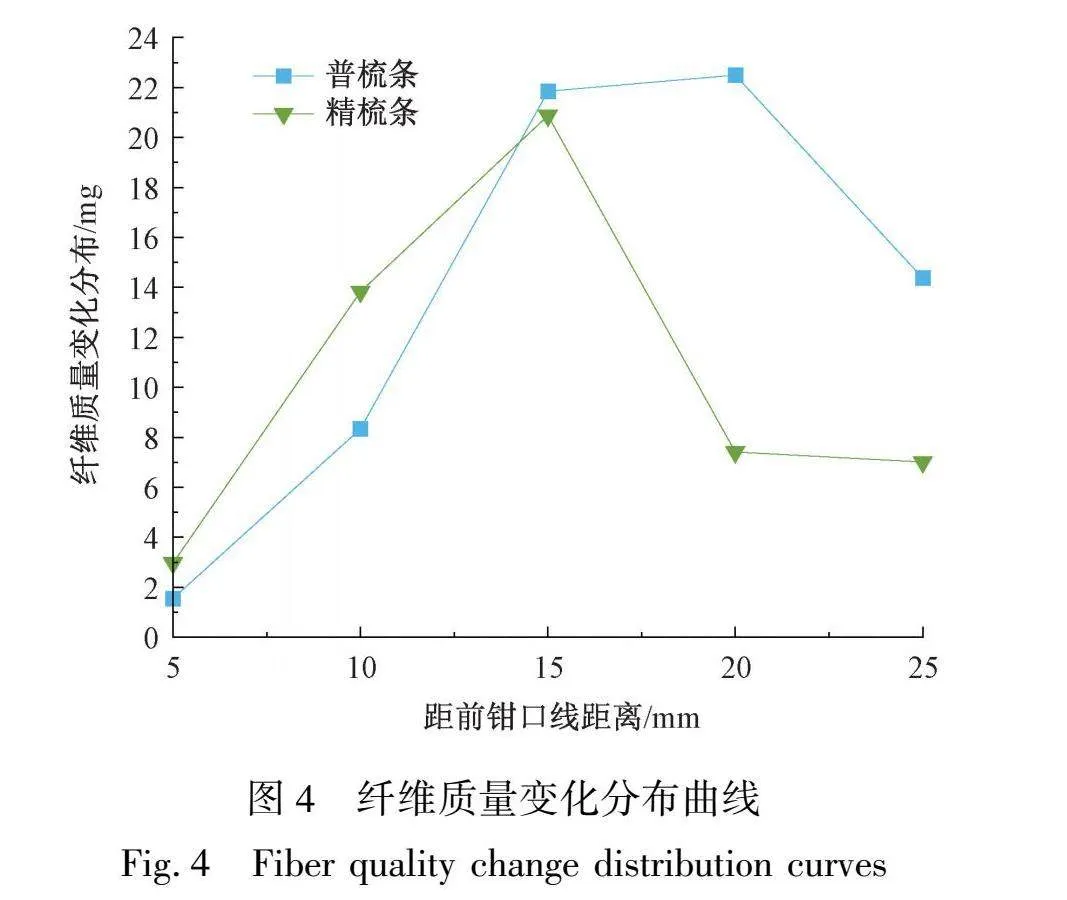
根据式（1）对纤维质量分布进行逐差计算，得到的纤维质量变化分布曲线如图4所示。

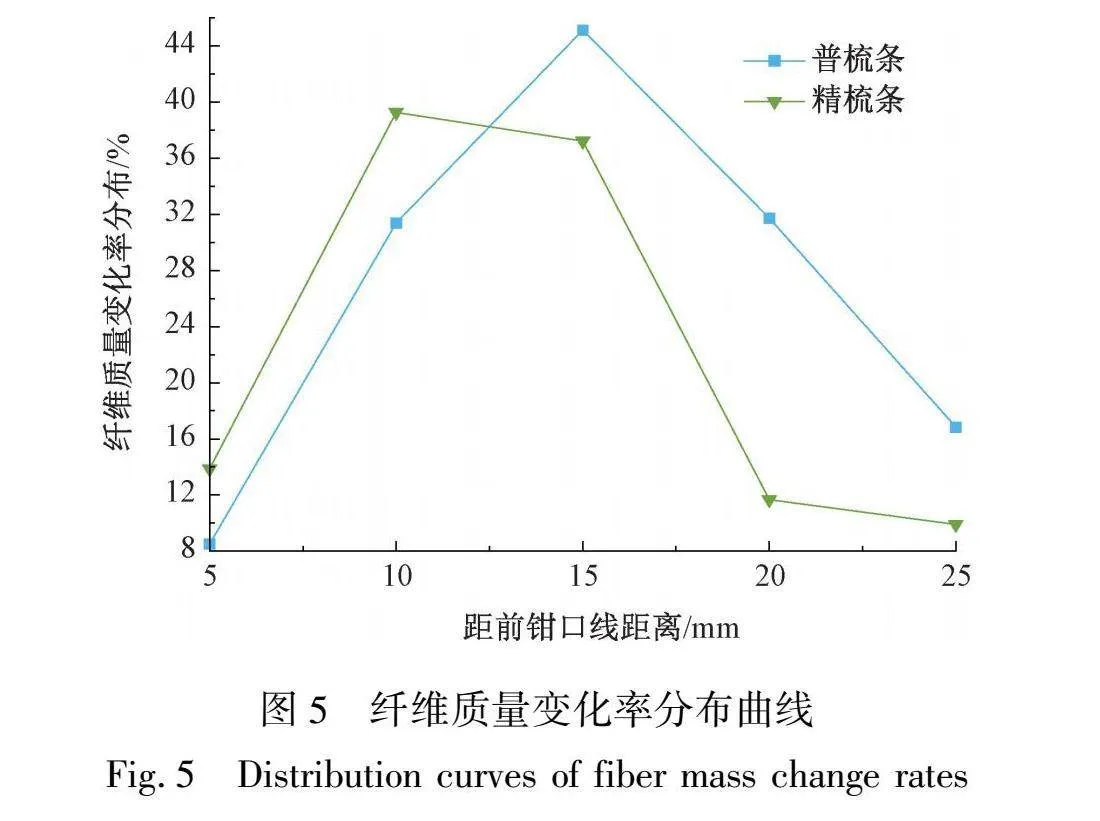
根据式（2）对测量的纤维质量变化分布数据进行计算，得到的纤维质量变化率分布曲线如图5所示。

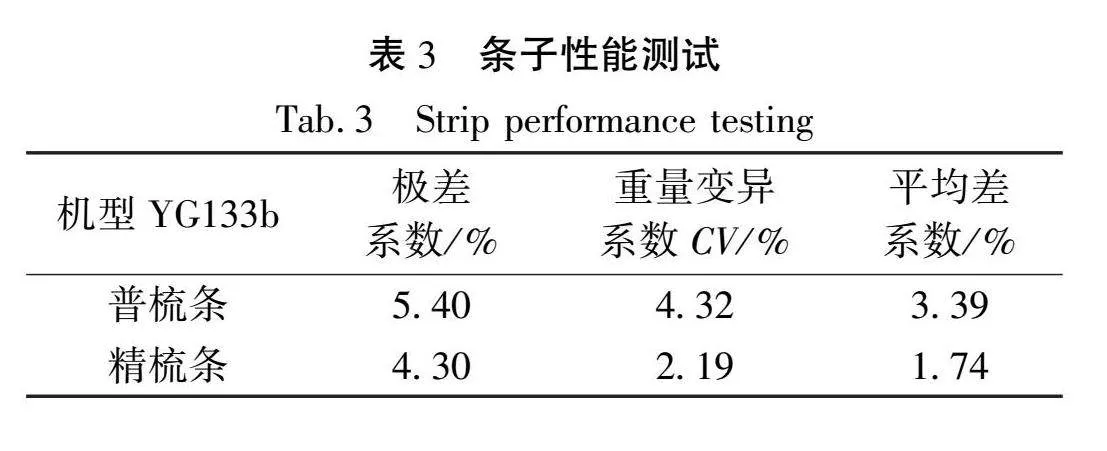
用YG133b条干均匀度测试分析仪测试头并条的条干性能，测试的性能指标如表3所示。

3 结果分析

3.1 集中前移性

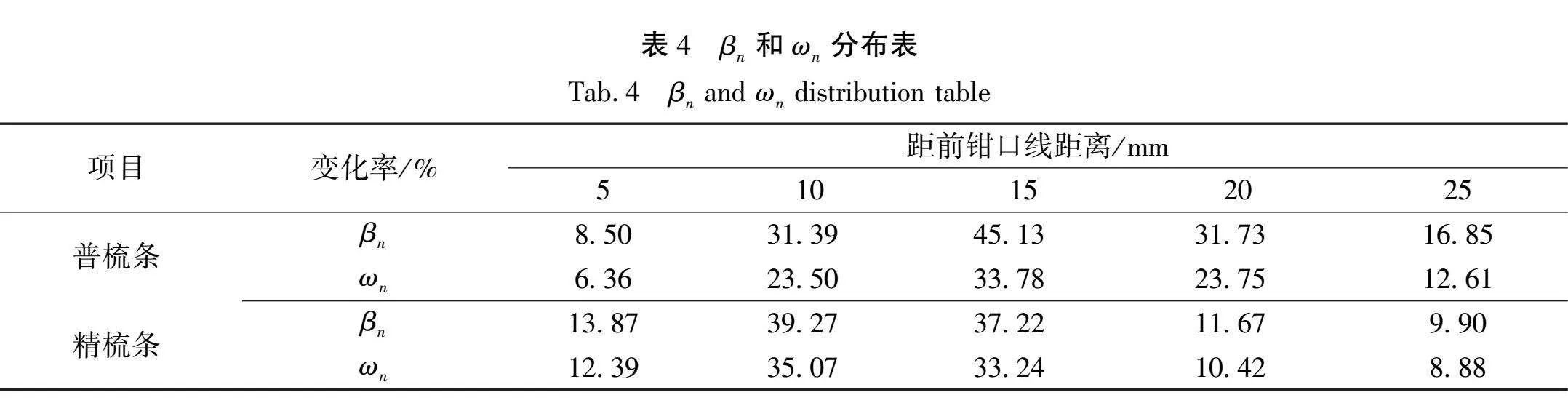
测得的普梳条和精梳条各组纤维质量变化率分布和其对应的各组纤维质量变化率占总的变化率百分比分布如表4所示。

对于普梳条来说，取ε0为0.5，代入集中性表征计算公式，经过计算直至得到γ0=0.56＞0.5。由结果分析可知，普梳条的纤维变速点分布呈现较为分散状态，主要分布在ω2、ω3、ω4这3个区域。根据前移性表征计算得出，变速点分布既不集中也不前移。从表3性能测试可以看出，条子的极差系数偏大，可能是因为纤维头端变速位置有前有后且数量不等导致纤维变速点的相对分散，从而形成移距偏差并造成附加不匀，使成条质量恶化，极差系数偏大。

对于精梳条来说，取ε0为0.5，代入集中性表征计算公式，经过计算直至得到γ0=0.92＞0.5。由结果分析可知，精梳条的纤维变速点分布呈现集中状态，主要集中在ω2、ω3这两个区域，且越靠近前罗拉钳口线，集中程度越大。从表3性能测试可以看出精梳条子的极差系数、重量变异系数和平均差系数控制得都比普梳条好，这是因为精梳后条子伸直度、分离度、平行度得到提升，前、后弯钩纤维得以消除，改善纤维在须条中的排列形态，使成条质量优化。

3.2 稳定性

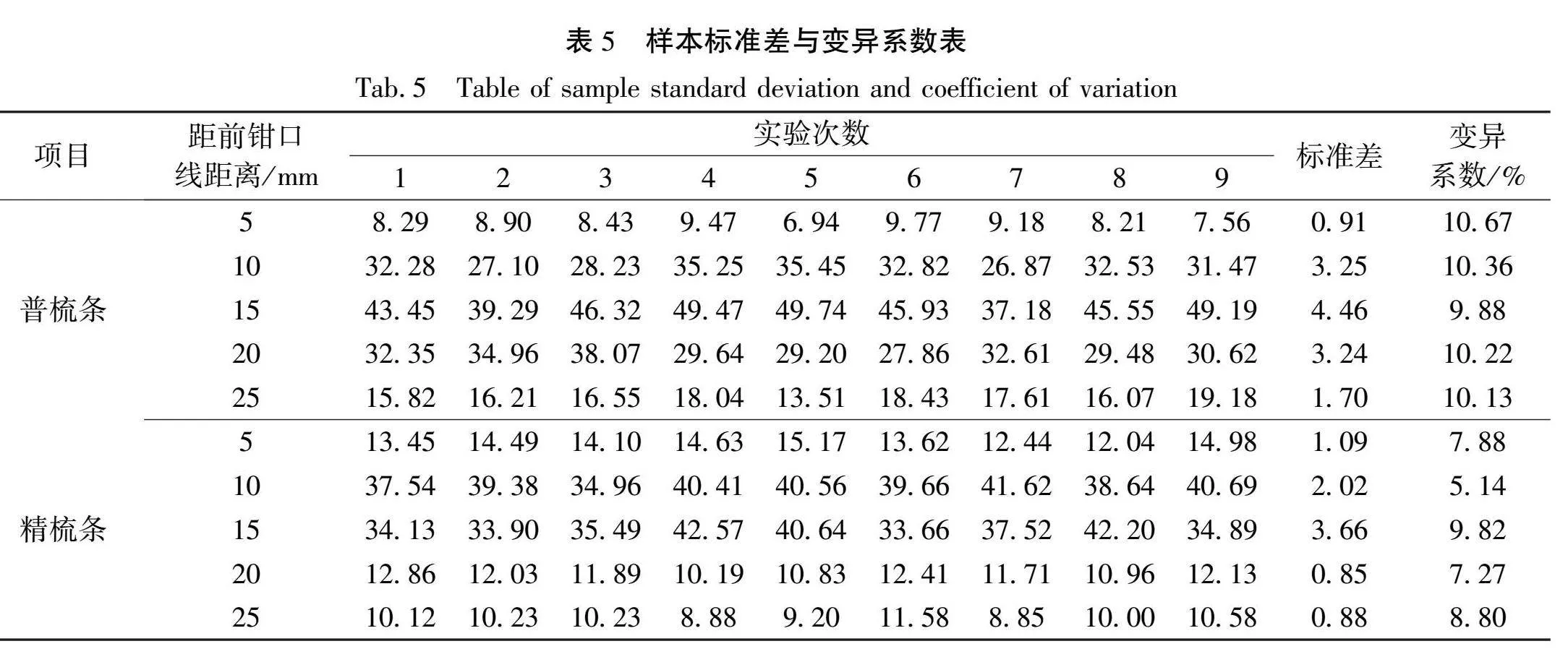
利用定重为18.64 g/5m的普梳棉条和18.5 g/5m的精梳棉条在FA320A型高速并条机上进行9次测试取样，即共取不同时间的9根切断称重条进行测试，每次取样获取相应的6个重量数据，对原始数据进行处理，得到纤维质量变化率分布表。在此基础上进行标准差和变异系数分析计算，所得数值如表5所示。

从表5中可以看出普梳条距前钳口线5 mm时，变异系数最大且小于规定值15%；精梳条距前钳口线20 mm时，变异系数最大且小于规定值15%，说明这两组数据都较为稳定。根据距前钳口线距离不同，将样本分为五组进行对数方差分析，分组结果如表6所示。

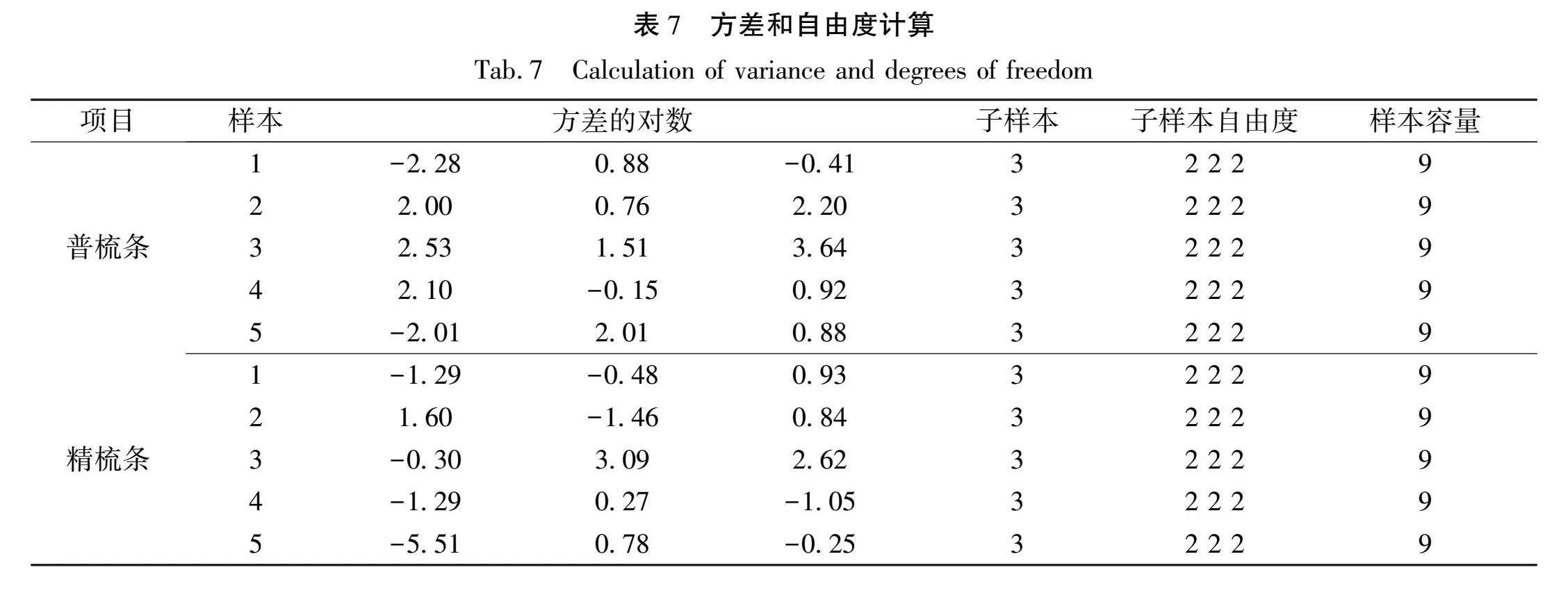
各子样本的方差和自由度计算如表7所示。

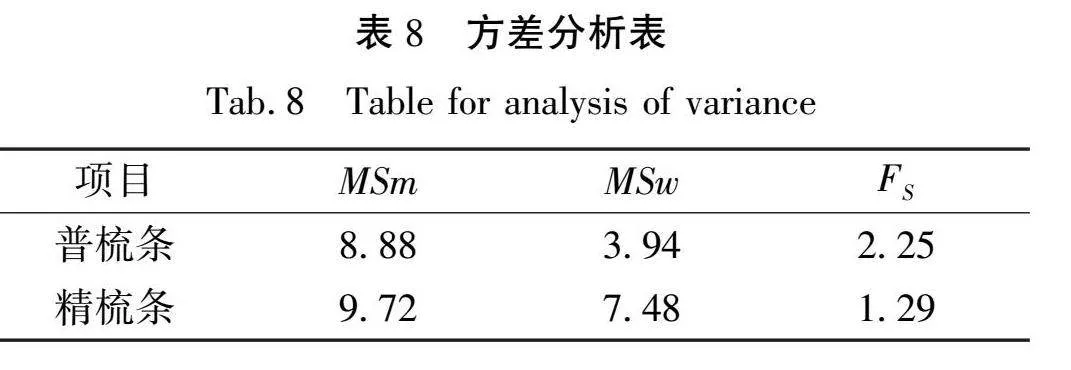
对表7数据作方差分析得到结果如表8所示。

从表8可以看出，普梳条和精梳条的FS值比取0.05时的临界值还要小，即未发现精密度有显著差别，说明这两组数据稳定性较好。从表5及对数方差分析可知，无论是精梳条还是普梳条的变速点稳定性都控制较好，说明纤维所受的引导力和控制力均匀稳定，布置的摩擦力界合理。由表3性能测试可以看出，精梳半熟条的重量变异系数和平均差系数控制比普梳半熟条更加合理，说明条子的重量不匀和片段间不匀率控制得较好，线密度不匀小。因此，为了增进输出棉条的条干均匀度，需要有效控制纤维变速点的稳定性，设置合理的工艺参数以达到良好的效果。

4 结论

本文基于切断称重法在FA320A型高速并条机上对精梳条和普梳条的纤维变速点分布点进行研究，通过数据处理的方法分别给出定量表征牵伸区内纤维变速点分布稳定性、集中性、前移性的理论计算公式，并通过并条实验进行了验证分析，结合条干性能测试，主要得出以下结论：

a）精梳条的变速点分布主要集中在距前罗拉钳口线5～15 mm这段距离中，且具有前移性；普梳条的变速点分布集中在距前罗拉钳口线5～20 mm这段距离中，且变速点分布不前移，但两者的稳定性都控制较好。

b）对比发现精梳条变速点分布的集中位置较普梳条而言提前了5 mm，因此前移性更优，故在一定范围内，纤维变速点分布越集中、前移、稳定，那么它的成条质量越优。在实际生产过程中，要想使条子的条干均匀度更好，就要有效控制纤维运动、设置合理的工艺参数，使变速点分布更集中、稳定、前移。

参考文献：

［1］梁巧敏，崔益怀，张娣，等.基于不同混合工艺的棉/舒弹丝纤维混纺纱性能研究［J］.丝绸，202 59（2）：25-30.

LIANG Qiaomin， CUI Yihuai， ZHANG Di， et al. Study on the properties of cotton/SUSTANS fiber blended yarn based on different blending processes［J］. Journal of Silk， 202 59（2）： 25-30.

［2］SUN N， LIU M. Study on the accelerated-point distribution of floating fibers in the drafting zone［J］. Textile Research Journal， 202 92（17-18）： 3193-3203.

［3］尤沙沙， 全晶， 张瑞云， 等. 环锭细纱网格圈牵伸纤维变速点分布研究［J］.上海纺织科技， 202 49（11）： 6-9.

YOU Shasha， QUAN Jing， ZHANG Ruiyun， et al. Research on the distribution of fiber accelerations of modified lattice apron drafting device［J］. Shanghai Textile Science & Technology， 202 49（11）： 6-9.

［4］郭明华， 刘新金， 朱海荣，等. 前牵伸区内纤维变速点分布对混纺纱成纱质量的影响［J］. 丝绸， 202 58（8）： 28-32.

GUO Minghua， LIU Xinjin， ZHU Hairong， et al. Effect of fiber accelerated-point distribution in the front draft zone on the yarn quality of blended yarns［J］. Journal of Silk， 202 58（8）： 28-32.

［5］YAN G S， YU C W. The influence of fiber length distribution on the accelerated points in drafting： A new perspective on drafting process［J］. Fibers and Polymers， 2009， 10： 217-220.

［6］曲华洋， 谢春萍， 刘新金，等. 超大牵伸条件下前牵伸区内纤维变速点分布对成纱质量的影响［J］. 上海纺织科技，2017， 45（5）：38-41.

QU Huayang， XIE Chunping， LIU Xinjin， et al. Effect of fibers accelerated-point distribution of front draft zone on yarn quality on the super high draft spinning frame［J］. Shanghai Textile Science&Technology， 2017， 45（5）： 38-41.

［7］李瑛慧， 谢春萍， 刘新金. 基于纤维变速点分布实验的成纱条干不匀研究［J］. 纺织学报， 2016， 37（8）： 32-36.

LI Yinghui， XIE Chunping， LIU Xinjin. Study on yarn unevenness based on experiment of fibers accelerated-point distribution［J］. Journal of Textile Research， 2016， 37（8）： 32-36.

［8］郭明华.罗拉牵伸中纤维变速点分布研究［D］. 无锡：江南大学， 2022.

GUO Minghua. Research on the Distribution of Fiber Accelerated Points in Roller Drafting［D］.Wuxi： Jiangnan University， 2022.

［9］申元颖. 牵伸区内纤维运动的研究［D］. 上海：东华大学， 2023.

SHEN Yuanying. Study on Fiber Movement in Drafting Zone［D］. Shanghai：Donghua University， 2023.

［10］SHEN Y， QIAN X， YU C. A study on the dynamic motion of floating fibers in the double apron drafting process［J］. Textile Research Journal， 202 92（13-14）： 2476-2486.

［11］崔月敏， 程隆棣， 和杉杉， 等. 基于循环迭代法的牵伸区纤维运动仿真模拟［J］. 纺织学报， 2023， 44（2）： 76-82.

CUI Yuemin， CHENG Longdi， HE Shanshan， et al. Simulation of fiber motion in drafting zone based on cyclic iterative method［J］. Journal of Textile Research， 2023， 44（2）： 76-82.

［12］孙娜，朱国庆，刘美娜，等.基于牵伸区纤维分布的浮游纤维动态行为模拟［J/OL］.棉纺织技术，2024：1-13［2024-04-17］.http：//kns.cnki.net.elib.zstu.edu.cn：80/kcms/detail/61.1132.TS.20240301.1138.002.html. SUN Na， ZHU Guoqing， LIU Meina， et al. Simulation of dynamic behavior of unequal-length fibers based on fiber distribution in the drafting zone［J/OL］. Cotton Textile Technology， 2024：1-13［2024-04-17］.http：//kns.cnki.net.elib.zstu.edu.cn：80/kcms/detail/61.1132.TS.20240301.1138.002.html.

Distribution of variable speed points in the drafting zone of the drawing

frame based on a cut-weighing method

MA Wenjia， LIU Xinjin

（College of Textile Science and Engineering， Jiangnan University， Wuxi 21412 China）

Abstract：

Drafting is one of the four major mechanical effects in the spinning process， and the quality of the drafting effect directly affects yarn quality. During the roller drafting process， the fibers in the sliver slip with each other at accelerated points， so the distribution if fiber accelerated points has the most significant influence on the yarn quality. So far， plenty of literature has analyzed the qualitative effects of fiber types， drafting methods and drafting multiple on accelerated points， but these studies are all under ideal assumptions， and they have not yet given quantitative test of accelerated points distribution. Furthermore， the unevenness of the yarn after drafting is not only influenced by the differences in accelerated points but also by the drafting multiple. Therefore， the unevenness of the yarn after drafting does not directly reflect the stability of fiber movement.

Therefore， after analyzing the mechanism of roller drafting， this study presented a new method to test the distribution of accelerated points in the roller drafting zone. The slivers were cut at equal lengths and weighed， and then based on the weight change of the slivers in the drafting zone， the distribution of the accelerated points was characterized. On the basis of the data obtained from the test， the theoretical formulae characterizing the stability， concentration， and forward movement of the fiber accelerated points distributions in the drafting zone were derived with the assistance of data processing methods. Under the condition of keeping the process parameters constant， experiments were conducted by using combed and carded slivers as raw materials for blending. Validation analysis was performed on the provided formulas， revealing that the distribution of accelerated points in combed slivers is more concentrated， stable， and forward-moving. Consequently， the quality of the resulting yarn is superior. The more dispersed the accelerated points are in carded slivers， particularly those away from the front nip， the higher their range coefficient will be， leading to greater unevenness in the sliver. Therefore， to improve the evenness of the sliver， it is essential to effectively control fiber movement and set reasonable process parameters to make the distribution of accelerated points more concentrated， stable， and forward-moving.

The present study characterizes the distribution of accelerated points in the drafting zone using the distribution of fiber mass changes. It analyzes the regions where fiber accelerated points are concentrated within the drafting zone， and compares the strip performance to explore the relationship between the distribution of fiber accelerated points and strip quality. The aim is to investigate the laws of fiber speed variations within the drafting zone. It provides a quantitative approach to studying the distribution of fiber accelerated points in roller drafting. The study facilitates the selection of optimal drafting components and the development of optimal drafting processes. This improves sliver performance and yarn quality. On a practical level， the rationality of the drafting process can be judged， and the quality of the slivers in the drawing process can be analyzed and predicted. On a practical level， it is possible to judge the rationality of the drafting process， analyze and predict the quality of the slivers in the drawing process. This has significant economic implications for optimizing drafting process settings and improving drafting efficiency.

Keywords：

drawing; accelerated points; draft zone; equal length cutting weighing method; mass distribution