注重画图能力教学 发展几何直观素养

【摘要】基于学生“自主画图”类问题的案例分析，明确“自主画图”类问题“内容领域”和“命题动因”的两种分类标准，探析“自主画图”类问题“发展学生数学阅读与理解能力、信息提取与转化能力、图形操作与探究能力、结果预测与估计能力、几何直观与想象能力”的教学价值，进而引发“加强画图方法的指导、提供自主画图的机会、发展几何直观的素养”的教学思考.

【关键词】画图能力；几何直观；价值探析；教学思考

1“自主画图”类问题的提出

在一次课堂上，笔者给出这样一个问题[1]：求点P（1，-3）到直线y＝34x+3的距离.不少学生在草稿纸上徒手画出如图1-①所示的图形，于是有PO＝12+32＝10，由S△ABO＝12AO·BO＝12AB·OH求得OH＝125，进而求得PH＝PO+OH＝10+125.

这个过程看似无懈可击，但与PH＝275的正确答案大相径庭.事实上，过点P的垂线并不经过原点O，正确图形如图1-②所示.学生中这样的现象并非个案，都是随意画图惹的祸.目前不少初中生习惯了在现成图形上解答，画图随意性强，动手操作能力不够，缺少图形目测能力、估计能力与几何直观能力，面对没有提供图形而又需要自主画图的问题时往往束手无策，这与当下初中数学教学不无关系.数学课堂上，以课件、投影代替学生自主画图的现象比比皆是；所谓的“导学案”文字、图形应有尽有、面面俱到，学生没有自主画图的空间，失去锻炼自主画图能力的机会.

史宁中先生说直观高于一切.《义务教育数学课程标准（2022年版）》（以下简称《课标（2022年版）》）将“几何直观”[2]列为初中数学素养的九个主要表现之一.图形是几何直观的重要的载体，代数问题有时也需借助几何直观研究，许多数学问题需要学生自主画图探究、分析与思考.因此，自主画图能力是一种不可或缺的数学能力，培养学生自主画图能力、发展学生几何直观素养迫在眉睫.2024年江苏泰州初中数学学业水平考试试卷按照《课标（2022年版）》“以评促学、以评促教”的要求，在考查学生自主画图能力上着墨较多，其中有5道试题需要学生自主画图或补充图形思考，旨在引导数学教学重视培养学生自主画图能力，发展几何直观素养.本文以2024年泰州卷相关试题为案例，谈谈“自主画图”类问题及其分类、价值探析与教学思考.

2“自主画图”类问题及其分类

这里的“自主画图”并非专门的几何作图，也不是几何问题中的添加辅助线，而是数学问题中不提供图形或只提供基础图形（不妨称为“母图”），解题者需要自主画出图形或补充、完善“母图”，借助所画图形进行探究与思考、完成推理与运算.有的问题需要画出精确图形，有的问题只需画出满足条件的示意图.

从内容领域上说，“自主画图”类问题可分为“几何问题自主画图探究”“代数问题图形直观思考”和“数据问题图表直观判断”三个领域.

从条件提供图形的程度上说，“自主画图”类问题可分为两类，一类是“无图”类几何问题，需要解题者完全自主画图进行探究；另一类是提供“母图”类问题，需要补充与完善“母图”，借助图形寻找思路与策略.

从命题动因上说，命制需要自主画图试题既有客观原因，也有主观原因.客观上，一些动态与不确定的数学问题提供图形对解题是一把双刃剑，既便于借助图形理解题意，也可能因为静态图形而导致对思路的误导、思维的干扰，故问题条件中不宜提供图形.主观上，基于命题立意与考查目标而命制“自主画图”类问题，旨在更大程度考查学生直观想象与动态探究能力.

3“自主画图”类问题案例分析

这里主要就“几何问题自主画图探究”和“代数问题图形直观思考”两类问题，对2024年泰州初中数学学业水平考试试卷中“自主画图”类试题进行分析.

3．1几何问题自主画图探究

3．1．1“无图”几何问题

不少几何问题不提供图形，而是通过文字信息表达图形及关系，需要解题者通过阅读文字信息自主画出图形，在所画图形上开展探究与分析、运算与推理活动.

案例1（2024年泰州卷第16题）已知AB是⊙O的直径，点C，D在⊙O上，点C与点A，B不重合，AC＝CD，直线AD交直线BC于点E．若∠BAD＝26°，则∠AEC的度数为°．

该问题的条件均以文字信息的形式给出，图形及相互关系看似不确定，属于客观性“自主画图”类几何问题，正确地画出图形是解决问题的关键.常规思路是依照文字呈现顺序边读题边画图.

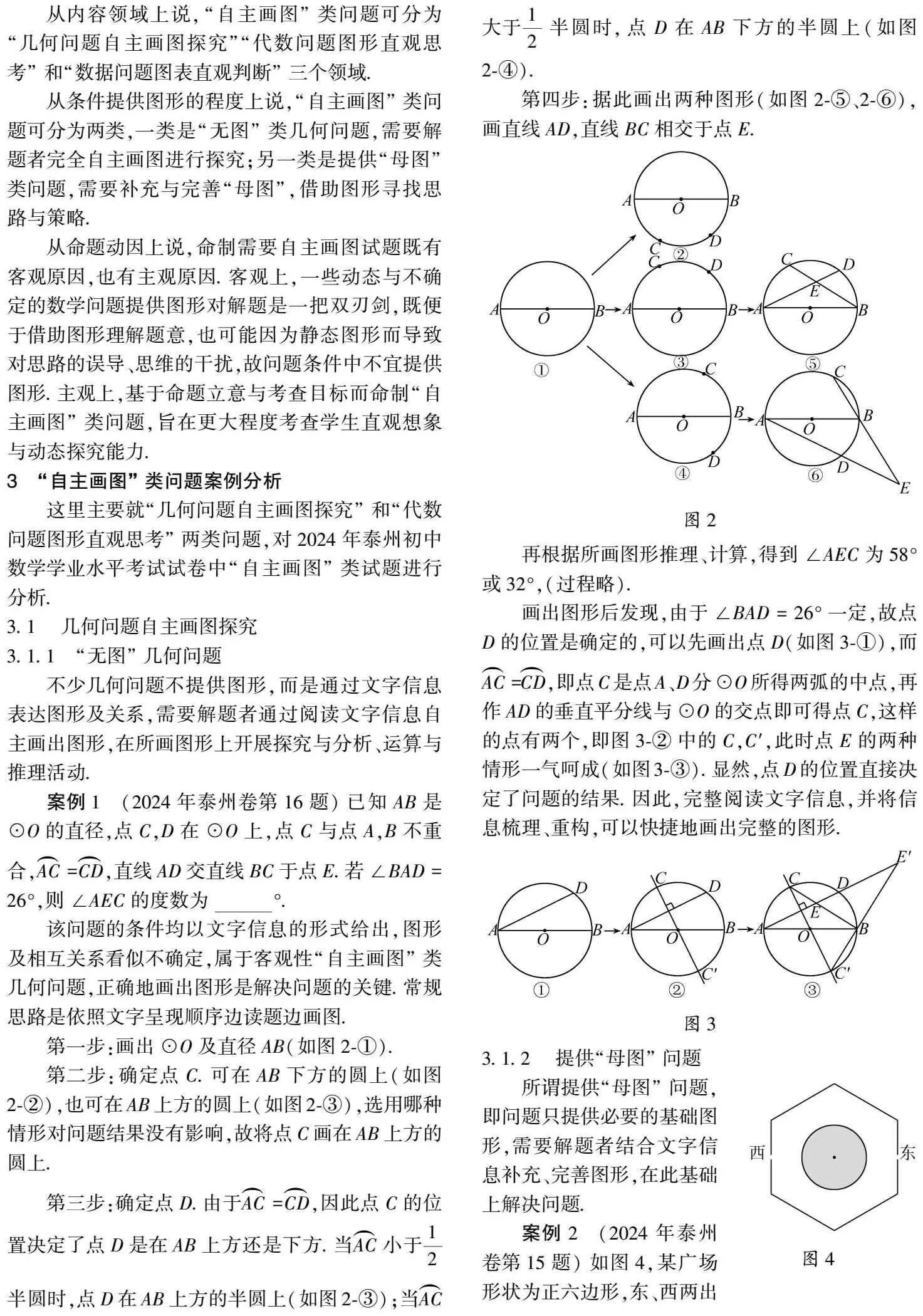
第一步：画出⊙O及直径AB（如图2-①）.

第二步：确定点C.可在AB下方的圆上（如图2-②），也可在AB上方的圆上（如图2-③），选用哪种情形对问题结果没有影响，故将点C画在AB上方的圆上.

第三步：确定点D.由于AC＝CD，因此点C的位置决定了点D是在AB上方还是下方.当AC小于12半圆时，点D在AB上方的半圆上（如图2-③）；当AC大于12半圆时，点D在AB下方的半圆上（如图2-④）.

第四步：据此画出两种图形（如图2-⑤、2-⑥），画直线AD，直线BC相交于点E．

再根据所画图形推理、计算，得到∠AEC为58°或32°，（过程略）.

画出图形后发现，由于∠BAD＝26°一定，故点D的位置是确定的，可以先画出点D（如图3-①），而AC＝CD，即点C是点A、D分⊙O所得两弧的中点，再作AD的垂直平分线与⊙O的交点即可得点C，这样的点有两个，即图3-②中的C，C′，此时点E的两种情形一气呵成（如图3-③）.显然，点D的位置直接决定了问题的结果.因此，完整阅读文字信息，并将信息梳理、重构，可以快捷地画出完整的图形.

3．1．2提供“母图”问题

所谓提供“母图”问题，即问题只提供必要的基础图形，需要解题者结合文字信息补充、完善图形，在此基础上解决问题.

案例2（2024年泰州卷第15题）如图4，某广场形状为正六边形，东、西两出入口位于两边正中（出入口宽度不计），且相距36m，广场中心是直径为18m的圆形水池．游客从东边进、西边出的最短路程是m．

该题提供了“正六边形与圆组合”的“母图”，问题要从三个方面思考：一是怎么画出最短路线，二是为何这样路程最短，三是如何求得最短路程.

第一步：画出最短路线.由生活经验可知：如图5，分别过点A，B作⊙O的切线，切点为C，D.初步判断：线段AC—CD—线段DB是最短路线.

第二步：确认路程最短.假设从A出发到⊙O上的点E，再沿圆周走到F，再走到B处.根据“两点之间线段最短”有：线段AE与ED的长度和大于AC的长，DF与线段FB的长度和大于DB的长，故线段AC—CD—线段DB就是最短路线.

第三步：计算最短路程（答案为3π+183，过程略）.

可以设想：假如试题提供“最短路线”的图形，那留给学生的只有根据定理、公式进行的机械运算，思维含量大为减少，失去了作为“亚压轴”填空题的价值.经了解学生发现，问题的难点恰恰就在“最短路线”的确定上.如果教师真正引导学生亲历“从A走到B”的过程，积累生活与数学活动经验，学生对这样的问题时还会束手无策吗？

3．1．3几何动态探究问题

一些几何动态问题难以或者不能给出完整图形，否则可能因为所给图形不完备而误导学生的思维，只能由解题者自主补充、完善图形动态探究.

案例3（2024年泰州卷第26题）已知：△ABC中，AB＝AC，点D，E分别在AB，AC边上，点A关于DE的对称点P落在BC边上，且DP⊥BC．

（1）（2）略.

（3）若AB＝6cm，将△DEP绕点E逆时针旋转90°后得到△D′EP′．当△D′EP′的一边恰好落在△ABC一边所在的直线上时，求△ABC的面积（图6-③供选用）．

解决“已知腰长求等腰三角形面积”的问题有两种思路：一是求出某一内角的度数，二是求出底边的长.究竟选用哪种思路，要结合其他条件思考.条件“△D′EP′的一边恰好落在△ABC一边所在的直线上”，要分“D′P′落在直线BC上”“EP落在直线AC上”和“ED落在直线AC上”三种情况讨论，并在“母图”上分别画出满足条件的图形进行探究.

Ⅰ.若D′P′落在直线BC上（如图7-①）.由旋转知：EP′＝EP，∠PEP′＝90°，有∠EPP′＝45°，进而∠A＝∠EPP′＝45°.

Ⅱ.若EP落在直线AC上（如图7-②）.由旋转知：D′P′⊥DP，而DP⊥BC，所以D′P′∥BC，从而∠P′＝∠ACB，即BC＝BA，而AB＝AC，所以△ABC为等边三角形，故∠A＝60°.

Ⅲ.经探究发现：ED不可能落在直线AC上.

据此求出△ABC的面积为92或93.

该问题虽然提供了“母图”，但该“母图”的形状并不确定，研究方向也不确定，需要根据后续条件，画出△DEP绕点E旋转得到的△D′EP′后，探究出线段关系与角的关系，逐步明确研究方向是“求∠A的度数”.

3．2代数问题图形直观思考

许多代数问题除了代数方法外，有时转化为图形问题，会使问题更加直观、方向更加清晰.此类问题分为三类，一类是纯代数问题构造图形思考，一类是函数问题结合图象思考，还有一类是代数问题融入几何元素.这里主要讨论后两类问题.

3．2．1函数问题借助图象思考

图象是研究函数问题的重要载体，函数问题可以用纯代数方法解决，但利用图象几何直观解决问题会达到事半功倍的效果.

案例4（2024年泰州卷第6题）一次函数y＝kx+b（k，b为常数，k≠0）的图象与二次函数y＝a（x-1）（x-2）（a为常数，a≠0）的图象有两个交点．设这两交点的横坐标分别为x1，x2，下列结论不正确的是（）.

A．若a>0，k>0，则x1+x2>3

B．若a>0，k<0，则x1+x2<4

C．若a<0，k>0，则x1+x2<5

D．若a<0，k<0，则x1+x2>6

运用纯代数方法，将y＝kx+b代入y＝a（x-1）（x-2）得：ax2-（3a+k）x+2a-b＝0，所以x1+x2＝3+ka.显然，当a，k同号时，x1+x2＞3，但不能保证x1+x2＞6，故A选项正确，D选项不正确；当a，k异号时，x1+x2＜3，一定满足x1+x2<4和x1+x2<5，BC选项正确.

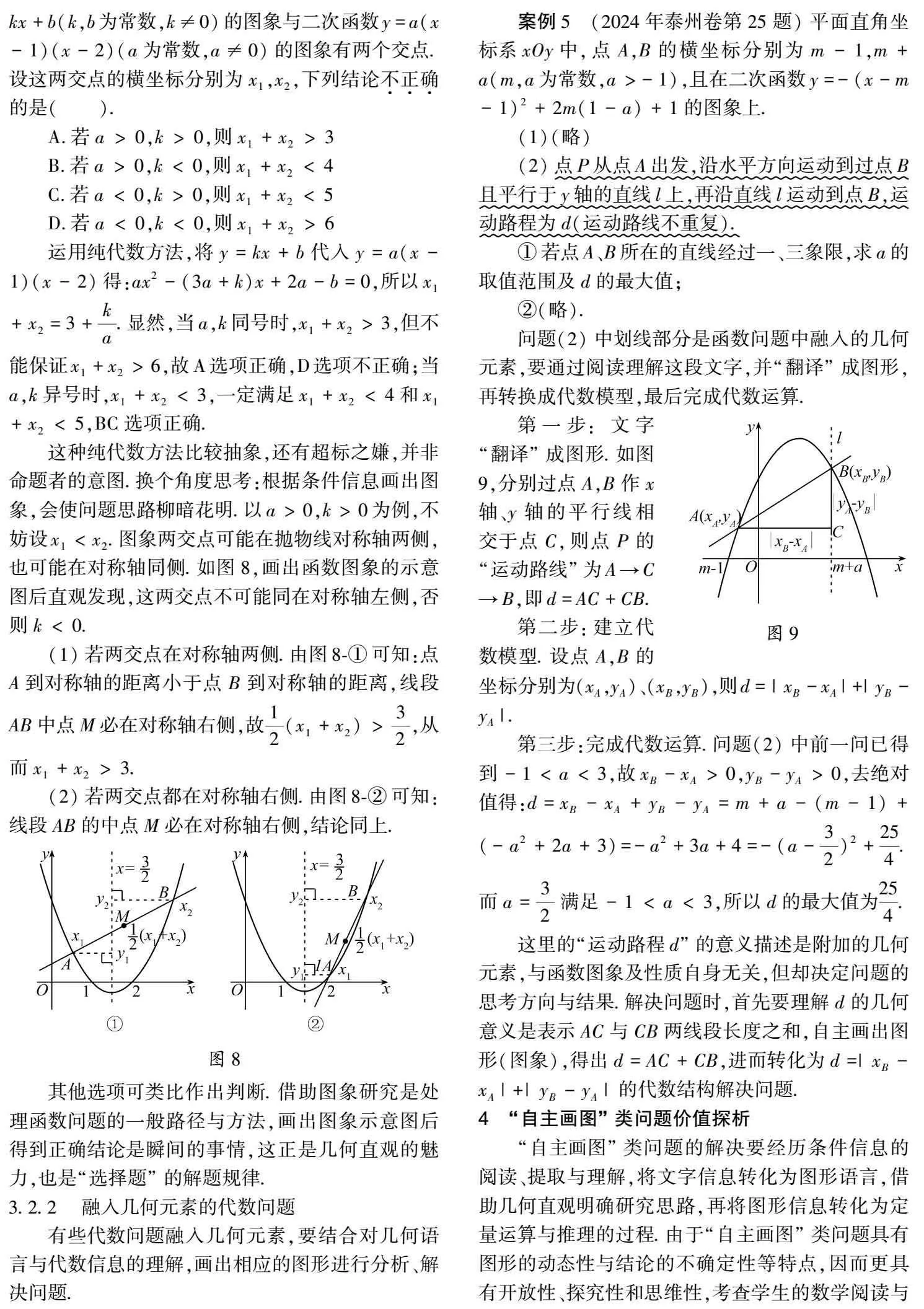
这种纯代数方法比较抽象，还有超标之嫌，并非命题者的意图.换个角度思考：根据条件信息画出图象，会使问题思路柳暗花明.以a>0，k>0为例，不妨设x1＜x2.图象两交点可能在抛物线对称轴两侧，也可能在对称轴同侧.如图8，画出函数图象的示意图后直观发现，这两交点不可能同在对称轴左侧，否则k＜0.

（1）若两交点在对称轴两侧.由图8-①可知：点A到对称轴的距离小于点B到对称轴的距离，线段AB中点M必在对称轴右侧，故12（x1+x2）＞32，从而x1+x2>3.

（2）若两交点都在对称轴右侧.由图8-②可知：线段AB的中点M必在对称轴右侧，结论同上.

其他选项可类比作出判断.借助图象研究是处理函数问题的一般路径与方法，画出图象示意图后得到正确结论是瞬间的事情，这正是几何直观的魅力，也是“选择题”的解题规律.

3．2．2融入几何元素的代数问题

有些代数问题融入几何元素，要结合对几何语言与代数信息的理解，画出相应的图形进行分析、解决问题.

案例5（2024年泰州卷第25题）平面直角坐标系xOy中，点A，B的横坐标分别为m-1，m+a（m，a为常数，a＞-1），且在二次函数y＝-（x-m-1）2+2m（1-a）+1的图象上．

（1）（略）

（2）点P从点A出发，沿水平方向运动到过点B且平行于y轴的直线l上，再沿直线l运动到点B，运动路程为d（运动路线不重复）．

①若点A、B所在的直线经过一、三象限，求a的取值范围及d的最大值；

②（略）.

问题（2）中划线部分是函数问题中融入的几何元素，要通过阅读理解这段文字，并“翻译”成图形，再转换成代数模型，最后完成代数运算.

第一步：文字“翻译”成图形.如图9，分别过点A，B作x轴、y轴的平行线相交于点C，则点P的“运动路线”为A→C→B，即d＝AC+CB.

第二步：建立代数模型.设点A，B的坐标分别为（xA，yA）、（xB，yB），则d＝|xB-xA|+|yB-yA|.

第三步：完成代数运算.问题（2）中前一问已得到-1＜a＜3，故xB-xA＞0，yB-yA＞0，去绝对值得：d＝xB-xA+yB-yA＝m+a-（m-1）+（-a2+2a+3）＝-a2+3a+4＝-（a-32）2+254.而a＝32满足-1＜a＜3，所以d的最大值为254．

这里的“运动路程d”的意义描述是附加的几何元素，与函数图象及性质自身无关，但却决定问题的思考方向与结果.解决问题时，首先要理解d的几何意义是表示AC与CB两线段长度之和，自主画出图形（图象），得出d＝AC+CB，进而转化为d＝|xB-xA|+|yB-yA|的代数结构解决问题.

4“自主画图”类问题价值探析

“自主画图”类问题的解决要经历条件信息的阅读、提取与理解，将文字信息转化为图形语言，借助几何直观明确研究思路，再将图形信息转化为定量运算与推理的过程.由于“自主画图”类问题具有图形的动态性与结论的不确定性等特点，因而更具有开放性、探究性和思维性，考查学生的数学阅读与理解能力、信息提取与转化能力、图形操作与探究能力、结果预测与估计能力、几何直观与想象能力，这正是“自主画图”类问题的价值所在.

4．1数学阅读与理解能力

一般说来，自主画出图形或补充、完善图形的数学问题的条件大多以文字信息为主，解决问题时需要在阅读理解文字信息的基础上画出或补充图形.如案例1要先阅读文字，并按文字呈现顺序逐步画出图形.完整阅读与画图后才发现：原来点D是确定的，只要先确定点D，则AD的垂直平分线与⊙O两个交点就是满足条件的点C，两种情形一步到位.再如案例3的文字信息“△D′EP′的一边恰好落在△ABC一边所在的直线上”意味着需要分类讨论，找出可能的情形、排除不可能的情形.又如案例5要通过对划线部分文字的阅读与理解，自主画出符合条件的图形，从而得出“d就是AC与CB的长度和”的结论，进而转化为A、B两点横坐标差与纵坐标差的绝对值之和，再进行代数运算.另外，还需要理解为什么要加上“运动路线不重复”的限制？如果没有这个限制，点P可在A—C—B间往复运动，此时d就不存在最大值.这足以说明，“自主画图”类数学问题有效考查了文字信息的阅读与理解能力.

4．2信息提取与转化能力

“自主画图”类问题的阅读与理解，旨在提取与转化信息，将文字信息转化为图形（图象）信息，以便探究、分析、解决问题，这是解决“自主画图”类问题的重要策略，比如函数问题借助图象研究是分析与解决问题的一般路径与方法.事实上，案例4的问题解决可以用纯代数方法解决，但将文字信息转化为图象信息，通过直观就能快速作出判断，避免了繁琐的代数运算.再如案例5中，需要阅读并理解条件中d的意义的语言描述，并转化为d＝AC+CB的图形结构，再转化为d＝|xB-xA|+|yB-yA|的代数结构.

4．3图形操作与探究能力

“自主画图”类问题可以考查动手操作与动态探究能力.如案例1没有提供图形，首先要在阅读文字信息的基础上，根据条件的呈现顺序画出图形，由于点C的位置“看似”不确定，而AC＝CD，故点D的位置也“不确定”，从而可能导致结果不唯一.经过尝试画图发现，由于∠BAD＝26°，故可直接确定点D，可谓“众里寻他千百度，蓦然回首，那人却在，灯火阑珊处”.换言之，图3是经过尝试、探究与反思的结果，从条件得到∠AEC的度数或得到图3的思路，都经历了阅读与思考、操作与探究、分析与判断的思维过程.

4．4结果预测与估计能力

由于“自主画图”类问题中图形及相互关系未知或不确定，需要对图形的形状与大小、图形结构与位置关系的变化、问题发展方向与结果具有预测与估计能力.案例2中“正六边形广场”问题，要基于生活经验预测“最短路线”.案例3则要估计到：△DEP按要求旋转到△D′EP′时，只有△ABC满足特定要求（如∠A＝45°或60°）时，才能使△D′EP′的一边恰好落在△ABC一边所在的直线上.再如案例4中，当a＞0，k＞0时，如果只考虑图象两交点在抛物线对称轴两侧的情形（如图8-①），而忽视了两交点在抛物线对称轴同侧的情形（如图8-②），那么这种预见性的缺失可能导致问题结果出现致命性的错误.

4．5几何直观与想象能力

几何问题主要研究图形特征、位置关系与数量关系、运动规律与变化趋势，其研究过程始于几何直观与想象，终于逻辑推理与运算.代数问题尤其是函数问题也应结合图形与图象直观开展研究，以达到“以形助数”“以形释数”的目的.如案例5中的3个问题都需要结合函数图象，通过直观发现结论、代数运算与推理说明结论.问题（1）中，由于m＝-1时，y＝-x2+2a-1，而二次项系数小于0，故图象开口向下.画出图象发现，只有在对称轴（即y轴）右侧时y随x的增大而减小，故x＞0；第（2）问要画出图象，根据对称性和增减性直观得到-1＜a＜3.

5“自主画图”类问题教学思考

自主画图是一种能力，也是一种习惯.从上述案例分析与价值探析可以看出：学生的自主画图能力不可或缺.数学教学要从提升数学素养的高度，重视学生自主画图能力的培养，加强自主画图方法的指导，给学生提供更多自主画图的机会，在自主画图中发展几何直观素养.

5．1加强画图方法的指导

数学教学要培养学生“由文思图”“由数想形”的直观化思考的习惯，准确的图形有助于几何直观.如特殊角要“一画准”，可要求学生借助三角形、量角器、圆规等工具画图，即使是徒手画图也要尽可能准确，条件中的“非标准”图形要尝试标准化处理；对于复杂或动态图形，即使问题提供了图形，也应让学生通过阅读条件并参考所给图形重新画出图形，将所画图形与所给图形比较，如果画出的图形与所给图形有差异，有的可能是由动态图形的不确定性所致，有的可能是由题意理解偏差引起的，从而加深对问题条件、结论的正确理解.纯代数问题在缺少思路时可以考虑能否画出图形（图象）直观地寻找问题解决的方向与思路.由于自主画图的目的是帮助问题解决，所以该精准时精准，该“大致”时“大致”.如案例4中的示意图就在“精准”与“大致”之间：抛物线的开口方向和与x轴两交点（1，0）、（2，0）确定就应该精准，而抛物线的开口大小、直线y＝kx+b的倾斜程度则是大致的.有时还需要根据图形变化趋势与结果的可能性及时调整与优化.如案例1和案例3就需要在画图时作出预判，一边画图一边调整与优化.

5．2提供自主画图的机会

有数学教育专家建议，数学试卷上可少提供图形，尽可能让学生自主画图.诚然，一份试卷提供图形的程度与试题本身特点、试卷版面要求有关，也与命题者对考生阅读与思维的预期有关.但专家的建议至少说明：作为数学教师要有培养学生自主画图能力的意识，课堂上尽可能给学生提供自主画图的机会，不要以课件和现成图形完全代替学生画图.有时可一边引导学生阅读条件一边教师画图示范；有时可放手让学生尝试画图，再组织学生对所画图形进行比较、交流，在“试错”中加深对问题的理解.课堂上的导学单或学历案要适当留白，如只给出条件与目标信息，不提供图形或只提供“母图”，让学生自主画图或补充图形.作业形式要丰富多样，既有提供图形的作业，也有无图或提供“母图”的作业，以培养学生的自主画图能力.

5．3发展几何直观的素养

几何直观与空间观念、模型观念、推理能力、运算能力是相生相伴的，培养学生自主画图能力是提升学生几何直观素养的重要手段.如由图形特征可以直观想象到相应的数学模型，而直观的模型正确与否要通过推理与运算证实或证伪，这就需要推理能力与运算能力.数学模型、数学推理又反过来作用于几何直观素养的发展.建立数与形的联系、借助几何直观使抽象问题形象化、构建直观模型使复杂问题简单化，是落实直观想象素养的几个关键环节[3-4].因此，数学教学要处理好直观、想象、模型、推理的关系.

5．3．1处理好直观与想象的关系

直观想象不仅是一种解决数学问题的方法与技能，也是一种思维习惯与思维方式[3].几何直观是具体的，如由具体的图形直观得到性质、作出判断，但比直观更高层次的思维是想象，数学甚至许多科学发明是从想象开始的.数学教学要将直观与想象有机结合，既要引导学生借助直观思考问题、发现结论，也应适当指导学生经历想象过程，提出数学问题、发现并探索结论.

5．3．2处理好直观与模型的关系

学习者从研究直观对象到储存在大脑中的“模型”，如教材中的定理、公式、法则与运算律等，这些模型基于学生已有的生活经验和数学认知.如案例2中，小学生也知道沿最短路线从一个出入口走到另一个出入口，他们不一定会说明为什么这样走路程最短，靠的生活经验与直观，而不是相应的数学知识.数学教学要处理好直观与模型的关系，引导学生经历数学模型的建构与优化过程，实现从几何直观到数学建模的转化.

5．3．3处理好直观与推理的关系

直观想象不是凭空想象、空穴来风，它需要建立在“数”与“形”的联系基础上，利用几何图形描述问题、借助几何直观理解问题、运用空间想象认识事物的思维过程[6].直观的结论不一定正确，需要通过推理、运算来证实或证伪.“自主画图”类问题研究的一般路径与方法是：自主画出图形→直观发现结论→推理验证结论.数学教学时应将几何直观、数学建模与数学推理作为一个有机的整体，发展学生基于几何直观的抽象能力、模型观念与推理能力等数学素养.

参考文献

[1]钱德春．强化画图意识提升画图能力助力问题解决[J]．中学数学杂志，2021（08）：37-41.

[2]中华人民共和国教育部．义务教育数学课程标准：2022年版[M]．北京：北京师范大学出版社，2022：7.

[3]孔凡哲，史宁中．关于几何直观的含义与表现形式[J]．课程·教材·教法，2012，32（07）：92-97.

[4]周德明，王华民．借助几何直观理解问题，构建直观模型解决问题：浅谈学生直观想象素养的培养[J]．高中数学教与学，2019（05）：15-19.

[5]李昌官．直观想象及其教学[J]．中国数学教育：高中版，2022（03）：3.

[6]朱敏龙．核心素养下数学教学中的六个“不等式”[J]．中学数学杂志，2018（10）：1-4.

作者简介

钱德春（1963—），男，江苏泰州人，泰州市教研室数学教研员，中小学正高级教师;主要从事初中数学教学与命题、教师专业发展等研究.

秦亚丽（1981—），女，江苏泰州人，中学一级教师;主要从事初中数学教学与命题研究.