挖掘好题价值收获以少胜多

【摘要】通过对一道“好题”解法和试题开放性探究，发掘试题潜在教学价值，避免陷入“题海”教学误区，增强学生兴趣引领下的数学学习幸福感，提升学生数学核心素养。

【关键词】开发好题;发掘价值;好奇心;幸福感;核心素养

所谓好题是具有开放性和研究价值的问题.教学中不是缺乏好题，而是缺乏发现好题的眼光，导致学生陷于题海之中， 造成课业负担过重，解题视野狭窄，严重桎梏了学生们的思维空间.多视角、多角度挖掘好题潜在教学价值，灵活应用，以一变十，提升学生数学核心素养，收到事半功倍的功效[1].

试题呈现

如图1，在正方形ABCD中，点E，F在射线BC上，∠EAF=45°，求BEEF的最大值.（2024年成都青羊区中考模拟试题）

试题条件简洁，但指向不明确，问题典型，但两者之间联系“松散”，增强了开发性探究问题的思维空间.

1多解活思路

解法多样性是课程标准理念，在教学中需要教师给予开发和利用.

1.1几何解法

解法1利用一线三直角+隐圆

如图1，过点E作EG⊥AE交AF于点G，过点G作GP⊥EF于点P，则∠B=∠EPG=90°，

因为∠EAF=∠AGE=45°，所以AE=EG，

因为∠BAE+∠AEB=90°，∠GEP+∠AEB=90°，

所以∠BAE=∠GEP，

所以△ABE≌△EPG（AAS），所以GP=BE.

作△EFG的外接圆，设圆心为O，连接OE，OF，OG，则OE=OF=OG，因为∠EGF=135°，所以∠EOF=90°.所以△EFO为等腰直角三角形.

过点O作OQ⊥EF于点Q，则GP+OQ≤OG，所以GP≤OG－OQ，即BE≤OG－OQ，当P，Q位于OG上时取等号.

设OQ=EQ=FQ=a，则OG=OE=2a，EF=2EQ=2a，所以BE≤2a－a，所以BEEF≤2a－a2a=2－12，故BEEF的最大值为2－12.

解法2利用平行构造相似+隐圆

如图2，作正方形ABCD的外接圆，连接AC并取中点O为圆心，延长AE交⊙O于点G，过G作GH⊥BC于点H，则AB∥GH.

所以△ABE∽△GHE，所以EGAE=GHAB.（1）

连接BG，由于∠BGE=∠ACB=∠EAF=45°，

又∠BEG=∠AEF，

所以△BEG∽△FEA，所以BEEF=EGAE. （2）

将（1）式代入（2）式，得BEEF=GHAB，

由于AB大小一定，只需GH最大.

过O作OP⊥BC于点P，并延长交⊙O于点Q，

所以GH≤PQ，当GH重合于PQ时取等号.

设AB=BC=2a，则AC=22a，所以OQ=OC=2a，

易得OP为△ABC的中位线，所以OP=12AB=a，

所以PQ=OQ－OP=2a－a.

所以BEEF=GHAB≤PQAB=2a－a2a=2－12，

故BEEF的最大值为2－12.

1.2代数解法

解法3如图3，连接AC，在正方形ABCD中，∠ACE=∠EAF=45°，又∠AEC=∠FEA，所以△ACE∽△FAE，

+HodReU3zQ2ipfwrFC4e3XicRdHOzVeaMNez6/Te+fA=所以AEEC=EFAE，即AE2=EC·EF.

设正方形ABCD的边长为1，BE=x（0＜x＜1），

在Rt△ABE中，AE2=AB2+BE2=1+x2，

所以EF=AE2EC=1+x21－x.

设BEEF=x（1－x）1+x2=k（k＞0），整理，得

（k+1）x2－x+k=0，

由判别式得Δ≥0，所以（－1）2－4k（k+1）≥0，

整理，得（2k+1）2≤2，解得k≤2－12（另解已舍）.

即BEEF≤2－12，故BEEF的最大值为2－12.

思考1还有其它解法吗？答案是肯定的，请大家自行探讨.

2多变提能力

任何事物变化是绝对的，静止是相对的.探讨对问题在不同条件下的解答和结果成立性，会激发人们的好奇心，提升认识问题和解决问题的能力.

2.1改变数据

例1如图4，在正方形ABCD中，点E，F在射线BC上，∠EAF=60°，求BEEF的最大值.

解如图4，过点E作EG⊥AE交AF于点G，过点G作GP⊥EF于点P，则∠B=∠AEG=∠EPG=90°.

因为∠EAF=60°，所以EG=3AE.

因为∠BAE+∠AEB=90°，∠GEP+∠AEB=90°，

所以∠BAE=∠GEP，

所以△ABE∽△EPG，

所以GPBE=EGAE=3，GP=3BE.

作△EFG的外接圆，设圆心为O，连接OE，OF，OG，则OE=OF=OG，

因为∠EGF=∠EAF+∠AEG=150°，所以∠EOF=60°.

所以△EFO为等边三角形.

过点O作OQ⊥EF于点Q，

则GP+OQ≤OG，所以GP≤OG－OQ，当P，Q位于OG上时取等号.

设OE=EF=2a，则OG=OE=2a，于是OQ=3a，GP≤2a－3a，

所以BEEF=GP3EF≤2a－3a23a=33－12.

故BEEF的最大值为23-36.

思考2将正方形ABCD换成矩形ABCD，Rt△ABC（∠B=90°），其余条件不变，对问题结果有影响吗？经探究，是没有影响的.

2.2改变图形形状

例2如图5，在菱形ABCD中，∠B=120°，点E，F在射线BC上，∠EAF=30°，求BEEF的最大值.

解利用一线三等角.

如图5，作∠AEG=∠B=120°交AF于点G，则∠AGE=∠GAE=30°，所以GE=AE.

因为∠AEB+∠GEF=180°－120°=60°，

又∠AEB+∠BAE=180°－120°=60°，

所以∠GEF=∠BAE，

作∠EGM=∠AEB交EF于点M，

所以△EMG≌△ABE（AAS），

所以MG=BE.

作△EFG的外接圆，设圆心为O，连接OE，OF，OG，则OE=OF=OG.

因为∠EGF=∠EAF+∠AEG=150°，所以∠EOF=60°，

所以△EFO为等边三角形.

分别过点G，O作GP⊥EF于点P，OQ⊥EF于点Q，连接OG，则GP+OQ≤OG，所以GP≤OG－OQ，当点P，Q重合在OG上时取等号.

设EQ=FQ=a，则OG=OE=EF=2a，于是OQ=3a，

所以GP≤2a－3a.

由于∠GMP=180°－∠EMG=60°，所以∠GMP=∠OFQ=60°.

易证Rt△MPG∽Rt△FQO，所以MGOF=GPOQ，

所以BEEF=MGOF=GPOQ≤2a－3a3a=233－1.

故BEEF的最大值为23-3[]3.

2.3改变图形形状和数据

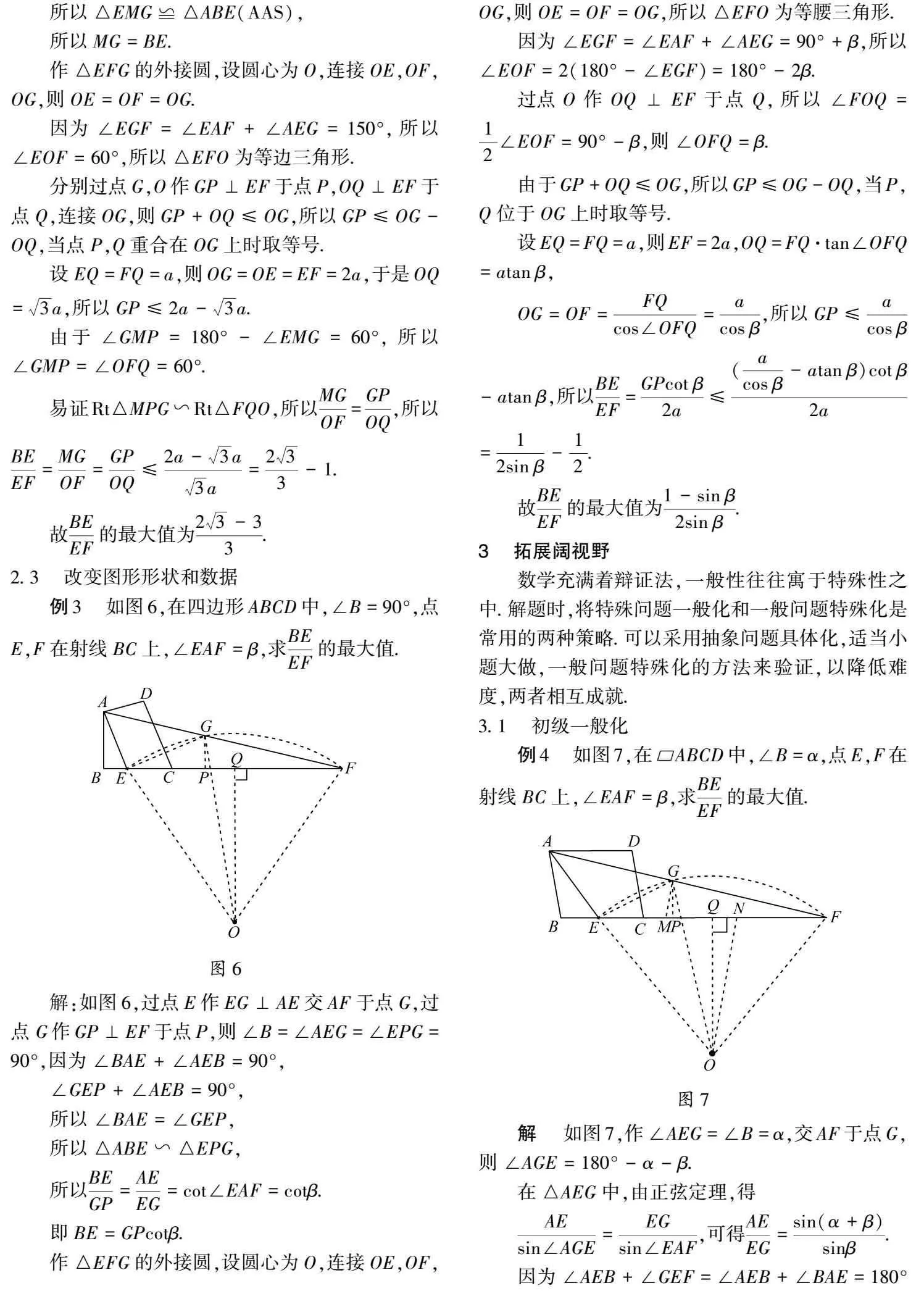
例3如图6，在四边形ABCD中，∠B=90°，点E，F在射线BC上，∠EAF=β，求BEEF的最大值.

解：如图6，过点E作EG⊥AE交AF于点G，过点G作GP⊥EF于点P，则∠B=∠AEG=∠EPG=90°，

因为∠BAE+∠AEB=90°，

∠GEP+∠AEB=90°，

所以∠BAE=∠GEP，

所以△ABE∽△EPG，

所以BEGP=AEEG=cot∠EAF=cotβ.

即BE=GPcotβ.

作△EFG的外接圆，设圆心为O，连接OE，OF，OG，则OE=OF=OG，所以△EFO为等腰三角形.

因为∠EGF=∠EAF+∠AEG=90°+β，

所以∠EOF=2（180°－∠EGF）=180°－2β.

过点O作OQ⊥EF于点Q，

所以∠FOQ=12∠EOF=90°－β，则∠OFQ=β.

由于GP+OQ≤OG，

所以GP≤OG－OQ，当P，Q位于OG上时取等号.

设EQ=FQ=a，则EF=2a，OQ=FQ·tan∠OFQ=atanβ，

OG=OF=FQcos∠OFQ=acosβ，所以GP≤acosβ－atanβ，

所以BEEF=GPcotβ2a≤（acosβ－atanβ）cotβ2a=12sinβ－12.

故BEEF的最大值为1-sinβ2sinβ.

3拓展阔视野

数学充满着辩证法，一般性往往寓于特殊性之中.解题时，将特殊问题一般化和一般问题特殊化是常用的两种策略.可以采用抽象问题具体化，适当小题大做，一般问题特殊化的方法来验证，以降低难度，两者相互成就.

3.1初级一般化

例4如图7，在ABCD中，∠B=α，点E，F在射线BC上，∠EAF=β，求BEEF的最大值.

解如图7，作∠AEG=∠B=α，交AF于点G，则∠AGE=180°－α－β.

在△AEG中，由正弦定理，得

AEsin∠AGE=EGsin∠EAF，

可得AEEG=sin（α+β）sinβ.

因为∠AEB+∠GEF=∠AEB+∠BAE=180°－α，

所以∠GEF=∠BAE.

作∠EGM=∠AEB交EF于点M，则△EMG∽△AEB，所以AEEG=BEMG.

所以BEMG=sin（α+β）sinβ.①

作△EFG的外接圆，设圆心为O，连接OE，OF，OG，则OE=OF=OG，所以△EFO为等腰三角形.

因为∠EGF=∠AEG+∠EAF=α+β，

所以∠EOF=2（180°－∠EGF）=2（180°－α-β）.

过点O作OQ⊥EF于点Q，过点G作GP⊥EF于点P，则GP+OQ≤OG，

所以GP≤OG－OQ，当P，Q位于OG上时取等号.

所以∠FOQ=12∠EOF=180°－α-β.

设EQ=FQ=a，则EF=2a，在Rt△OFQ中，OQ=FQ[]tan∠FOQ=-a[]tan（α+β），

OG=OF=FQsin∠FOQ=asin（α+β），所以GP≤asin（α+β）+a[]tan（α+β），

因为∠GMP=180°－∠EMG=180°－α，

过点O作ON∥MG交EF于点N，可得∠ONQ=∠GMP=180°－α，

易证Rt△GMP∽Rt△ONQ，所以GPMG=OQON，

所以GPMG=OQON=sin∠ONQ，即GPMG=sin（180°－α）=sinα.②

①÷②式，得BE=sin（α+β）sinαsinβGP.

所以BE≤sin（α+β）sinαsinβasin（α+β）+a[]tan（α+β），

所以BEEF≤sin（α+β）sinαsinβasin（α+β）+a[]tan（α+β）÷2a=1+cos（α+β）2sinαsinβ.

故BEEF的最大值为1+cos（α+β）2sinαsinβ.

3.2高级一般化

问题如图8，在四边形ABCD中，∠B=α，点E，F在射线BC上，∠EAF=β，求BEEF的最大值.

借助第3.1节的探究，获得同第3.1节一样的结果，说明问题结果与图形形状无关，只与有关角度大小有关.综合可见，构造等角和利用隐圆是解题关键，文前试题、例1均为例3问题的特殊情况，包括例2均为例4的特例.例4虽已超出初中范畴，但作为教师却有探析的必要.

思考3将四边形ABCD换成△ABC，其余条件不变，结果还成立吗？经探究，结果仍成立.

多角度、逐级深入地进行观察和思考，是收获“以少胜多”的成功秘密.让孩子在未来有能力去应对当今世界各种错综复杂的现实问题，在始末之间，是对知识与问题不断拆分与整合中的探究、分析、构建、融通和创造的能力.这就是我们数学教学追求的能力目标.在一题多用的过程中，把握难度，选择时机和对象，合理用之，避免过度和滥用.

参考文献

[1]毕里兵.注重“一题多解、一题多变”追求有效教学：记一堂高三复习公开课及教学反思[J].中学教研（数学），2011（11）：23-25.

陈蓉Angel，以“现象式教学”揭开芬兰以少胜多的秘密，https：//www.sohu.com/a/338761087_303054，2019.9.4

作者简介

李发勇（1964—），男，四川巴中人，中学高级教师;主要从事初中数学教学研究，在多种数学专业期刊发表教研文章100余篇.