大概念视角下的初中数学教材比较研究

【摘要】“大概念”在培养与实现学科核心素养方面有其独特的作用与价值.在阐述数学大概念的基础上，对其划分为课时大概念、单元大概念、单元间大概念和学科大概念四个有逻辑关系的大概念层.建立比较框架，从知识的内涵、知识的编排、知识间的关系和知识的学科价值四个维度对中国和新加坡数学教材中“一次函数”的内容进行比较研究.基于研究结果，对教材编写者修订教材和教师、学生使用教材提供参考.

【关键词】大概念；初中数学；教材比较；人教版教材；新加坡教材

新加坡于2020年9月实施了最新的中学数学课程大纲[1]，其中包括了八个数学学科大概念（Big Ideas）.至此，新加坡成为数不多的几个将数学大概念纳入课程标准的国家之一，可见新加坡在运用数学学科大概念优化数学教育改革相较我国已有一定的经验.本研究将对中国和新加坡初中数学教材中一次函数的内容进行比较，以期使得教材中的大概念更合理、更有效地提取出来，实现对教材资源的优化利用.

1数学大概念内涵及层级划分数学教育也许是第一个把大概念带进课堂的科目.

目前，具有典型意义的数学大概念内涵，是查尔斯在2005年提出的“大概念是对数学学习的核心概念的表述，能够将人们对数学不同的理解和认识形成一个统一的整体”[2].我国学者则认为数学大概念是一种对数学知识进行再建构的过程，用“少而精”的大概念，让学生对数学有更深刻的认识，这对于贯彻核心素养来说是至关重要的[3-5].

但是，数学大概念具有抽象性和概括性，要想获得需得有很好的学习和总结.因此，在教学过程中，需要以单元教学为基础.但是，它也是一个相对的概念，因而有层次的区别.义务教育课程标准将数学学科划分为不同的领域，每个领域下又划分为不同的单元，单元间的相互作用构成了各领域的大概念；而单元大概念则是由一个个课时的内容联结而成.如图1所示，学科大概念位于层级结构的顶层，可以反映学科的本质；单元间大概念是学科大概念在各个单元中的体现，以此串联成这个领域中的核心概念；单元大概念是单元间大概念在各个单元中的体现，使得知识结构化；课时大概念则是构成单元大概念的基础，大概念的学习需要依托课时教学内容.

2研究设计

2.1研究对象选取

我国教材选取的是人民教育出版社的《义务教育教科书·数学》（以下称人教版教材），新加坡教材选取的是Marshall Cavendish Education出版的《New Mathematics Counts》（Academic）（以下称新加坡教材）.选取两国教材中与“一次函数”相关的章节进行比较分析，并提取其中有关一次函数的大概念.

2.2研究比较的框架构建

目前对于数学大概念的提取方式研究众多.但无论是从知识逻辑提取[6]还是按学生经验提取[7]都无法为教材比较的视角提供有效的参考.所以需要以数学大概念的层级作为依据创建相应的教材比较框架.

李松林[8]提出通过对教材的深度理解，可以让大概念萌芽，并提出了深度理解教材的五个方面，即可以分别从知识的产生与来源、事物的本质与规律、学科思想与方法、知识的关系与结构和知识的作用与价值来深度理解教材.本研究从五个方面作为提取维度，结合数学大概念的层级结构，分别从知识的内涵、知识的编排、知识间的关系和知识的学科价值四个方面对教材进行比较.两国初中数学教材中大概念的提炼以及教材比较框架如表1所示.

3两国初中数学教材中“一次函数”内容比较分析

3.1课时大概念——知识内涵

课时大概念的提取目的是让学生对每一节课的具体内容和问题有一个较好的把握.其在单元教学中起到承上启下的作用，既要能够促进单元大概念的理解和掌握，又要便于教师的数学教学和学生的理解，因此课时大概念的表述需要尽可能地符合学生的理解水平[9].所以在提取课时大概念时需要仔细研读教材和课程标准，对两国教材中“一次函数”的知识内容进行比较，聚焦知识的内涵，通过对教材每小节的内容梳理，从知识内涵的角度分析和概括出课时大概念，结果见表2.

说明：由于新加坡教材中有三本教材涉及一次函数内容，因此在整理课时内容时添加教材编号加以说明.如第2册教材第3单元第4节中的第1小节则记为：二—3.4.1，以此类推.

从表2可知，两国教材在“一次函数”部分的知识容量类似.包含的知识有：一般函数的概念和定义；一次函数的定义和图象性质；确定一次函数的解析式以及一次函数与方程的关系.不同之处在于，人教版还有一次函数与不等式的关系，以及两国在一次函数的实际运用中侧重内容不同.人教版以选择方案为实际问题情境，旨在让学生尝试用一次函数模型解决问题；新加坡教材则是侧重一次函数图象与物理知识结合，用一次函数模型刻画行程问题.

3.2单元大概念——知识的编排

单元大概念让老师对单元—课时教学有了更高的认识，它不仅是学生单元学习的终极目的，同时也是老师对整体教学进行反思的逻辑出发点.分析两国教材中的课时大概念以及“一次函数”内容所在章节，基于知识的关系和结构，从知识编排的角度对两国教材的单元大概念进行提炼，结果如表3.

通过梳理单元大概念，可以发现，两国教材研究函数的一般顺序均为刻画一次函数定义，研究图象性质，最终运用一次函数模型解决问题.虽然我国在高中阶段也会从解析几何即代数角度入手探讨函数的性质，但相比之下，新加坡在初中阶段就已经介绍用代数方法研究函数图象，并且将一次函数放置在平面直角坐标系之后，直观感受几何直观和代数运算的融合.

3.3单元间大概念——知识间的关系

函数作为一种刻画变化关系的工具，不应局限在某一章节中去探讨和研究.两国教材均注意到了这一方面，因而都将函数与其他单元的知识建立起联系.通过对单元间大概念的提炼，可以统摄同一类数学知识的核心概念或数学学科思想、方法与观念.因此，本研究从知识间的关系对两国教材进行较为宏观的比较，从学科的思想和方法角度进行单元间大概念的提炼.两版教材单元间大概念提取，如表4.

从单元间大概念提取的情况看，两国教材均重视知识之间的内在联系，引导学生体会函数观点的统率作用.有所不同的是，在用函数观点看方程、不等式方面，新加坡版教材将方程组单元构建联系，但却深挖方程组解的多种可能，使得学生能借助图象寻求一次方程组的根.而人教版则是用一次函数把以前学习的方程和不等式进行整合.从函数的取值和图象两方面将一次方程（组）和不等式这些老概念纳入新的知识体系中.

从知识运用的角度来看，人教版注重考查运用一次函数解决实际问题，并着重培养学生函数建模的思想.其单元间的大概念主要与方程、不等式建立联系，在没有接触函数之前，学生解决策略最优问题时使用最多的是不等式思想，当满足条件的情况较多时不便于快速找到问题的最优解.在引入一次函数概念时，学生可以运用其性质快速解决问题.相比人教版，新加坡版教材在编排时则更注重数学与物理的跨学科主题研究.以物理学中刻画物体的运动状态为引子，运用一次函数图象研究物体运动时的四个基本量：速度、时间、路程和加速度.从一次函数的视角解读四个基本量的意义，运用图象性质计算具体数值.

从单元间大概念提取的情况看，两国教材均重视知识之间的内在联系，引导学生体会函数观点的统率作用.有所不同的是，在用函数观点看方程、不等式方面，新加坡教材仅将函数和解一次方程组结合，运用一次函数图象刻画方程组解的不同情况.虽然仅与方程组单元构建联系，同时深挖方程组解的多种可能，使得学生能借助图象寻求一次方程组的根.而人教版教材则是运用一次函数将以前学习的方程和不等式进行整合.从函数的取值和图象两方面将一次方程（组）和不等式这些老概念纳入新的知识体系中.

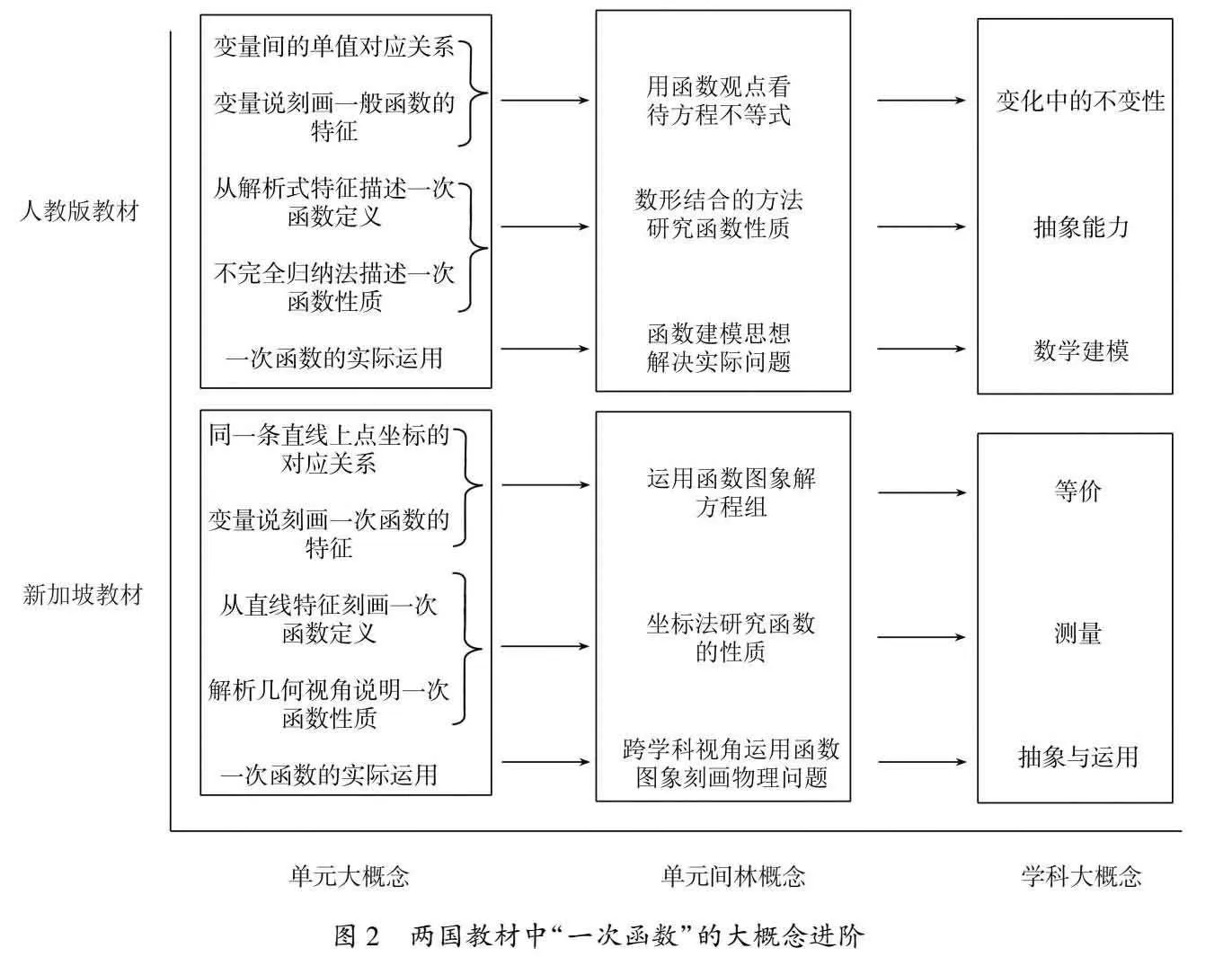
3.4学科大概念——知识的学科价值

数学学科大概念能够体现出数学学科的性质，处于科目的核心位置.通过对单元大概念和单元间大概念的抽象概括，可以得到学科大概念.因此将两国教材中的单元大概念、单元间大概念进行抽象概括得到了“一次函数”内容中涉及的学科大概念，如图2所示.从事物的本质与规律来看，人教版旨在帮助学生认识到事物变化中的不变性.例如，寻找一个二元一次方程的解，在没有限定解集的情况下，其中一个未知量的解会随着另一个未知量而改变，但两个变量之间的关系是确定的，从一次函数的角度看，两个变量不管如何变化，其始终在一条直线上.新加坡版教材则是构建出“等价”这个学科大概念来刻画事物的本质和事物间的规律.等价是表示“相等”的两个事物之间的一种联系，可以用多种不同的方式来表示.从一种形式的等价到另外一种形式，是进行分析c10a4259a2f0d9d4ede9080f96b3fc54、比较和解答等多种运算的前提.图2两国教材中“一次函数”的大概念进阶

从知识的学科价值角度来看，两国教材都注重培养学生抽象能力.有所不同的是，人教版教材注重从实际情境中抽象出核心变量，经过数学建模后，用一次函数的图象和性质描述变量之间的相互关系.新加坡教材则看重从跨学科的问题中抽象出变量之间的关系，尤其以数学和物理的跨学科问题居多，用一次函数的图象刻画物理问题从而得到一般结论和规律.另外，从新加坡教材中，笔者还提取到另一个学科大概念——“测量”.其采取的是“坐标法”研究一次函数的性质，与平面直角坐标系中的计算问题、线段长度的度量和斜率的计算合在一个大单元中，旨在帮助学生从“数”的角度量化一次函数的研究，感受几何与代数运算的深度融合.因此，“测量”这个学科大概念贯彻在数学学习的各个领域，发挥着量化研究的重要作用.

4启示

研究教材对比的目的在于了解不同教材的长处与短处，以便借鉴“他山之石”[10].但是，教材编排只是其中一个方面，其功能的发挥还受制于教师怎样组织教材、采取什么样的教学方法.因此，对教材内容进行对比分析，或许能为教材编写者修订教材、教师和学生使用教材提供一些新的视角.

首先，从教材编写的角度看，人教版教材在一次函数的学习中提供了大量的现实素材，引导学生从具体到抽象地认识函数.面向真实情境的大概念教学强调让学生看见学科知识与现实世界的关联，注重学习过程中相关知识之间的联系，以求得真实性的问题解决[11].以真实情境为载体，研究函数的概念和性质，这是我国教材编写的特点与优势.然而，与新加坡数学教材对比后发现，其还结合了物理学科的知识背景，专门用一小节的内容篇幅介绍一次函数图形和性质在物理学中的运用，体现了其跨学科融合的思想，这是人教版教材值得借鉴的地方.因为，大概念不只是局限于特定的学科领域，而具有通用性[12]7.此外，可以发现新加坡教材在编排一次函数内容时，将其分散在不同书目中.第二册教材介绍一次函数的概念并渗透函数思想；第三册教材详细介绍一次函数的变化率及其解析式的求法；第四册教材介绍其在实际问题中的运用.用“等价”“测量”等学科大概念串联一次函数知识，采用螺旋式编排，这样使各个数学科目在总体内容上达到了协调和统一，体现了课程内容中各部分之间本身固有的连贯性以及各册教材之间的联系，同时，也符合学生心理特征[13].因此，如何用学科大概念将函数知识进行合理整合，是我国教材编写者需要考虑的问题.

其次，从教师的角度来看，可以大概念为支点，设计教学目标及活动.教师在使用教材时，可以借助概念图提取各级大概念，明晰单元知识结构，研究函数单元教学设计路径，亦可引导教师以大概念为锚点连接课程与课时[14].第一步，基于课标要求与素养指向，通过构建概念图提炼函数大概念，确定单元学习目标；第二步，根据函数概念特征及学情分析，分析课时大概念并进行每一小节的教学设计；第三步，解析概念层级之间的关系，调整教学设计，确保函数大概念在单元教学中的一致性.以大概念为支点，通过函数单元整体设计，是实现课程、教学与评价的一致性，是初中数学课堂落实核心素养培育的重要途径[15].

最后，从学生的角度来看，大概念可以为其学习提供学习线索[12]9.掌握了变化中的不变性、数学建模思想等学科大概念时，他们可以从运动变化的视角分析问题，理解一次函数的概念；梳理了单元间的大概念和单元大概念后，可以以这些大概念为线索，自己构建出一次函数的单元知识结构图.这能够帮助其在不借助教材或其他教辅书时，完整地提取出单元的核心知识，并解决问题.进一步地，学生通过自我阅读或教师指导，提取大概念后，能够解决学生思维发展低阶性、课时之间零散性和单元之间割裂性等现实问题，进而促进其对学科大概念的深度理解与学科核心素养的培育[16].

参考文献

[1]陈碧芬，金蓓霜.中国、新加坡初中数学课程标准中的核心素养比较研究[J].天津市教科院学报，2022，34（04）：67-72.

[2]廖运章，张铭慧.大概念取向的新加坡2020中学数学大纲述论[J].教育导刊，2022（04）：85-96.

[3]王惠.基于学科“大概念”的初中数学教学[J].教学与管理，2021（22）：64-66.

[4]黄兴民.“大概念”统摄下的数学教学[J].数学教学通讯，2021（16）：55-56.

[5]吕增锋.高中数学大概念的内涵及提取[J].中小学教师培训，2021（07）：53-55.

[6]夏繁军.“数学大概念”的提取与论证[J].基础教育课程，2022（Z1）：87-94.

[7]吕增锋.高中数学大概念的内涵及提取[J].中小学教师培训，2021（07）：53-55.

[8]李松林.以大概念为核心的整合性教学[J].课程·教材·教法，2020，40（10）：56-61.

[9]卜梦丹，唐恒钧.数学大概念的内涵、提取途径及其理解维度[J].中小学教师培训，2022（07）：36-39.

[10]王科，汪晓勤.“中美日新”四国高中教材中的数学归纳法比较研究[J].数学教育学报，2015，24（02）：40-45.

[11]李凯，吴刚平.为素养而教：大概念教学理论指向与教学意蕴[J].比较教育研究，2022，44（04）：62-71.

[12]李凯，范敏.素养时代大概念的生成与表达：理论诠释与行动路径[J].全球教育展望，2022，51（03）：3-19.

[13]王林全.国内外高中数学教材发展的若干趋势[J].学科教育，2003（09）：45-49.

[14]钟启泉.单元设计：撬动课堂转型的一个支点[J].教育发展研究，2015（24）：1-5.

[15]斯海霞，叶立军.大概念视角下的初中数学单元整体教学设计：以函数为例[J].数学通报，2021，60（07）：23-28.

[16]占小红，刘欣欣，杨笑.基于学科大概念的单元教学设计模式与类型化研究[J].上海教育科研，2022（09）：75-81.

作者简介

沈爱桐（1997—）女，云南昆明人，硕士研究生;研究方向为数学教育.

杨亚平（1987—）女，云南大理人，博士，副教授，硕士生导师;研究方向为STEM教育和数学教育.