基于STEAM理念的数学文化项目学习设计

【摘要】数学文化项目学习指向知识的深度理解与关联，符合学生数学核心素养培育的诉求.立足STEAM理念，结合“找寻中式古建冠冕中的数学”，从项目启动阶段、项目规划阶段、项目开展阶段、项目公开评价4个关键教学阶段出发，探讨了基于STEAM理念的数学文化项目学习设计.

【关键词】STEAM；数学文化；项目学习；古代建筑;中式屋顶

STEAM教育是一种综合性的教育模式，它将科学、技术、工程、艺术和数学融合在一起，旨在培养学生的创新能力、解决问题的能力和团队合作精神.STEAM教育的核心理念是将不同学科之间的知识和技能相互融合，以创造性的方式解决实际问题.STEAM教育可以概括为“以数学为基础，通过工程和艺术解读科学和技术”[1].数学被视为STEAM教育的基石，能够促成科学、技术、工程和艺术四门学科的有机融合.数学文化作为数学教育内容的重要组成部分，其实质是以数学学科为核心，统整融合自然、人文、社会等学科[2].值得注意的是，数学文化、STEAM理念和项目式学习在强调学科融合、解决真实问题、促进创新能力培养等方面存在耦合性[3].鉴于此，开发基于STEAM理念的数学文化项目学习案例是值得关注和探赜的.本文尝试以“找寻中式古建冠冕中的数学”为例，以期力证STEAM理念、数学文化和项目式学习的优势联动关系，为高中数学教学开展跨学科活动提供可行的思路与路径；同时挖掘中国古代建筑蕴藏的数学教育价值，丰富中国本土化的教学资源库以此探索具有中国特色的项目学习.

1项目启动阶段

1.1主题统整

主题统整指向的是STEAM理念下数学文化项目学习的认知结构层面，是项目学习发生的基本抓手，是整个数学文化教学的核心.而如何将文化主题以项目式学习活动的形式进行设计，并拆解成以数学学科为中心、融合各学科的学习内容，是案例开发的关键.鉴于此，STEAM理念下的数学文化项目学习的主题统整可以从文化、数学和学科三大角度斟酌.

从文化关联角度来看，屋顶是中国古代建筑的冠冕，是我国传统建筑的主要构造与形态表征，是民族审美文化的张扬.就中式屋顶的物质层面而论，屋顶的形态成因、多样类型、精妙营造有待探究.就中式屋顶的精神层面而言，蕴含着天人合一、道法自然的理念和原生质朴、简约和谐的中式美学，凝聚着中华优秀传统文化的气韵神形.因此，中式屋顶作为中国本土化的教学资源亟待挖掘，可以进一步设计中国特色的项目学习.

从数学关联角度来看，以屋顶为主题的项目学习包含圆锥曲线和三角函数两个主要知识.以椭圆、双曲线以及抛物线等曲线为学习生长点，探究最速降线的存在性；利用三角函数、导数演绎推理求解抛物线和摆线方程.其中蕴含函数与方程、数形结合、建立数学模型等数学思想方法.通过数学文化的融入，使学生感悟约翰·伯努利、莱布尼茨等数学家们刻苦钻研、探索真理的精神；在屋顶模型的制作与鉴赏中感受数学的对称美与和谐美.因此，基于屋顶蕴含的数学元素，可以开展数学文化学习.

从学科关联角度来看，屋顶中蕴藏着多学科属性，探究屋面中最速降线是否存在属于科学实验的过程，而最速降线方程的推导借助物理学科中的光的折射、能量守恒定律和平抛运动等内容.同时，加入信息技术软件制作曲线、拟合曲线、工程设计并艺术欣赏屋顶模型.概言之，与物理、工程、技术和艺术等学科的知识密切相关，可以开展以中式古建屋顶为主题的数学文化项目学习.

结合以上文化、数学和学科三大视角，本文尝试将项目主题统整为“找寻中式古建冠冕中的数学”，围绕中式古建筑的屋顶模型这一构建性作品的制作及其蕴含的多学科知识等展开学习.

1.2目标确定

基于STEAM理念的数学文化项目式学习不仅要凸显数学的文化价值和跨学科价值[4]，同时，项目化学习的中国建构需要价值观作为灵魂[5].因此，具体细分为基础知识、能力素养和精神品质三个维度.

基础知识：能够借助物理中光的折射、能量守恒定律等内容以及数学中三角函数和导数等内容演绎推理获得最速降线存在的条件以及相应的曲线方程；能够结合平抛运动探索其中蕴含的抛物线方程；了解费马光速最值原理、斯涅尔定律等科学定理以及几何画图软件的基本操作.

能力素养：协商简易中式古建筑的屋顶模型的实施方案，培养全局意识和工程思维；能够借助数学中圆、双曲线和抛物线等曲线进行实验，培养实验探究的能力；推理得到最速降线方程，整理数据并提取信息，构建曲线模型，发展逻辑推理、数学建模和数据分析等数学学科核心素养；利用GeoGebra技术软件绘制圆锥曲线和最速降线、拟合抛物线，实现数字化学习与创新，发展批判性思维；在欣赏并制作屋顶模型中，增强创新设计和物化等能力.

精神品质：渗透最速降线的数学文化，卷入曲折的探索历程，在领悟数学家们坚持不懈、追求真理的精神的同时，生成动态的、易谬主义的数学观，感受数学臻于完善的过程；在认识曲线与其他学科的关联中，感悟数学的跨学科内涵与科学价值、应用价值、文化价值和审美价值等价值观念，塑造乐学善学、探究创新和团结合作的态度与品质；在屋顶模型的物化中，洞见中国古代劳动人民的智慧，理解文化保护的社会责任，实现文化持续性教学.

2项目规划阶段

师生活动：在确定项目主题与目标后，挖掘最速降线的相关史料、数学家故事等数学文化作为项目素材.聚焦项目成果，师生统筹规划后，降维拆解如下三大关联任务.

任务1：探究屋顶的“吐水疾”：借助小球轨道的科学实验，探究能够使雨水下落速度最快的屋顶的最优曲线，并用技术工具拟合曲线.

任务2：探究屋顶“溜水远”：在保证排水速度最快的基础上，进一步探究能够使屋顶雨水排至最远的曲线.

任务3：举屋营造制作屋顶模型：补充举架、举折和提栈等相关建筑知识，制作简易的中式屋顶模型并规划与举办展览活动.同时，进一步优化改进模型并延伸思考，制作更多不同类型的传统屋顶.

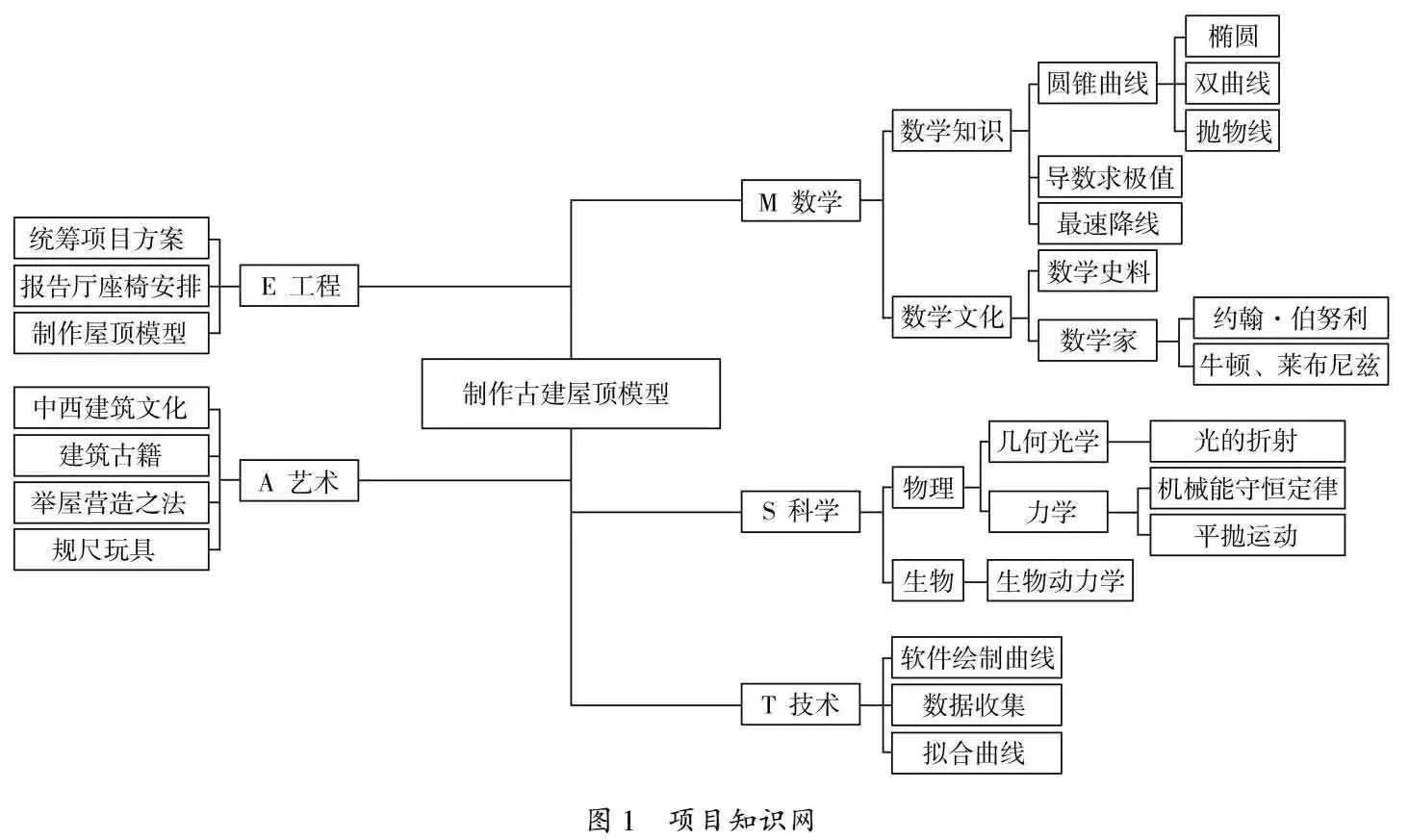
同时，师生立足STEAM理念，共建项目知识网（图1），为学生的持续性探究提供索引，回归最终成品的产出.本项目规划为2个课时，其中第一课时完成任务1，第二课时展开任务2，3.

3项目开展阶段

环节1：创设情境，识别问题

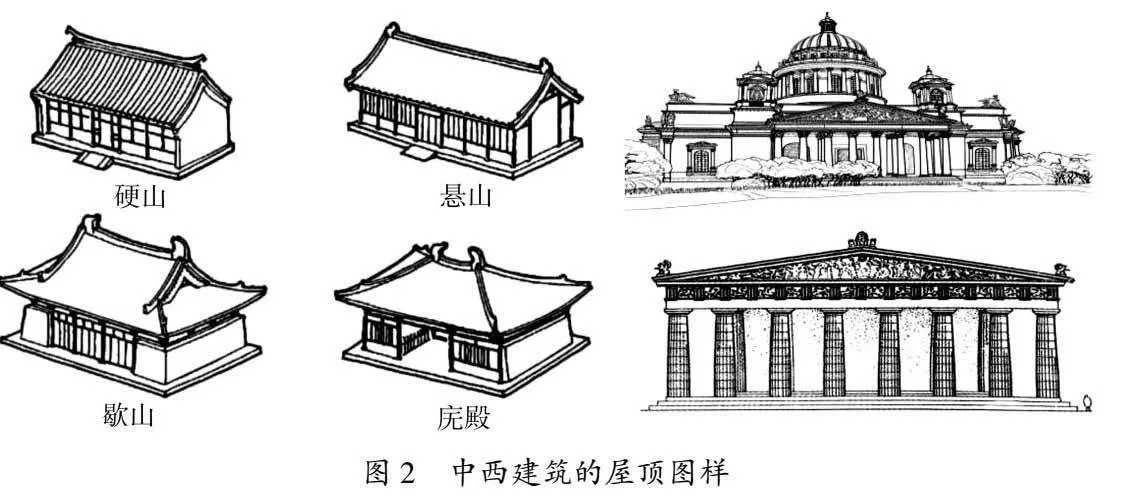
我国传统建筑从外形上分为下中上三部分，大体为三段式结构，即由屋顶、屋身和台基三个基本部分构成.屋顶是房屋建筑的冠冕，承载着中华五千年的历史.无论是庑殿、歇山、硬山还是悬山屋顶式的建筑，在屋顶曲线中都呈现出一种越向上越陡峭，越向下越平缓的反曲屋面形式.这种反曲屋面是中国古代建筑的重要特征之一，是功能、结构、形式的高度统一.今天，就让我们一起走进中式建筑的冠冕，找寻屋顶中的数学密码.

问题1-1：如图2，观察中西方单体类建筑的屋顶图样，它们的屋顶面有什么不同？而中式建筑的屋顶具有什么样的特征？

问题1-2：为什么中国古建筑的屋顶大都采用曲形屋面？

问题1-3：屋顶模型的制作过程蕴含了大量的数学知识.建筑和数学究竟有着什么关系？我们是否可以借助数学知识，动手制作一个简易的中式古建筑的屋顶模型呢？

师生活动：学生小组间展开交流，比较中西建筑屋顶的形状特征及功能需求，逐渐将话题聚焦于中式建筑特有的凹面屋顶，鼓励不同文化背景、不同发展水平的学生提出屋顶生成机制的合理猜想，加深学生对中式建筑的文化感知与鉴赏.为丰富学生的认知，教师补充生成凹面屋顶的已有推论，包括帐幕说、杉树说、构造说和功能说等，为后续的项目探究埋下伏笔.

设计意图：创设文化情境，调动学生积极的情绪准备，体会中西建筑文化的异同，进而加深学生对中式建筑的文化感知与文化鉴赏.从兼具开放性和弹性的真实问题出发，为不同文化背景、发展水平的学生留有适切的思考起点和充盈的思考空间，以此生成的答案富有原创性和复杂性，培养学生收集信息的能力和批判性思维.同时，制作屋顶模型这一项目成果为学生能够以数学的眼光、数学的思维以及数学的语言观察、思考和表达现实问题提供机会，构建贯穿学生学习始终的数学生态场域，进一步找寻中式古建冠冕屋顶中的数学.

任务1：探究屋顶的“吐水疾”.

环节2：组建团队，科学实验

师生活动：学生讨论坡曲屋顶的成因分析后，教师引导学生集中于功能说，进一步探究屋顶排水这一功能的合理性和科学性.考虑到接下来的任务形式多样且具有一定的挑战性，学生通过填写索引卡选择合作伙伴以此组建有效合作团队.

问题2-1：当雨水分别从斜面屋顶和曲面屋顶向下滑，哪种屋面下滑速度快？你能尝试用实验验证你的猜想吗？

师生活动：基于对“两点之间线段最短”这一定理的熟知，学生容易产生思维定势，即错误推测斜面屋顶上的雨水下落最快.为了纠正这一误解，开展科学实验显得尤为必要，而真实的屋顶实验存在安全隐患，师生进行乒乓球轨道的模拟实验，利用硬纸板、热熔胶和铁丝等材料分别制作两条等高等底的直线和曲线轨道.实验中，学生把乒乓球放置在轨道顶端后，同一时间松开小球令其自行下滑.考虑到乒乓球的弹性和重量等因素产生误差，调换乒乓球所在的轨道，重复以上实验并取平均值.

问题2-2：在科学实验中我们发现在曲面轨道上的小球下滑速度更快，相当于曲面屋顶的排水功能更好，结合之前所学的数学知识，你能否试着猜想一下这是一条怎么样的曲线？

师生活动：学生联系过去所学习的不同曲线，猜测这条曲线可能是圆弧、椭圆、双曲线或抛物线.为了验证猜想，小组合作制作以上的曲线轨道与教师课前准备好能使小球最快下落的轨道进行对比实验.

数学文化融入：追溯至1630年，意大利科学家伽利略也陷入了同样的困惑：当一个质点在重力作用下，从一给定的点滑向其下方不垂直的另一点时，若不考虑摩擦力，质点沿着怎样的曲线滑下所需时间最短.伽利略的猜想是圆弧，但从以上实验中我们可以发现圆弧并非正确答案.直到1696年，瑞士数学家约翰·伯努利就这一问题向全欧洲的数学家发起公开挑战.约翰·伯努利在求解这一问题时运用到了几何光学的知识，接下来我们一起来看看他是如何探究的？

设计意图：鉴于学生的文化认知兼具同喻性和不均衡性，教师应思虑创建什么样类型的团队，以及什么时候需要进行团队合作，才能使生生共创形成学习共同体，在互动中培养合作技能以及引发深度学习.学生熟知“两点之间线段最短”这一定理，自然会产生思维定势，由路程最短猜测斜面屋顶上的雨水下落时间最短，这正符合最初古希腊数学家的论断.开展小球轨道的科学实验，既可以积累数学基本活动经验，又直接得到路程最短的线路并不等同于所用时间最短的路线的实验结果，引起学生的认知冲突，激发探究兴趣.数学文化的融入，使学生能够跟随数学家的脚步经历数学的发展过程，从中让学生感受到数学知识的生长性和建构性，进而产生文化共鸣.

环节3：类比推理，数学求解

科学融入：学生在课前回顾物理选择性必修中的几何光学知识，包括折射、折射率、折射率与速度之间的关系和光程等基本概念.教师补充介绍费马光速最值原理，引导学生将小球下滑的过程等效成光在折射率连续变化的介质中传播的过程，类比折射光线在不同介质中光程取极值路径的性质，小球在轨道的下落运动过程中也可以分成若干个不同区域.

问题2-3：如图3所示，设A，B两点分别位于折射率为n1，n2的介质中，A，B两点的横向距离为d，纵向距离为2l.两种介质的分界面位于x轴，光在C点发生折射，位置为（x，0）.其中入射光线AC为l1，出射光线CB为l2，入射角为θ1，折射角为θ2.能否利用数学知识，推导从A点到B点的光程取极值时应满足什么条件吗？

师生活动：由于数学所研究的是纯粹的量，因此，不能满足于对数学命题进行实际的检验，还必须从理论上加以论证[6].学生首先计算得到光线从A点到B点走过的路程为s=n1l1+n2l2=n1l2+x2+n2l2+（d-x）2，因为s是x的函数，对其求导后可得dsdx=n12x2l2+x2+n22（x-d）2l2+（d-x）2=n1xl1+n2x-dl2=n1sinθ1-n2sinθ2，当导数等于0时，满足n1sinθ1=n2sinθ2.学生发现光线从一种介质进入另一种介质时，传播方向通常会发生改变，其入射角、折射角与两种介质的折射率之间存在关系.教师进行补充说明该结论最初由荷兰数学家威里布里德·斯涅耳发现，称为斯涅尔定律（光的折射定律）.

学生进行公式代换，将v1=cn1，v2=cn2代入n1sinθ1=n2sinθ2，其中v1，v2分别是光线在两种介质中传播的速度，c为真空中的光速，可得sinθ1v1=sinθ2v2，可以发现光在介质中的传播速度与界面法线的夹角的比值为常数，记为sinθv=C.

问题2-4：如图4所示，设屋顶面的雨水从A到B运动过程中任一位置纵坐标y对应的速度为v，v与y轴方向的夹角α，与x轴方向的夹角为φ，是否存在这样一条使雨水下滑时间最短的屋顶曲线呢？类比光线传播，你能试试推导这条曲线的方程吗？

师生活动：类比光线沿着光程为极值的路径传播应满足的条件sinθv=C，雨水下滑运动同样适用.根据机械能守恒定律，雨水的运动速度记为v=2gy.因为雨水运动位置与x轴方向的夹角为φ，所以y′=tanφ，而sinα=cosφ=11+tan2φ=11+y′2.那么sinαv=12gy1+y′2=C，可以求出这条使雨水下滑时间最短的曲线的微分方程y（1+y′2）=C.

学生将y（1+y′2）=C转化为dx=yC-ydy后，发现方程形式依旧复杂.故教师引导学生利用三角函数的知识将方程中的根号去掉，令y=Csin2φ，则dx=C（1-cos2φ）dφ，x=C2（2φ-sin2φ）+C0（C0为任意常数）.出于对方程简洁性的考虑，由A点为坐标原点确定C0=0，令θ=2φ，R=C2，最终得出曲线方程为x=R（θ-sinθ），y=R（1-cosθ）.

数学文化融入：数学家约翰·伯努利将这条曲线称为“最速降线”，又名摆线.最速降线问题可以说是数学史上最鼓舞人心的一次公开挑战.首先，参与挑战的人数空前，且得出正确答案的数学家颇负盛名.例如，牛顿和莱布尼茨从不同角度入手建立了微积分；而伯努利兄弟二人是奇迹家族中的杰出人物；洛必达年幼时就展露出数学天赋并解决了摆线难题.其次，挑战中出现的解法各有千秋，其中雅各布·伯努利的解法表露出了变分的思想且更具普适性和广泛应用性[7].

设计意图：由于数学所研究的是纯粹的量，任何观察或实验的对象都必然具有特定的质的内容，因此，不能满足于对数学命题进行实际的检验，还必须从理论上去对此加以论证[7].另外，教师应明确项目学习并非从始至终在团队中进行，同时并非所有的任务都适合团队合作.于是，相较于上一环节的探究实验，该环节更关注学生独立思考、推理运算的过程，利用导数求极值的数学知识确定光程应满足的条件，进而通过严格的推理求出最速降线的曲线方程，体会数学的严谨性和广泛的应用性，培养学生逻辑推理、数学运算和数学建模等数学学科核心素养.与此同时，结合约翰·伯努利的的求解思路与费马光速最值原理和斯涅尔定律等科学原理，以数学史料和其他学科的联系来体现数学的文化性，亲历数学曲折的创造过程，体会数学家们勇于探索、追求真理的精神.

环节4：虚拟验证，技术制作

问题2-5：我们发现最速降线是具体存在的并且明确了其参数方程，传统的手绘难以处理复杂的曲线，你能否试着运用技术软件绘制出最速降线呢？

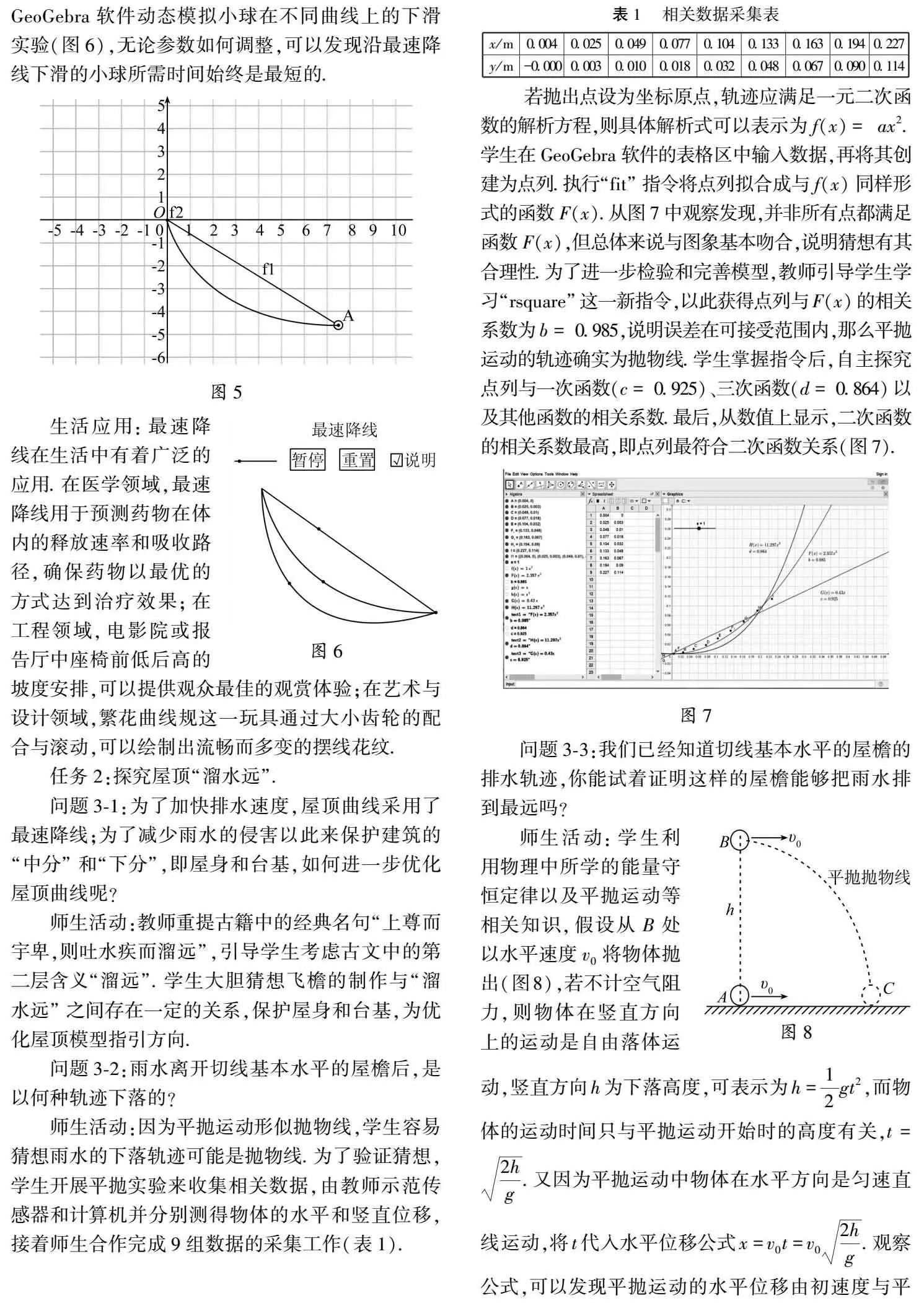
师生活动：学生查阅相关文献和程序资料后，师生共同利用GeoGebra软件绘制直线、最速降线、圆弧和抛物线等曲线.在最速降线的绘制中，教师首先引导学生对最速降线的参数方程进行转化（注意纵坐标轴改变，y取负值），转化为xy=θ-sinθcosθ-1，R=xθ-sinθ.于是，教师逐步拆解并详细解释程序，学生按照提示在GeoGebra指令栏中输入“θ=x（描点（x（A）/y（A）（cos（x）-1）=x-sin（x）））”，求出θ的值；再输入“R=x（A）/（θ-sin（θ））”，求出R的值；进而绘制出最速降线（图5）.随后，教师利用GeoGebra软件动态模拟小球在不同曲线上的下滑实验（图6），无论参数如何调整，可以发现沿最速降线下滑的小球所需时间始终是最短的.

生活应用：最速降线在生活中有着广泛的应用.在医学领域，最速降线用于预测药物在体内的释放速率和吸收路径，确保药物以最优的方式达到治疗效果；在工程领域，电影院或报告厅中座椅前低后高的坡度安排，可以提供观众最佳的观赏体验；在艺术与设计领域，繁花曲线规这一玩具通过大小齿轮的配合与滚动，可以绘制出流畅而多变的摆线花纹.

设计意图：在之前的科学实验中我们能够判断小球下滑的快慢，但并未精确求出小球下滑所需的时间.考虑到时间求解的复杂性，利用技术软件进一步佐证结论.GeoGebra技术软件辅助最速降线的项目学习，为学生提供“再创造”的环境，将圆弧、圆锥曲线等曲线图象可视化，加强了学生对旧知的动手操作与合作体验，体会深层的数学思想；通过对最速降线化简与绘制的过程，体会知识生成与“微创造”的过程.而教师利用GeoGebra制作演示动画，再现并验证科学实验的实验结果，使其更具说服力.而最速降线的生活应用的融入，正是揭示了数学对科学、工程与艺术等其他学科发展的影响，加深对数学的文化价值的理解.

任务2：探究屋顶“溜水远”.

问题3-1：为了加快排水速度，屋顶曲线采用了最速降线；为了减少雨水的侵害以此来保护建筑的“中分”和“下分”，即屋身和台基，如何进一步优化屋顶曲线呢？

师生活动：教师重提古籍中的经典名句“上尊而宇卑，则吐水疾而溜远”，引导学生考虑古文中的第二层含义“溜远”.学生大胆猜想飞檐的制作与“溜水远”之间存在一定的关系，保护屋身和台基，为优化屋顶模型指引方向.

问题3-2：雨水离开切线基本水平的屋檐后，是以何种轨迹下落的？

师生活动：因为平抛运动形似抛物线，学生容易猜想雨水的下落轨迹可能是抛物线.为了验证猜想，学生开展平抛实验来收集相关数据，由教师示范传感器和计算机并分别测得物体的水平和竖直位移，接着师生合作完成9组数据的采集工作（表1）.

若抛出点设为坐标原点，轨迹应满足一元二次函数的解析方程，则具体解析式可以表示为f（x）=ax2.学生在GeoGebra软件的表格区中输入数据，再将其创建为点列.执行“fit”指令将点列拟合成与f（x）同样形式的函数F（x）.从图7中观察发现，并非所有点都满足函数F（x），但总体来说与图象基本吻合，说明猜想有其合理性.为了进一步检验和完善模型，教师引导学生学习“rsquare”这一新指令，以此获得点列与F（x）的相关系数为b=0.985，说明误差在可接受范围内，那么平抛运动的轨迹确实为抛物线.学生掌握指令后，自主探究点列与一次函数（c=0.925）、三次函数（d=0.864）以及其他函数的相关系数.最后，从数值上显示，二次函数的相关系数最高，即点列最符合二次函数关系（图7）.

问题3-3：我们已经知道切线基本水平的屋檐的排水轨迹，你能试着证明这样的屋檐能够把雨水排到最远吗？[TPZWZ-8a.TIF;Z1，Y][TS（1][JZ]图8[TS）]

师生活动：学生利用物理中所学的能量守恒定律以及平抛运动等相关知识，假设从B处以水平速度v0将物体抛出（图8），若不计空气阻力，则物体在竖直方向上的运动是自由落体运动，竖直方向h为下落高度，可表示为h=12gt2，而物体的运动时间只与平抛运动开始时的高度有关，t=2hg.又因为平抛运动中物体在水平方向是匀速直线运动，将t代入水平位移公式x=v0t=v02hg.观察公式，可以发现平抛运动的水平位移由初速度与平抛开始时的高度共同决定；当小球抛出的方向与水平方向的夹角越小，则抛出的水平距离也就越远，从而科学解释了水平切线的檐口“溜水远”的原因.

设计意图：在探究屋顶的“吐水疾”这一任务后，以古籍中的经典名句为索引，自然过渡至探究屋顶“溜水远”，以此进一步优化最终作品.借助平抛运动的物理背景，从数学的视角发现并分析问题，到通过实验收集数据，再到利用技术软件拟合曲线，确定函数模型，发展学生数学建模和数据分析的数学核心素养.同时，教师并未止步于模型的建立，通过让学生学习操作指令获得函数的相关系数，检验与完善数学模型，养成学生的误差意识、反思能力以及严谨的科学精神.在确定轨迹后，对现实问题进一步“数学化”，证明切线基本水平的屋檐能够达成“溜水远”的效果，从感悟推理这一数学基本思想跃升至严密化的数学精神，从而使学生理解数学文化的本质.

任务3：举屋营造制作屋顶模型.

师生活动：教师引导学生思考，中国古代营造者在不知晓最速降线的情况下是如何近似拟合曲线的，并适时介绍举屋制度.举屋制度是中国传统建筑确定屋顶曲面曲度的营造方法，这一方法在宋《营造法式》中名为举折，在清工部《工程做法》中称为举架，在记述江南建筑做法的《营造法源》中谓之提栈.教师邀请匠人讲授不同时期确定屋顶曲度的营造之法，各小组选择不同的营造方法制作个性化的项目制品，彰显项目学习的核心要素“学生的发言权与选择权”[8]，发展学生对图样的识读和物化能力，感受工匠们的智慧巧思与民族的文化积累.

4项目公开评价阶段

师生活动：各小组完成模型后，教师组织学生参与古建展览会的规划与实施，提前确定活动日期并邀请学生的家庭成员.该阶段不仅仅是项目作品的展示，也应重视项目过程的公开，即让学生解释自己如何思考和完成项目，汇报并展示各项成果，包括屋顶模型、项目里程碑和汇报发言等.

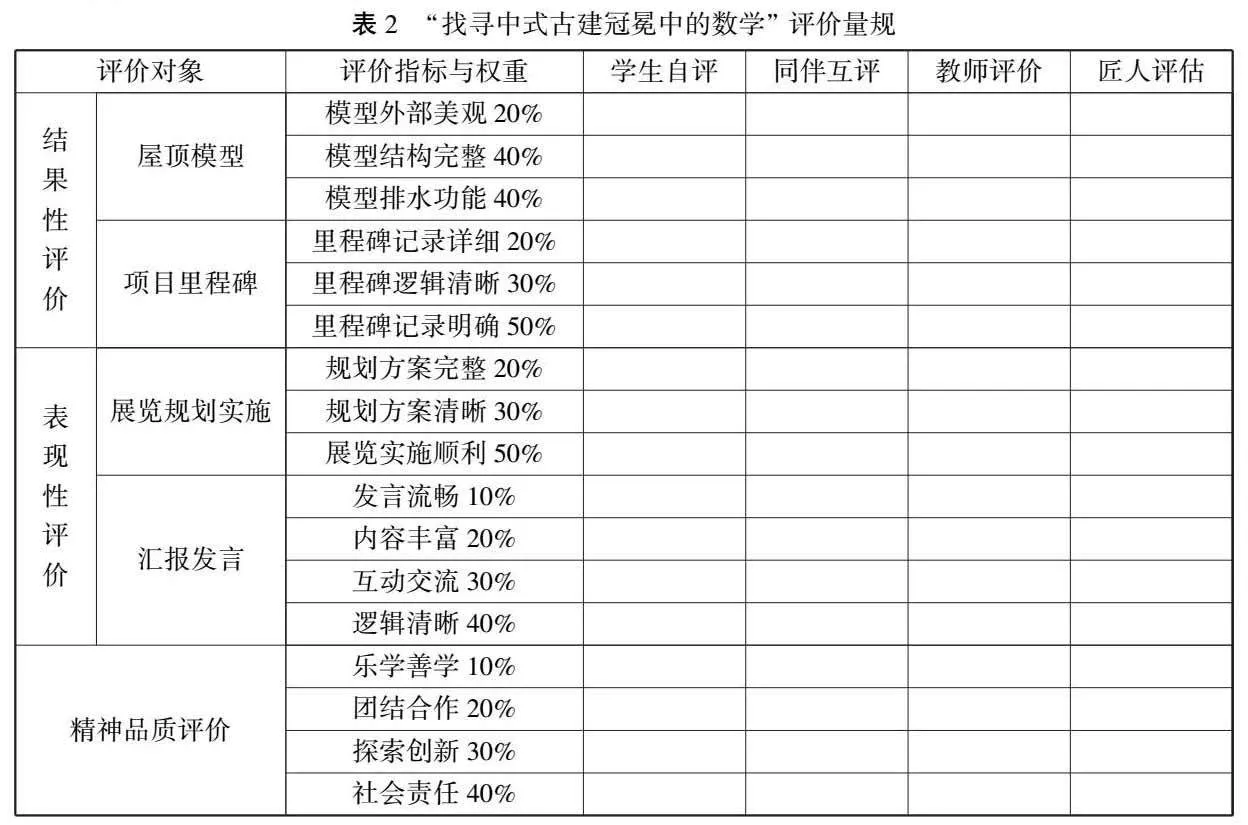
项目式学习的评估量规应紧密围绕项目主题与目标，整合学生、同伴、教师及行业匠人等多方视角，融合结果性、表现性及精神品质评价等多种方式（表2）.在结果性评价方面，以屋顶模型为例，需综合考量其外部美观度、结构完整性和排水功能等核心指标，并为各指标合理分配权重.通过学生自评、同伴互评、教师评价及匠人评估，确保评估的全面性和公正性.基于这一评价量规的持续追踪与即时反馈，学生个体及团队能够不断优化项目方案，促进成长性思维的培养.同时，教师与匠人也能据此提供更为精准的个性化指导，构建相互支持的项目文化氛围.

参考文献

[1]马俊海，张维忠.美国数学教育工程转型的缘起、进展与启示[J].浙江师范大学学报（自然科学版），2023，46（02）：227-234.

[2]张辉蓉，冉彦桃.STEAM教育理念落地：数学文化项目学习模式构建及案例开发[J].中国电化教育，2020（07）：97-103.

[3]赵千惠，张维忠.STEAM教育理念下数学拓展课教学设计研究[J].浙江师范大学学报（自然科学版），2024，47（02）：234-240.

[4]张维忠，林梦奇.基于STEAM理念的数学文化项目式学习案例开发：以“神奇的多面体”为例[J].中小学课堂教学研究，2023（07）：1-7.

[5]夏雪梅.项目化学习设计：学习素养视角下的国际与本土实践[M].北京：教育科学出版社，2021：1.

[6]郑毓信.数学方法论入门[M].杭州：浙江教育出版社，2006：93.

[7]吴佩萱.“最速降线”问题：数学史上最激动人心的一次公开挑战[J].数学通报，2006（05）：42-44.

[8]美国巴克教育研究院项目式学习计划.项目式学习指导手册：每个教师都能做PBL（中学版）[M].潘春雷，陆颖，译.北京：中国人民大学出版社，2023：61.

作者简介

张维忠（1964—），男，甘肃天水人，教授、博士生导师;主要从事数学课程与教学论研究.

胡姣灵（2000—），女，浙江宁波人，硕士研究生;主要从事数学课程与教学论研究.