数形结合，巧判全等

几何是初中数学的重要内容，对培养学生的逻辑推理、空间想象等数学素养有着重要作用。在实际教学中，学生容易混淆全等的概念和判定方法，对“两条边夹一个角”的判定条件理解得不够透彻，难以举一反三、灵活运用。因此，如何帮助学生真正理解全等三角形判定的本质，提高学生发现、提出并解决几何问题的能力，是每一位数学教师值得思考和探索的问题。

一、教材分析

人教版八年级上册数学教材第十二章专门讲述全等三角形，首先引入全等图形的定义，继而从三角形全等的充要条件出发，引出边角对应相等的概念，最后通过学生动手操作得出“边、角、边”（SAS）判定全等三角形的方法，并用经典例题加以巩固。

二、学情分析

八年级学生已具备一定的几何基础，能根据三角形全等的定义判断两个三角形是否全等，对应用三角形全等性质解决一些简单问题也有初步经验。但部分学生对边、角在全等三角形中的对应关系还不够清晰。另外，在运用已学判定方法解决几何问题时，学生往往不能很好地将抽象的判定规则与具体的问题情境结合起来。

三、教学目标

（一）会用数学的眼光观察现实世界

1.识别日常生活中的全等图形，特别是全等三角形。

2.培养从具体实物中抽象出几何关系的能力。

3.发展空间想象能力，增强几何直观能力。

（二）会用数学的思维思考现实世界

1.运用逻辑推理分析全等三角形的判定条件。

2.培养通过举反例否定命题的批判性思维。

3.发展类比推理和归纳概括的数学思维方法。

（三）会用数学的语言表达现实世界

1.准确使用数学术语描述全等三角形的概念和性质。

2.用简洁清晰的数学语言表述SAS判定定理。

3.培养用数学符号和图形表达几何关系的能力。

四、教学重难点

（一）教学重点

1.理解全等三角形的概念，明确边角对应相等的关系。

2.在操作探究中归纳SAS全等三角形判定定理，理解判定的充分性。

3.能应用SAS的判定初步解决一些简单的几何问题。

（二）教学难点

1.“两边夹角”对应关系的建立，尤其是探究活动中两组夹角的对应。

2.对SAS判定条件的理解，特别是两边和夹角的选取对结论成立的关键作用。

3.举一反三，学会从多角度思考全等三角形的判定，并能应用多种方法解题。

五、教学过程

（一）创设情境，引入新知

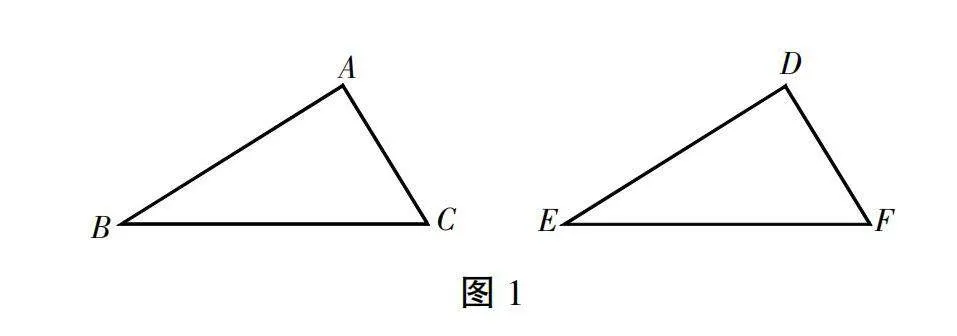
师：同学们，上节课我们学习了全等三角形的定义和性质，大家还记得吗？现在老师有两张三角形的图片（如图1所示），你们仔细观察一下，这两个三角形有什么关系？

生1：它们看起来形状和大小都是一样的。

师：没错，这两个三角形实际上是全等的。那大家思考一下，我们怎样判断两个三角形全等呢？

生2：要看它们的边长和角度是不是分别相等。

师：很好！如果两个三角形的三条边和三个角都分别相等，那它们就是全等的。我们把这个结论叫做全等三角形的性质。大家看板书，若△ABC≌△DEF，则有三组边分别相等，三组角也分别相等。这些边怎么对应，角又怎么对应呢？

生3：应该是AB对应DE，BC对应EF，AC对应DF；∠A对应∠D，∠B对应∠E，∠C对应∠F。

师：回答得非常准确！这种对应关系体现了全等图形之间元素是一一对应的。那么反过来，如果两个三角形有三组边和三组角分别相等，我们能说它们全等吗？

生：可以，因为这和全等三角形的性质是一样的。

师：大家的思路很好！我们把它叫做全等三角形的判定，它与性质是互逆的关系。可见，判定两个三角形全等需要六组条件，每组条件写出来（板书边角符号）都比较复杂。同学们想一想，我们能不能减少一些条件，用最少的条件来判定两个三角形全等呢？

生：六个条件太多了，应该可以减少一些，好像三个条件就可以……

师：看来同学们已经有了一些思路，这节课我们就来探究全等三角形判定的条件，看看到底哪几个条件可以简洁地判定两个三角形全等，这既是本节课的重点，也是难点所在，需要大家积极动脑筋、动手操作、勇于质疑，在探究中感悟。让我们一起走进三角形全等判定的世界吧！

（设计意图：本环节通过情境导入，激发学生探究三角形全等判定条件的兴趣。教师先呈现两个全等三角形的图片，引导学生回顾上节课学习的全等三角形的定义，进而思考如何判定两个三角形全等。学生在回顾中复述出全等三角形“三边三角”分别相等的性质，并在教师的引导下明确了边角对应相等的关系。教师进一步追问性质的逆命题能否成立。学生经过思考给出肯定答复，从而自然引出全等三角形的判定问题。）

（二）探究发现，构建模型

师：同学们，根据刚才的讨论，我们尝试从最少的条件入手，看能不能判定两个三角形全等。大家思考一下，如果只有一个条件，会有几种情况？

生：两种。一种是一条边对应相等，另一种是一个角对应相等。

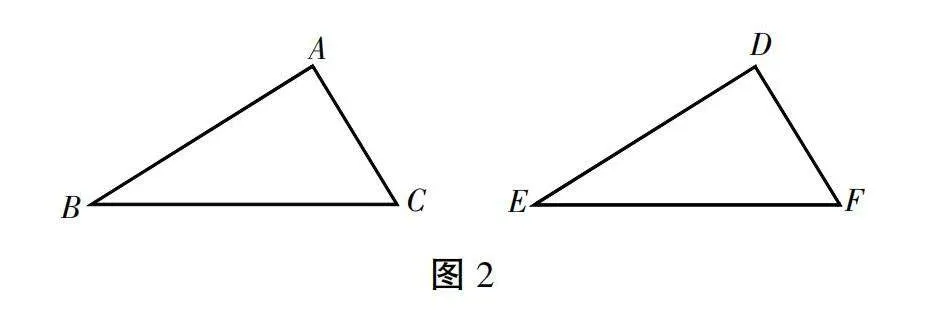
师：很好，我们先来看第一种情况。（教师在黑板上画出两个三角形，如图2所示）大家观察，如果我们只知道△ABC和△DEF有一组对应边相等，如AB=DE，请问这两个三角形全等吗？

生：不一定，除了AB和DE相等，其他边和角的关系不确定，所以三角形的形状和大小可能不同。

师：对，光有一组对应边相等还不能判定全等。我们可以用刚才学过的方法，列出反例。请同学们拿出三角板，在AB边的两端各拿一个顶点比画，看能不能画出形状不同的三角形。

（学生操作）

生1：我画出了一个钝角三角形。

生2：我画的是直角三角形，和他的不一样。

师：看来大家都找到了反例。（展示学生的三角板）这说明只有一组对应边相等，无法判定两个三角形全等。我们再看第二种情况，一个角相等行不行呢？请同学们还是用三角板，在给定角的两边比画。

生：只固定一个角，另外两个顶点可以随意移动，画出的三角形有很多种，它们肯定不全等。

师：没错，单一个角相等也不行。我们把结论写在黑板上（板书：一组对应边相等或一组对应角相等，都不能判定两个三角形全等）。这个过程就是我们常说的“举反例”，即找到符合条件但结论不成立的例子，从而否定原命题。

师：由于一个条件不够，我们再来看两个条件的情况。同学们讨论一下，两个条件会有哪几种组合？

生：我们组觉得，第一种是两组对应边相等，第二种是两组对应角相等，第三种是一组对应边和一组对应角相等。

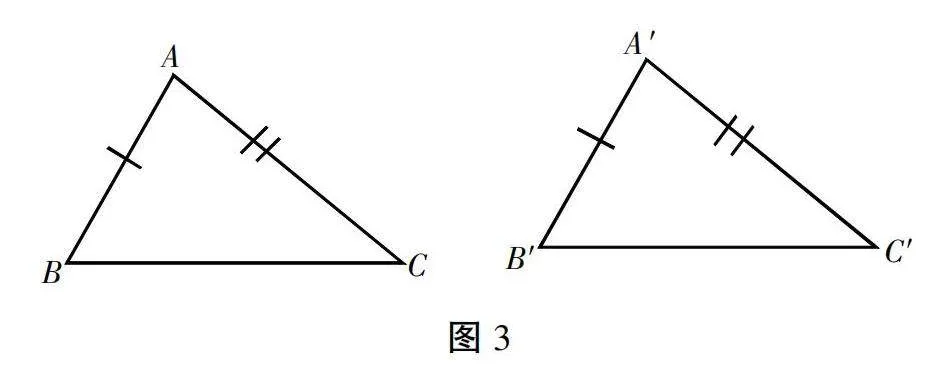
师：总结得很全面。我们逐个分析，先看两组对应边相等的情况。（出示图3）大家观察，这两个三角形的AB和A′B′相等，AC和A′C′也相等，请问这样能确定它们全等吗？请拿出圆规，以A和A′为圆心，AB为半径画两个圆弧，想象一下BC连接点的位置。

生：我发现BC的位置可以在圆弧上任意选取，所以另一个顶点的位置不确定，两个三角形不一定全等。

师：用圆规画出的图像非常直观地反映了这一点。（展示学生圆规作图）可见两组对应边相等也不能判定全等。我们再看两组对应角相等，请同学们比较自己的两个三角板，它们的两个内角分别相等，但边长能任意变化，对吗？

生：对，角相等但边不等时，两个三角形的形状相似但大小不同，不能判定全等。

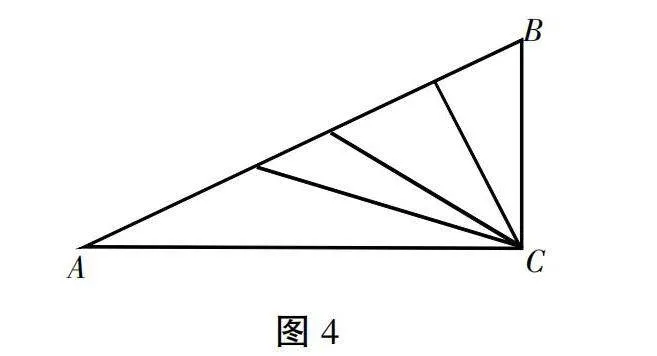
师：最后一种情况是一边一角，这需要同学们思考一下。（出示图4）如果我们固定AC和∠BAC，BC的长度还能任意变化吗？

生：BC还可以随意伸缩，改变BC的长度，所以不能确定另一个三角形。

师：对，你们分析得很准确。这说明一边一角也不行。现在我们可以得出结论了。（板书：两组对应边相等、两组对应角相等或一边一角对应相等，都不能判定两个三角形全等）

师：刚才我们分别举例说明了一个条件、两个条件不足以判定全等，背后的根本原因是什么呢？大家再思考一下。

生：我觉得是因为限定的条件不足，没有完全确定三角形的形状和大小，所以可能画出不同的三角形。

师：只有完全确定三角形的形状和大小，才能确定全等，这启示我们在探索全等判定时，要考虑所给条件能否唯一确定三角形。这也是探索的突破口。

师：三个条件的情况就留给大家课后思考了，下节课我们再来分享。现在请同学们梳理一下本节课的探究过程和方法，看看你有什么收获和感悟。

（设计意图：引导学生用类比推理和归纳概括的方法，逐步探究“一个条件”和“两个条件”判定三角形全等的可能性。在探究过程中，教师启发学生用反例说明判定的不充分性，并指导学生通过三角板操作、圆规作图等直观演示加深对反例的理解。尤其在总结“两个条件”的不同组合时，学生分工合作，逐一列举、分析，体现了归纳推理能力的提升。最后教师引导学生对探究过程进行反思，是学生能较好地概括出判定三角形全等条件选取的关键所在，并对“一个条件”和“两个条件”的情况形成系统认识。）

六、教学反思

1.动手操作与几何推理的结合还不够紧密。虽然安排了折叠、拼接等动手活动，但探究活动偏重于现象感知，对背后的数学原理挖掘不深。

2.习题设计的梯度有待优化。教师可适当补充一些开放性问题，鼓励学生提出多种解法，同时要加强与实际生活的联系，让学生感受全等知识的应用价值。

总之，几何教学要在夯实知识基础的同时，着力培养学生的空间直观、逻辑推理等数学素养。教师应积极创设有利于学生主动探究、合作交流的课堂情境，引导学生在动手实践中感悟几何本质，在问题解决中体验数学思想，不断提升学生运用数学知识的意识和能力。这是一个长期的过程，需要教师在反思中不断优化教学，让学生真正成为几何学习的主人。

（作者单位：青海省西宁市第七中学）

编辑：温雪莲