复合材料小尺寸不规则孔隙随机分布算法

摘 要：以碳纤维/环氧树脂复合材料中的孔隙为研究对象，建立一种可以生成小尺寸不规则孔隙的随机分布算法。首先利用Matlab软件对复合材料的微观形貌图像进行处理，以获取小尺寸不规则孔隙的尺寸分布统计数据。然后以该统计数据为依据，采用改进的邻点融合法，通过C++编程建立小尺寸不规则孔隙随机分布算法。最后将孔隙微观形貌图和随机分布算法生成的孔隙分布图进行对比分析，结果表明本文算法生成的孔隙与实际孔隙的形状和分布基本相同，证明了小尺寸不规则孔隙随机分布算法的有效性和合理性。

关键词：复合材料；小尺寸不规则孔隙；随机分布算法

中图分类号：TB332" " 文献标识码：A" "文章编号：1007 - 9734 （2024） 02 - 0046 - 06

0 引 言

由于复合材料制备工艺的特殊性，在固化过程中会在其内部形成各种各样的孔隙。国内外众多学者的研究表明，孔隙会对复合材料的物理性能和力学性能产生不利影响［1］，孔隙率和孔隙形貌特征（如形状、尺寸和分布）都会对复合材料的力学性能产生不同影响［2，3］。

孟欣等［4］总结了国内外有关孔隙对纤维增强复合材料不同力学性能的研究，认为孔隙对纤维增强复合材料的层间剪切、拉伸、压缩和弯曲强度以及断裂韧性和疲劳寿命影响较大。刘钧天等［5，6］针对T800级碳纤维/环氧复合材料，研究了各项工艺参数对孔隙率、孔隙分布的影响以及孔隙率、孔隙特征对层压板各项力学性能的影响，研究结果表明固化压力对孔隙率的产生有着决定性的影响，孔隙率对T800级碳纤维/环氧复合材料层压板的拉伸强度、压缩强度、剪切强度及冲击后压缩强度均会产生影响，但对各项力学性能的影响程度和变化趋势不一。Srinivasulu等［7］通过有限元建模方法研究了球形孔隙对不连续纤维增强复合材料有效弹性模量的影响，研究结果表明有效拉伸模量和泊松比会随着孔隙率的增大而降低，同时研究结果表明孔隙率对有效弹性性能的影响大于孔隙纵横比和尺寸分布的影响。Nisrin［8］通过实验分别研究了孔隙率对复合材料层合板在静态和疲劳状态下的I型破坏、II型破坏的影响，结果显示断裂能释放率随着孔隙率的不断增大而不断减小。Sanja等［9］通过实验研究了孔隙对各项同性碳纤维增强复合材料力学行为的影响，研究结果表明孔隙会导致复合材料层合板的刚度、强度和疲劳寿命减小，也使层合板的裂纹密度增加。肖鹏等［10］对碳纤维增强复合材料的孔隙率、孔隙分布和形貌特征进行了研究，结果表明固化压力不足和袋内真空不合适是导致复合材料内部孔隙产生的主要原因，同时孔隙分布存在着随机性且孔隙形貌与孔隙率之间存在一定的联系。Arthur等［11］通过低速冲击实验研究了碳纤维/环氧树脂复合材料层合板低速冲击时孔隙对其裂纹扩展的影响，结果表明孔隙是裂纹产生的初始点，会导致基体裂纹扩展，但同时孔隙对分层破坏的扩展有一定抑制作用。

众多研究表明：碳纤维增强复合材料中孔隙无法完全避免，且孔隙的存在（孔隙率、孔隙形状、孔隙尺寸和孔隙分布）对复合材料的各项性能会产生较大影响。因此，本文以碳纤维增强复合材料中的小尺寸不规则孔隙为研究对象，采用改进的邻点融合法，通过C++编程建立小尺寸不规则孔隙的孔隙随机分布算法，为后续通过有限元方法研究孔隙对碳纤维复合材料力学性能的影响建立模型和基础。

1 孔隙微观特征提取

碳纤维复合材料中孔隙的形状、尺寸会随着孔隙率的不同而发生变化。通过观察复合材料的SEM（Scanning Electron Microscope，SEM）图像以及综合相关文献，可以将碳纤维复合材料中的孔隙分为三类：规则孔隙［8］（完全处于基体中）、小尺寸不规则孔隙［12］（完全处于基体中）以及大尺寸不规则孔隙［13］（处于纤维之间），如图1所示。

规则孔隙是在复合材料制造过程中挥发性物质产生或空气未完全排除而形成的气泡，形状主要为球形［14］，不规则孔隙则是形状不规则的柱形孔洞，一般与纤维方向平行［15］。

小尺寸不规则孔隙完全处于基体中，且单个孔隙的面积各不相同。为了保证小尺寸不规则孔隙随机分布算法的合理性和有效性，孔隙随机分布算法生成的孔隙等效半径分布，应与实际孔隙等效半径分布统计等价。因此，需要对复合材料SEM图形进行处理，以获取实际孔隙等效半径分布。

使用Matlab软件对图1（b）中的复合材料SEM图像进行处理，一般步骤如下：

（1）导入原始的复合材料SEM图像；

（2）对导入的SEM图像进行增强处理，然后将其转换成灰度图像；

（3）采用直方图均衡化方法对图像质量进行改善；

（4）通过迭代法选取适当阈值，将灰度图像二值化处理，转化成二值图像；

（5）对二值图像进行数学形态学处理；

（6）将每个孔隙的像素面积转换成真实孔隙的等效半径；

（7）绘制孔隙等效半径直方图，并输出所有孔隙的等效半径。

处理后的复合材料SEM图像如图2所示。从图中可以看出：经过一系列处理（灰度处理、二值化处理、形态学处理以及手动处理等）后，复合材料中孔隙的形貌特征十分清楚，这对于统计孔隙的等效半径分布十分有利。

从图1（b）和图2中可以看出孔隙形状是不规则的，文献［16］针对不规则孔隙提出了等效直径的概念，将不规则孔隙通过等效直径公式转化成相同面积的圆，等效直径的公式如下：

[Deq=4Aπ]" " " " " " " " " " " " " " " " " " " " " " " " " " " " （1）

[Req=Deq/2]" " " " " " " " " " " " " " " " " " " " " " " " " " " " "（2）

其中A为孔隙面积，Deq为孔隙等效直径，Req为孔隙等效半径。最终通过Matlab软件获得的复合材料中小尺寸不规则孔隙的等效半径如表1所示。

2 小尺寸不规则孔隙随机分布算法

2.1" 平稳随机介质模型

复合材料是由两种或两种以上物质组合而成的多相固体材料，属于非均匀介质，因此可以使用平稳随机介质模型对其进行描述。Ikelle等在文献［17］中已经指出利用椭圆自相关函数构造的随机介质模型可以很好地模拟小尺度的非均匀性。因此本文以密度ρ（x， y）作为介质参数，使用椭圆自相关函数来构造平稳随机介质模型，其步骤如下所示。

步骤1" 选择高斯型自相关函数：

[ϕx，y=e-（x2a2+y2b2）]" " " " " " " " " " " " " " " " " " " " " " " （3）

步骤2" 计算自相关函数的二维离散傅里叶变换：

[φx，y=x=0m-1y=0n-1ϕx，ye-2πi（uxm+vyn）]" " " " " " " " " "（4）

步骤3" 在区间[-π， π]上随机生成服从均匀分布的二维随机场θ（u， v），并计算随机功率谱：

[su，v=φx，yei·θu，v]" " " " " " " " " " " " " " " " "（5）

步骤4" 计算随机功率谱的二维离散傅立叶逆变换：

[σ'x，y=1mnu=0m-1v=0n-1su，ve2πi（uxm+vyn）]" " " " " " " （6）

步骤5" 计算σ'（x， y）的均值及方差：

[μ=Eσ'x，y]" " " " " " " " " " " " " " " " " " " " " " " " （7）

[d2=Eσ'x，y-μ]" " " " " " " " " " " " " " " " " " " "（8）

步骤6" 产生均值为0、方差为ε2，且以[ϕ（x，y）]作为自相关函数的随机扰动σ（x， y）：

[σx，y=εdσ'（x，y）-μ]" " " " " " " " " " " " " "（9）

步骤7" 构造的平稳随机介质模型为：

[ρ（x，y）=ρ01+σ（x，y）]" " " " " " " " " " " " " " " "（10）

2.2" 随机孔隙模型

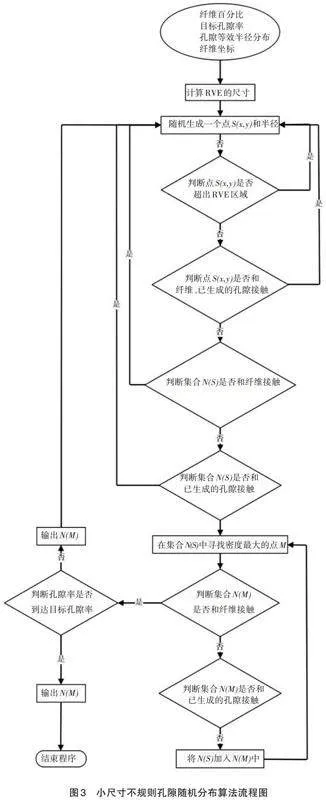
平稳随机介质模型并不能直接生成孔隙，需要改造成随机孔隙模型后才能生成不规则孔隙。文献［18］中提出了一种可以生成随机孔隙的邻点融合法，但有明显的不足之处：生成的每个孔隙面积都相同，而这显然和复合材料孔隙的实际情况不相符合。本文针对邻点融合法的不足之处进行改进，结合RVE（Representative Volume Element）模型，提出了一种小尺寸不规则孔隙的随机分布算法，步骤如下。

步骤1：输入纤维百分比、目标孔隙率、孔隙等效半径分布以及RVE包含的所有纤维的中心坐标。

步骤2：计算RVE尺寸，确定目标区域的长度和宽度，并将整个RVE作为生成孔隙的区域。

步骤3：随机生成一个点S（x， y）和孔隙半径r，若S超出目标区域，则重新生成。

步骤4：判断点S是否与纤维接触。若与纤维接触，回到步骤3；若不接触，则进行步骤5。

步骤5：检测点S是否和已生成的孔隙接触。若接触，则回到步骤3。

步骤6：将以点S为圆心，半径为r的圆上的所有点的集合记为N（S）。判断集合N（S）是否接触到纤维。若接触则回到步骤3。

步骤7：判断集合N（S）是否和已经生成的孔隙接触。若接触则回到步骤3。

步骤8：寻找密度最大的点M，即

[ρ（M）=maxm∈NSρ（m）=ρ（x，y）]" " " " " " " " " " " （11）

步骤9：把以点M为圆心、r为半径的圆上所有点的集合记为N（M）。判断集合N（M）是否和纤维接触。若不接触，则进行步骤10。若接触，则进行步骤11。

步骤10：判断集合N（M）是否和已经生成的孔隙接触。若不接触，则将集合N（M）加入N（S）中，然后回到步骤8。若接触，则进行步骤11。

步骤11：检测已生成孔隙的当前孔隙率是否等于目标孔隙率。若小于目标孔隙率，则进行步骤12；若大于目标孔隙率，则将加入N（S）中的最后一个集合N（M）的孔隙半径r值减小到等于目标孔隙率为止，然后进行步骤12。

步骤12：输出N（S）。若当前孔隙率小于目标孔隙率，则终止程序。

小尺寸不规则孔隙随机分布算法的流程如图3所示。

3 结果及分析

根据图1（b）中复合材料中孔隙的分布情况可知，小尺寸不规则孔隙随机分布算法需要满足如下要求：

（1）随机算法生成的孔隙和纤维之间不能交叉。

（2）随机算法生成的孔隙只能存在于基体中且分布是随机的。

（3）随机算法生成孔隙的半径分布要与实际孔隙等效半径分布统计等价。

为了验证本文小尺寸不规则孔隙随机分布算法的合理性和有效性，通过随机分布算法生成孔隙率分别为0.6%、0.8%以及1%的三种孔隙模型（如图4所示）。从图中可以看出，三种孔隙率的模型中孔隙都满足了如下要求：孔隙不与纤维交叉、孔隙分布随机、孔隙只存在于基体中，证明了本文算法的合理性。

从图4中也可以看出，当单个孔隙的面积较小时，孔隙形状基本接近圆形；而随着单个孔隙面积的增大，孔隙则开始出现不规则形状。这种变化趋势与真实孔隙形貌的变化趋势基本相同，也证明了本文算法的合理性。

从图4（c）中可以看出，当孔隙率为1.0%时，尽管此时孔隙率已经较大（孔隙率小于2%的复合材料为合格的材料）且孔隙数目也较多，但图中所有孔隙的形状都没有重复，说明了本文算法的有效性。

图5为孔隙率为2.0%时，包含小尺寸不规则孔隙的RVE模型图进行一系列处理后的二值图像（黑色区域为孔隙）。将图5和图2进行对比分析，可以发现两幅图的二值图像基本相似，孔隙分布比较离散，孔隙形状大部分为无规则状，且全部孔隙中小面积孔隙居多。从而说明了本文中小尺寸不规则孔隙随机分布算法的合理性和有效性。

4 结 论

（1）本文以碳纤维/环氧树脂复合材料中的孔隙为研究对象，建立一种可以生成小尺寸不规则孔隙的孔隙随机分布算法。对比分析表明本文的算法具有有效性和合理性。

（2）本文算法生成的孔隙与真实孔隙形貌相似。孔隙面积较小时孔隙形状近似为圆形，孔隙面积较大时孔隙形状为不规则形状，且全部孔隙形状没有重复。

（3）本文的小尺寸不规则孔隙随机分布算法可以通过改变参数生成包含各种类型孔隙的RVE模型，为后续研究孔隙率、孔隙分布、孔隙尺寸及孔隙形状对复合材料力学性能的影响提供理论基础和研究模型。

参考文献：

［1］付宗周.碳纤维复合材料孔隙率超声检测与评价［J］.无损检测，2023，45（9）：33-38，73.

［2］张阿樱，张东兴，李地红，等.碳纤维/环氧树脂层压板的孔隙问题［J］.宇航材料工艺，2011（3）：16-19.

［3］朱洪艳，李地红，张东兴，等.碳/环氧复合材料层压板孔隙的形态研究［J］.材料科学与工艺，2010，18（5）：657-661.

［4］孟欣，刘伟.孔隙对纤维增强复合材料力学性能影响的研究进展［J］.居业，2023（5）：207-211.

［5］刘钧天，陈萍，闫超，等.不同自动铺丝工艺参数对T800级碳纤维/环氧复合材料孔隙率的影响研究［J］.航空制造技术，2023，66（3）：114-118，124.

［6］刘钧天，陈萍，于晶晶，等.孔隙率对环氧/T800级碳纤维复合材料力学性能影响［J］.工程塑料应用，2022，50（10）：101-106.

［7］SRINIVASULU G，VELMURUGAN R，JAYASANKAR S.Influence of void microstructure on the effective elastic properties of discontinuous fiber-reinforced composites［J］. Journal of Composite Materials， 2015，49（22）：2745-2755.

［8］ABDELAL N R.Effects of voids on delamination behavior under static and fatigue mode I and mode II［D］.Dayton， University of Dayton，2013.

［9］SANJAY S，GAMSTEDT E K，FREDRIK E，JANIS V. Effects of voids on quasi-static and tension fatigue beha-viour of carbon-fibre composite laminates［J］.Journal of Composite Materials， 2015，49（17）：2137-2148.

［10］肖鹏，刘卫平，刘奎，等.碳纤维复合材料孔隙分布及形貌分析研究［J］.玻璃钢/复合材料，2016，（2）：62-66.

［11］ARTHURS B，BULL D J，ARUMUGAM V，HAMBERS A R，SANTULLI C.Porosity effect on residual flexural strength following low energy impact of carbon fibre composites［J］. Polymers and Polymer Composites ，2015，23（4）：205-212.

［12］CECILIA G，FERNAND E.Determining a representative volume element capturing the morphology of fibre rein-forced polymer composites［J］.Composites Science and Technology， 2007，67：766-775.

［13］LIU H L，CUI H T，WEN W D，SU X M，KANG H， CARLOS E P.The effect of voids on the quasi-static tensile properties of carbon fiber/polymer-laminated composites［J］.Journal of Composite Materials，2017，52（15）：1997-2015.

［14］张冬梅，叶金蕊，刘奎，等.孔隙微观特征影响CFRP力学性能的细观综述［J］.复合材料学报，2013，30（S1）：118-123.

［15］SCOTT A E，SINCLAIR I，SPEARING S M，MAVROGOR-DATO M N，HEPPLES W. Influence of voids on damage mechanisms in carbon/epoxy composites determined via high resolution computed tomography［J］.Composites Science and Technology， 2014，90：147-153.

［16］YOUSSEF K H，LEVENT A，ALTAN M C.Three-dimensional features of void morphology in resin transfer molded composites［J］.Composites Science and Tech-nology，2005，65：1306-1320.

［17］IKELLE L T，YUNG S K，DAUBE F.2-D random media with ellipsoidal autocorrelation functions［J］.Geophysics， 1993，58（9）：1359-1372.

［18］奚先，姚姚，顾汉民.随机溶洞介质模型的构造［J］.华中科技大学学报（自然科学版），2005（9）：105-108.

责任编校：裴媛慧，陈 强

Random Distribution Algorithm for Small Irregular Voids in Composites

LI Bo，LING Xinru

（School of Civil Aviation，Zhengzhou University of Aeronautics，Zhengzhou 450046，China）

Abstract：This article takes the voids in carbon fiber/epoxy resin composite materials as the research object and establishes random distribution algorithm for generating small irregular voids of composites.Firstly，using Matlab to process the microstructure images of composites to obtain statistical data on size distribution of voids.Then，based on the statistical data， an improved neighbors' interfusion method is used to establish small irregular voids random distribution algorithm through C++.Finally，a comparative analysis was conducted between the micro morphology map of voids and the voids distribution map generated by the random distribution algorithm.The analysis results showed that the shape and distribution of the voids generated by the void random distribution algorithm in this paper are basically the same as those of the actual voids，proving the effectiveness and rationality of the random distribution algorithm for small and irregular voids in this paper.

Key words：composites；small irregular voids；random distribution algorithm

作者简介：李 波，男，山西运城人，博士，讲师，研究方向为固体力学、理论力学、飞机构造与设计等。