多翼离心风机气动噪声数值预测

摘 要：文章采用计算流体力学软件Fluent对多翼离心风机的内部流场进行三维的定常和非定常数值模拟，并对数值结果进行了分析。数值结果与试验结果的对比分析表明了数值模拟具有较好的准确性和可信度。随后，基于流场的计算结果进行声场的数值计算，结果表明：基于非定常流动的FW-H声压模型可获得多翼离心风机气动噪声主要噪声源在声学接收点处的噪声频谱，有助于更深层地了解声源的噪声特性以及明确噪声峰值所对应的频率段，为下一步进行有针对性的噪声控制研究提供有力的依据。

关键词：多翼离心风机；气动噪声；数值预测；FW-H声压模型

中图分类号：TH452" "文献标识码：A" " 文章编号：1007 - 9734 （2024） 02 - 0033 - 05

0 引 言

噪声与空气污染和水污染一起被列为当今世界的三大主要污染源，是工业文明危害环境的主要因素之一。一种声音之所以成为噪声是因为它会引起疲劳、不舒适，或者影响通讯，或者更极端的情况，会引起听力损失［1］。一般认为日常生活的环境噪声应不高于35dB，办公的环境噪声应不高于45dB［2］。

叶轮机械是工农业生产及人们的日常生活中应用极为广泛的机械设备，它覆盖着动力、电力、化工、冶金及机械等多个工程领域。随着世界经济的持续增长和人民生活水平的逐步提高，各种叶轮机械的保有量逐年增加，转速也越来越高，使用环境也愈加复杂，其运转噪声对工业生产以及人们日常生活的影响日趋严重。作为叶轮机械的一种，多翼离心风机以其体积小、结构紧凑、大流量系数、高压力系数及低噪声等特点在国民经济建设及人们日常生活中的使用量越来越大，使用范围也越来越广，如空调、仪器设备的通风散热、厨房吸油烟机等，并在很多特殊使用场合被公认为是一种最理想的风源设备。目前，大部分以多翼离心风机为主体的通流设备的噪声指标已完全满足国标的要求，但是相对于人们正常的生活和工作环境来说，其运转噪声仍然偏大（如厨房的吸油烟机的噪声可高达55dB—60dB［3］，工业用风机的噪声则更高）。而当下我国政府已经将环境保护列为基本国策之一，因此，针对叶轮机械开展噪声预测及噪声控制方面的研究是非常有必要的。

根据发声体以及声波传播介质的物态，可将风机的运行噪声划分为空气动力噪声、机械噪声、电磁噪声和前两者之间的耦合噪声。以某型空调离心风机为研究对象，数值模拟结果表明：蜗舌处及叶片表面压力波动幅度大，是风机的主要噪声源［4］。邓伟以某型多翼离心风机为研究对象，基于大涡模拟预测风机的远场噪声，并提出优化方案，实现了2dB的降噪［5］。李哲弘采用数值模拟与实验测量相结合的方法，研究不同叶片形状下多翼离心风机内部漩涡流动规律、形成原因以及叶片尾缘脱落涡与风机噪声的关系，提出了噪声预测公式［6］。相关研究表明［7］，气动噪声占风机运行噪声的45%以上。因此，本文以多翼离心风机为研究对象，基于大型商用CFD软件——Fluent，将成功应用于轴流风机、贯流风扇、离心风机以及飞机螺旋桨等方面中的气动噪声预测方法［8］（FW-H声压模型）应用到多翼离心风机的气动噪声数值预测中，以期获得针对多翼离心风机气动噪声的准确高效的数值预测方法。

1 基本理论

FW-H方程是非齐次的波动方程［9-10］，可以从连续方程和N-S方程中得出。其表达式如下：

[1a20∂2p∂t2-∇2p=∂2∂xi∂xjTijHf-][∂∂xiPijnj+ρuiun-vnδf+][∂∂tρ0vn+ρun-vnδf] （1）

式（1）中，[ui]是[xi]处的流体速度分量；[un]是垂直于 [f=0]的表面的流体速度分量；[vi]是[xi]处的表面速度分量；[vn]是垂直于表面的表面速度；[δf]是[δ]脉冲函数；[Hf]是海维赛德函数；[p]是远场的声压（[p=p-p0]）；从数学角度讲，[f=0]是相对于包含在一个极大的空间中的外流（[fgt;0]）来说的，在这个空间中，广义函数理论和自由格林函数可以用来进行求解，[f=0]表面相当于声源发射面，可以认为是不能渗透的物体表面或者离开物体表面的可渗透面；[ni]是指向外部区域（[fgt;0]）的单位法向量；[a0]是远场的声速；[Tij]是Lighthill应力张量，其表达式如下：

[Tij=ρuiuj+Pij-a20ρ-ρ0δij] （2）

[Pij]是压力张量，对于Stokesian流动，其表达式如下：

[Pij=pδij-μ∂ui∂xj+∂uj∂xi-23∂uk∂xkδij]" "（3）

自由来流用下标0表示。

方程（1）可以用自由格林函数（[δg4πr]）来求解。完全解包含面积分和体积分，面积分代表单级子源噪声、偶极子源噪声和部分四级子源噪声；而体积分代表面源外部区域四级子体积源的噪声。当流动是低亚音速流动且面源包含源地时，体积分的贡献就会变得很小，在Fluent中，体积分可以忽略，因此有：

[px，t=p′Tx，t+p′Lx，t]" （4）

其中，

[4πp′Tx，t=f=0ρ0Un+Unr1-Mr2dS+][" " f=0ρ0UnrMr+a0Mr-M2r21-Mr3dS]" （5）

[4πp′Lx，t=1a0f=0Lrr1-Mr2dS+][f=0Lr-LMr21-Mr2dS+][1a0f=0LrrMr+a0Mr-M2r21-Mr3dS]" （6）

式（4）—（6）中，

[Ui=vi+ρρ0ui-vi]" " " " " （7）

[Li=Pijnj+ρuiun-vn]" " " （8）

当要积分的面是不可渗透的壁面时，公式（4）右边的[p′Tx，t]和[p′Lx，t]根据各自的物理意义分别代表厚度项和载荷项。公式（5）和（6）中的平方括号项代表积分的核心在相应的延迟时间[τ]进行计算。[τ]是准时时间[t]和距观测者的距离[r]的函数，表达式如下：

[τ=t-ra0] （9）

公式（5）和（6）中带有下标的变量代表各自的矢量和单位矢量的点积。例如，[Lr=L⋅r=Li⋅ri]和[Un=U⋅n=Ui⋅ni]，其中[r]和[n]分别代表径向单位矢量和壁面法向方向的单位矢量。带点的变量代表该变量对时间的微分。

关于该积分法的适用性有以下几点说明：

① Fluent中的FW-H方程既可处理旋转面问题，又可处理静止面问题；

② [f=0]的面与物体表面或壁面重合不是必要的条件。允许可渗透的噪声源出现，这样该积分法就可以在内流中应用；

③ 当远离物面或壁面一定距离的地方出现可渗透的噪声源时，公式（5）和（6）中的积分得包含被面源包围的区域内的四级子源产生的噪声。当使用可渗透噪声面源时，需要足够好的计算网格来求解被可渗透噪声面源包围的区域内的瞬态流动。

2 数值计算

运用FW-H声压模型进行多翼离心风机气动噪声预测的主要步骤有：

（1）获得流场的定常解；

（2）获得流场的非定常解；

（3）启用FW-H声压模型，设定相关模型参数，同时指定声源和声学接收点的位置；

（4）进行非定常流场的进一步求解；

（5）求解声压信号；

（6）计算结果的后处理。

3 算 例

本文选用应用于吸油烟机中的多翼离心风机，结合上述方法进行多翼离心风机内部流场和声场的数值计算。

3.1" 流场计算

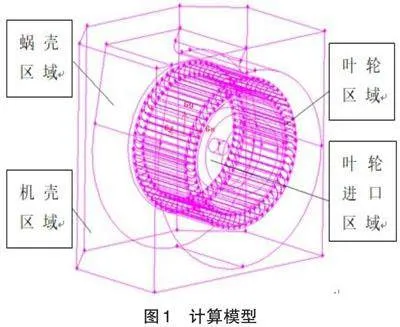
计算模型如图1所示，共分为四个区域：机壳区域（机壳与蜗壳之间的流道）、蜗壳区域（叶轮外径与蜗壳之间的流道）、叶轮区域（60个前向单圆弧非扭曲叶片之间的流道）和叶轮进口区域（进风圈与叶轮内径之间的流道）。

FW-H声压模型需要获得流场变量的时间精确解，即获得流场的非定常解，因此本文选用的旋转模型为滑移网格模型。为了有利于非定常计算的收敛，在对模型进行非定常计算之前，先对其做定常计算，待其收敛后将定常计算的结果作为非定常计算的初始化数据，而后进行非定常计算。在定常计算中，湍流模型采用标准的k-ε模型，近壁区域采用壁面函数法进行处理，离散方程采用分离隐式方法求解，压力-速度耦合采用SIMPLEC算法，湍流动能、湍流耗散率、动量方程等采用二阶迎风格式离散；在非定常计算中，Unsteady Formulation采用二阶隐式，Porous Formulation采用Superficial Velocity，压力-速度耦合采用PISO算法，压力离散采用PRESTO！算法，湍流动能、湍流耗散率、动量方程等采用二阶迎风格式离散。由于动静区域间采用了滑移网格，动静区域间的连接面只能定义为交界面（interface），计算中需要通过Fluent中的Define/Grid interface来实现动静区域间的数据交换。

3.2" 声场计算

为使非定常计算的结果有足够的频率段，本文的时间步长取为1×10-4s（计算频率范围0～5000Hz），待非定常计算出现周期性稳定的现象后，启用FW-H声压模型，指定声源的位置（叶轮、蜗壳等）和声学接收点（本文的声学接收点设定为出口中心外1m处），进行声学计算和输出，随后进行声学分析。期间，声学数据存储5000步，持续时间0.5s，叶轮旋转10圈。

4 结果分析

4.1" 流场结果分析

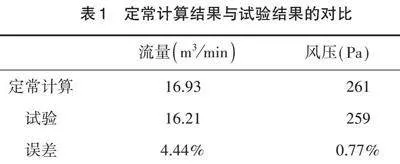
表1给出了定常计算结果与试验结果的对比情况。可以看出二者之间吻合较好（误差在+5％以内），表明了数值计算的结果是合理的，计算方法是可靠的，计算模型是可取的。

从表1中同样可以看出，数值结果对比试验测量结果偏大，产生该误差的原因主要有：建模阶段对风机的部分区域进行了简化处理，从而使得数值计算中的摩擦损失、轮阻损失和泄漏损失与试验测量结果相比偏小；建模时忽略的一些次要结构，会带来一定的误差；由于模型的复杂性以及计算条件的限制，选用的网格类型是非结构网格，精度有限，从而引起一定的误差。

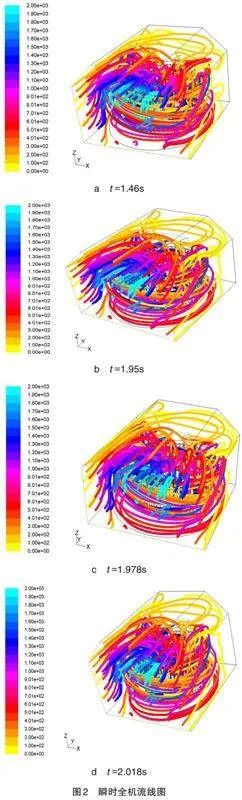
图2给出了基于非定常计算的不同时刻的全机流线图。各个时刻的流量分别为：16.87m3/min、17.01m3/min、 17.04m3/min、16.98m3/min，偏差在1%以内，且与试验所得的数值（16.21m3/min）相比，误差在6%以内，吻合较好，说明计算方法是可取的，结果是可信的。

从图2中可以看出，不同时刻的流动情况有略微的区别，与定常计算相比，非定常计算能够展现更多的流动细节，更加接近实际流动。这种不同时刻流动情况的略微不同，将导致叶轮流道中的分离涡、叶片尾迹涡、脱落的尾迹涡、蜗舌处的分离涡以及蜗壳壁面的附面层涡的生成与脱落，会随时刻发生变化。此外，涡的位置与尺度也将随时刻发生改变，都随着流动做周期性变化。

4.2" 声场结果分析

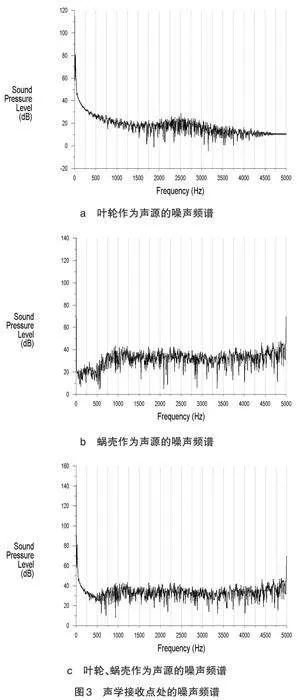
图3分别给出了叶轮、蜗壳以及同时考虑叶轮、蜗壳作为声源时，在声学接收点计算得到的噪声频谱。

从图3中可以看出，当叶轮作为声源时，在频率50Hz附近存在一个较大的峰值（约80dB），在频率2500Hz处存在一个较小的峰值（约28dB），在其余频率段，声压级无非常明显的峰值，都保持在20dB左右，其总声压级为80.85dB。当蜗壳作为声源时，整个频谱呈现宽频的特点，除了在频率5000Hz处存在一个较大峰值（约67dB）之外，在整个频率段内声压级无非常明显的差异，都保持在30dB—40dB，其总声压级为68.29dB。当叶轮和蜗壳同时作为声源时，整个频率段内基本呈现宽频特性，除了频率段的开头和结尾处存在明显的峰值外，声压级无非常明显的差异，其总声压级为81.08dB。同时，从计算结果来看，叶轮是相对最主要的气动噪声源。

5 结 论

本文采用基于非定常流动的FW-H声压模型进行多翼离心风机气动噪声的预测，结果表明：该方法不仅可以获取气动噪声主要噪声源在声学接收点处的声压级数值，还可以获取气动噪声主要噪声源在声学接收点处的噪声频谱，有助于更深层地了解声源的噪声特性以及明确噪声峰值所对应的频率段，可为下一步进行有针对性的噪声控制研究提供有力的依据。

参考文献：

［1］黄其柏.工程噪声控制学［M］.武汉： 华中科技大学出版社，1999.

［2］智乃冈.风机噪声控制技术［M］.北京： 机械工业出版社， 1985.

［3］周唯儒，覃小倩. 吸油烟机气动噪声来源及仿真分析方法综述［J］.家电科技，2021（1）：62-67.

［4］孔宣.多翼离心风机动力叶轮及排气蜗壳联合设计［D］.哈尔滨：哈尔滨工业大学，2019.

［5］邓伟.多翼离心风机的噪声预测与降噪研究［D］.上海：上海工程技术大学，2021.

［6］李哲弘.前向多叶离心通风机漩涡流动与噪声预测研究［D］.杭州：浙江理工大学，2019.

［7］熊毅.多翼离心风机气动性能与噪声优化［D］.赣州：江西理工大学，2022.

［8］闫莹，肖友洪，卢华兵，等.基于有限元法离心风机气动噪声预报研究［J］.流体机械，2022，50（11）：61-68.

［9］WILLIAMS J E，HAWKINGS D L. Sound generation by turbulence and surfaces in arbitrary motion［J］.Philosophical Transactions of the Royal Society of London Series A-Mathematical and Physical Sciences，1969，264（1151）：321-332.

［10］WILLIAMS J E，HAWKINGS D L.Theory relating to noise of rotating machinery［J］.Journal of Sound and Vibration，1969，10（1）：10-22.

责任编校：刘 燕，田 旭

Aero-acoustics Numerical Prediction of Multi-blade Centrifugal Fan

HAN Feifei

（Zhengzhou University of Aeronautics，Zhengzhou" 450046，China）

Abstract： In this paper， Fluent is applied in the 3D steady and unsteady numerical simulation of internal air flow of the multi-blade centrifugal fan， and the results are analyzed， the comparison between the numerical simulation results and the experimental results demonstrate the good accordance and the reliability of the numerical simulation. And then， aero-acoustics numerical prediction is carried out based on the result of flow field， the result demonstrates that we can obtain the frequency character in the acoustic receiving location of the dominant aerodynamic noise source of the multi-blade centrifugal fan according to the FW-H acoustic model based on the result of unsteady flow field. All above can be helpful in the research on the noise character of noise source， and make sure the frequency section which the peak value is corresponding to， in the meantime， it can offer powerful suggestion and direction for the research on the following special noise control.

Key words： Multi-blade centrifugal fan; Aero-acoustics; numerical prediction; FW-H acoustic model

基金项目：国家自然科学基金青年基金（52206059）

作者简介：韩非非，男，河南伊川人，博士，讲师，研究方向为通风机内部流场数值仿真、噪声计算及控制、风力发电机风轮设计及数值计算。