初中数学错题成因及解题教学改进策略

摘要：在初中数学教学中，教师可通过分析学生解题过程中常见的错题成因，并利用例题还原错误解答过程，加深学生对所学知识的理解.在解题过程中，采用问题解析式解题策略，不但能够提高学生分析问题和解决问题的能力，而且可促使教师改进教学策略，提高教学效果.

关键词：初中数学；错题成因；解题教学；教学策略

中图分类号：G632文献标识码：A文章编号：1008-0333（2024）26-0027-03

初中数学是学生数学学习的关键阶段，学生不仅要熟练掌握数学概念，而且要培养逻辑思维和问题解决能力.数学解题能力是帮助学生掌握概念、形成逻辑思维能力的基础.然而，许多学生由于经验缺乏、思维惯性、缺少指导等原因，在解题过程中常常面临各种困惑，导致其解题能力无法提升.因此，对于初中数学解题中的常见错题成因进行深入研究，可提升学生的解题能力和数学思维能力，优化教师解题教学方法，提高数学教学效果.

1学生解题过程中常见的错题成因

1.1问题识别困难

在初中数学学习中，学生在解决问题时，可能难以准确理解问题要求，无法正确提取问题的关键信息.究其原因，一是学生的数学知识储备不足，对数学概念、原理理解不够透彻，导致其在问题识别过程中出现困惑；二是学生对题目中所需要解决的问题理解错误，或者未能准确把握题目中没有明确给出的关键信息；三是在学习过程中，学生可能会遇见很多类似的问题，这些问题在表述与要求上类似，但解题方法与思路略有不同.

例1已知a，b，c为三个非零有理数，若abc＜0，则aa+bb+cc的值为多少？

错误解答：利用绝对值的性质可以得到四种结果.第一种情况：原式=1+1+1=3；第二种情况：原式=-1-1-1=-3；第三种情况：原式=1+1-1=1；第四种情况：原式=1-1-1=-1.综上所述，aa+bb+cc的值为±3，±1.

在解答此题过程中，学生容易因为粗心遗漏“abc＜0”这一条件，未能准确把握题目中没有明确给出的关键信息.学生主观认为，a，b，c的符号分四种情况，一是a，b，c均为正数；二是a，b，c均为负数；三是a，b，c中有两个正数、一个负数；四是a，b，c中有两个负数，一个正数.基于此，学生可得到四种结果.在初中数学教学中，教师应该指导学生细心审题，对于题目中的任何条件都不能遗漏.

1.2策略选择困难

在初中数学解题过程中，当学生面对复杂问题时，可能缺乏解题的有效策略，从而无法准确选择解题方法，不能有效确定解题的途径和步骤，或缺乏尝试从不同角度解题的能力.究其原因，一是学生可能对某些解题方法不够熟悉，导致在选择策略时感到迷茫；二是不同类型的问题需要不同的解题方法，学生难以根据题目的特点灵活选择合适的策略；三是学生在解题时存在步骤混乱现象，不能按照合理的思路解题，导致其选择解题策略时也变得混乱.

例2如图1，已知数轴上有A，B两点，点A表示的数为-8，且AB=20.若点B在点A的右侧，点P以每秒4个单位的速度从点A出发向右匀速运动.

（1）若点Q同时以每秒2个单位的速度从点B出发向左匀速运动，经过多少秒后，点P与点Q相距1个单位？

（2）若点Q同时以每秒2个单位的速度从点B出发向右匀速运动，经过多少秒后，在点P，B，Q三点中，有一点是另外两个点连接所成线段的中点？

错误解答：（1）（20-1）÷（4+2）=19/6，即经过19/6秒后，点P与点Q相距1个单位.

（2）第一种情况：当B为中点时，8÷4=2，12+2×2=16，从而可知2秒时点Q表示的数为16.因为B为中点，所以（12×2-16）÷（2+4）=4/3，即经过4/3秒，点B为线段PQ的中点；第二种情况：当P为中点时，（12×2-16）÷（4-2）=4，即经过4秒，点P为线段BQ的中点；第三种情况：当Q为中点时，（12×2-12+8）÷（4-2）=10，即经过10秒，点Q为线段PB的中点.

在问题解答过程中，学生只考虑了数轴上动点的某些位置关系，导致问题（1）解答不全面；学生在解题过程中没有充分利用数形结合思想，导致在问题（2）的解答步骤混乱，实际上是学生对解题方法不熟悉，从而导致最后答案错误.

1.3逻辑推理欠缺

在初中数学解题中，学生在数学推理时可能存在思维缺陷，难以进行合理的逻辑推理.究其原因，一是学生在逻辑推理方面较为薄弱，难以理解问题之间的逻辑关系，导致在推理的过程中出现错误；二是学生在分析问题、抓住关键信息上有困难，导致无法正确推理；三是学生不熟悉推理模式与逻辑思维，缺乏有效练习，导致在解决问题时感到困难.

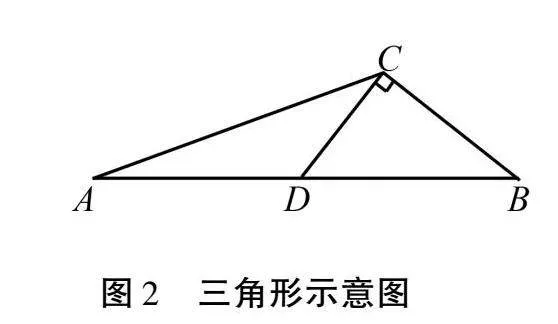
例3如图2，在△ABC中，∠ACB=120°，BC=4，D为AB中点，DC⊥BC，△ABC的面积是多少？

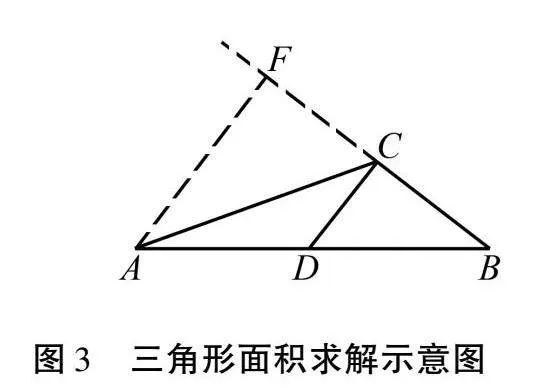
错误解答：如图3，作BC的垂线，交BC的延长线于点F.因为S△ABC=1/2×BC×AF=2AF，但是线段AF的长度无法求出.

在解决本题时，学生因添加辅助线不合理而导致求解过程停滞，实际上就是学生的逻辑思维和几何推理能力有所欠缺.

2解题策略

采用问题解析式解题策略解决问题时，首先要全面理解问题，对问题分析、梳理，然后根据已有的数学知识和解题策略，寻找合适的解题方法和策略解决问题.问题解析式解题的一般步骤分为四步.

第一步：仔细阅读问题，理解问题中的概念［1］.学生应该仔细阅读问题，确保对问题的要求和条件有一个清晰的理解，这样有助于选择合适的解题方法和策略.在阅读问题时，可以通过圈、点、勾、画将问题中的关键信息进行标注和梳理，从而防止遗漏并且确保对问题的内容有全面的了解.

第二步：根据问题的特点，选择适当的数学原理、定理和方法.学生可以根据问题的要求，使用流程图或图表将问题进行可视化处理，使其直观地呈现出来.然后根据所学数学知识与方法，先在草稿纸上把大致思路与步骤进行梳理.最后将已知信息和未知数用数学符号表示，建立适当的数学模型.

第三步：利用已选择的解题方法对问题进行具体的推导和计算.根据建立的数学模型，分解和理清思路，理清每个步骤之间的逻辑关系，然后按照步骤的顺序与先后进行运算.

第四步：在问题解决后，要对其检验和反思.在完成问题解答后，学生需验算或通过逆推检验计算结果，防止因粗心造成解题错误.在完成解题过程后，要回顾解题过程，思考解题中使用的方法和技巧，并且总结经验教训，以便更好地解决类似问题.

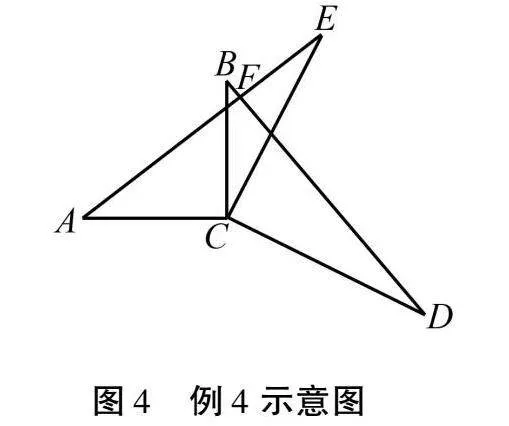
例4如图4，AC⊥BC，DC⊥EC，AC=BC，DC=EC，AE与BD交于点F．

（1）求证：AE=BD；

（2）求∠AFD的度数．

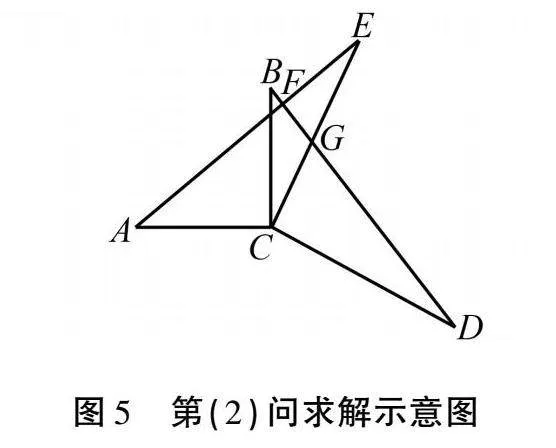
第一步：阅读题目，标注条件.通过观察图4可以发现，已知条件全部集中在两个三角形中，由此可猜测利用△ACE≌△BCD即可解决问题（1）；通过问题（1）可得∠E=∠D，欲求∠AFD的度数，通过观察图5可发现条件都与△EFG和△DCG有关，猜测通过角的等量代换求解问题（2）.

第二步：确定题目类型，选择解题策略.本题是一道与三角形有关的综合题，主要运用全等三角形的性质和判定及角的等量代换解决问题.

第三步：逻辑推理，分步骤计算.

（1）因为AC⊥BC，DC⊥EC，所以∠ACB=∠ECD=90°，所以∠ACB+∠BCE=∠ECD+∠BCE，所以∠ACE=∠BCD.在△ACE和△BCD中，因为AC=BC，∠ACE=∠BCD，DC=EC，所以△ACE≌△BCD，所以AE=BD.

（2）如图5所示，设BD与CE的交点为G.

因为△ACE≌△BCD，所以∠E=∠D.因为∠EFG+∠FGE+∠E=180°，∠GCD+∠CGD+∠D=180°，且∠FGE=∠CGD， 所以∠EFG=∠GCD=90°，所以∠AFD=90°.

第四步：检验答案，反思过程.学生反思有关几何图形的性质，可将类似的问题整理到一起，从而实现量变到质变的转变.

3教学策略

初中数学解题能力与教学策略之间存在密切的关系，教学策略的选择和实施直接影响学生解题能力.为了提高学生解题能力，教师可以根据学生的认知水平与需求改进教学策略.

3.1注重基础知识与基本概念的教学

解题能力的培养需要建立坚实的数学基础.学生应全面掌握数学概念、定理和公式，加强练习和巩固，提高运算和推理能力.教师需帮助学生理解问题背后的概念与原理，而不仅仅是机械地去读题.

3.2加强解题思路与解题方法的教学

在初中数学教学中，教师应该重视数学解题方法.分步解题法是培养学生解题思维和方法的有效途径.教师可帮助学生将复杂问题分解为若干个简单的子问题，通过解决子问题逐步完成解题.通过分步解题，学生能够更好地理清思路，降低解题难度.

3.3加强逻辑思维与分析推理能力的培养

在初中数学教学中，教师需将数学知识与实际问题相结合，通过数学建模等方式培养学生解决问题的能力.在解题教学中，教师还要培养学生在面对复杂问题时

应具备的解决能力和创新能力，包括分析问题的能力、合理推导和计算能力，以及解题过程的系统性和逻辑性.

3.4注重多元评价与及时反馈的落实

在初中数学教学中，教师应及时反馈学生学习情况，帮助其发现错误，改进解题方法.教师可对学生进行个体化反馈，了解他们的弱点，从而针对个体差异提出有针对性的建议，以满足学生的学习需求.

4结束语

数学学习离不开解题，解题离不开经验，经验由错题积累而来，所以错题是学生查缺补漏的优质资源，师生都应该重视错题的成因以及解决策略.在初中数学教学中，教师应该以学生为中心，有效引导学生理解错题的原因，从而使学生更好地理解数学，提高学生运用数学知识分析问题和解决问题的能力.

参考文献：［1］ 王徽.探索初中数学课堂创新教学策略［J］.中学课程辅导，2024（4）：87-89.

［责任编辑：李璟］