极限思维在初中物理解题中的应用

摘要：极限思维在教育实践中引起了越来越多的关注和探讨.文章深入探讨了极限思维在初中物理解题中的重要性，通过分析学生在物理学习中常遇到的问题，结合极限思维理论基础，提出了引导学生运用极限思维解决物理难题的方法和策略.

关键词：极限思维；初中物理；解题能力

中图分类号：G632文献标识码：A文章编号：1008-0333（2024）26-0088-03

在学习初中物理时，学生往往面对各种复杂的问题和挑战，要深入思考和灵活运用知识.极限思维作为一种探索问题本质、突破固有思维定式的方法，对于解决物理难题具有重要意义.

1限定条件下的极限思维

在解决物理问题时，学生经常会遇到一些限定条件，这些条件对问题的解答有着至关重要的影响.限定条件下的极限值一般在临界值处，临界值是问题中某个条件达到极限的点，超过这个点，问题的性质或结果会发生显著变化.因此，通过分析题目中所给条件的临界值，学生可以界定所求变量的取值范围，从而根据问题求出答案［1］.

例如，在考虑一个电路中的电阻变化时，学生可以通过分析电路的布局、元件的特性和电源的电压等条件，找出电路中电流的临界值.当电路中的某个电阻值减小到一定程度时，可能会导致电路中的电流达到最大值，超过这个值，电路可能会发生损坏.通过界定电阻的取值范围，学生可以利用极限思维求出电路中的最大安全电流或最小电阻值等问题的答案.在解决这类问题时，学生通常需要先理解题目中所给的限定条件，然后找出这些条件中的临界值.接着，学生根据临界值将所求变量的取值范围进行界定.最后，学生利用数学方法或物理原理求解问题，得到答案.

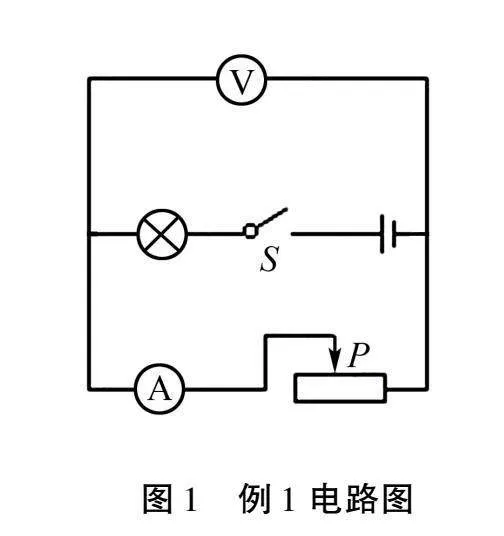
例1小明连接了一个电路，如图1所示，其中电源的电压为18 V，电流表的量程为“0～0.6 A”，电压表的量程为“0～15 V”，规格为“100 Ω，1 A”的滑动变阻器与标有“6 V，3 W”字样的灯泡串联在一起.假设灯丝电阻恒定不变，下列说法正确的是（）.

A.电路安全前提下可通过的最大电流为0.5 A

B.电压表的测量区间为3～6 V

C.灯泡最小的电功率为0.75 W

D.若保证电路安全，滑动变阻器阻值允许的可变区间是24～100 Ω

分析限定条件下的极限思维，需要考虑多重条件，例如，电流表取极值时，应保证最大电流不超过量程，并且整个电路正常运行；电压表取极值时，应综合考虑所测电压器件在整个电路中的分压极值，保证电路正常运行.根据欧姆定律和功率公式，可以通过计算灯泡的电阻和消耗的最小电功率来确定电路中的最小电流值，从而确保电路正常运行.当滑动变阻器两端的电压达到最小值时，电路中的电流达到最大值，可以根据此时的电流值计算出滑动变阻器接入电路的最小阻值范围［2］.

解析由P=UI可知，灯泡的额定电流IL=PLUL=3 W6 V=0.5 A，根据灯泡的额定电流、电流表的量程以及滑动变阻器的规格可知，电路允许通过的最大电流I大=IL=0.5 A，故A正确；灯泡两端的最大电压为6 V，根据串联电路的电压特点可知，滑动变阻器两端的最小电压UR=U-UL=18 V-6 V=

12 V，由于电压表量程为“0～15 V”，所以电压表的示数最大为15 V，则电压表示数的变化范围是

12～15 V，故B错误；由于滑动变阻器两端的最大电压为15 V，根据串联电路的电压特点可知，灯泡两端的最小电压UL=U－UR=18 V-15 V=3 V，由P=U2R可知，灯泡的电阻RL=（UL）2PL=（6 V）23 W=12 Ω，此时电路中的最小电流I小=IL小=ULRL=3 V12 Ω=0.25 A，灯泡消耗的最小电功率PL小=UL小IL小=3 V×0.25 A=0.75 W，故C正确；滑动变阻器接入电路中的最大阻值R大=UR大I小=15 V0.25 A=60 Ω，滑动变阻器接入电路的最小电阻R小=URI太=12 V0.5 A=24 Ω ，所以滑动变阻器允许接入电路的阻值范围为24～60 Ω，故D错误.

练习如图2（甲）所示电路中，电源两端的电压恒定，R0、R1电阻恒定，R2为滑动变阻器.某时刻，闭合开关S，同时滑动滑片，改变R2的阻值，两电压表示数与电流表示数变化关系如图2（乙）所示，当滑片处于滑动变阻器的左端时，电流表示数为0.3 A.

（1）求滑动变阻器R2的最大阻值.

（2）若将滑片置于a、b中点，滑动变阻器R2消耗的电功率为0.8 W，求电源电压U以及R0的阻值.

（3）若R2滑片每移动1 cm，其阻值变化1 Ω，设a、b端距离为x cm，写出滑动变阻器消耗的电功率P随x变化的关系式，并由此关系式求出R2消耗电功率的最大值.

分析（1）当变阻器连入电路的电阻最大时，电路的电流最小，由图可知最小电流和R2的示数，由欧姆定律得出R2的最大阻值.（2）当R2接入电路的电阻达到最大时，根据串联电路的性质以及欧姆定律可以计算出R1的阻值；当R2接入电路的电阻减小到5 Ω时，可计算得到电流值；根据电压规律及欧姆定律，可计算得到U和R0.（3）滑片移动x cm时，R2接入电路的电阻为R2=x Ω，由串联电阻的规律及欧姆定律，可计算出电路的电流表达式，根据电功率公式，由数学知识求出变阻器消耗电功率的最大值.

2隐含条件下的极限思维

在解决物理问题时，学生经常会遇到一些隐含条件，这些条件并没有直接给出，而是隐藏在问题的背景或物理规律之中.要准确找出这些隐含条件，学生需要对问题进行深入分析，这往往涉及对物理知识的深入理解和灵活运用.隐含条件下求极值是极限思维的进阶应用，它要求学生在理解问题的基本条件的基础上，进一步挖掘问题背后的物理规律和逻辑关系，从而找到不易察觉的限定条件［3］.

在找到这些隐含的限定条件后，学生就可以根据这些条件进行极值的求解.例如，对一个装水的容器，当容器受到外力作用时，容器底部所承受的压强会发生变化.在这种情况下，学生可以通过分析容器的形状、尺寸以及外力的大小和方向，找出容器底部压强的临界值.通过界定外力的取值范围，学生可以利用极限思维求出容器底部所能承受的最大压强或最小安全压强等问题的答案.在解决这类问题时，学生通常需要先建立物理模型，然后分析其中的变量和参数，找出可能的临界点，这些临界点往往是极值出现的地方.

隐含条件下求极值是极限思维的一种高级形式，它要求学生不仅要有扎实的物理知识基础，还要有敏锐的洞察力和严谨的逻辑思维能力.

例2两个装有水的玻璃圆筒如图3所示方式放置，已知大玻璃圆筒的半径为小玻璃圆筒半径的2倍，圆筒厚度不计，将等体积的两个小球A、B投入小圆筒中，此时两圆筒内的水对各自圆筒底部压强的增量相同.则小球A的密度的最大值为（）.

A.4×103 kg/m3 B.5×103 kg/m3C.6×103 kg/m3D.7×103 kg/m3

分析已知两圆筒内的水对各自底部压强的增量相同，可根据F=pS分析压力的增加量，根据阿基米德原理可以分别得出深度的变化量.通过极限思想，要想小球A的密度的最大，那么B球的密度应为最小，此时可以推断出，B球的密度应该等于水的密度.

解析根据题意可知，两容器内的水对各自容器底部压强的增加量相等，大容器的底面积是小容器的4倍，根据F=pS可知，大容器和小容器底部所受水的压力的增加量关系为△F1=4△F2.设两球的体积均为V，由图可得A、B两个小球完全浸没在水中，因此小球排开水的体积为V排1=2 V，小容器中水面上升的高度△h1=V排S小=2VS小，则小容器中的水对其底部压强的增加量为△p小=ρ水g△h1=ρ水g×2 VS小；由于小容器漂浮在圆柱形大容器中，所以A、B投入小容器后，水对大容器底部压力的增加量为△F=GA+GB=ρAgV+ρBgV，则大容器底部压强的增加量为△p大=△FS大=ρAgV+ρBgVS大；由题意可知△p大=△p小，所以，ρAgV+ρBgVS大=ρ水g×2VS小，由于B球是需要浸没在水中的，所以B球的最小密度为ρB最小=ρ水，因此，小球A的最大密度ρA最大=8ρ水－ρB最小=8ρ水－ρ水=7ρ水=7×103 kg/m3，故A、B、C错误，D正确.本题关键是根据题目要求，用极限思维得出A、B球要浸没在水中的条件是球的密度必须大于或等于水的密度.

3结束语

极限思维不仅能帮助学生更好地理解物理知识，还能激发他们的求知欲和探索精神.通过深入探讨极限思维在初中物理解题中的应用，教师可以引导学生充分发挥创造力，提高问题解决能力.

参考文献：［1］ 施燕莹.极限思维法在初中物理解题中的运用［J］.数理化解题研究，2022（2）：88-90.

［2］张晓芳.极限思维法在初中物理解题中的妙用［J］.试题与研究，2019（30）：144.

［3］袁柏林.用“极限法”巧解初中物理问题［J］.理科考试研究，2018，25（10）：33-38.

［责任编辑：李璟］