以不变应万变的二次函数

摘要：二次函数是初中数学“数与代数”部分的重要内容.二次函数的性质是解决数学问题的基本工具，在不同领域问题解决中具有广泛应用.从存在性问题、动点变化到与不同图形的碰撞融合，二次函数在解题中展现着自己千变万化的魅力.聚焦二次函数与不同图形交叉融合的综合题模型，剖析二次函数综合题的求解思路，提高学生分析问题和解决问题的能力.

关键词：初中数学；二次函数；圆；平行四边形；矩形

中图分类号：G632文献标识码：A文章编号：1008-0333（2024）26-0033-03

二次函数是初中数学的重要内容，是中考数学的热点问题，倍受命题者的青睐.在历年中考数学试题中，它总是以意想不到的方式考查学生对二次函数有关知识的掌握情况.笔者以二次函数与不同几何图形融合的综合问题为研究对象，探究不同类型问题的解题思路，启发学生灵活运用二次函数知识分析问题和解决问题，以不变应万变.

1二次函数与圆的综合性问题

在圆与二次函数图象融合的综合性问题中，教师可启发学生根据图形结构特征，充分利用圆的有关几何性质解决问题［1］.

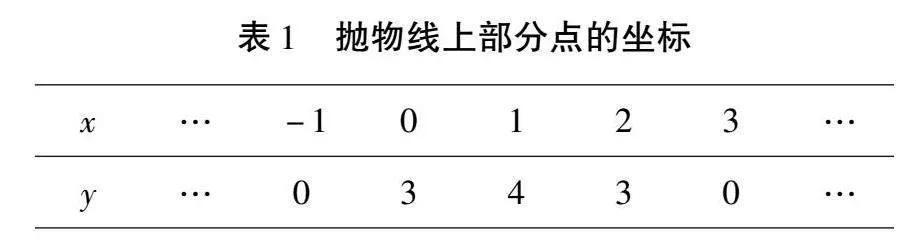
例1如图1，在平面直角坐标系xOy中，抛物线y=ax2+bx+c与x轴分别相交于A、B两点，与y轴相交于点C，下表给出了这条抛物线上部分点（x，y）的坐标值.

（1）求抛物线的解析式及顶点M的坐标；

（2）PQ是抛物线对称轴上长为1的一条动线段（点P在点Q上方），求AQ+QP+PC的最小值；

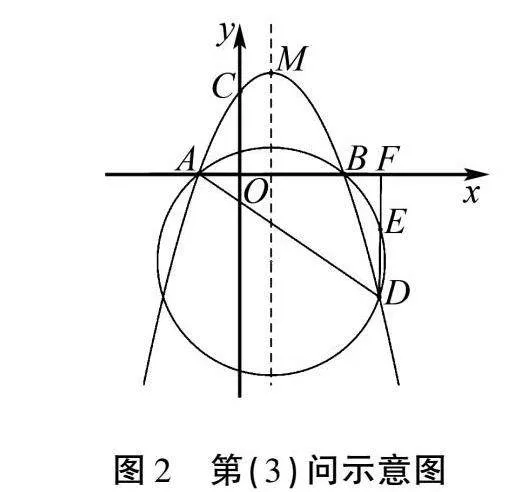
（3）如图2，点D是第四象限内抛物线上一动点，过点D作DF⊥x轴，垂足为F，△ABD的外接圆与DF相交于点E，线段EF的长是否为定值？如果是，请求出这个定值；如果不是，请说明理由.

解析（1）根据表1给出的抛物线上部分点的坐标，利用待定系数法即可求出解抛物线解析式，这也是求解函数表达式常用方法之一.对于抛物线的顶点坐标，一方面可利用配方法求解，另一方面可直接利用顶点坐标公式求解.由表1可知，A（-1，0），B（3，0），C（0，3）.设抛物线解析式为y=a（x+1）（x-3），将C（0，3）代入，得3=a（0+1）（0-3），解得a=-1，所以y=-（x+1）（x-3）=-x2+2x+3=-（x-1）2+4.由此可知，抛物线的解析式为y=-x2+2x+3，其顶点坐标为M（1，4）.

（2）点P和点Q的位置不确定，点A和C点的位置是确定的，所以需要改变某些点的位置，尝试寻找三点共线的位置，然后利用“两点之间，线段最短”解决问题.显然，需将三条线段之和转化为两条线段之和，减少不必要的线段.由于线段QP的长度确定，所以可尝试使得A，Q，C存在三点共线的情形.结合图形易发现，将C点进行平移可出现A，Q，C三点共线的情形，故需添加辅助线.

如图3，将C点沿y轴向下平移1个单位得到C′0，2，连接BC′交抛物线的对称轴x=1于点Q′，过点C作CP′∥BC′，交对称轴于点P′，连接AQ′.因为关于直线x=1对称，所以AQ′=BQ′.因为CP′//BC′，P′Q′∥CC′，所以四边形CC′Q′P′是平行四边形，所以CP′=CQ′，Q′P′=CC′=1.在Rt△BOC′中，BC′=OC′2+OB2=22+32=13.由于A、B点在二次函数图象上且处于对称轴的两边，由二次函数性质可知AQ′+Q′P′+P′C=BQ′+C′Q′+Q′P′=BC′+Q′P′=13+1.

（3）如图4，连接BE，因为点D在二次函数上，所以可设D（t，-t2+2t+3），且t＞3.

因为EF⊥x轴，所以DF=--t2+2t+3=t2-2t-3.根据所设点D的坐标可确定点Ft，0，所以BF=OF-OB=t-3，AF=AO+OF=t--1=t+1.因为四边形ABED是圆内接四边形，所以∠DAF+∠BED=180°，又因为∠BED+∠BEF=180°，所以∠DAF=∠BEF.因为∠AFD=∠EFB=90°，所以△AFD∽△EFB，所以EFBF=AFDF，即 EFt-3=t+1t2-2t-3，所以EF=t+1t-3t2-2t-3=t2-2t+3t2-2t+3=1，所以线段EF的长为定值1.

点评本题是一道二次函数与圆的综合性问题，对于问题（2），其本质就是“将军饮马”几何模型，但并不能直接套用模型，需要学生结合轴对称和平移等图形变换才能解决问题.在解题过程中，找到AQ+QP+PC最小时点P和点Q的位置也是解题关键.对于问题（3），利用圆内接四边形的性质寻找相似三角形，可为问题解决提供简洁清晰的思路.在解题教学中，教师一定要注意引导学生对所学知识融会贯通，使学生明白“形”中有“数”，“数”中有“形”，为数形结合思想运用奠定基础.

2二次函数与平行四边形的综合性问题

例2如图5，已知抛物线y=ax2+bx+4（a≠0）与x轴分别相交于A（1，0）和B两点，于y轴相交于点C，对称轴为x=2.5.

（1）求抛物线的解析式；

（2）如图5，若点P是线段BC上的一个动点（不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，连接OQ，当线段PQ长度最大时，判断四边形OCPQ的形状并说明理由.

（3）如图6，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且∠DQE=2∠ODQ.在y轴上是否存在点F，使△BEF为等腰三角形？若存在，求F的坐标；若不存在，说明理由.

解析（1）因为抛物线y=ax2+bx+4（a≠0）与x轴交于A（1，0），且对称轴为x=2.5，从而可得a+b+4=0，-b2a=52，解得a=1，b=-5.故y=x2-5x+4.

（2）由（1）可求得点B，C坐标.令y=x2-5x+4=0，解得x1=1，x2=4.令x=0，则y=4，所以点B坐标为4，0，点C坐标为0，4.点P是线段BC上的一个动点（不与点B，C重合），设直线BC的表达式为y=kx+t，则t=4，4k+t=0，解得k=-1，t=4.故直线BC的表达式为y=-x+4.设点P坐标为x，-x+4，则点Q坐标为x，x2-5x+4，从而可得PQ=-x+4-x2-5x+4=-x2+4x，故PQ的长度与二次函数有关.由二次函数性质可知，当x=-42×-1=2时，线段PQ的长度最大，最大值为PQmax=-22+4×2=4，所以点P坐标为2，2，点Q坐标为2，-2，此时OC=PQ，由题意可知OC//PQ，故四边形OCPQ为平行四边形.

（3）根据已知条件可直接写出点D坐标为0，2，点Q坐标为2，-2，所以直线DQ的表达式为y=-2x+2.如图7，过点Q作QH⊥x轴于点H，则QH//CO，故∠AQH=∠ODA.

因为∠DQE=2∠ODQ，所以∠HQE=∠HQA，故直线DQ和直线QE关于直线QH对称，可设直线QE的表达式为y=2x+r，将点D（0，2）代入y=2x+r中，得r=-6，所以直线QE的表达式为y=2x-6.与二次函数表达式联立y=x2-5x+4，y=2x-6，解得x=5，y=4.故点E的坐标为（5，4），由题意设点F坐标为（0，m），由点B，E的坐标可写出BE2=（5-4）2+（4-0）2=17，要使△BEF为等腰三角形，则存在三种情况：①BE=BF，即16+m2=17，解得m=±1；②BE=EF，即25+（m-4）2=17，方程无解；③BF=EF，即16+m2=25+（m-4）2，解得m=3.125；所以点F的坐标为（0，1）或（0，-1）或（0，3.125）.

点评问题（1）是常规题目，重在考查学生的基础知识与基本技能.问题（2）中出现四边形，目前学生学习过的规则四边形数量有限，可从已知图形开始尝试证明，题目中的平行线为解题者提供了思路.因为该四边形的一组对边平行，所以可以尝试证明该四边形是正方形、矩形、菱形、平行四边形或梯形.因正方形、矩形、菱形是特殊的平行四边形且图象的大致形状不满足梯形，所以首先考虑该四边形是平行四边形.平行四边形的证明方法多样，含有“一组对边平行”的证明方法有两种，即“两组对边分别平行”或“一组对边平行且相等”.然后利用二次函数性质可以发现这一组平行的对边是相等的，故可证明该四边形为平行四边形.问题（3）中学生需要寻找等腰三角形中三个点的位置，可以先在题目条件中首先求出确定点的位置，然后假设不确定点，通过点坐标表示线段长度，对不同情形进行分类讨论，使用这种解题思路，学生不需要画图辨别，只需要通过不同点的数量关系就可以求解出结果.

3结束语

数形结合思想是解决函数问题的有效工具.它可以帮助学生利用图形结构特征直观解决问题.在解题过程中，使用图形并不意味着它就可以脱离原本的条件关系，函数关系式就是其中的限制条件.在初中数学教学中，教师需帮助学生以不变应万变，抓住问题关键，为问题解决创造便利条件.

参考文献：［1］ 张继华.数形结合解决二次函数问题［J］.中学生数理化（初中版），2023（10）：6-7.

［责任编辑：李璟］