三角形折叠问题的求解策略

摘要：三角形折叠问题主要考查学生的动手能力与直观想象能力，深受中考命题专家的青睐. 解决折叠问题的关键，一是抓住几何图形折叠前后保持不变的量，即对应线段相等，对应角相等；二是抓住几何图形中垂直关系，为问题解决创造条件.基于此，先给首出三角形中常见折叠问题的三个基本模型，然后给出三角形折叠问题的求解策略，最后结合典型的折叠类试题，对三角形折叠问题进行深入探究，以期为初中数学教学提供参考.

关键词：三角形；折叠问题；模型；探究

中图分类号：G632文献标识码：A文章编号：1008-0333（2024）26-0012-03

《义务教育数学课程标准（2022年版）》对学生的动作操作能力提出了更高的要求，最近几年的中考试题也频繁考查学生的动手操作能力.为此，笔者结合典型的折叠类试题，探究三角形折叠问题的求解策略，供读者参考.

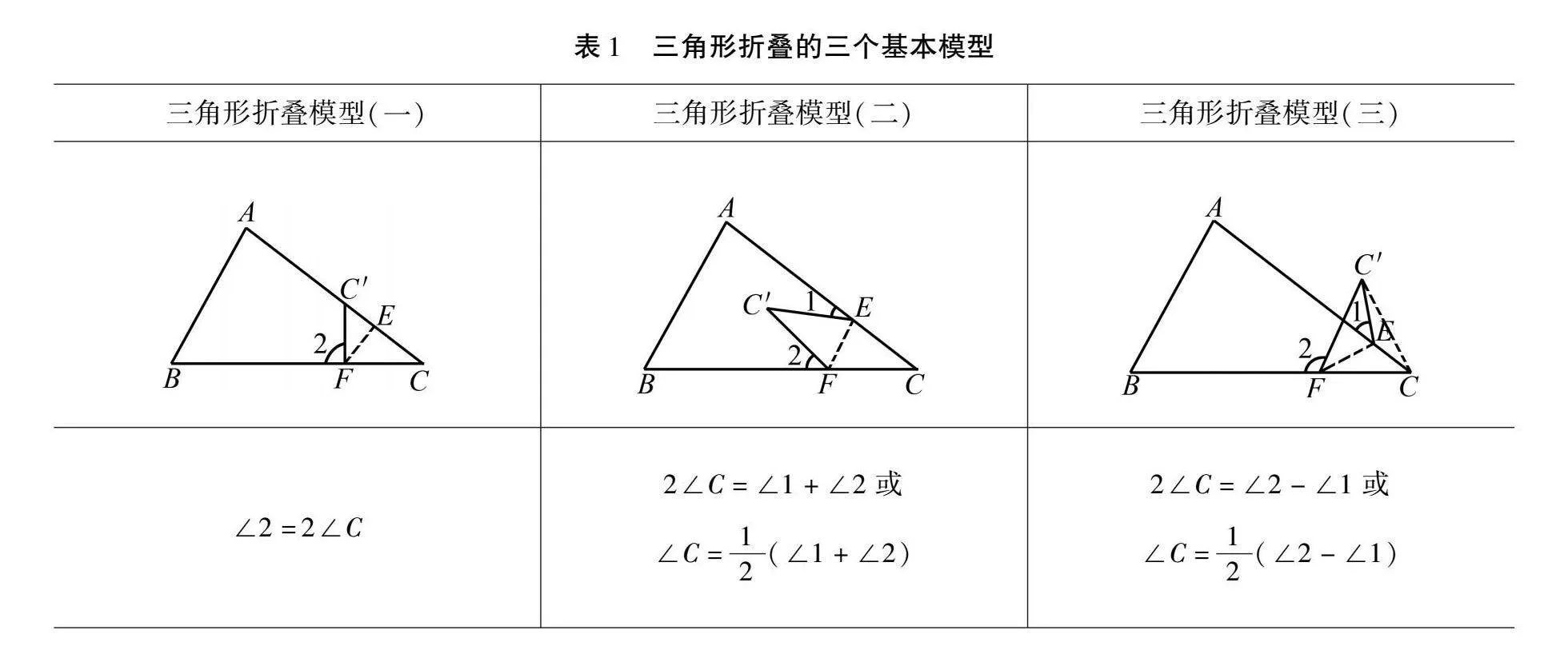
1三角形折叠的三个基本模型

在初中数学学习中，三角形折叠是常见的几何问题，其形式灵活多样.不论几何图形如何变化，三角形折叠的本质是图形的轴对称变换，其有三个基本模型.如表1所示，将△ABC沿直线EF折叠，点C落在C′处，即△CEF与△C′EF关于直线EF对称，易知△CEF≌△C′EF.根据不同图形的结构特征，利用全等三角形的性质、三角形的内角和定理及三角形外角的性质易求得∠1，∠2，∠C之间的数量关系，这是解决三角形折叠问题的基本依据.

2三角形折叠问题的求解策略

在初中数学试题中，三角形折叠问题主要以填空题及综合题的形式出现，一般属于多解型问题，其难度系数较大．在解决三角形折叠问题时，要注意折叠前后“对应线段相等，对应角相等，对应点的连线被折痕垂直平分”等结论的运用. 在多解题型中，准确画出折叠后的图形是解题的关键［1］．解题时往往需要用到三角形的有关性质、判定定理、推论及其他相关的几何知识．具体解题步骤如下：第一步，运用折叠图形的性质找出相等的线段或角；第二步，在图形中找到一个直角三角形.通常选择不以折痕为边的直角三角形，然后设图形中某一线段的长为x，将此直角三角形的未知边长用含有x的代数式表示出来；第三步，利用勾股定理列方程求出x的值；第四步，通过相关计算解决问题.

3应用举例

例1如图1，点M，N分别是长方形ABCD的边AB和BC上的点，沿MN折叠长方形ABCD，点B落在点B′处，若∠MNB′与∠CNB′两个角之差的绝对值为45°，求∠BNM的度数．甲的结论是∠BNM=45°，乙的结论是∠BNM=60°．下列判断正确的是（）.

A．甲的结论正确B．乙的结论正确

C．甲、乙的结论合在一起才正确D．甲、乙的结论合在一起也不正确

解析由折叠的性质可知∠MNB′=∠BNM.

①当∠MNB′与∠CNB′两个角之差为45°，即∠MNB′=∠CNB′+45°时，∠CNB′=∠MNB′-45°=∠BNM-45°.因为∠MNB′+∠MNB+∠CNB′=180°，所以∠BNM+∠BNM+∠BNM-45°=180°，解得∠BNM=75°.

②当∠CNB′与∠MNB′两个角之差为45°，即∠MNB′=∠CNB′-45°时，∠CNB′=∠MNB′+45°=∠BNM+45°.因为∠MNB′+∠MNB+∠CNB′=180°，所以∠BNM+∠BNM+∠BNM+45°=180°，解得∠BNM=45°.

综上所述，∠BNM=75°或45°，故选D．

点评本题主要考查折叠的性质、

三角形内角和定理、一元一次方程等知识. 由折叠的性质可知∠MNB′=∠BNM.根据图形结构特征，需分两种情况讨论求解，一是∠MNB′与∠CNB′两个角之差为45°；二是∠CNB′与∠MNB′两个角之差为45°. 由此可以看出，掌握折叠的性质，利用三角形内角和定理建立方程是解题的关键．

例2如图2，△ABC中，点D是BC上一点，将△ABD沿着AD翻折，得到△ADE，AE交BC于点F．若AE⊥BC，点D到AB的距离等于（）.

A．DFB．DBC．DCD．CF

解析由折叠可知∠BAD=∠EAD.因为DF⊥AE，所以点D到AB的距离等于DF，故选A．

点评本题主要考查角平分线的性质、折叠的性质、点到直线的距离等知识，掌握角平分线的性质是解题的关键．

例3如图3，小明从一张三角形纸片ABC的AC边上选取一点N，将纸片沿着BN对折一次使得点A落在A′处后，再将纸片沿着BA′对折一次，使得点C落在BN上的C′处，已知∠CMB=68°，∠A=18°，则原三角形的∠C的度数为（）.

A．87°B．84°C．75°D．72°

解析由折叠的性质可知∠ABN=∠A′BN=∠A′BC，所以∠ABC=3∠A′BC.因为∠A′BC+∠C+∠CMB=180°，∠A+3∠A′BC+∠C=180°，∠CMB＝68°，∠A＝18°，从而可得∠A′BC+∠C+68°=180°，18°+3∠A′BC+∠C=180°，解得∠C=87°，故选A.

点评本题主要考查折叠的性质、三角形内角和定理、二元一次方程组等知识，掌握折叠的性质是解题的关键．根据折叠的性质可知∠ABN=∠A′BN=∠A′BC，根据三角形内角和定理可得∠A′BC+∠C+∠CMB=180°，∠A+3∠A′BC+∠C=180°，进而可得∠C的度数．

例4如图4，在直角△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段AN的长为（）.

A．6B．5C．4D．3

解析设AN=x，易知DN=AN=x，则BN=9-x．因为D是BC的中点，所以BD=3．在Rt△BDN中，由勾股定理得ND2=NB2+BD2，即x2=（9-x）2+32，解得x=5，所以AN=5，故选B．

点评本题主要考查折叠的性质和勾股定理的应用. 由折叠的性质易得DN=AN=x，BN=9-x.在Rt△BDN中利用勾股定理列出关于x的方程，这是解决本题的关键．

例5如图5，在△ABC中，∠B=42°，∠C=68°，点E为线段AB的中点，点F在边AC上，连接EF，沿EF将△AEF折叠得到△PEF．

（1）如图5，当点P落在BC上时，求∠BEP的度数；

（2）如图6，当PF⊥AC时，求∠AEF的度数．

解析（1）由折叠的性质可得AE=EP.因为AE=EB，所以BE=EP，所以∠B=∠BPE=42°.因为∠B+∠BPE+∠BEP=180°，所以∠BEP=180°-∠B-∠BPE=180°-42°-42°=96°.

（2）因为PF⊥AC，所以∠PFA=90°.易得∠AFE=∠PFE，∠AEF=∠PEF，所以∠AFE=∠PFE=45°.在△ABC中，∠A+∠B+∠C=180°，所以∠A=180°-∠B-∠C=180°-42°-68°=70°.在△AEF中，∠AEF+∠A+∠AFE=180°，所以∠AEF=180°-∠A-∠AFE=180°-70°-45°=65°．

点评本题主要考查折叠的性质、等腰三角形的性质、三角形内角和定理等知识，解题的关键是根据折叠的性质得到相等的线段和角，然后利用三角形内角和定理列方程求解.

4结束语

三角形折叠问题对学生的动手操作能力和直观想象能力要求较高，在初中数学教学中，教师需注重培养学生的动手操作能力和直观想象能力.通过教学活动，让学生感受到折纸的乐趣和数学的魅力，激发学生的学习兴趣，提高学生的动手操作能力，从而提高学生的直观想象能力.

参考文献：

［1］ 畅英英.初中数学教学中有关折叠问题的解题研究［J］.数理化解题研究，2021（29）：28-29.

［责任编辑：李璟］