探究向心力大小的实验创新设计

关键词：高中物理；核心素养；向心力；实验创新

中图分类号：G633.7" "文献标识码：B" "文章编号：1009-010X（2023）26-0059-04

一、学情分析

高一年级的学生通过高中物理必修第一、二册的学习，学习了物体做曲线运动的条件、受力与转弯的关系等知识，对力与运动的部分知识和学习方法建立了初步的认识，在物理观念和科学思维方面具备了化曲为直、化繁为简及微元和极限的思想，同时也掌握了科学探究的一般思路，但是对圆周运动的深入认知方面存在不足，表现为对向心力缺乏感性认识，抽象思维能力和逻辑推理能力不是很强。因此，在实验探究方面，如何巧妙设计以培养学生的核心素养是值得研究的问题。本文就探究向心力大小的实验设计进行简要探讨。

二、实验教学目标

（一）课标要求

会用线速度、角速度、周期描述匀速圆周运动；知道匀速圆周运动向心加速度的大小和方向；通过实验，探究并了解匀速圆周运动向心力大小与半径、角速度、质量的关系；能用牛顿第二定律分析匀速圆周运动的向心力；了解生产生活中的离心现象及其产生的原因。

（二）学习目标

物理观念：知道什么是向心力，理解向心力是一种效果力；知道向心力大小与哪些因素有关，并能进行简单的情境分析计算。

科学思维：在探究向心力表达式的过程中，体会控制变量思想在解决问题中的作用。

科学探究：在探究向心力概念的过程中，理解向心力的内涵；在验证向心力表达式的过程中，学会用力和运动的观点分析解决问题。

科学态度与责任：经历从提出问题到解决问题的过程，培养学生的问题意识及思维能力；经历从特殊到一般的研究过程，培养学生分析问题、解决问题的能力；实例、实验紧密联系生活，拉近科学与学生的距离，调动学生学习的积极性，培养学习兴趣。

三、实验探究过程的改进与创新

本节课的实验设计，首先利用自制教具进行实验，对向心力的影响因素进行猜想，然后利用phyphox测量向心力和角速度的关系，最后利用DIS数字化实验系统完成定量探究，得到向心力的定量表达式。实验探究过程按照发现问题、收集证据、互动交流、解释现象的主线，分以下三个层次。

（一）定性猜想——感知向心力大小与哪些因素有关

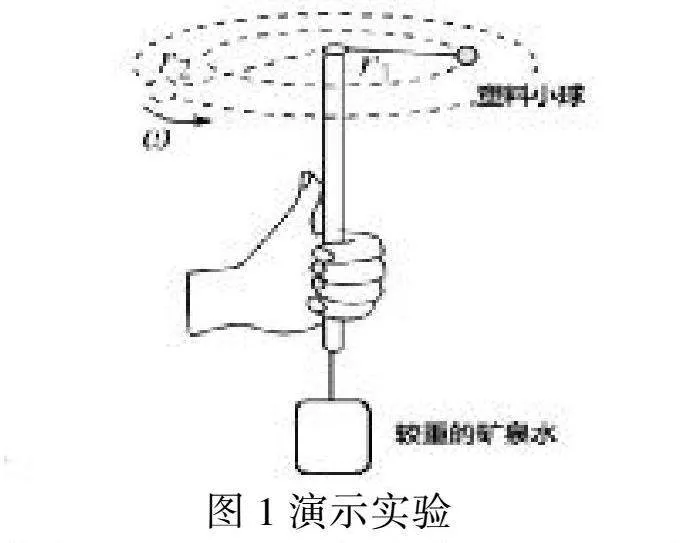
通过观察教师将较轻的塑料小球旋转起来带起较重的矿泉水的演示实验（图1），结合学生利用绳拉较轻的乒乓球和绳拉较重的橡胶球使球做圆周运动的操作，学生猜想向心力的大小可能与物体的质量、半径和角速度有关。

（二）验证猜想——学生分组实验，半定量探究向心力

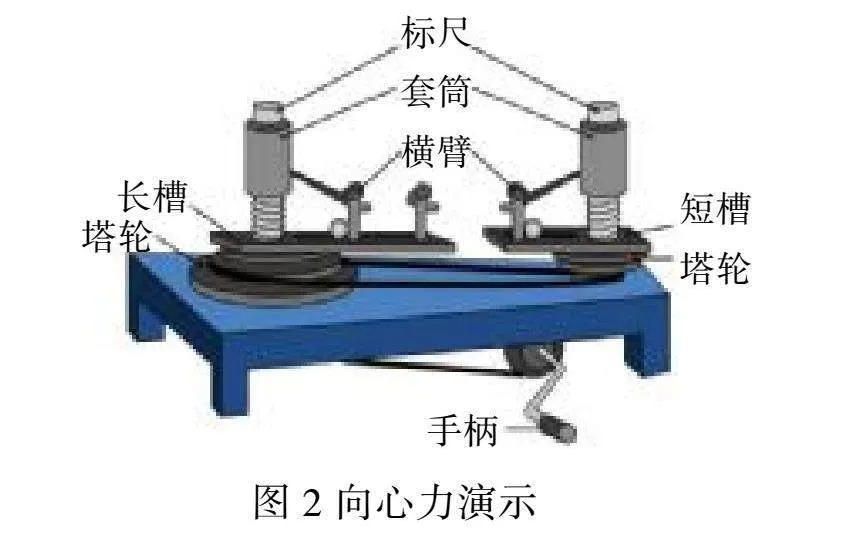
向心力的大小与多个因素有关，需采用控制变量法进行探究。学生利用向心力演示器（图2），进行分组实验，通过分析归纳实验现象，获得证据，初步得出实验结论，并作出解释。

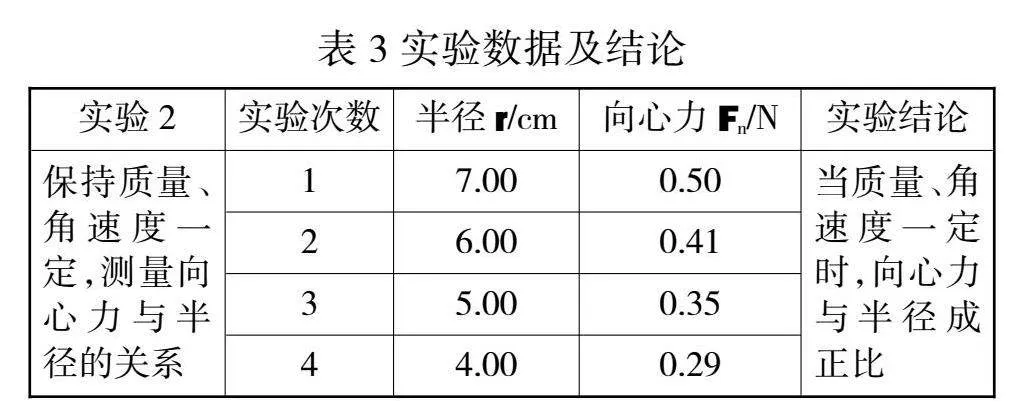
学生分组实验后，得到以下实验规律：（1）当半径、角速度一定时，向心力大小与质量成正比；（2）当质量、加速度一定时，向心力的大小与半径成正比；（3）当质量、半径一定时，向心力的大小与角速度的平方成正比。

学生做第（3）组实验时发现：由于向心力演示器的变速塔轮结构导致观测存在困难，而且角速度只能准确测出一组数据。为了克服这一困难，可把“隐性”的难以定量测量的角速度变成“显性”，便于观察和思考。于是改进实验：把手机固定在水平横梁上，转动手柄让手机做圆周运动，利用手机中的phyphox软件，把不可视的角速度测量转换成可视化测量，测量的数据如表1。

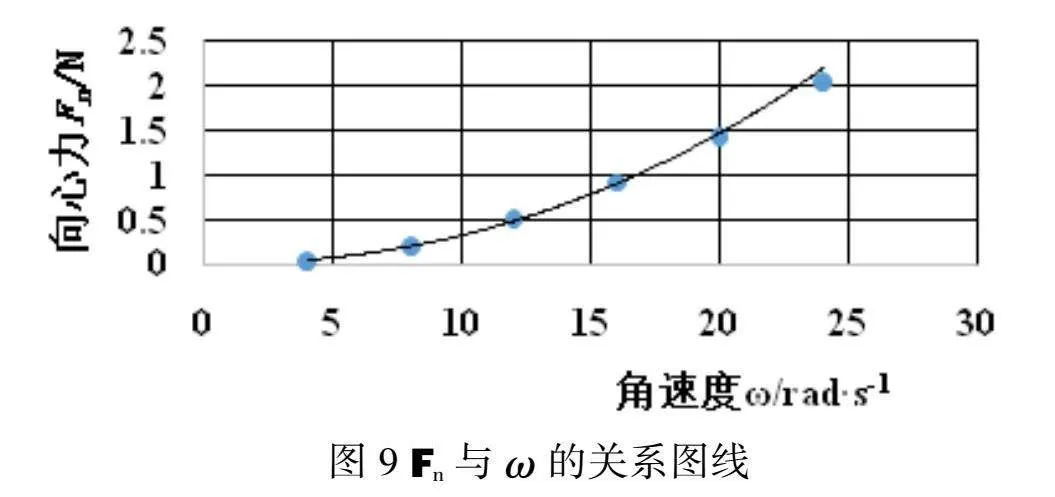
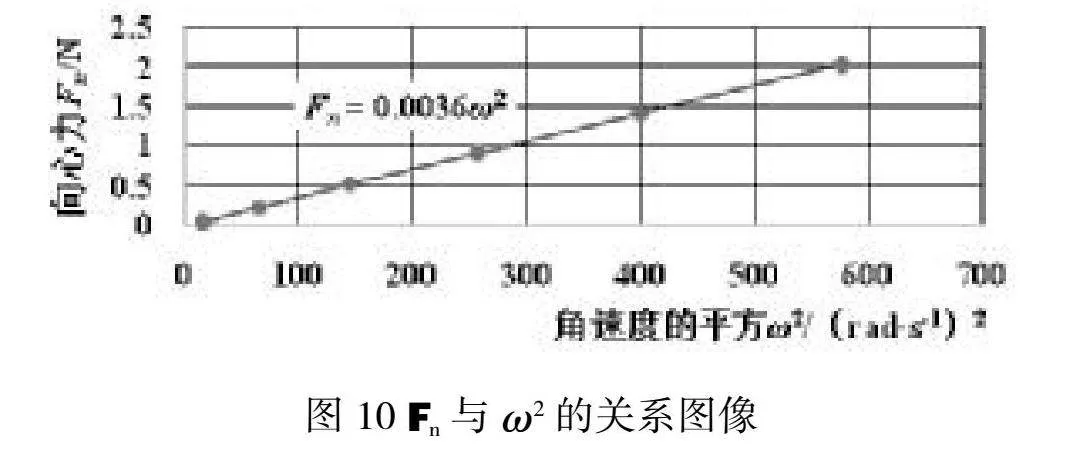
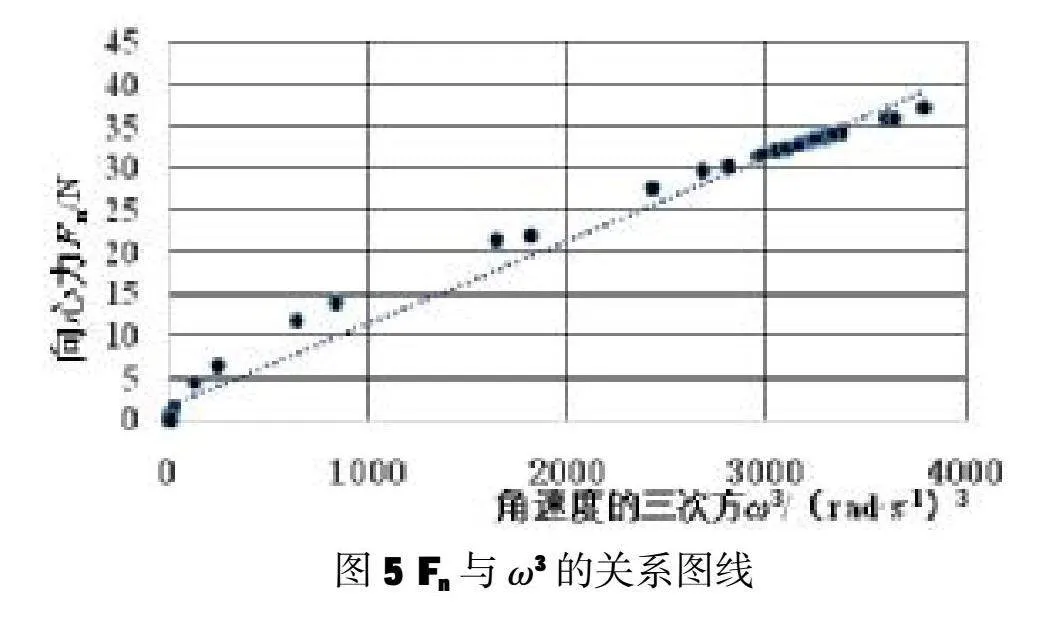
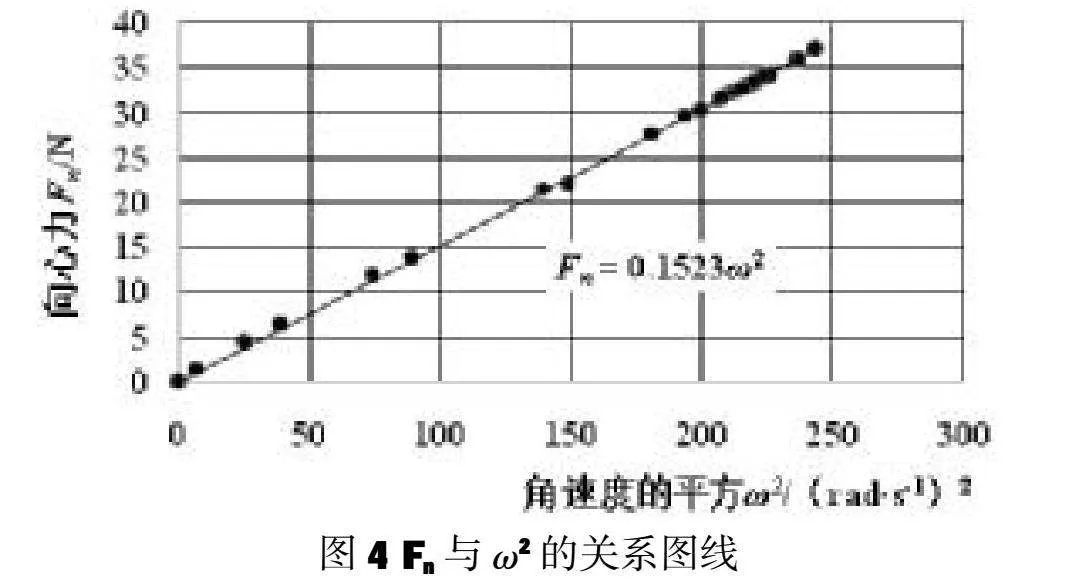
利用Excel作图得到向心力的大小与角速度的关系如图3所示，由图可知两者不是线性关系。学生继续猜想与角速度的平方的关系，作图后可知，向心力的大小与角速度的平方是一条过原点的直线（图4）。为了更加严谨地说明规律，再作一个对比关系图，向心力的大小与角速度的三次方关系（图5）。对比三个图像，可以得出结论：向心力的大小与角速度的平方成正比。

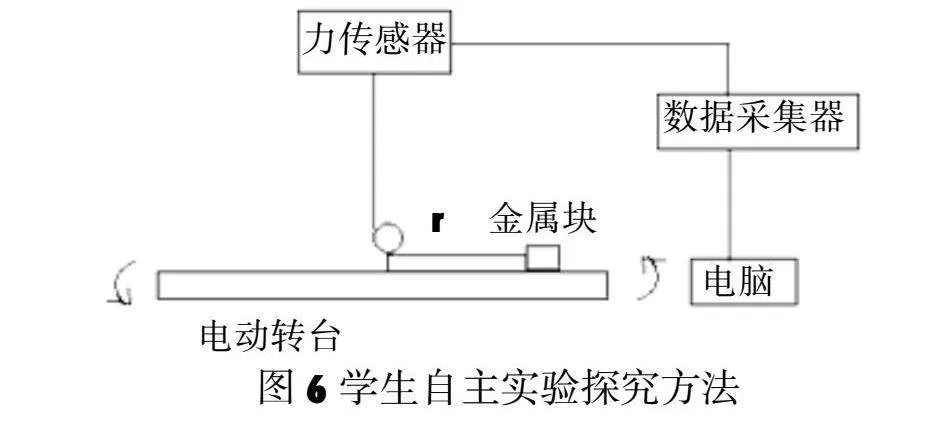
以上方案解决了第（3）组实验出现的问题，但有学生发现塔轮实验还有不足：塔轮的半径是定值，只能根据半径之比研究成比例的特殊数据，无法测量各个物理量的具体数值。因此学生利用电动转台、力传感器、铁架台、电脑等器材完成自主实验探究（图6），测量的实验数据如表2和表3。

与向心力演示器的分组实验相比，采用此实验方案，学生容易测量多组向心力、运动半径和质量的大小。但是由于自制电动转台的转速不能准确测量，导致不能准确测量角速度的大小。要克服测量角速度的困难且使实验数据从特殊到一般，需要更精密的仪器，因此我们设计了第三个层次的实验。

（三）定量探究向心力大小的表达式

利用传感器DIS数字化实验系统完成更进一步的定量探究（图7）。实验中，通过力传感器测出向心力Fn的大小，电机控制器改变角速度ω的大小，水平横梁上的标尺可以测量运动半径。借助DIS数据采集器以及计算机等工具分析Fn与m、r、ω之间的定量关系。

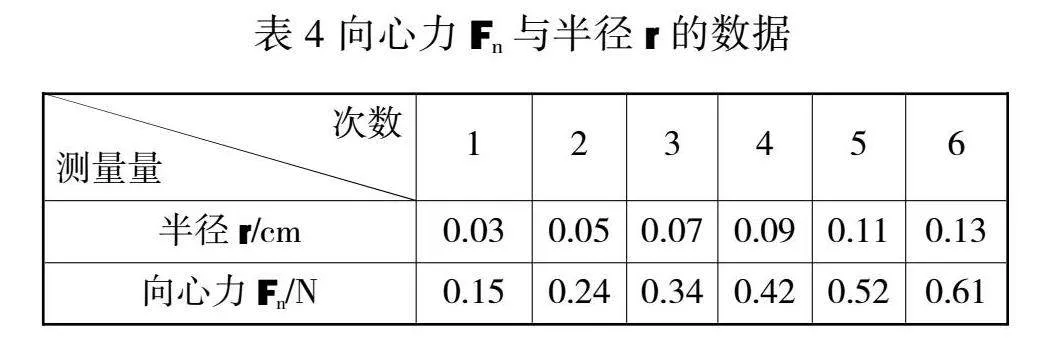
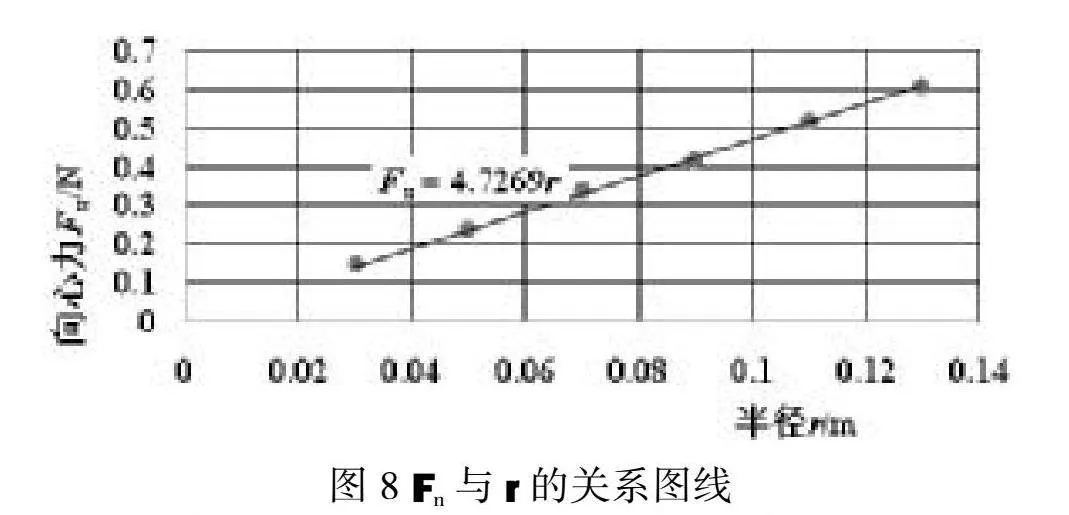
1.当m=0.02kg，ω=15rad/s时，Fn与r的测量数据如表4，拟合图像如图8。

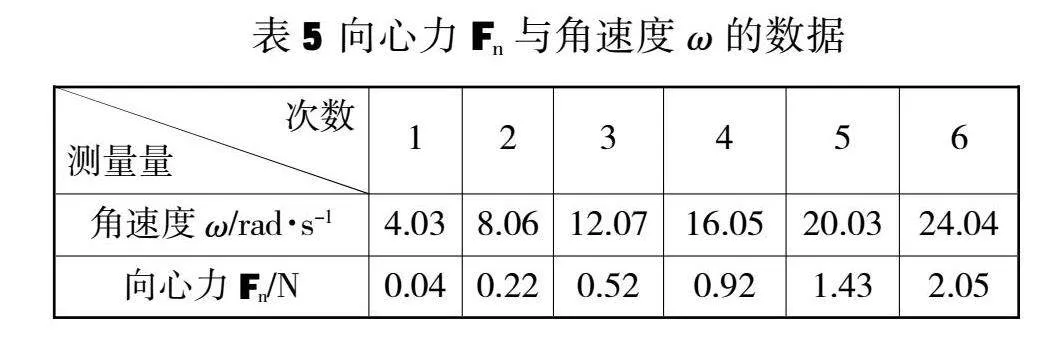
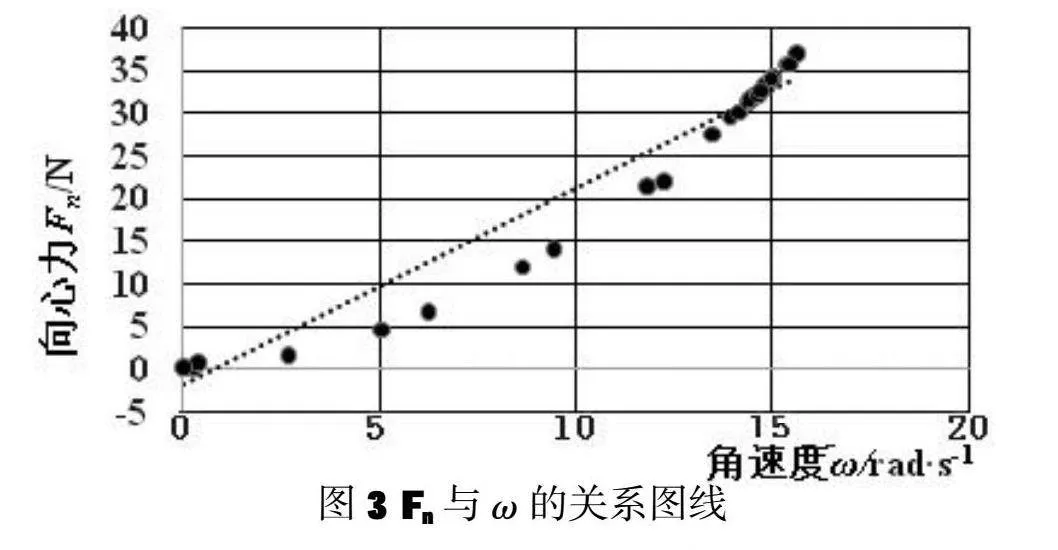
2.当m=0.02kg，r=0.11m时，Fn与ω的测量数据如表5，拟合图像如图9和图10。

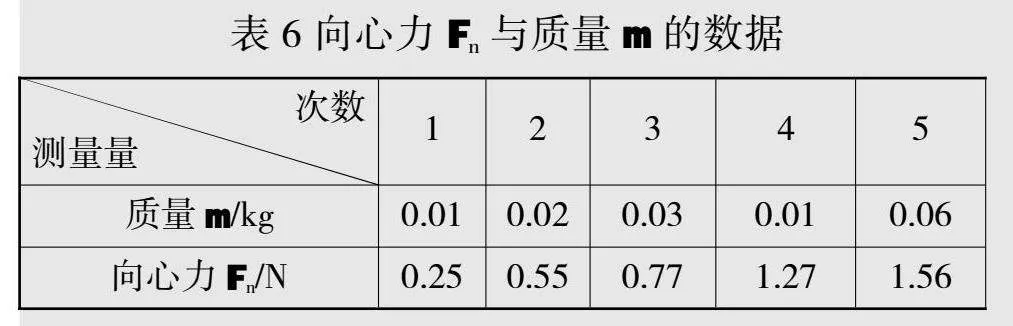
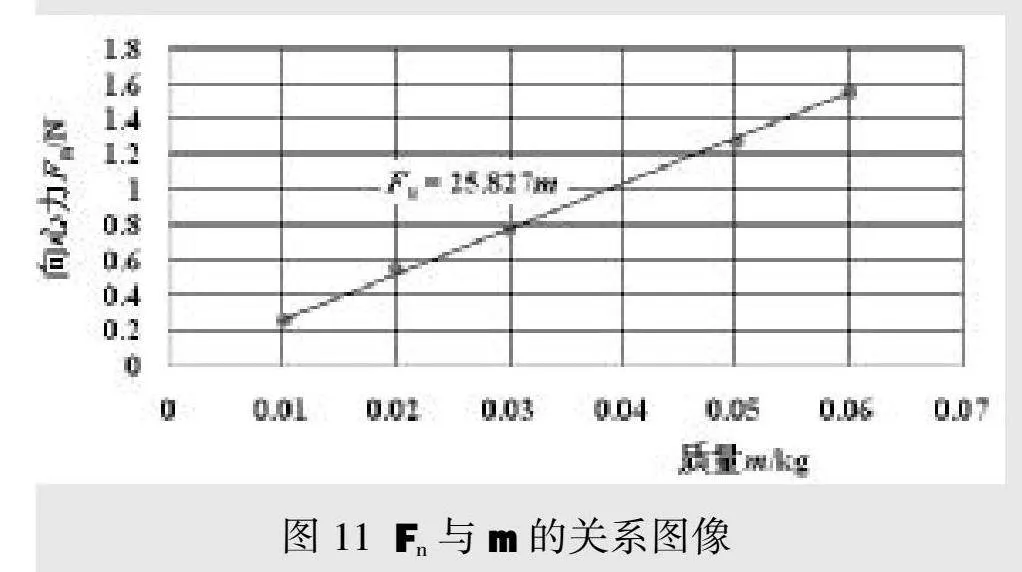
3.当 r=0.11m，ω=15rad/s时，Fn与m测量数据如表6，拟合图像如图11。

综合分析以上实验数据和拟合后的图像，可以得出结论，向心力大小的定量关系为Fn∝mrω2。由此可以看出，传感器可以测量多组具体数据，完成精确的定量探究。利用以上数据确定比例系数k等于1。因此向心力大小的定量表达式为Fn=mrω2。

以上三个层次的实验设计，实现了从定性感知到半定量探究再到精确定量探究，层层递进，突破了以往不能精确定量探究的难点。学生在实验探究过程中，充分体验并完成了挑战性的任务，同时增强了对科学本质的认识，最终得到向心力大小的定量表达式。

三、总结

本节课的创新实验设计，坚持立德树人、正确引导、形成能力、发展素养的原则，促使学生学习物理知识同时，建立物理观念，培养物理思维与探究精神，真正体会科学的本质。