盾构下穿古城区地面沉降预测及现场监测分析

摘 要：【目的】为了获取武汉市和平大道南延线盾构段地面的沉降数据，本研究通过Peck公式对现场沉降监测结果进行了拟合分析，并对Peck公式进行了修正。【方法】每30 m设置沿隧道上部对称分布的监测点进行现场地表沉降监测，选取其中4个最具代表性的断面沉降结果进行Peck公式拟合分析和验证，并根据实际沉降情况对Peck公式进行修正。【结果】研究结果表明，在隧道轴线上部存在异常沉降，因此通过对后续掘进段掘进参数进行调整，加强壁后同步注浆和监控测量控制沉降，并且将得到的沉降槽曲线与Peck公式进行拟合，得到4个断面的实测沉降数据与拟合曲线的拟合优度R2均高于0.85。【结论】盾构段沉降槽曲线与Peck公式计算结果高度拟合，可以用Peck公式对研究区沉降进行预测，选取地层体积损失率[Vl]为0.95%，沉降槽宽度系数k为0.55对Peck公式进行修正后，可以更加简单高效地预测后续沉降。

关键词：盾构；现场监测；地表沉降预测；Peck公式；沉降控制

中图分类号：U231.3 文献标志码：A 文章编号：1003-5168（2024）17-0050-06

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.17.011

Ground Subsidence Prediction and On-Site Monitoring Analysis of Shield Tunneling Under the Ancient City

ZHANG Xiang1 LI Yixiang2，3 CHEN Jian2，4 LIU Bin5 SHU Jicheng3

（1.Wuhan Municipal Engineering Quality Supervision Station， Wuhan 430015， China; 2.China Railway 14th Bureau Group Co.， Ltd.， Jinan 250101， China; 3.China Railway 14th Bureau Group Shield Engineering Co.， Ltd.， Nanjing 210000， China; 4.China Railway Construction Underwater Tunnel Engineering Laboratory， Jinan 250101， China; 5.State Key Laboratory of Geotechnical Mechanics and Engineering， Chinese Academy of Sciences，Wuhan 430071， China）

Abstract： [Purposes] In order to obtain the ground subsidence law of the shield tunneling section of the South Extension of Heping Avenue in Wuhan City， this paper conducted fitting analysis of the field settlement monitoring results through the Peck formula， and revised the formula. [Methods] A monitoring point symmetrically distributed along the upper part of the tunnel is set every 30 m for on-site surface settlement monitoring. Four of the most representative section settlement results are selected for Peck formula fitting analysis， and the Peck formula is verified. The Peck formula is modified based on the actual settlement situation. [Findings] It shows that there is abnormal settlement at the upper part of the tunnel axis. Therefore， the settlement is controlled by adjusting the excavation parameters of the subsequent excavation section， strengthening the synchronous grouting behind the wall and monitoring measurement， and the settlement trough curve obtained is matched with the Peck formula. The goodness of fit R2 between the measured settlement data of the four sections and the fitting curve is higher than 0.85. [Conclusions] The high fit between the settlement groove curve of the shield tunnel section and the Peck formula calculation results can be used to predict the settlement in Wuhan area. Choosing a stratum volume loss rate of 0.95% and a settlement groove width coefficient of 0.55 can make the Peck formula more simple and efficient in predicting subsequent settlement after correction.

Keywords： shield; on-site monitoring; surface subsidence prediction; Peck formula; settlement control

0 引言

近年来，随着我国城市建设的发展，地铁隧道逐渐增多。由于城市内部人口密集、建筑物众多，施工过程中难免会给城市正常运行带来的影响，盾构法因其安全、环保、高效、对周围环境影响小等优势，受到了众多业内人士的青睐［1-4］ 。

但是，不管盾构施工技术如何优化，施工过程对周围地层的扰动都是无法避免的［5］，尤其是盾构施工开挖会使上部地表发生沉降［6-7］。为此，相关学者对其进行了大量的研究，在众多研究成果中最早形成体系且认可度最高、应用面最广的是Peck公式［8］。通过对大量工程进行现场沉降监测研究发现，在盾构开挖过程中产生的沉降槽在径向截面上与高斯分布曲线高度相似，为了验证这一经验公式，许多学者在不同地区针对不同地质条件进行了大量现场监测，并根据不同施工项目针对现场情况对Peck公式进行了参数调整，使其更符合实际沉降，从而达到对类似隧道工程现场沉降进行预测的效果［9-15］。除了通过经验公式来预测沉降的手段，张海波等［16］提出了一种可以综合考虑多种因素的三维非线性有限元模拟方法；孙钧等［17］采用人工智能神经网络技术对地表沉降进行了预测；张建华等［18］对数值模拟和现场实测数据进行比较分析，发现实测沉降存在一定的滞后性；吕培林等［19］通过对沉降的时间历程、施工各阶段沉降量所占比例和地面沉降槽特征等3方面进行分析研究，得出了地面沉降主要由后续沉降量所决定的结论。

目前，对地面沉降的分析还是以经验公式、有限元模拟和现场监测为主，但是现场干扰因素众多，很难在模拟中体现出来，所以得到的模拟结果和实际结果可能出现较大差异。另外，采取有限元模拟预测，耗时长而且不能及时和现场监测数据相结合进行调整实现动态监测，由于经验公式的使用较为简便且经过了大量工程的应用和验证，可靠度较高。

因此，本研究通过将选出的4个典型断面采用Peck公式对现场监测数据进行非线性拟合，并根据拟合结果计算得到的经验参数进行修正，使修正后的Peck公式更符合武汉地区的地质条件和沉降特征，并对支护技术参数调整起到指导作用，从而达到通过简单高效的经验公式计算方法对后续盾构段的掘进进行预测的目的。

1 工程概况

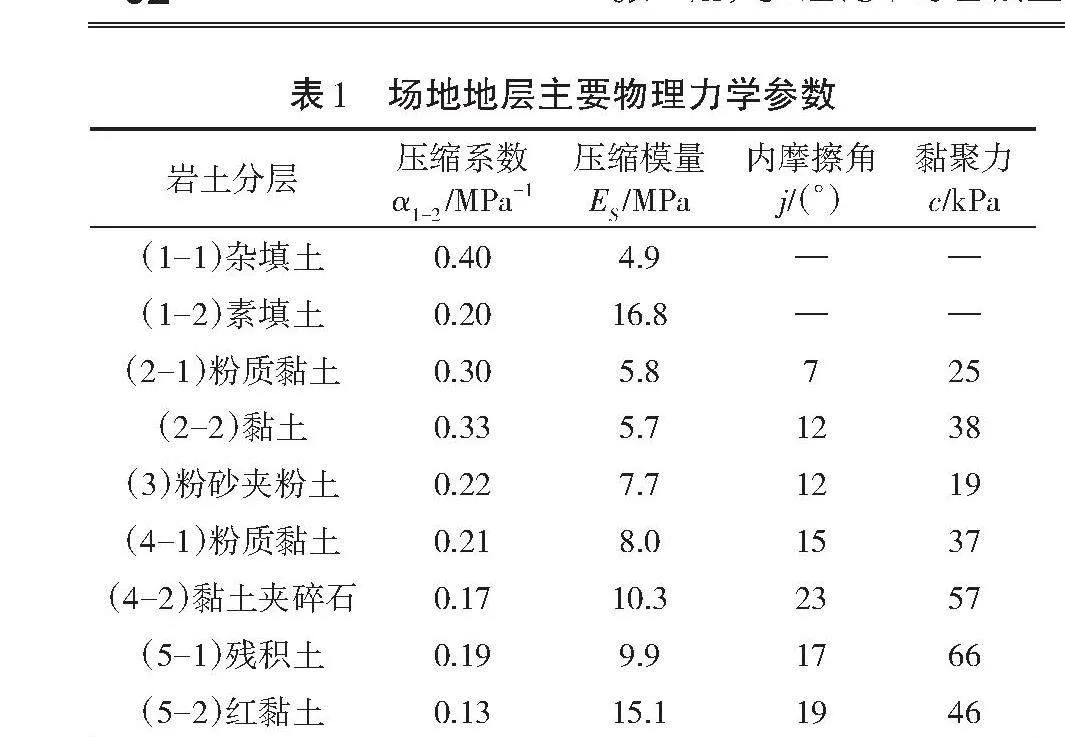
武汉和平大道南延工程路线全长3 042.5 m，其中盾构隧道段长1 390 m，采取单管双层并行的方案。线路与在建地铁线路平行，沿线下穿蛇山、黄鹤楼景区及老城区等沉降控制要求较高的区段。区间设计里程长1 390 m，最大纵坡4.5%，平面曲线最小半径为700 m，本区间线路埋层较深，隧道顶覆土厚度为11～54 m（蛇山底部）。盾构隧道穿越黏性土、泥岩、页岩、灰岩、硅质岩、石英砂岩等地层，主要物理力学参数见表1。管片为单层装配式衬砌，管片内径为14.2 m，外径为15.4 m，管片厚度为600 mm，环宽2 m，通用楔形环，楔形量为80 mm，采用强度等级C60，抗渗等级P12。衬砌圆环分为10块，结构形式为7（标准块）+2（邻接块）+1（K块），错缝拼装，每个环缝采用30个M36螺栓，每环纵缝采用28个M36螺栓。该隧道侧穿长江大桥下桥匝道、九龙井小区、下穿武珞路、黄鹤楼、民主路、中南神学院、粮道街、武汉三十三中及武昌古城区，建筑物密集且存在多处历史保护建筑等众多敏感区域，对盾构施工过程沉降控制要求较高，施工难度较大。

2 现场沉降监测

2.1 监测内容

在施工过程中，采用高精度监测设备对盾构穿越段进行常态化沉降监测，以为工程动态化设计和信息化施工提供所需的数据，从而使工程处于受控状态，确保工程本身及周边环境的安全，本次监测目标是以隧道为轴线呈对称分布的地表沉降。

2.2 监测设备及布设方案

地表沉降观测采用几何水准测量方法，使用天宝DiNi03电子水准仪进行观测和记录。纵向测点沿盾构推进轴线设置，每30 m布设一组横向沉降槽断面。沉降槽监测断面横向宽度和隧道下层车道线呈45°的夹角，监测点由线路中心向外由密到疏布置。监测点观测按《工程测量规范》（GB 50026—2007）中二等垂直位移监测网技术要求观测，采用闭合水准路线时可以只观测单程，采用复合水准路线形式必须进行往返观测，取两次观测高差中数进行平差，盾构法地表监测点示意如图1所示。

2.3 监测数据采集和沉降控制警报

观测完成后形成原始电子观测文件，通过数据传输处理软件传输至计算机，检查合格后使用专业水准网平差软件进行严密平差，得出各点高程值，沉降控制警报见表2，沉降量计算见式（1）。

[Δ]H=Hn-H0 （1）

式中：[Δ]H为监测点沉降量，mm；H0为监测点初始高程，mm；Hn为实测高程，mm。

2.4 支护技术参数计算

2.4.1 出渣量计算。由于盾构机的特殊构造，使其无法观察掌子面的情况，只能通过出渣量的多少来推算掌子面情况，出渣量过大掌子面可能会出现塌方，所以必须控制好出渣量。

每环土体实际开挖方量的计算见式（2）。

[V虚=η1π（D/2）2L] （2）

式中：D为开挖直径，取16.03 m；L为管片宽度，取2 m；η1为松散系数1.25～1.30（经验值）。通过计算得出，土量控制在510～520 m³为宜。

2.4.2 注浆量计算。

①注浆压力设定为0.3～0.5 MPa，管片注浆口的实测注浆压力为0.2～0.4 MPa。

②注浆量。理论注浆量的计算见式（3）。

[V注=π（R2−r2）L] （3）

式中：R为刀盘半径；r为开挖半径；L为管片宽度。实际的注浆量为理论建筑空隙的130%，即为36.5 m3。

③二次注浆。区间盾构侧穿施工过程中，应及时进行同步注浆及二次补充注浆，并合理控制注浆量及注浆压力。二次补浆量不小于同步注浆量的10%，即每环注浆量为4.7～5.5 m3，注浆压力控制在0.2～0.6 MPa。注浆过程中应加强监测，结合直通线自动化监测结果，控制注浆量及注浆压力，防止既有线路的沉降或隆起变形。

④克泥效注入。克泥效注入量根据开挖范围与盾尾之间的间隙量确定，每环的间隙量计算见式（4）。

V克=3.14×（2-R盾尾2）/4×2 （4）

式中：R盾尾为盾构机尾部半径，计算得到克泥效注入量每环不小于8.6 m³。

3 现场测试结果及拟合情况

本研究在监测断面中选取4个具有代表性的断面分别为X1+1903.86、X1+1853.20、X1+1802.86、X1+1763.51进行沉降结果分析，并通过Origin软件对这4个断面的监测数据进行非线性曲线拟合，具体如图2所示。通过得到的拟合优度R2的大小对隧道沉降槽与Peck公式的拟合程度进行判定。

根据现场沉降数据显示，沿隧道横向对称布置的地表沉降监测点表现为从两边向中间呈非线性逐渐加深，在距轴线距离左右5 m处发生急剧沉降，直至隧道正上方处沉降达到峰值，最大沉降值均未超过沉降控制警报值，由此可以认为沉降槽沿隧道中线对称分布，测点离隧道中心线越远，沉降量越小，盾构推进对地表的影响范围基本在隧道中心线两侧20 m的范围内。根据Peck公式拟合结果显示，在盾构穿越断面X1+1903.86 时最大沉降深度为5.6 mm，沉降槽宽度系数i为12.1 m；断面X1+1853.20最大沉降深度为5.1 mm，沉降槽宽度系数i为11 m；断面X1+1802.86最大沉降深度为6.5 mm，沉降槽宽度系数i为15.3 m；断面X1+1763.51最大沉降深度为6.2 mm，沉降槽宽度系数i为13.6 m。根据预设警报值-30～10 mm判定沉降处于正常范围。从现场监测数据中可以观测到在隧道正上方部分沉降相较于整个沉降槽有明显的沉降加剧现象，但就整体而言拟合优度R2均大于0.85，说明这4个断面处沉降槽形状与Peck公式计算结果的沉降曲线拟合效果较好，但是为了更准确地进行预测，需要对Peck公式进行进一步修正。

4 沉降预测

4.1 理论计算

在盾构穿越复杂地层变形敏感古城区时对沉降控制的要求极高，除了对前期进行评估还需要对整个过程进行实时监测和下一阶段进行预测。为了方便高效，本研究选择采用Peck经验公式对沉降进行预测，其表达式见式（5）和式（6）［8］。

[s=smaxexp[−x22i2]] （5）

[smax=Vsi2π] （6）

式中：s为沉降值；[smax]为沉降的最大值，位于沉降曲线的对称中心上；x为从沉降曲线中心到所计算点的距离，单位均为mm；[i]为从沉降曲线对称中心到曲线拐点（反弯点）的距离，一般称为“沉降糟槽宽度”，m；[Vs]为隧道单位长度地层损失，m3/m ，见式（7）。

[Vs=VlπR24] （7）

式中：[Vl]为地层体积损失率，即单位长度地层损失占单位长度盾构体积的百分比；R为盾构外机开挖直径。通过对大量地表沉降数据和有关工程资料进行分析后，得出式（8）。

[i=Z2πtan（45°−β2）] （8）

式中：[i]为沉降槽宽度系数，m；Z为隧道深度， m；β为隧道周围地层内摩擦角，°。其中[Vl]决定了沉降槽的竖向深度，而[i]则决定了沉降槽的横向宽度，但是由于在不同地质条件和地层分布下这两个参数也各不相同，因此国内外诸多学者展开了大量的研究，通过考虑更多现场实际相关参数进行改进，使其更具普适性，能够应用于诸多不同工程［20］。其中Clough等［21］基于隧道埋深及隧道半径，针对饱和黏性土提出了一种新的方法，来计算[i]值；Attewell等［22］在这基础上将工程的地层特性考虑进去，进一步使[i]值更贴近实际值；刘建航等［23］在Peck经验公式计算i值的基础上将选取的附近地层内摩擦角修改为选取上部多层土内摩擦角的加权平均值，将隧道上部多层土因素考虑进去；O' Reilly等［24］提出i的取值与隧道轴线埋深Z近似呈线性关系，即式（9）。

i=k·Z （9）

式中：Z为隧道轴线的埋深；k为沉降槽宽度系数，这进一步简化了k的取值。

4.2 Peck公式修正

通过将现场监测数据曲线与Peck公式进行拟合发现整体拟合度优度R2均大于0.85，说明使用Peck公式对该隧道掘进过程中的横向沉降进行预测是完全可行的，但是为了使Peck公式能够更加适用于武汉地区地层分布的沉降预测，还需要对其进行修正。

将4个断面的拟合结果代入式（6）、式（7）和式（9）可以计算得到4个断面处分别的地层体积损失率[Vl]和沉降槽宽度系数k，如图3所示。修正后计算结果与实测结果对比如图4所示。

由图3中可知，4个断面处地层体积损失率[Vl]取值为0.7%～1.2%，沉降槽宽度系数k的取值为0.5～0.6，为了使Peck公式更适应于对武汉地区的地层分布情况进行沉降预测，选取地层体积损失率[Vl]为0.95%，沉降槽宽度系数k为0.55进行沉降预测计算，得到的结果与实测结果进行对比明显更契合实际沉降曲线，这说明对Peck公式所选取的参数进行修正后的修正公式更能适应于武汉地区的沉降预测。

5 结论

本研究通过将现场监测数据与Peck公式计算结果进行拟合，分析结果可以得出沉降槽形状与拟合优度均高于0.85，说明采用Peck公式来预测沉降是完全可行的，并且根据现场地层情况调整参数对Peck公式进行修正后与实际沉降曲线拟合度更高，从而实现对后期掘进中的沉降预测及沉降控制。

针对隧道轴线上部左右5 m处出现的异常沉降，需要对支护技术参数进行修正并加强监测频率，及时采集沉降数据并对异常沉降采取应对性措施，以防止局部沉降异常情况发生。

参考文献：

［1］顾岷.我国城市轨道交通发展现状与展望［J］.中国铁路，2011（10）：53-56.

［2］施仲衡，王新杰，沈子钧.解决我国大城市交通问题的根本途径：稳步发展地铁与轻轨交通［J］.地铁与轻轨，1996（1）：2-5.

［3］何川，封坤，方勇.盾构法修建地铁隧道的技术现状与展望［J］.西南交通大学学报，2015，50（1）：97-109.

［4］朱牧原，魏力峰，方勇，等.超大直径盾构隧道下穿黄河大堤沉降分析与控制研究［J］.现代隧道技术，2022，59（3）：211-219.

［5］黄宏伟，张冬梅.盾构隧道施工引起的地表沉降及现场监控［J］.岩石力学与工程学报，2001（S1）：1814-1820.

［6］辛韫潇.盾构地铁隧道建设对地表文物建筑的影响研究［J］.工程勘察，2021，49（2）：1-6，30.

［7］杨开忠.西安地铁建设中的古建筑保护研究［D］.北京：中国地质大学（北京），2009.

［8］PECK R B.Deep excavations and tunneling in soft ground［J］.Proc. of 7th ICSMFE， Mexico，1969.

［9］孙建，王旭春，杨怀远，等.上软下硬地层下盾构法施工的Peck预测公式修正［J］.低温建筑技术，2019，41（10）：112-116.

［10］LI Y X，LIN J C，YAN S H，et al. Modification of the peck formula for a double-track shield tunnel under expressway subgrade［J］. Symmetry，2022，14（9）：1904-1904.

［11］TANG X W，LIANG J X，LIU W，et al. Modification of peck formula to predict ground surface settlement of twin tunnels in low permeability soil［J］.Advances in Civil Engineering，2021.

［12］ZHANG Q J，WU K，CUI S S，et al. Surface settlement induced by subway tunnel construction based on modified peck formula［J］. Geotechnical and Geological Engineering，2019，37（4）：2823-2835.

［13］ZHANG Z G，CHEN J，ZHANG M X，et al. Modified peck method of evaluating tunnelling-induced ground movements based on measured data［J］.Arabian Journal of Geosciences，2022，15（9）.

［14］姚爱军，赵强，管江，等.基于北京地层地铁隧道施工的Peck公式的改进［J］.地下空间与工程学报，2010，6（4）：789-793.

［15］段绍伟，黄磊，鲍灶成，等.修正的Peck公式在长沙地铁隧道施工地表沉降预测中的应用［J］.自然灾害学报，2015，24（1）：164-169.

［16］张海波，殷宗泽，朱俊高.地铁隧道盾构法施工过程中地层变位的三维有限元模拟［J］.岩石力学与工程学报，2005（5）：755-760.

［17］孙钧，袁金荣.盾构施工扰动与地层移动及其智能神经网络预测［J］.岩土工程学报，2001（3）：261-267.

［18］张建华，王宏伟，陈培新，等.杭州地铁4号线盾构下穿电力隧道直接切桩沉降分析［J］.工程力学，2022，39（S1）：144-152.

［19］吕培林，周顺华.软土地区盾构隧道下穿铁路干线引起的线路沉降规律分析［J］.中国铁道科学，2007（2）：12-16.

［20］罗兴财，周小文，张盛红.盾构施工地层损失控制方法及实例［J］.土木工程与管理学报，2022，39（2）：12-18.

［21］CLOUGH G W，SCHMIDT B.Design and performance of excavations and tunnels in soft clay［J］.Develop-ments in Geotechnical Engineering，1981，20，567-634.

［22］ATTEWELL P B， YEATS J， SELBY A R. Soil Move-ments Induced by Tunnelling and Their Effects on Pipe-lines and Structures［M］. Glasgow：Blackie，1986.

［23］刘建航，侯学渊.盾构法隧道［M］.北京：中国铁道出版社，1991.

［24］O' RELLY M P， NEW B M. Settlement above tunnels in the United Kingdom- their magnitude and prediction［J］.Tunnelling，1982：173-181.

收稿日期：2023-04-03

基金项目：山东省自然科学基金面上项目（ZR2023ME048）；泰山产业领军人才工程专项经费资助（tscx202306015）；中国铁建科研开发计划（2023-B04）；中铁十四局科技研发计划项目（9137000016305598912021A01）。

作者简介：张翔（1985—），男，本科，高级工程师，研究方向：市政建筑。

通信作者：李义翔（1988—），男，本科，高级工程师，研究方向：市政交通。