玻烈河水库面板堆石坝三维静动力有限元分析

摘 要：【目的】研究地震作用下堆石坝应力变形规律，为面板堆石坝抗震设计提供依据。【方法】结合玻烈河水库面板堆石坝结构特性和材料特性，开展三维静动力有限元分析。采用邓肯-张E-B模型描述堆石体静力特性，以及等效非线性黏弹性模型描述堆石体动力特性。【结果】静力计算结果表明，蓄水期坝体的最大垂直位移是最大坝高的0.45%，坝体最大应力在合理范围内。动力计算结果表明，加速度响应坝体顺河向、横河向、垂直方向均较强烈。永久沉降约为坝高的0.33%，坝体整体稳定。【结论】分析结果表明，玻烈河水库面板堆石坝设计满足规范要求，设计合理。

关键词：面板堆石坝；静动力分析；应力变形

中图分类号：TV641.4；TV312 文献标志码：A 文章编号：1003-5168（2024）17-0041-05

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.17.009

Three-Dimensional Static and Dynamic Finite Element Analysis of

Concrete Face Rockfill Dam of Boliehe Reservoir

TAN Zhuo1 ZHANG Han2

（1.Chongqing Water Conservancy and Electric Power Construction Survey， Design and Research Institute

Co.， Ltd.， Chongqing 404100， China; 2.China Water Resources Beifang Investigation Design and Research

Co.， Ltd.， Tianjin 300222， China）

Abstract： [Purposes] This paper studies the stress deformation law of rockfill dam under earthquake action to provide guidance for the seismic design of concrete face rockfill dam. [Methods] Three-dimensional static-dynamic finite element analysis was conducted， considering the structural and material characteristics of the Baolie River Reservoir concrete face rockfill dam. The Duncan-Zhang E-B model was utilized to describe the static properties of the rockfill， while an equivalent nonlinear viscoelastic model was employed to characterize its dynamic behavior. [Findings] Static calculations indicate that the maximum vertical displacement of the dam body during the reservoirfilling period accounts for 0.45% of the maximum dam height， and the maximum stress in the dam body falls within a reasonable range. Dynamic calculations reveal that the dam body experiences stronger acceleration responses in the downstream， transverse， and vertical directions， with a permanent settlement of approximately 0.33% of the dam height， ensuring overall stability of the dam body. [Conclusions] Analysis results demonstrate that the design of the concrete face rockfill dam in the Baolie River Reservoir meets regulatory requirements and is technically sound.

Keywords： concrete face rockfill dam; static and dynamic analysis; stress deformation

0 引言

堆石坝因适应能力强、环境友好、抗震性能强，成为诸多水库建设的首选［1］。随着坝工技术的进步，我国茨哈峡、古水、马吉等水库相继规划建设了多个堆石坝工程［2］。西部地区是地震活跃地带，强震作用下堆石坝抗震性能值得关注。因此，对西部地区新建面板堆石坝开展静、动力条件下应力变形分析，是保证堆石坝工程建设和安全运行的重要前提。

数值模拟是堆石坝静动力分析和估计坝体永久变形的常用方法，合理的参数选取和适宜的本构模型是开展堆石坝精细化数值模拟的重要前提。杨启贵等［3］通过研究水布垭面板堆石坝的变形监测资料，分析了水位周期性循环荷载对堆石坝长期变形的影响。邹德高、何亮等［4-5］了开展了基于广义塑性模型的面板堆石坝数值模拟。胡圣明等［6］对300 m级高黏土心墙堆石坝进行了静动力分析。根据前人的研究可知，准确了解面板堆石坝静动力作用下坝体形态对堆石坝安全运行至关重要。

本研究采用邓肯-张E-B模型，对玻烈河水库面板堆石坝工程进行三维非线性静动力有限元模拟计算，分析该面板堆石坝在水荷载和地震作用下的沉降变形和动力响应，研究玻烈河水库面板堆石坝的变形演化规律，为该大坝结构设计和优化提供依据。

1 计算原理及方法

1.1 坝体静力模型本构

坝体堆石采用邓肯-张E-B模型，混凝土、基岩均采用线弹性本构模型。E-B模型中，需确定c、△φ、φ0、K、n、Rf、Kur、Kb、m共8个参数。E-B模型对应切线弹性模量Et与体积模量Bt及回弹模量Eur见式（1）、式（2）、式（3）。

[Et=d（σ1-σ3）dε1=Ei（1-RfS）2] （1）

[Bt=Kbpaσ3pam] （2）

[Eur=Kurpaσ3pam] （3）

式（1）中：S为应力水平，为实际主应力差与破坏时主应力差的比值，即式（4）。

[S=σ1-σ3（σ1-σ3）f] （4）

根据摩尔-库仑破坏准则可得式（5）、式（6）。

[（σ1-σ3）f=2σ3sinφ+2Ccosφ（1-sinφ）] （5）

[σ1-σ3=εaa+bεa] （6）

以上式中：a、b为试验常数；σ1为轴向压力；σ3为试件围压；εa为轴向应变。

内摩擦角φ随围压σ3的变化而变化，表达式见式（7）。

[φ=φ0-Δφlgσ3pa] （7）

式中：φ0表示初始内摩擦角；Δφ为围压增加时内摩擦角减小值（单个对数周期）。

1.2 混凝土、基岩计算模型

混凝土、基岩等均采用线弹性模型，即式（8）。

[Δσ=DΔε] （8）

式中：｛Δσ｝=［Δσx Δσy Δσz Δτxy Δτyz Δτzx］T；｛Δε｝=［Δεx Δεy Δεz Δγxy Δγyz Δγzx］T；［D］为弹性矩阵，见式（9）。

[D=λ+2Gλλ000λλ+2Gλ000λλλ+2G000000000000G000G000G] （9）

式中：[λ=Eμ（1+μ）（1-2μ）]；[G=E2（1+μ）]；[E]为弹性模量；[μ]为泊松比。

1.3 接触面模型

该模型区别于普通实体单元，为模拟接触面错动、滑移、开裂等现象，选用无厚度Goodman单元为接触单元。该模型以八结点六面体无厚度接触为基本单元，六结点五面体无厚度接触面单元为填充单元。周边缝和面板垂直缝采用基于无厚度Goodman单元的连接单元模型进行模拟。

1.4 动力本构模型

本研究采用等效非线性黏弹性开展动力计算，坝料和地基材料假定为黏弹性，等效剪切模量G和等效阻尼比λ反映土体动应力应变关系。通过计算确定最大动剪切模量Gmax与平均有效应力σ0'的关系，以及G与λ的关系。动剪切模量表达式见式（10）。

[Gd=11+γd/γrGmax] （10）

动剪应变表达式见式（11）。

[λ=λmaxγd/γr1+γd/γr] （11）

初始最大动剪切模量表达式见式（12）。

[Gmax=K'paσ'mpan] （12）

参考剪应变见式（13）。

[γr=τmaxGmax] （13）

以上式中：λmax、K'、n等3个参数由动三轴试验确定。

1.5 永久变形本构

本研究采用沈珠江模型计算坝体残余应，动力残余体积应变增量[Δεv]和残余剪切应变增量[Δγs]，分别按式（14）和式（15）计算。

[Δεv=c1γdc2exp（-c3S12）ΔNL1+NL] （14）

[Δγs=c4γdc5S12ΔNL1+NL] （15）

式中：[ΔNL、NL]为等效振动次数的增量和累加量；[c1、c2、c3、c4、c5]分别为5个动力残余变形试验参数。

2 计算实例

玻烈河水库面板堆石坝最大坝高约120 m，坝轴线长约280 m。挡水坝级别为2级，正常蓄水位为1 610.0 m、设计洪水位为1 610.10 m、校核洪水位为1 611.01 m。建模垂直方向坝基取至高程1 334 m，顺河向自坝轴向下游侧延伸460 m，自坝轴向上游侧延伸350 m。计算坐标系规定为顺河向为X轴；坝轴向为Y轴；竖向为Z轴。工程区平均坡比近似坝体下游。本研究按照剖面形式设计面板、垫层、堆石体分区。坝体垫层料、过渡料、堆石料采用邓肯-张E-B模型，混凝土和坝基岩体采用线弹性模型，接触面采用Goodman模型，趾板与面板之间、面板与防浪墙之间、防浪墙间及面板间接缝采用接缝模型，材料参数见表1、表2。动力有限元分析计算工况及荷载组合见表3。

3 静动力分析结果

3.1 静力计算结果

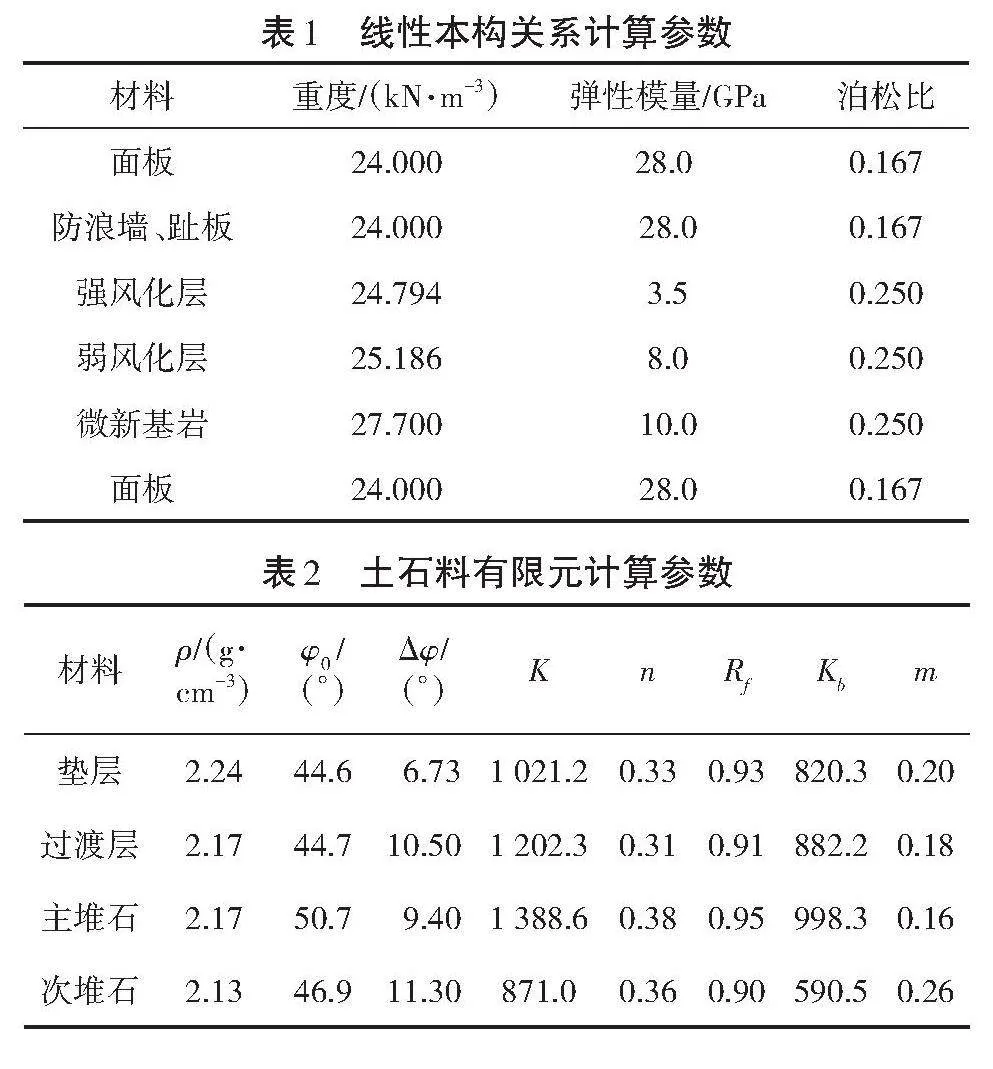
正常蓄水位典型断面应力如图1所示。图1中，Z为坝高，X为顺河向坐标，下同。由图1可知，应力随高程的降低逐渐增大，各断面应力水平不高，坝体内未出现明显剪切破坏区。典型断面顺河向指向上游最大水平位移为-185.0 mm，顺河指向下最大水平位移为210.0 mm，且位于坝体下游侧次堆石区中下部附近区域。坝体最大垂直位移为-420.0 mm，为最大坝高的0.43%，发生在坝轴线下游12 m、0.5倍坝高附近。

竣工期典型断面位移情况如下。正常蓄水位工况下，坝体最大垂直位移为-441.5 mm，为最大坝高的0.45%；坝体顺河向水平位移整体倾向下游，顺沟谷指向下游的最大水平位移为289.4 mm，指向上游最大水平位移为-78.8 mm；坝轴线断面上，右岸堆石总体向左岸位移，坝轴向指向左岸最大水平位移为43.8 mm，左岸堆石体总体向右岸位移，指向右岸的最大水平位移为-57.5 mm。在蓄水过程中，坝体位移随蓄水位增高而增加。

3.2 动力计算结果

3.2.1 加速度响应。研究发现，坝体最大绝对加速度（顺河向）最大值为4.6 m/s2，坝体动力响应指标和原始地震指标的比值为3.62，位于下游坝坡；最大绝对加速度（坝轴向）最大值为2.7 m/s2，坝体动力响应指标和原始地震指标的比值为2.12，发生在下游坝坡；坝体最大绝对加速度（竖向）最大值为3.1 m/s2，坝体动力响应指标和原始地震指标的比值为3.40，发生在下游坝坡。坝体加速度响应在3个方向（顺河向、坝轴向、竖向）均较为强烈，河谷较深断面坝顶处反应最剧烈，河床部位反应差异不明显。由典型断面绝对加速度分布可知，上游坡加速度响应小于下游坡。

坝轴线断面最大绝对加速度顺河向最大值为4.6 m/s2，坝体动力响应指标和原始地震指标的比值为3.62，位于坝顶；最大绝对加速度坝轴向为2.7 m/s2，坝体动力响应指标和原始地震指标的比值为2.12，位于坝横y=180 m断面坝顶；坝体最大绝对竖向加速度最大值为3.0 m/s2，坝体动力响应指标和原始地震指标的比值为3.30，位于坝横y=150 m断面坝顶。

3.2.2 位移响应。坝轴线断面最大位移响应如图2所示。由图2可知，典型断面顺河向位移最大值为36.0 mm，位于坝顶位置。坝轴向最大位移在下游坝坡（x=11 m），为15.0 mm。从位移响应来看，竖向位移响应较小，整体位移不大。图2中顺河向（y=130 m断面坝顶）堆石体最大位移36.0 mm，坝轴向坝顶（坝横y=130 m断面）最大位移22.0 mm；竖向坝顶（坝横y=150 m）最大位移15.0 mm。表明坝轴线断面位移整体较小，顺河向位移最大，竖向位移最小。

3.2.3 应力响应。坝体典型断面堆石体应力响应分布如图3所示。由图3可知，第一主应力最大为295.6 kPa，第二主应力最大为135.7 kPa，第三主应力最大为91.8 kPa。与静力应力情况相比，地震期间坝体强度满足要求。该坝体最大动剪应力为163.7 kPa，坝体各单元不会产生动剪切破坏。

3.2.4 永久变形。坝体典型断面地震永久变形分布如图4所示。由图4可知，顺河向坝体产生向上游-10.0 mm的永久水平位移，指向下游261.7 mm；坝轴线向左岸位为70.2 mm，指向右岸位移为-87.5 mm；坝体永久沉降约为0.33%倍坝高，为-326.8 mm。

4 结论

①竣工期和蓄水期坝体最大垂直位移约占最大坝高的0.45%；坝体最大应力在合理范围内。应力变形计算结果与同级别坝体相当，符合一般规律，坝体设计合理。

②地震作用下，顺河向、坝轴线和垂直方向坝体加速度响应强烈。坝体最大断面加速度响应位于坝顶。加速度大小排序为顺河向>垂直向，地震永久沉降约为坝高的0.33%。

参考文献：

［1］温立峰，柴军瑞，许增光，等.面板堆石坝性状的初步统计分析［J］.岩土工程学报，2017，39（7）：1312-1320.

［2］孔宪京，张宇，邹德高.高面板堆石坝面板应力分布特性及其规律［J］.水利学报，2013，44（6）：631-639.

［3］杨启贵，王艳丽，左永振.水循环荷载作用下高面板堆石坝长期变形特性研究［J］.岩土工程学报，2024，46（6）：1339-1346.

［4］邹德高，徐斌，孔宪京，等.基于广义塑性模型的高面板堆石坝静、动力分析［J］.水力发电学报，2011，30（6）：109-116.

［5］何亮，李雄威.基于广义塑性模型的加筋面板堆石坝数值模拟［J］.水利水电技术，2020，51（1）：109-114.

［6］胡圣明，王铭明，汪晨，等.地震作用下加筋堆石坝稳定性分析［J］.水电能源科学，2021，39（12）：104-107，50.

收稿日期：2024-03-05

作者简介：谭倬 （1992—），男，本科，工程师，研究方向：水利工程安全防控；张涵（1991—），女，硕士，工程师，研究方向：水工设计。