上证综指与沪深300指数的流动性风险溢出研究

2024-10-08 00:00张文君

管理学家 2024年18期

[摘要]上证综指和沪深300指数作为重要的宏观经济指标，二者之间的流动性风险溢出是学者和投资者关注的重点问题。随着中国金融领域的不断发展，二者股票指数之间的联动性呈现出增强趋势。由于ADCC-EGARCH模型能够捕捉时间序列数据的条件持续期和波动性特征，文章对上证综指和沪深300指数两个股票指数的流动性风险溢出效应进行了深入分析，通过对2021年7月1日至2024年5月31日的基础数据进行实证研究，结果表明上证综指对沪深300指数的风险溢出逐渐趋于稳定，在市场出现压力的时期，二者指数之间存在显著的流动性风险溢出效应。研究结论为理解中国股票市场内的流动性风险相互影响提供了新的视角，对于我国金融市场的稳定和健康发展具有重要的理论和实践意义。

[关键词]沪深股票市场；流动性风险；ADCC-EGARCH；动态相关性

中图分类号：F832 文献标识码：A 文章编号：1674-1722（2024）18-0076-03

全球化的不断深入和新冠疫情的不断冲击，使我国金融市场内部的相互依赖性日益增强。在此背景下，我国作为全球较大的经济体之一，其经济活力指标股票市场表现不仅对本国经济产生深远影响，也对全球金融市场的稳定性具有举足轻重的作用[ 1 ]。

上证综指是我国股市最早的综合指数之一，沪深300指数综合反映了我国A股市场上市股票价格的整体表现[ 2 ]。流动性风险是金融市场健康稳定发展的基础，作为金融市场重要衡量指标之一，指的是以低成本快速购买或出售大量资产的能力[ 3 ]。在金融市场中，流动性风险的溢出效应尤为值得关注，因为它可能导致市场恐慌、资产价格波动甚至金融危机。

随着我国股票市场中互联互通关系的不断加深，市场间的流动性风险相互传染，导致中国股票市场内流动性风险的相关性增强。因此，了解上证综指与沪深300指数之间流动性风险的动态相关性，对于帮助投资者规避流动性风险和监管我国股票市场具有一定参考价值。随着金融市场的不断变化发展，学者们在流动性风险的定义和研究上也在不断深化。凯恩斯在1936年将市场流动性定义为市场价格将来的波动性。苏博从金融行业的角度研究流动性风险，提出金融科技行业的发展会在一定程度上导致商业银行的流动性风险增加[ 4 ]。殷高峰从全球流动性对中国的溢出的角度提出，全球流动性对金融市场资产泡沫的溢出效应增加会导致对实体经济通货膨胀的溢出效应减小[ 5 ]。何英等提出经济政策不确定性强化了跨境资本流动对中国银行流动性风险的提升效应[ 6 ]。雷彭涛借助随机森林模型分析商业银行的影响因素，利用SHAP值分析这些特征对流动性风险的具体影响方向[ 7 ]。关于金融市场风险溢出效应测度的研究吸引了国内外学者的广泛关注。学者们运用DCC-GARCH和CoVaR模型进行中国股票市场或金融市场之间的风险溢出研究[ 8 ]。林娟等使用时变CoVaR模型研究沪深股市和香港股市中的风险溢出程度[ 9 ]。很多学者通过DCCGARCH类模型计算出的动态相关性测度股票市场中的风险溢出程度。徐清海等使用DCC-MVGARCH模型分析以次贷危机时期为代表的中国金融市场之间的动态关系[ 1 0 ]。马小龙基于ADCC-GARCH模型论证了中国期货商品与上证综指之间的动态关系[ 1 1 ]。韩方园等对房地产业与三类商业银行分别拟合DCC-GARCH模型，研究两行业的动态相关关系和风险溢出关系[ 1 2 ]。

目前，关于流动性风险的研究大多集中在全球金融市场，关于中国股市内流动性风险溢出程度测度的文献相对较少，DCC-GARCH模型在探讨风险溢出程度方面也被广泛应用。

一、理论分析

（一）流动性风险指标构建

当前，学者们在流动性风险方面存在多个维度的测度，通过借鉴Amihud指标，从市场冲击的角度衡量市场流动性水平，该指标通过测量交易价格对成交量的敏感性，评估市场的流动性，即交易成本和市场冲击。随后邓思哲等通过对比分析多种指标，得出Amihud指标在交易成本与市场冲击上更能反映市场的流动性水平[ 1 3 ]。其计算公式如下：

其中，Ⅲij代表个股或资产i在时间j的流动性风险指标；Rij代表个股或资产i在时间j的价格变动，通常计算为该第j只股票指数在第i天的对数收益率；SOVLij代表个股或资产i在时间j的日交易总额。

（二）ADCC-EGARCH模型

ADCC-EGARCH模型是GARCH模型的扩展，它不仅能够捕捉时间序列的波动聚集现象，而且能处理多个时间序列之间的动态相关性，特别是当这种相关性随时间变化时[ 1 4 ]。

此外，该模型不但考虑了非对称效应，即正负冲击对波动性的影响可能不同，而且包含了长期波动性的成分，这有助于捕捉时间序列的长期特征。

因此，文章采用此模型分析沪深股票市场间流动性风险的动态相关关系。EGARCH模型是GARCH模型在多变量情况下的自然扩展。与GARCH模型类似，EGARCH模型不仅考虑了残差项平方的线性组合，而且包含了条件方差的平方项，以更准确地捕捉时间序列数据的波动性特征。EGARCH模型能够描述多个时间序列之间的动态相关性和相互影响。具体来说，GARCH（p，q）模型的条件方程可以表示为：

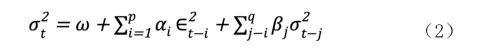
其中，σ2t是时间t的条件方差，ω是常数项，αi和βj是模型参数，∈t-i是滞后残差项，p和q是滞后阶数。

最后，ADCC-EGARCH模型通过动态条件相关（DCC）结构来估计相关系数矩阵，这允许相关系数随时间变化：

其中，Ht是条件协方差矩阵，Dt是对角矩阵，包含各时间序列的条件标准差，Rt是相关系数矩阵，B是长期均值矩阵，γi是衰减因子，m是衰减阶数。

二、实证分析

文章对选择的样本数据流动性风险进行波动性解释，通过各统计量对数据进行描述。此外，通过ADCC-EGARCH模型估计出的时变相关系数，分析上证综指和沪深3 0 0指数的风险溢出情况。

（一）样本选择与数据说明

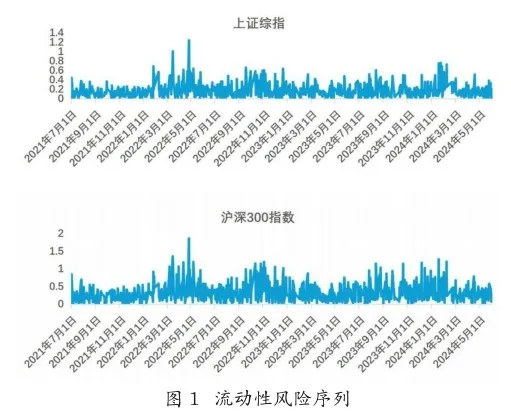
文章选取Choice数据库中的样本时间区间，选择2 0 2 1年7月1日到2 0 2 4年5月3 1日的上证综指和沪深3 0 0指数计算各自的Amihud流动性风险指标，共7 0 7个交易日数据。通过构建ADCC-EGARCH模型，探讨上证综指和沪深3 0 0指数流动性风险的时变相关性，处理后的两个股票指数的流动性水平序列波动情况如图1所示。

同时，表1给出了沪深股票数据流动性风险时间序列的描述统计量，给出了用于检验时间序列数据是否具有单位根（即是否为非平稳的）的ADF值。

首先，如McARIE47HQ5C5WEY852BxQ==表1所示，从均值来看，沪深3 0 0指数的流动性风险大于上证综指。从标准差来看，上证综指标准差较小。样本数据的偏度均大于0，为正偏，峰度均大于3，为尖峰，因此，上证综指和沪深3 0 0指数流动性风险序列具有尖峰、厚尾和非正态的特征。

其次，由于时间序列建模对于序列的平稳性要求很高，处理后的两个股票指数的流动性风险水平序列波动情况如图1所示。其中，每组流动性风险时间序列的波动幅度都较大，呈现出一定的尖峰后尾性质，也初步判断其分布不服从正态分布。

因此，文章进行平稳性检验，上述两只股票的收益率序列ADF检验p值均为0 . 0 1，拒绝原假设，均通过1 %置信水平下的平稳性检验，因而流动性风险序列都是平稳的，可用于后续的时间序列建模。

（二）时变相关性分析

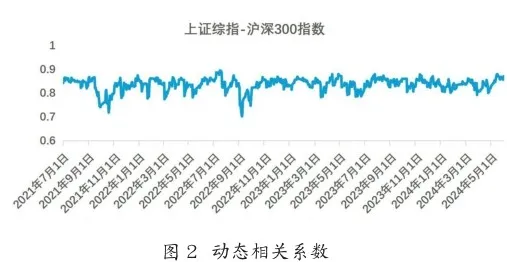
文章基于ADCC-EGARCH模型估计出的时变相关系数，画出2 0 2 1年7月1日至2 0 2 4年5月3 1日股票指数间流动性风险的条件动态相关系数图，如图2所示。

从图2可以看出，上证综指股票指数与沪深300指数间的动态相关关系呈现出波动较大的正相关性，且动态相关系数值大多集中在0.6以上，表明两市场间的动态相关关系较强但并不稳定。2022年9月7日之后，相关关系相较之前更加紧密，并逐渐趋于一种稳定的状态。总体来看，上证综指和沪深300指数之间的相关关系更加稳定，且具有一定的收敛性质。

三、结语

文章选取上证综指、沪深300指数计算两只股票指数的流动性风险，针对上证综指—沪深300指数的流动性指标，构建ADCC-EGARCH（1，1）模型，探讨两个市场间流动性风险的溢出效应。

通过实证研究得出以下结论：两只股票指数的非流动性指标具有波动幅度较大的现象，两个股票市场指数的非流动性样本时间序列不服从正态分布，呈现出尖峰后尾的特征，且存在明显的波动聚集性。上证综指—沪深300指数的流动性风险具有较强的动态相关性，在2022年9月7日后相关关系均表现为更加紧密，且动态相关性的波动逐渐趋于稳定。

因此，在我国股票市场流动性风险爆发前期应该给予足够的重视，设立股票市场风险监管部门。同时，将对流动性风险的预测和溢出进行日常风险管理，时刻掌握市场流动性指标的变化规律，尽可能地预防市场出现极端的流动性风险。