巧用一次函数分析电学实验系统误差

电学实验的系统误差分析是学生的重点、难点，甚至是痛点．如何快速地判断测量值比实际值大还是小呢？本文将巧用一次函数法来快速判断，即在数据处理时列出理想电表和实际电表对实验结果的函数关系，利用一次函数的斜率和截距就能快速地判断测量值和真实值的误差关系，此方法不仅能培养学生“运用数学工具解决物理问题”的能力，而且比解析法、等效法、列表法等方法更简便，以彰显数理结合的独特魅力．

一、伏安法测电阻

1.外接法

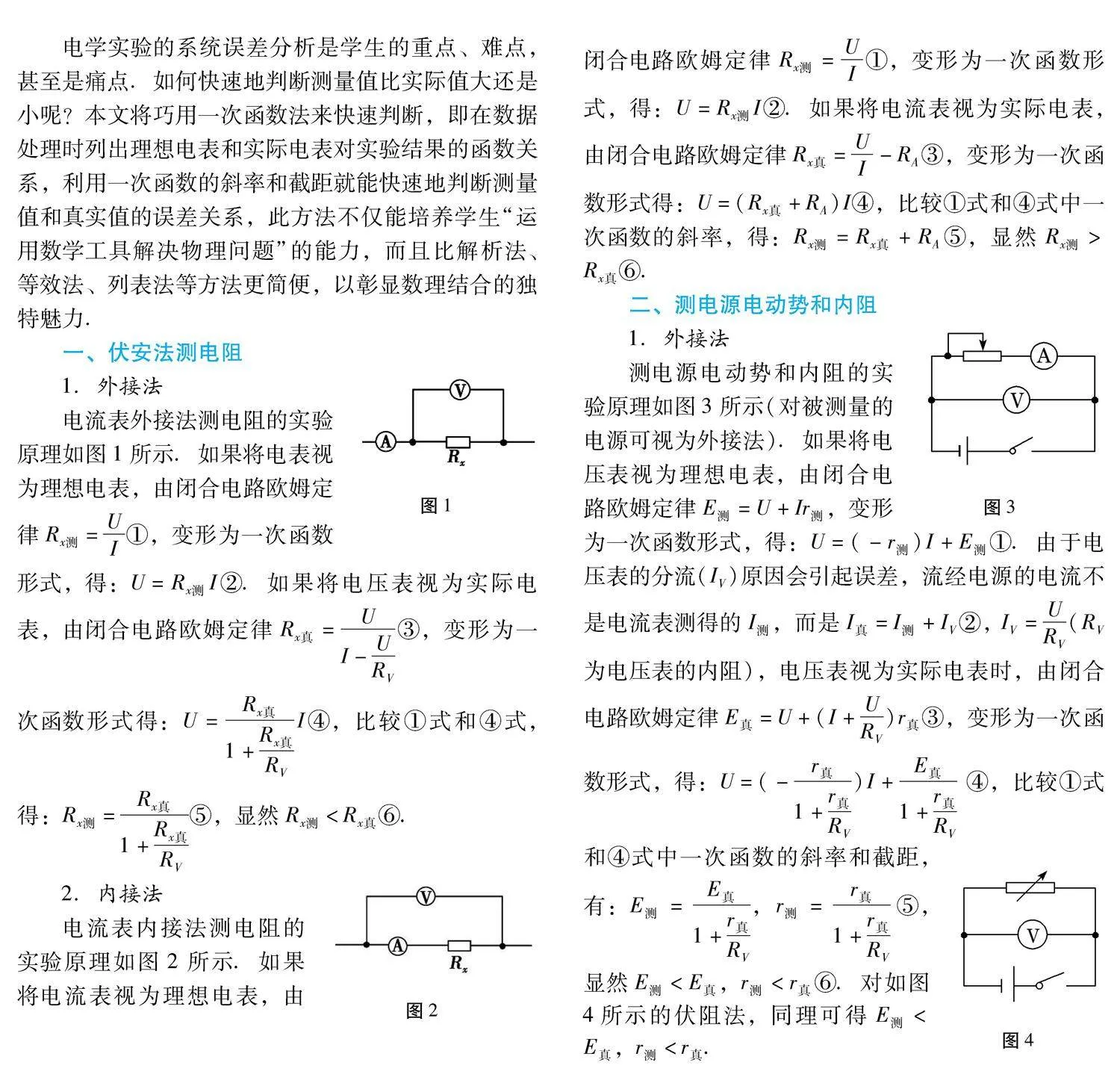
图1

电流表外接法测电阻的实验原理如图1所示．如果将电表视为理想电表，由闭合电路欧姆定律Rx测=UI①，变形为一次函数形式，得：U=Rx测I②．如果将电压表视为实际电表，由闭合电路欧姆定律Rx真=UI-URV③，变形为一次函数形式得：U=Rx真1+Rx真RVI④，比较①式和④式，得：Rx测=Rx真1+Rx真RV⑤，显然Rx测<Rx真⑥．

2.内接法

图2

电流表内接法测电阻的实验原理如图2所示．如果将电流表视为理想电表，由闭合电路欧姆定律Rx测=UI①，变形为一次函数形式，得：U=Rx测I②．如果将电流表视为实际电表，由闭合电路欧姆定律Rx真=UI-RA ③，变形为一次函数形式得：U=（Rx真+RA）I④，比较①式和④式中一次函数的斜率，得：Rx测=Rx真+RA⑤，显然Rx测>Rx真⑥．

二、测电源电动势和内阻

1.外接法

图3

图4

测电源电动势和内阻的实验原理如图3所示（对被测量的电源可视为外接法）．如果将电压表视为理想电表，由闭合电路欧姆定律E测=U+Ir测，变形为一次函数形式，得：U=（-r测）I+E测①．由于电压表的分流（IV）原因会引起误差，流经电源的电流不是电流表测得的I测，而是I真=I测+IV ②， IV=URV（RV为电压表的内阻），电压表视为实际电表时，由闭合电路欧姆定律E真=U+（I+URV）r真③，变形为一次函数形式，得：U=（-r真1+r真RV）I+E真1+r真RV ④，比较①式和④式中一次函数的斜率和截距，有：E测=E真1+r真RV，r测=r真1+r真RV⑤，显然E测<E真，r测<r真⑥．对如图4所示的伏阻法，同理可得E测<E真，r测<r真．

2.内接法

图5

图6

测电源电动势和内阻的实验

原理如图5所示（对被测量的电源可视为内接法）．如果将电流表视为理想电表，由闭合电路欧姆定律E测=U+Ir测，变形为一次函数形式，得：U=（-r测）I+E测①．由于电流表的分压（UA）原因会引起误差，电源两端的电压不是电压表测得的U测，而是U真=U测+UA②， UA=IRA（RA为电流表的内阻），电流表视为实际电表时，由闭合电路欧姆定律E真=U+I（r真+RA）③，变形为一次函数形式，得：U=-（r真+RA）I+E真④，比较①式和④式中一次函数的斜率和截距，有：E测=E真，r测=r真+RA⑤，显然E测=E真，r测>r真⑥．对如图6所示的安阻法，同理可得E测=E真，r测>r真成立．在以上两种测量电路中，内接法虽然测量的电源电动势准确，但电流表分压较为明显，所以内阻测量的误差很大；外接法虽然电动势和内阻测量均偏小，但是电压表内阻很大，分流不明显，所以电动势和内阻的测量误差较小，所以实验室一般选择外接法来减小由电表内电阻引起的系统误差．

三、半偏法测电表内阻

1.半偏法测电流表内阻

图7

半偏法测电流表内阻的实验原理如图7所示．根据实验原理，如果不考虑闭合S2后干路电流的变化，RA测=R2①，对实际电路，闭合S2前，由闭合电路欧姆定律，有：E=（r+R1+RA真）Ig ②，闭合S2后，有：E=12IgRA真+（12Ig+12IgRA真R2）（r+R1） ③，变形为一次函数形式，得：E=12［（r+R1）+RA真（r+R1+R2）R2］Ig④，比较②式和④式中一次函数的斜率，有：r+R1+RA真=12［（r+R1）+RA真（r+R1+R2）R2］⑤，化简得：RA真=r+R1r+R1-R2R2 ⑥，得出结论：RA测=R2<RA真 ⑦，且R1RA满足得越充分，系统误差越小．

2.半偏法测电压表内阻

图8

半偏法测电压表内阻的实验原理如图8所示．根据实验原理，如果不考虑断开S2后电压表所在支路电压的变化，RV测=R0①，对实际电路，断开S2前，由闭合电路欧姆定律，有：E=Ug+（UgRV真+UgRp1）（r+Rp2） ②，变形为一次函数形式，得：

E=1+（1RV真+1RP1）（r+Rp2）Ug ③，断开S2后，有：E=Ug2+Ug2RV真R0+Ug2+Ug2RV真R0Rp1（r+Rp2） ④，

变形为一次函数形式，得：E=

12+12RV真R0+12+12RV真R0RP1（r+Rp2）

Ug ⑤，比较③式和⑤式中一次函数的斜率，有：

1+（1RV真+1Rp1）（r+Rp2）=12+12RV真R0+12+12RV真R0Rp1（r+Rp2） ⑥，化简得：RV真=R0-2Rp1（r+Rp2）r+Rp2+Rp1 ⑦，得出结论：RV测=R0>RV真 ⑧，且RVR1满足得越充分，系统误差越小．

四、欧姆表测电阻

图9

欧姆表的实验原理如图9所示．由闭合电路欧姆定律，有：E=IgR内，E=I（R内+Rx测）①，变形为一次函数形式得：Ig=（1+Rx测R内）I ②，如果电池用久了，电动势变小，内阻变大，但仍然能调零，由闭合电路欧姆定律，有：E′=IgR′内，E′=I（R′内+Rx真） ③，变形为一次函数形式得：Ig=（1+Rx真R′内） I④，比较②式和④式中一次函数的斜率，有：Rx测=R内R′内Rx真⑤，得出结论：Rx测>Rx真，且定量计算误差的大小，有：Rx测Rx真=EE′=R内R′内成立⑥．

五、实例分析

【例1】（2024年湖南卷）某实验小组要探究一金属丝的阻值随气压变化的规律，搭建了如图10（a）所示的装置．电阻测量原理如图10（b）所示，E是电源，V为电压表，A为电流表．

图10

（1）保持玻璃管内压强为1个标准大气压，电流表示数为100 mA，电压表量程为3 V，表盘如图10（c）所示，示数为 V，此时金属丝阻值的测量值R为 Ω（保留3位有效数字）；

（2）打开抽气泵，降低玻璃管内气压p，保持电流I不变，读出电压表示数U，计算出对应的金属丝阻值；

（3）根据测量数据绘制R-p关系图线，如图10（d）所示；

（4）如果玻璃管内气压是0.5个标准大气压，保持电流为100 mA，电压表指针应该在图10（c）指针位置的 侧（填“左”或“右”）；

（5）若电压表是非理想电压表，则金属丝电阻的测量值 真实值（填“大于”“小于”或“等于”）．

【解析】 （1）电压表量程为0-3 V，分度值为0.1 V，则电压表读数需估读一位，读数为1.23 V，根据欧姆定律可知，金属丝的测量值R=UI=12.3 Ω；

（4）据图（d）可知气压越小电阻越大，再根据U=IR可知压强p减小，则电阻R增大，故电压增大，电压表的指针位置应该在题图10（c）中指针位置的右侧；

（5）由欧姆定律U=R测I，因电流表采用外接法会导致电压表分流，即U=R真（I-URV），变形为：U=R真1+R真RVI，两式相比，R测<R真．

【例2】 （2024年新课标Ⅱ卷）某探究小组要测量电池的电动势和内阻．可利用的器材有：电压表、电阻丝、定值电阻（阻值为R0）、金属夹、刻度尺、开关S、导线若干．他们设计了如图11所示的实验电路原理图．

图11

（1）实验步骤如下：

①将电阻丝拉直固定，按照图（a）连接电路，金属夹置于电阻丝的 ．（填“A”或“B”）端；

②闭合开关S，快速滑动金属夹至适当位置并记录电压表示数U，断开开关S，记录金属夹与B端的距离L；

③多次重复步骤②，根据记录的若干组U、L的值，作出图（c）中图线Ⅰ；

④按照图（b）将定值电阻接入电路，多次重复步骤②，再根据记录的若干组U、L的值，作出图（c）中图线Ⅱ．

（2）由图线得出纵轴截距为b，则待测电池的电动势E= ．

（3）由图线求得Ⅰ、Ⅱ的斜率分别为k1、k2，若k2k1=n，则待测电池的内阻r= （用n和R0表示）．

【解析】 （1）为了保护电路，闭合开关前，金属夹置于电阻丝的最大阻值处，由图可知，应该置于A端．

（2）对于电路图（a），根据闭合电路欧姆定律有U=E－Ir，设金属丝的电阻率为ρ，横截面积为S，结合欧姆定律和电阻定律I=UR，R=ρLS，联立可得U=E－USρLr，整理可得1U=1E+SrEρ·1L，对于电路图（b），根据闭合电路欧姆定律有U=E－I（r+R0），结合欧姆定律和电阻定律I=UR，R=ρLS，联立后整理1U=1E+S（r+R0）Eρ·1L，可知图线的纵轴截距b=1E，解得：E=1b．

（3）由题意可知k1=SrEρ，k2=S（r+R0）Eρ，又k2k1=n，联立解得：r=R0n-1．

【点评】 从本题可看出，利用一次函数法不仅可以分析误差，还对实验数据的处理有优势，当然利用闭合电路欧姆定律这个核心规律列方程是解决问题的关键．

六、启示

利用“一次函数法”对主要电学实验进行误差分析是对其他方法的补充，同时能加深学生对数学和物理结合、代数与图形的理解，“一次函数法”除了分析误差，对实验数据的处理也很方便，提倡利用数学方法处理物理问题，进一步促进学生的实验探究科学素养．

【作者简介：特级教师，正高级教师，全国先进工作者，教育部国培计划专家，公开发表论文百余篇，出版专著7本】

责任编辑 李平安