离散数学思维在物流学科中的应用研究

摘 要：随着全球贸易和电子商务的不断扩大，物流需求持续增长。然而，物流行业在处理日益复杂的供应链和物流网络方面面临着专业人才短缺问题。物流行业需要更多高素质的专业人才来满足增长的需求，但供给方面却没有跟上。这一矛盾使得物流人才缺口问题愈发凸显。离散数学在培养物流人才方面扮演着重要的角色，它为物流人才提供了有效的数学工具和方法，提高运作效率和质量，并推动物流行业的发展。因此，文章旨在系统梳理离散数学在物流领域的具体应用，对于制定物流专业培养方案和课程具有重要的参考价值。通过确保学生快速掌握离散数学的核心知识，可以培养更多适应物流行业需求的高素质专业人才，并为物流行业的发展做出贡献。

关键词：物流管理；物流人才；离散数学

中图分类号：F251；G642 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.18.033

Abstract： With the continuous expansion of global trade and e-commerce， logistics demand continues to grow. However， the logistics industry is facing a shortage of professional talents in dealing with increasingly complex supply chains and logistics networks. The logistics industry needs more high-quality professionals to meet the growing demand， but the supply side has not kept up. This contradiction has made the shortage of logistics talents increasingly prominent. Discrete Mathematics plays an important role in cultivating logistics talents. It provides effective mathematical tools and methods for logistics talents， improves operational efficiency and quality， and promotes the development of the logistics industry. Therefore， this article aims to systematically review the specific applications of discrete mathematics in the field of logistics， providing important reference value for the development of logistics professional training programs and courses. By ensuring that students quickly master the core knowledge of discrete mathematics， more high-quality professional talents can be trained to meet the needs of the logistics industry and contribute to the development of the logistics industry.

Key words： logistics management; logistics talent; discrete mathematics

1 背景介绍

随着全球贸易和电子商务的不断扩大，物流需求持续增长。然而，物流行业在处理日益复杂的供应链和物流网络方面面临着专业人才短缺问题。物流行业需要更多高素质的专业人才来满足增长的需求，但供给方面却没有跟上。这一矛盾使得物流人才缺口问题愈发凸显。为适应时代的发展，以培养一大批引领未来技术与产业发展的工科人才和提高我国人才竞争力和吸引力为目的，新工科的教育改革应运而生。在当前的时代背景下，物流管理专业也迎来了新的机遇和挑战。

为了解决这个问题，可以采取教育培训、行业合作和人才引导等措施。通过加强物流专业的教育培训，提供系统化的学习和实践机会，培养更多的物流专业人才。同时，行业合作可以加强学校与企业之间的合作关系，提供实际案例和实践经验，使学生更好地掌握物流领域的知识和技能。现代物流人才不仅应具备扎实的管理学科知识，还要能够掌握计算机、数学等专业知识以分析、解决物流与供应链管理问题，并具有较强的创新能力和较全面的物流专业素养。为此，越来越多的开设物流管理专业的高校，将离散数学、概率论等数学专业课程纳入到物流管理专业的培养方案中[1]。

离散数学是现代数学的一个重要分支。它是以研究离散变量的结构和相互之间的关系为主要目标，研究对象通常是有限个或可数个元素。在物流学科中，离散数学思维可以应用于许多方面，包括网络优化、路径规划、库存管理和调度等。以下是离散数学思维在物流学科中的一些具体应用探究。

图论：图论是离散数学中的一个重要分支，它研究图的性质、结构和算法。在物流学科中，图论可以应用于网络优化和路径规划问题。例如，可以使用最短路径算法（如Dijkstra算法或Floyd-Warshall算法）来确定最佳路径，以最小化货物的运输成本或减少交通拥堵。

组合数学：组合数学研究对象的组合、排列和选择等离散结构。在物流学科中，组合数学可应用于库存管理和订单拣选等问题。例如，可使用组合数学中的排列组合方法来确定最佳仓库布局，以最大化存储空间利用率。

排队论：排队论是研究排队系统的性能和行为的数学分支。在物流学科中，排队论可以应用于仓库和配送中心的调度和运营。通过排队论模型，可以评估不同的调度策略，以最大化物流效率和服务水平。

最优化理论：最优化理论研究如何找到最佳解决方案的数学方法和技术。在物流学科中，最优化理论可以应用于货物配送路径的优化、运输成本的最小化以及资源分配的优化等问题。使用最优化算法（如线性规划、整数规划或动态规划），可以找到最佳的物流决策和方案。

随机过程：随机过程是描述随机事件随时间发展的数学模型。在物流学科中，随机过程可应用于需求预测和库存控制。通过建立概率模型，可以预测未来的需求，并制定相应的库存策略，以确保及时供应并降低库存成本。

总的来说，离散数学思维在物流学科中的应用可以帮助优化物流系统的运作，提高效率，降低成本，并提供决策支持。这些数学方法和技术可以帮助物流专业人员解决复杂的问题，改进物流流程，并为供应链管理提供更好的解决方案。

2 图论在物流中的应用

图论在物流中有广泛的应用，本文以下面几个内容重点阐述图论在物流中的具体应用[2]。

2.1 最短路径算法

最短路径算法是图论中的经典算法，可以在物流中用于确定最短路径，以最小化货物的运输成本或减少交通拥堵。例如，在运输网络中，可以使用Dijkstra算法或Floyd-Warshall算法找到两个地点之间的最短路径，从而确定货物的最佳运输路径。

2.2 网络优化

图论可以应用于物流网络的优化。通过建立一个图模型，将物流网络中的节点表示为仓库、工厂、配送中心等，边表示物流路径或运输线路，可以使用最小生成树算法或其他网络优化算法来寻找最优的物流网络结构，以降低物流成本并提高运输效率。

2.3 资源分配与配送问题

图论可以应用于物流中的资源分配和配送问题。例如，在货物配送中，可以使用图的着色算法来确定最佳的配送路线和车辆调度，以最大化资源利用率并满足时间窗口约束。

2.4 仓库布局优化

图论可以应用于仓库布局的优化。通过将仓库内的货架、货位等表示为图的节点，将路径和距离表示为边，可以使用图论算法来确定最佳的货物存储和拣选路线，以最大化仓库空间利用率和减少物流操作时间。

2.5 配送路径规划

图论可以应用于配送路径规划的优化。通过将配送地点表示为图的节点，将路径和距离表示为边，可以使用图论算法来确定最优的配送路线，以减少行驶距离、节约时间和降低运输成本。

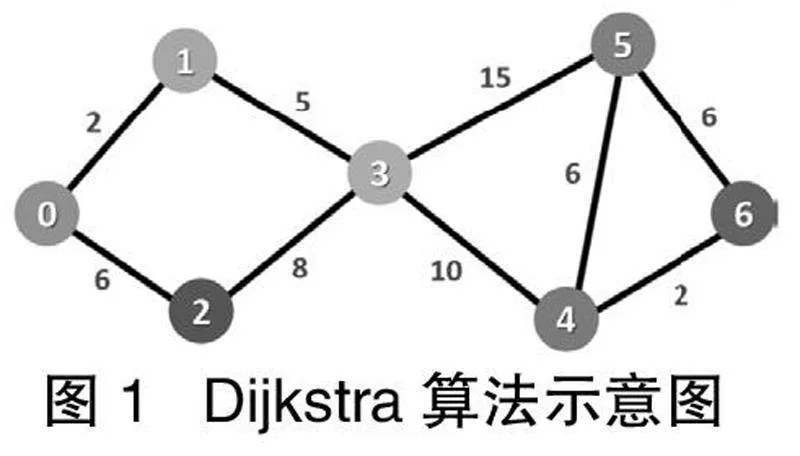
客观上讲，离散数学的教学内容太过于理论化，所涉及到的概念多、符号多、定理多，基本沿用了“定义—定理—证明”的教学模式[3]。在教授这部分知识时可以做到图形并茂，例如当讲授最短路径Dijkstra算法时，可以适当引入一些以物流配送路径规划为背景的问题来讲解，有效提高课程效率。让学生深刻认识到通过应用图论的算法和技术，可以优化物流系统的运作，提高效率，降低成本，并提供更好的决策支持。图1为Dijkstra算法示意图。

3 组合数学在物流中的应用

组合数学在物流中有多个应用领域，以下是一些组合数学在物流中的具体应用[2]。

3.1 排列组合在库存管理中的应用

组合数学中的排列和组合方法可以应用于库存管理中的需求预测和库存优化。通过分析历史数据和不同产品的销售模式，可以使用排列组合方法来确定最佳的库存订货量和补货策略，以最大化库存周转率并减少库存成本。

3.2 集合覆盖算法在订单拣选中的应用

在物流中，订单拣选是一个重要环节，需要有效地选择货物以满足订单需求。集合覆盖算法是组合数学中的一种技术，可以应用于订单拣选的优化。通过将订单与可用货物之间的关系表示为集合，可以使用集合覆盖算法来确定最少的拣选操作，以满足所有订单需求，减少运输时间和人力成本。

3.3 图的着色算法在资源分配中的应用

资源分配是物流中的一个重要问题，涉及将有限的资源（如车辆、人力等）分配给不同的任务或地点。图的着色算法是组合数学中的一种技术，可以应用于资源分配的优化。通过将任务或地点表示为图的节点，并定义资源之间的约束关系，可以使用图的着色算法来确定最佳的资源分配方案，以最大化资源利用率并满足约束条件。

通过应用组合数学的方法和技术，可以优化物流过程，提高效率，并提供更好的决策支持，以确保物流系统的高效运作。

4 排队论在物流中的应用

排队论是研究队列或排队系统的数学理论，它在物流中有多个应用领域。以下是一些排队论在物流中的具体应用[4]。

4.1 排队模型在仓库和配送中心调度中的应用

在物流中，仓库和配送中心常常面临货物进出的排队问题。排队论可以用于建立排队模型，分析和优化货物进出的调度策略。通过考虑排队长度、等待时间和服务时间等因素，可以确定最佳的调度规则，以提高仓库和配送中心的运作效率和服务水平。

4.2 排队论在服务水平评估中的应用

物流中的服务水平评估是一个关键指标，它衡量了物流系统对客户需求的响应能力。排队论可以应用于模拟物流系统中的排队行为，并评估服务水平指标，如平均等待时间、平均排队长度和服务水平达标率。通过排队论的分析，可以识别瓶颈环节并采取相应的措施来改善服务水平。

4.3 排队论在物流网络优化中的应用

物流网络中的运输节点和路线通常存在排队问题。排队论可以应用于物流网络的优化，以最大化资源利用率和降低运输成本。通过建立排队模型，可以确定最佳的运输节点布局、调度策略和路线规划，以优化物流网络的运作效率和服务质量。

4.4 排队论在供应链管理中的应用

供应链中存在着许多环节和节点，涉及物流流程和资源分配。排队论可以应用于供应链中的排队系统分析，以优化供应链的效率和响应能力。通过建立排队模型，可以评估和优化供应链中的等待时间、库存水平和资源利用率等指标，以提高供应链的整体效能。

通过应用排队论的方法和技术，可以改善物流系统的运作，提高服务水平，并优化资源分配，以满足客户需求并降低成本。

5 最优化理论在物流中的应用

最优化理论在物流中有广泛的应用，以下是一些最优化理论在物流中的具体应用[5]。

5.1 线性规划在运输成本最小化中的应用

线性规划是最优化理论的一个重要分支，可以应用于物流中的运输成本最小化问题。通过建立数学模型，将运输成本、供应量、需求量等变量表示为线性关系，可以使用线性规划方法来确定最佳的产品运输方案，以降低运输成本并满足需求。

5.2 整数规划在路径规划和资源分配中的应用[6]

整数规划是一种最优化方法，它在物流中的路径规划和资源分配问题中得到广泛应用。例如，在配送路线规划中，可以使用整数规划来确定最佳的配送路径，以最小化总行驶距离或最大化配送效率。在资源分配中，整数规划可以帮助确定最佳的资源分配方案，如车辆调度、仓库容量分配等。

5.3 动态规划在库存管理和调度中的应用

动态规划是一种最优化方法，可以应用于物流中的库存管理和调度问题。建立状态转移方程和最优化准则，可以使用动态规划来确定最佳的库存补货策略、订单分配策略和调度计划，以最大化库存周转率、减少缺货风险和提高运输效率。

5.4 非线性规划在物流网络优化中的应用

非线性规划是一种在物流网络优化中常用的最优化方法。物流网络中存在着多个非线性的约束条件和目标函数，如运输时间、交通拥堵、资源利用率等。通过建立适当的数学模型，并使用非线性规划方法，可以优化物流网络的结构和运作，提高效率、降低成本，并满足各项约束条件。

应用最优化理论的方法和技术，可以优化物流系统的运作，提高效率，降低成本，并提供更好的决策支持，以确保物流网络的高效运行。

6 随机过程在物流中的应用

随机过程是研究随机事件随时间变化的数学模型，它在物流中有多个应用领域。以下是一些随机过程在物流中的具体应用[7-9]。

6.1 马尔可夫链在库存管理中的应用

马尔可夫链是一种随机过程，可以用于建模库存管理中的需求波动。通过分析历史需求数据和不同产品之间的转移概率，可以建立马尔可夫链模型，预测不同库存水平下的需求情况。这样可以帮助优化库存策略，提高库存周转率，减少过剩库存和缺货风险。

6.2 随机漫步在货物路径选择中的应用

随机漫步是一种随机过程，可以应用于货物路径选择问题。在物流中，货物通常需要从起点到达目的地，而路线上可能存在不确定性因素，如交通拥堵、道路条件等。通过建立随机漫步模型，可以模拟货物在不同路径上的移动，并评估每条路径的风险和效率，以选择最佳路径。

6.3 泊松过程在订单到达模式中的应用

泊松过程是一种常见的随机过程，可以应用于模拟订单到达模式。在物流中，订单的到达通常具有随机性，而订单到达的模式对配送和调度计划具有重要影响。通过建立泊松过程模型，可以模拟订单到达的随机性，并根据模型预测的到达率来优化配送计划和资源分配。

6.4 马尔科夫决策过程在调度和资源分配中的应用

马尔科夫决策过程是一种随机过程，可以用于物流中的调度和资源分配问题。在物流中，需要根据当前状态和随机事件进行决策，如车辆调度、任务分配等。通过建立马尔科夫决策过程模型，可以优化调度和资源分配策略，以最大化系统效率和满足约束条件。

通过应用随机过程的方法和技术，可以更好地理解和处理物流中的不确定性和随机性，优化决策和规划，提高物流系统的效率和鲁棒性。

7 结 语

离散数学思维在物流学科中的应用可以帮助优化物流系统的运作，提高效率，降低成本，并提供决策支持。这些数学方法和技术可以帮助物流专业人员解决复杂的问题，改进物流流程，并为供应链管理提供更好的解决方案。本文系统总结了离散数学在物流行业中的具体应用，旨在提高学生的学习积极性和学习效率，做到有的放矢，重点攻克，快速增强学生利用离散数学理论分析和解决实际物流问题的能力，培养更多物流综合人才。

参考文献：

[1] 周恩毅，于蕊．信息化时代下智慧物流行业人才培养的策略研究[J]．物流科技，2023，46（22）：170-176.

[2] 孔昊．运筹学在物流管理中的应用运输规划问题[J]．运输经理世界，2021（33）：70-72.

[3] 左孝凌，李为鑑，刘永才．离散数学[M]．上海：上海科学技术文献出版社，1983.

[4] 孙荣恒，李建平．排队论基础[M]．北京：科学出版社，2002.

[5] 晋民杰，崇洁．浅谈最优化理论在物流管理中的应用[J]．物流工程与管理，2017，39（2）：35-37.

[6] 何宝民，董文洪，张凤林，等．整数物流网络资源配置路径优化模型与算法[J]．哈尔滨工业大学学报，2008（10）：1677-1680.

[7] 韩兵，蔺宇．随机过程下的生产配送策略对比[J]．工业工程，2014，17（6）：48-53.

[8] 肖谦，赵海燕．基于马尔科夫模型的物流服务市场占有率的预测[J]．湖南社会科学，2014（4）：132-134.

[9] 郁宇卫．随机过程理论在库存管理中的应用——对连续型和离散型（s，Q）模型的求解[J]．物流科技，2009，32（12）：26-29.