基于缓解交通拥堵路况的信号灯配时及道路导向优化研究

摘 要：随着城市化进程的不断推进，交通拥堵问题成为影响城市居民生活和企业运营的主要挑战之一。文章旨在通过优化城市交叉口红绿灯时序，改善城市交通拥堵状况，提高交通流畅性和安全性。红绿灯作为交通控制的关键因素，其时序规划的合理性直接关系到城市交通系统的运行效率。为了应对城市交通的复杂性和多样性，文章构建了一个综合考虑机动车、行人和非机动车等多种交通参与者的微观交通仿真模型，通过数学公式和遗传算法进行优化，旨在找到最佳的红绿灯时序配置，以实现交通系统的最优化。文章的仿真实验选取了城市实际交叉口为案例，通过调整红绿灯时序观察交通流的变化，验证了模型和算法的有效性。通过研究发现，优化红绿灯时序不仅能够改善交通拥堵问题，提高交通流畅性，还能保障行人及非机动车的交通安全，这为未来城市的可持续发展和居民的出行提供了有益的参考和指导。

关键词：红绿灯时序；交通系统；运行效率；仿真实验；可持续发展

中图分类号：F49；U491 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.18.023

Abstract： With the continuous advancement of urbanization， traffic congestion has become one of the main challenges affecting the lives of urban residents and business operations. The aim of this study is to improve urban traffic congestion， traffic smoothness， and safety by optimizing the timing of traffic lights at urban intersections. As a key factor in traffic control， the rationality of the timing planning of traffic lights directly affects the operational efficiency of urban transportation systems. In order to address the complexity and diversity of urban traffic， this paper constructs a micro traffic simulation model that comprehensively considers various traffic participants such as motor vehicles， pedestrians， and non motor vehicles. Through mathematical formulas and genetic algorithms， the model is optimized to find the optimal timing configuration of traffic lights and achieve the optimization of the transportation system. The simulation experiment in this article selected an actual urban intersection as a case study， and verified the effectiveness of the model and algorithm by adjusting the timing of traffic lights to observe changes in traffic flow. Through research， it has been found that optimizing the timing of traffic lights can not only improve traffic congestion and smoothness， but also ensure the safety of pedestrians and non motorized vehicles. This provides useful reference and guidance for the sustainable development of cities and the travel of residents in the future.

Key words： traffic light timing; transportation system; operating efficiency; simulation experiments; sustainable development

0 引 言

随着城市化进程的不断推进，城市交通问题逐渐严峻。交通拥堵、交通事故和环境污染等问题不仅严重影响着居民的出行体验，还对城市的可持续发展提出了挑战。根据中国社会科学院和其他相关机构的研究，交通拥堵对城市经济和社会造成的成本因多种因素而异。这些因素包括城市的规模、交通拥堵的程度、交通管理措施的效果等。具体成本会根据这些因素而有所不同。一般来说，交通拥堵会产生时间浪费、燃料消耗增加、环境污染加剧、交通事故风险增加等，从而对城市的经济和生活质量产生负面影响。这些影响会导致直接和间接的成本。其中直接成本包括交通时间损失、燃料费用增加、运输成本增加等。而间接成本包括环境污染治理费用、医疗费用、交通事故处理费用等。红绿灯作为交通控制的城市道路“指挥官”，对交通的流畅性和安全性起着关键作用。其中包含通过指示红绿灯状态，控制道路上车辆的流动，协调不同方向的交通流量，以防止交通拥堵和事故发生，帮助车辆和行人有序通行，避免交通混乱；它们提供清晰的信号，确保车辆和行人在适当的时候停车和通行，减少了交通冲突和碰撞的机会；它们提供行人过马路的安全时机，可以优化交通流动，减少交通拥堵，提高道路通行效率，这有助于节省时间和燃料成本；同时，也可以降低车辆的怠速时间，从而减少尾气排放和环境污染。因此，寻求一种智能、绿色和低碳的城市交通管理理念变得至关重要。

1 相关研究回顾

1.1 交通信号灯控制系统相关研究

城市交通拥堵已经成为国内外交通管理者和学者的研究焦点，在现有的研究上面，主要分为两个方面，一是交通信号灯控制系统研究方面，张健提出了基于ZigBee在交通信号灯上的应用，在固定配时的基础上，对信号灯配时及机动车道路选择提供方案，可以改善道路的拥堵情况，但该方法适用于宏观调控，不适用于单条或几条道路的调控[1]；赵晓华等将混杂系统理论应用在交通信号灯系统控制上，通过仿真寻找最佳灯色切换时刻和最佳次序，但该算法只局限探究平均排队时长，并没有综合考虑每相位车道不同方向的灯色时间[2]；张迪提出交通信号灯控制的智能算法，即车流量越大，绿灯时间越长的算法以保证交通畅通，但该观点只适用于城市非主干路，对辐射交通网络没有影响[3]；陈汉禄等研究干线协调下行人固定请求的信号灯控制应用，为保证行人安全过街，且对机动车影响较小而设计了请求控制算法并进行仿真，该研究对象主要为行人，并对缓解交通拥堵起显著作用[4]。

1.2 交通信号灯配时相关研究

二是交通信号灯配时研究方面，Wei等通过大量实地调研和仿真实验，采用传统调度方法尝试优化交通，但面对城市交通的复杂性，效果不是十分显著[5]；Loder等提出TRRL配时法，重点考虑车辆延误时间，对红绿灯进行固定配时，但不适用于拥堵路段[6]；李岩等基于NSGA算法研究过饱和状态下的交通信号灯配时，但并未考虑行人及非机动车的安全通行情况[7]；陶超等以降低车辆延误为目标，采用模糊控制理论对交通信号灯的顺序和灯色进行配时调整，并设计算法以弥补模糊控制理论的缺陷，但不能兼顾更多的交通参数[8]；吴妮提出一种车辆拥堵路口自适应信号灯配时的框架，以二氧化碳排放量最低为目标进行优化求解，运用遗传算法，对不同交通情况的路口设计相应的交通信号灯配时方案，但该方法需要多次迭代实验进行动态调整，并不适用于目前城市道路的实际情况[9]。

综上所述，目前国内外学者对交通信号灯的研究对象多为系统控制及配时，鲜有综合考虑四相车道并且每相车道具有不同方向交通信号灯配时的问题，故本文旨在研究考虑多个车道方向，且兼顾行人和非机动车通行问题，合理分配各信号灯配时及次序，以降低交通拥堵，改善城市交通。

2 问题描述

随着城市化进程的不断推进，城市交通拥堵问题逐渐凸显，因此，寻找有效的交通管理手段成为当前城市规划和发展的迫切需求之一。红绿灯作为城市交通控制系统的重要组成部分，直接影响车辆、行人和非机动车在路口的通行效率。合理优化红绿灯时间，不仅可以有效提高交通流畅性，减少拥堵，还有助于增加交通安全性和改善城市交通效率。因此，本研究旨在通过优化红绿灯时间，探索一种可行的方法来改善城市交通拥堵情况。

首先，本文考虑了城市交通系统的复杂性，包括机动车、行人和非机动车等多种交通参与者。在这个多元化的背景下，本文重点关注红绿灯时序规划对不同交通参与者的影响，以及如何通过调整时序来实现交通流畅和交通安全的平衡。然后，综合考虑车辆流量、车道数、行人数量、非机动车数量以及机动车数量等多个因素，构建微观交通仿真模型，并考虑不同车辆的通行速度、流量等动态因素。最后进行算法设计及仿真实验。

因此，本文的问题可描述为：针对某个车流量较大的交通路口，在一个红绿灯时间周期之内（从某一个方向的红灯刚熄灭，绿灯刚亮起的瞬间开始计时，期间所有红绿灯均经历绿灯亮起、红灯亮起的过程，直到计时的第一个绿灯再次亮起时为一个交通周期），已知该路口在整个交通周期的机动车数量、非机动车数量及行人数量、车辆及行人行驶最低速度和平均速度、车道数量及方向等相关信息，以单个交通周期内保证绝大多数的车辆及行人均能通过路口的前提下，交通时间周期最短、各路口红绿灯时间安排合理为目标函数，建立微观交通仿真模型，最终给出为保证各个路口的车辆通过率，各个方向指示绿灯时间安排及道路指向的规划。

3 数学模型

3.1 模型假设

本文在主干路交通信号灯调控优化的过程中，由于单个路口的交通情况所产生的影响会辐射一片区域，甚至整个交通网络，故本文作出如下假设。

第一，模型所优化的交通信号灯只对该路口的交通情况产生主要影响，因控制整个交通周期总长波动较小，所以不考虑对周边辐射区域的影响；

第二，模型中机动车辆、非机动车辆、行人反应及速度基本保持一致；

第三，模型中不考虑特殊情况，例如肇事、车辆抛锚等影响交通的情况；

第四，所有车辆、行人均遵守交通信号灯指挥通行。

3.2 符号参数

3.3 模型构建

3.3.1 目标函数

其中，目标函数是最小化车辆、行人和非机动车的通行时间，同时确保绝大多数车辆可以在保证安全的前提下通过路口；代表机动车辆的通行时间；代表行人的通行时间；代表非机动车的通行时间。

3.3.2 约束条件

其中，式（2）表示交通周期约束，即所有车道的周期时间之和不应超过交通周期；式（3）表示绿灯时间足够长的约束：确保每个车道的绿灯时间足够长，以满足机动车的通行时间，同时不浪费时间，确保行人和非机动车有足够的时间通行，缓解交通压力。其中，是每个车道的最小绿灯时间，以确保行人和非机动车有足够的时间来通行；式（4）为交通流量平衡：确保每个车道上的车辆流量在合理范围内；式（5）为交通安全约束：考虑交通安全，确保通行时间不会导致交通事故。添加约束，限制车道上的通行速度。是每个车道上的最大允许速度，以确保安全通行；式（6）为通行时间差异约束：考虑不同车道上车辆通行时间的差异，约束以限制通行时间差异。和分别表示车道上通行时间的最大值和最小值，是允许的通行时间差异；式（7）为红绿灯协调约束：确保机动车、行人和非机动车的绿灯时间协调，以避免通行冲突；式（8）为行人和非机动车绿灯时间约束：当红灯亮起时，行人和机动车绿灯时间应足够长，以确保行人通行。

4 算法设计

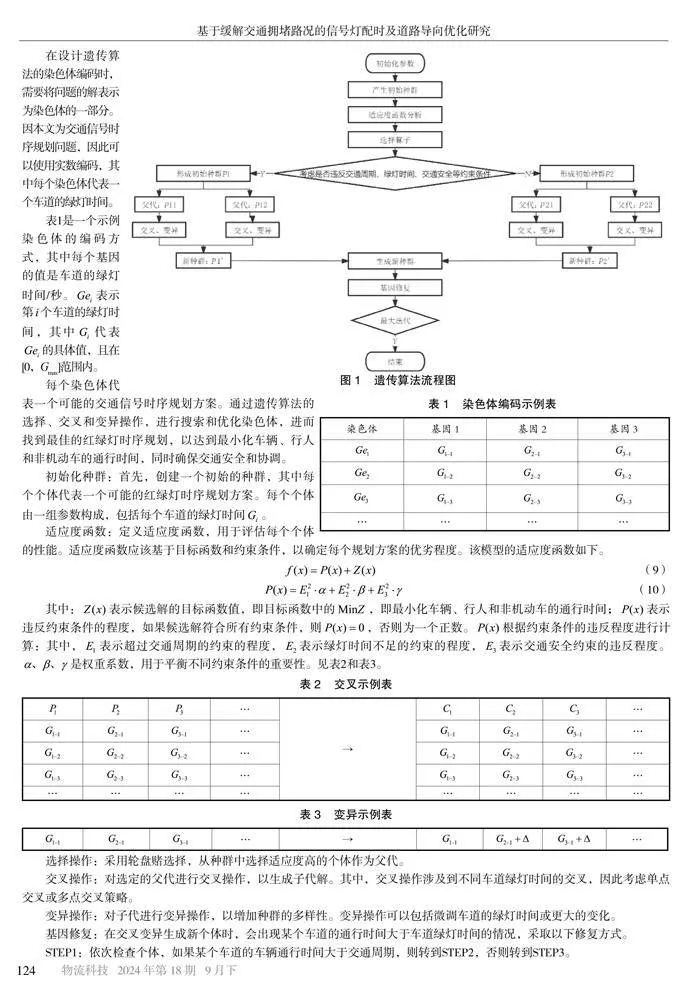
本文的数学模型为混合整数线性规划模型，考虑到本文计算量较大，依据模型的特点，设计了改进遗传算法，通过考虑违反交通周期、绿灯通行时间、交通安全等约束条件的程度形成新种群，再进行交叉变异，最后得出结果，具体流程见图1。

在设计遗传算法的染色体编码时，需要将问题的解表示为染色体的一部分。因本文为交通信号时序规划问题，因此可以使用实数编码，其中每个染色体代表一个车道的绿灯时间。

表1是一个示例染色体的编码方式，其中每个基因的值是车道的绿灯时间/秒。表示第个车道的绿灯时间，其中代表的具体值，且在[0，Gmax]范围内。

每个染色体代表一个可能的交通信号时序规划方案。通过遗传算法的选择、交叉和变异操作，进行搜索和优化染色体，进而找到最佳的红绿灯时序规划，以达到最小化车辆、行人和非机动车的通行时间，同时确保交通安全和协调。

初始化种群：首先，创建一个初始的种群，其中每个个体代表一个可能的红绿灯时序规划方案。每个个体由一组参数构成，包括每个车道的绿灯时间。

适应度函数：定义适应度函数，用于评估每个个体的性能。适应度函数应该基于目标函数和约束条件，以确定每个规划方案的优劣程度。该模型的适应度函数如下。

其中：表示候选解的目标函数值，即目标函数中的，即最小化车辆、行人和非机动车的通行时间；表示违反约束条件的程度，如果候选解符合所有约束条件，则，否则为一个正数。根据约束条件的违反程度进行计算：其中，表示超过交通周期的约束的程度，表示绿灯时间不足的约束的程度，表示交通安全约束的违反程度。是权重系数，用于平衡不同约束条件的重要性。见表2和表3。

在实施这个改进的遗传算法时，应设置合适的参数，以确保算法能够有效地搜索解空间，进而找到最佳的红绿灯时序规划方案，以实现交通流的优化和缓解城市交通压力。

5 仿真模型

5.1 微观交通仿真模型设计

依据模型及算法的特点，本文采用微观交通仿真模型[11]，微观交通仿真模型是一种用于模拟城市道路交通中各种交通参与者（如车辆、行人、自行车等）的行为和互动的复杂计算模型。它模拟交通系统中每个个体的行动，以便更好地了解交通流量、拥堵、事故等情况，用于优化交通控制策略和基础设施规划。微观交通仿真模型通常使用计算机程序来实现[12]，以模拟大规模的交通网络并分析不同情景下的交通表现。这些模型对于城市规划师、交通工程师和交通管理部门来说是强大的工具，可以帮助他们制定更有效的交通控制策略，提高道路安全性，减少拥堵，提高交通效率，以满足不断增长的城市交通需求。

以下是一些微观交通仿真模型所使用的关键元素和原理[13]。

车辆模型：微观交通仿真模型通常包括车辆模型，模拟车辆的运动和驾驶行为。这些模型考虑了车辆的加速、减速、换道、速度限制等因素，以模拟车辆在道路上的行驶。

行人模型：如果仿真模型考虑了行人的影响，它还会包括行人模型，模拟行人的行走行为和交叉路口的穿越。行人模型通常涉及行人的速度、密度、目标位置和行走路径选择等因素。

信号控制模型：微观交通仿真模型通常还包括信号控制模型，模拟红绿灯和交通信号的运作。这些模型决定交通信号何时变化，以及每个方向的绿灯和红灯的时间。

道路网络模型：道路网络模型用于表示城市道路网络的拓扑结构和连接关系。这有助于确定车辆和行人的路径选择以及模拟道路容量和拥堵情况。

交互行为：微观交通仿真模型考虑了交通参与者之间的相互作用。这包括车辆之间的交互、车辆与行人之间的交互，以及交通信号与交通参与者之间的交互。这有助于模拟复杂的交通场景，如拥堵、事故等。

数据输入：仿真模型需要大量的输入数据，如道路属性、交通流量、速度限制、事故数据等。这些数据用于初始化模型和进行仿真实验。

输出和评估：模型输出包括模拟交通流量、拥堵情况、行程时间、事故概率等信息。这些输出用于评估不同策略的效果，优化交通控制和基础设施规划。

5.2 仿真流程

STEP1：数据收集和预处理。仿真的第一步是收集所需的数据，包括道路网络信息、交通流量数据、速度限制、信号控制信息等。这些数据通常来自交通监测设备、地理信息系统（GIS）、历史交通数据等。数据预处理包括清理和格式化数据以供仿真使用。

STEP2：模型构建。根据收集到的数据，构建微观交通仿真模型，包括道路网络、车辆模型、行人模型、信号控制模型等。这些模型用于模拟交通参与者的行为和道路网络的拓扑结构。

STEP3：仿真实验设计。在仿真实验之前，需要明确研究的目标和问题。确定实验的输入参数，如交通流量、信号时序、道路容量等，以及模拟的时间段和区域。

STEP4：仿真运行。利用仿真工具运行模型，模拟交通参与者的行为和道路交通的演变。模拟运行的时间可以是分钟、小时，甚至是一天的交通情景，具体取决于研究的范围和问题。

STEP5：数据分析。在仿真运行完成后，收集和分析输出数据。这包括交通流量、拥堵情况、行程时间、事故率等信息。分析结果用于评估不同策略和情景的效果。

STEP6：策略优化。基于仿真结果，可以进行策略优化，如调整信号时序、道路规划、交通管理策略等，以改善交通效率、安全性和流畅性。

STEP7：报告和决策支持。最终的仿真结果和优化策略可以用于报告编制和决策支持。城市规划师、交通工程师和交通管理部门可以根据仿真结果来制定政策和规划基础设施。

依据本文模型特点及算法流程，具体仿真操作如图2所示。

建立道路网络：定义道路网络，包括道路段的长度、车道数、速度限制等信息。这可以用矩阵或数据结构来表示。

生成车辆：在道路网络上生成一定数量的车辆，并为它们分配起始位置、目标位置、初始速度等信息。

模拟车辆行为：对每辆车辆进行模拟，包括车辆的加速、减速、换道等行为。可以使用车辆动力学模型（如加速度-速度模型）来描述车辆的行为。

模拟交通信号：如果有交通信号控制，需要模拟信号的变化，以决定交叉路口的车辆通行权。

时间步进：模拟运行的时间步进，逐步更新车辆的位置和速度，同时考虑交通信号的变化。

数据记录：记录仿真期间的各种数据，如车辆位置、速度、行程时间等。

可视化和分析：利用MATLAB的可视化工具和数据分析功能，绘制交通流量、拥堵情况等图表，以分析仿真结果。

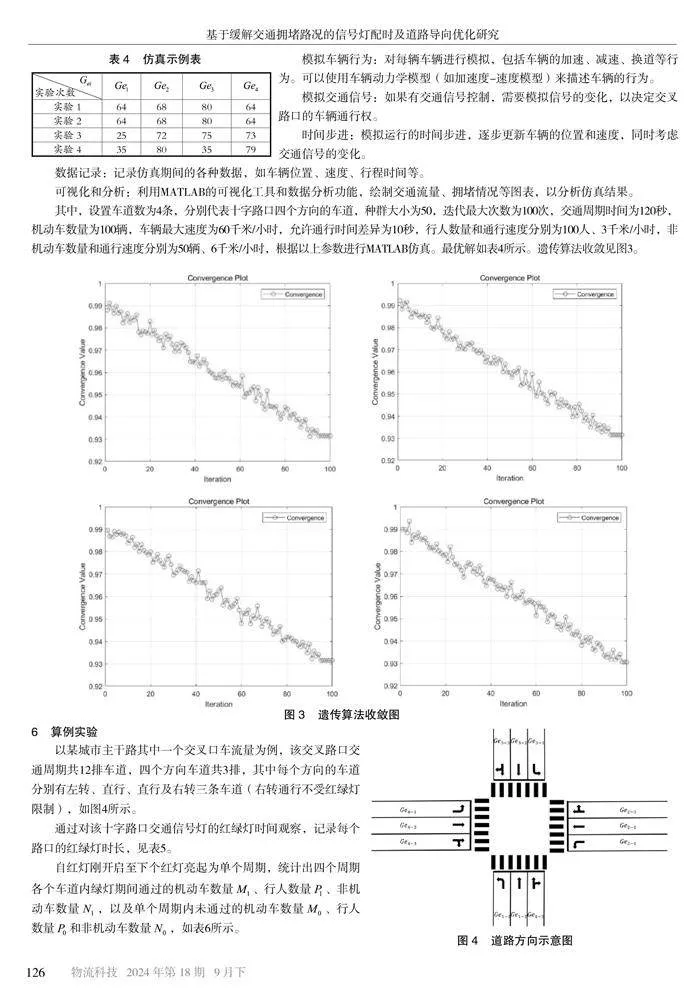
其中，设置车道数为4条，分别代表十字路口四个方向的车道，种群大小为50，迭代最大次数为100次，交通周期时间为120秒，机动车数量为100辆，车辆最大速度为60千米/小时，允许通行时间差异为10秒，行人数量和通行速度分别为100人、3千米/小时，非机动车数量和通行速度分别为50辆、6千米/小时，根据以上参数进行MATLAB仿真。最优解如表4所示。遗传算法收敛见图3。

6 算例实验

以某城市主干路其中一个交叉口车流量为例，该交叉路口交通周期共12排车道，四个方向车道共3排，其中每个方向的车道分别有左转、直行、直行及右转三条车道（右转通行不受红绿灯限制），如图4所示。

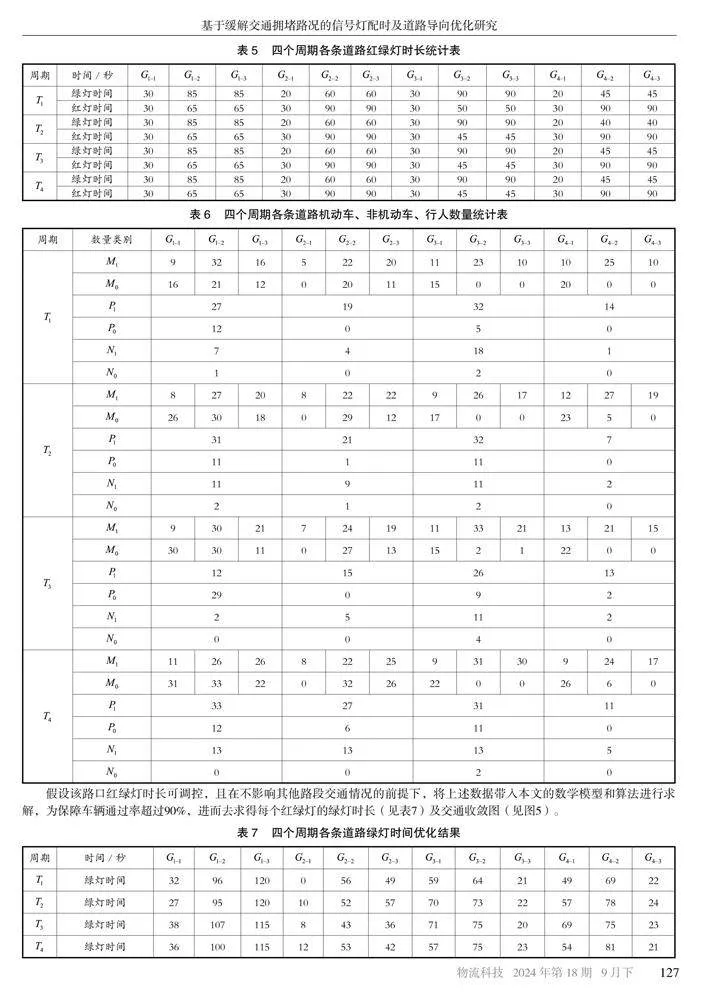
通过对该十字路口交通信号灯的红绿灯时间观察，记录每个路口的红绿灯时长，见表5。

自红灯刚开启至下个红灯亮起为单个周期，统计出四个周期各个车道内绿灯期间通过的机动车数量、行人数量、非机动车数量，以及单个周期内未通过的机动车数量、行人数量和非机动车数量，如表6所示。

假设该路口红绿灯时长可调控，且在不影响其他路段交通情况的前提下，将上述数据带入本文的数学模型和算法进行求解，为保障车辆通过率超过90%，进而去求得每个红绿灯的绿灯时长（见表7）及交通收敛图（见图5）。

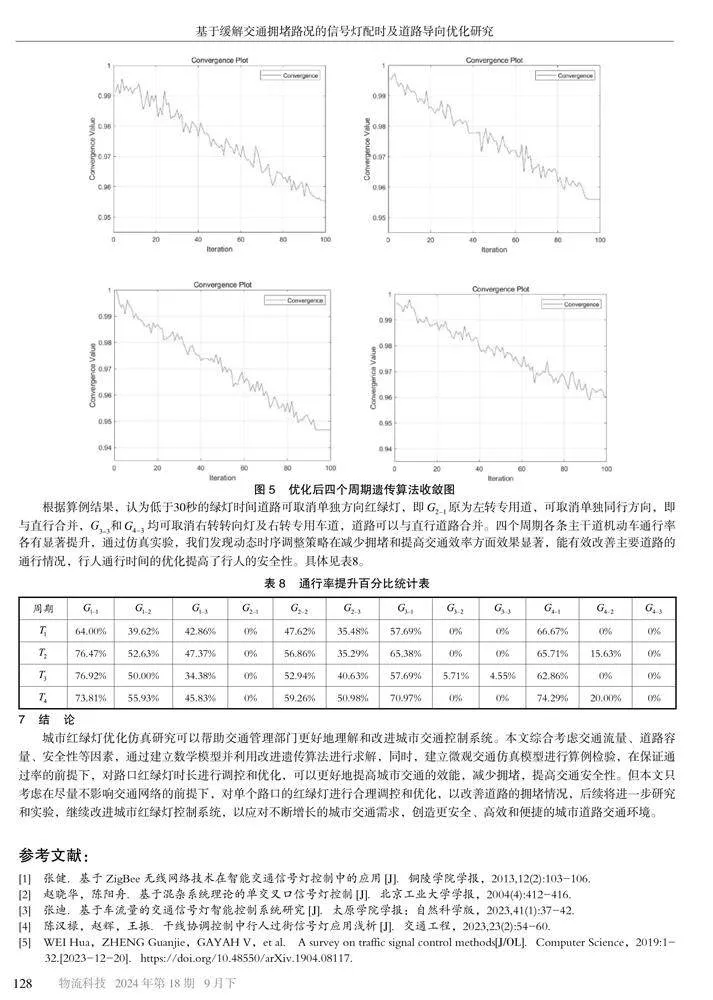
根据算例结果，认为低于30秒的绿灯时间道路可取消单独方向红绿灯，即原为左转专用道，可取消单独同行方向，即与直行合并，G3-3和均可取消右转转向灯及右转专用车道，道路可以与直行道路合并。四个周期各条主干道机动车通行率各有显著提升，通过仿真实验，我们发现动态时序调整策略在减少拥堵和提高交通效率方面效果显著，能有效改善主要道路的通行情况，行人通行时间的优化提高了行人的安全性。具体见表8。

7 结 论

城市红绿灯优化仿真研究可以帮助交通管理部门更好地理解和改进城市交通控制系统。本文综合考虑交通流量、道路容量、安全性等因素，通过建立数学模型并利用改进遗传算法进行求解，同时，建立微观交通仿真模型进行算例检验，在保证通过率的前提下，对路口红绿灯时长进行调控和优化，可以更好地提高城市交通的效能，减少拥堵，提高交通安全性。但本文只考虑在尽量不影响交通网络的前提下，对单个路口的红绿灯进行合理调控和优化，以改善道路的拥堵情况，后续将进一步研究和实验，继续改进城市红绿灯控制系统，以应对不断增长的城市交通需求，创造更安全、高效和便捷的城市道路交通环境。

参考文献：

[1] 张健．基于ZigBee无线网络技术在智能交通信号灯控制中的应用[J]．铜陵学院学报，2013，12（2）：103-106.

[2] 赵晓华，陈阳舟．基于混杂系统理论的单交叉口信号灯控制[J]．北京工业大学学报，2004（4）：412-416.

[3] 张迪．基于车流量的交通信号灯智能控制系统研究[J]．太原学院学报：自然科学版，2023，41（1）：37-42.

[4] 陈汉禄，赵辉，王振．干线协调控制中行人过街信号灯应用浅析[J]．交通工程，2023，23（2）：54-60.

[5] WEI Hua，ZHENG Guanjie，GAYAH V，et al． A survey on traffic signal control methods[J/OL]．Computer Science，2019：1-32.[2023-12-20]．https：//doi.org/10.48550/arXiv.1904.08117.

[6] LODER A，AMBÜHL L，MENENDEZ M，et al．Understanding traffic capacity of urban networks[J/OL]．Scientific reports，2019，9（1）：16283.[2023-11-25]．https：//doi.org/10.1038/s41598-019-51539-5.

[7] 李岩，过秀成，陶思然，等．基于NSGA-Ⅱ算法的过饱和状态交叉口群交通信号配时优化[J]．东南大学学报（英文版），2013，29（2）：211-216.

[8] 陶超，李超，赵骞，等．基于模糊控制的城市单交叉口信号灯配时优化[J]．湖州师范学院学报，2016，38（2）：19-23.

[9] 吴妮．城市过饱和路口信号配时方法研究[D]．武汉：华中师范大学，2018.

[10] 任年鲁，袁逸萍，戴毅，等．基于改进遗传算法的环形RGV系统调度优化[J]．机械设计与制造，2023（4）：1-5.

[11] ABK K，FUJII H，YOSHIMURA S．Efficient origin-destination estimation using microscopictraffic simulation with restrictedrerouting[J]. Computer Modeling in Engineering & Sciences，2023，135（2）：1091-1109.

[12] CAPEK K，KOSONEN I，LUTTINEN R T．Sink&source – An approach for real-time corrections of an online microcopictraffic simulation[C]//13th World Congress and Exhibition on Intelligent Transport Systems（ITS） and Services．London，UK，8-12 October，2006.

[13] BARCELO J，CASAS J．Heuristic dynamic assignment based on microscopic traffic simulation[J/OL]．Computer Science，Engineering，1964（1）：1-12.[2024-11-25]．https：//api.semanticscholar.org/CorpusID：199409591.