AGV“货到人”拣选系统的移动货架选择方法

摘 要：基于自动导引车（AGV）的“货到人”拣选系统，各品类商品可以拆零存放在不同货架上，同一货架也可以存储多种商品，货架的位置也是随机移动的。面对待拣选的订单，选择哪些货架移动到拣选台，以满足订单的品类和数量要求，并最小化选取移动货架个数，是此类型仓库需要解决的关键问题。针对该问题，文章提出基于订单相似度进行订单分批，再通过线性递减权重的粒子群算法来优化移动货架选择解。由于移动货架的优化问题是NP-hard问题，线性规划求解器难以求解，实验结果表明，与线性规划求解器Lingo相比，文本的两阶段移动货架选择方法是有效的，可以在短时间得出求解方案，大大提升了求解效率。敏感性分析进一步揭示了批次数量、品类数量、货架数量以及订单数量，对搬运货架次数的影响，为管理者提供了决策依据。

关键词：“货到人”拣选；自动导引车（AGV）；移动货架；订单相似度；粒子群算法

中图分类号：F252；U492 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.18.007

Abstract： In automated guided vehicle（AGV） "parts-to-picker" picking system， each kind of products can be disassembled and stored in a number of movable racks. A rack can also store multiple products， and the positions of the racks are also randomly moved. For a batch of orders to be picked， it is a key problem that needs to be solved in the application of this new warehousing system to determine which racks should be moved to the picking platform to meet the picking requirements of product types and quantities and minimize the number of the racks to be moved. This paper proposes an order similarity measure method for order batching， and then optimizes the mobile rack selection solution through particle swarm optimization algorithm with linear decreasing weights. Because the optimization problem of the mobile rack is an NP hard problem， it is difficult for linear programming solvers to solve. The experimental results show that， compared with the linear programming solver Lingo， the two-stage mobile rack selection method proposed in this paper is effective and can obtain a solution in a short time， greatly improving the efficiency of the solution. Sensitivity analyses further reveal the influence of batch quantity， category quantity， rack quantity， and order quantity on number of times of rack handling， and provide the important basis of decision for managers.

Key words： "parts-to-picker" picking; automated guided vehicle（AGV）; mobile rack; similarity of orders; particle swarm optimization algorithm

电子商务的发展省去了很多中间环节，很多制造企业将产品库存交由协同发展的第三方物流企业托管，面对高频次、小批量和多品种特征的客户订单，第三方物流企业倾向于通过一个集仓储管理、订单处理、分拣派送于一体的物流配送中心，来适应制造企业的出货要求，实现与制造业在销售环节的联动发展。订单分拣是一个配送中心的核心，直接影响着整个仓库的效率，拣选作业成本占总运营成本的55%以上[1]，选择一种合理有效的拣选策略，在优化分拣作业流程、减少作业处理时间上起到关键作用。

拣选场景一般分为“人到货”拣选和“货到人”拣选。传统“人到货”拣选策略研究比较成熟，构建的模型通常以拣选人员的行走距离或行走时间为优化目标[2-6]，主要将不同的订单相似准则作为约束考虑，例如相同的通道数[7-8]、商品存储位置相近[9]等。“货到人”拣选根据不同的拣选设备，则有miniload“货到人”系统、穿梭车“货到人”系统、AGV“货到人”系统，本文在AGV机器人系统的环境下考虑这一过程，该系统由JÜnemann[10]提出概念，亚马逊首先将其著名的KIVA系统付诸实践[11]。如今，越来越多的类似机器人系统被用于支持现代仓库，例如Swisslog公司的CarryPick™ [12]。

本文研究自动导引车（AGV）“货到人”系统的拣选策略问题，它的优化目标及约束因素与传统“人到货”拣选问题有本质区别，目前基于AGV的“货到人”拣选研究明显少于其在实践中的应用[13]，部分学者对此展开了初步探索。Xiang等[14]研究了基于KIVA系统的存储分配问题，旨在决定将哪个产品放入哪个移动货架，以最大限度地提高产品相似性。Roy等[15]研究了存储区域的AGV机器人分配策略。Yang等[16]研究了基于AGV的拣选系统中订单排序和货架调度的联合优化问题，建立了一个混合整数线性规划模型，并提出了一个两阶段求解过程。Boysen等[17]研究了分拣订单分批和排序，以及被拖到分拣站点的货架排序问题。秦馨等[18]以总搬运货物次数最少为目标，建立了订单分批数学模型，并用遗传算法求解。李珍萍等[19]分析了影响订单拣选成本和效率的两种主要因素，建立了以订单分批拣选总部极小化为目标的整数规划模型，设计了K-MAX聚类算法求解。张国维等[20]以极小化货架搬运成本和商品拣选成本为目标，建立了AGV智能仓库订单分批整数规划模型，并提出了一种基于订单和货架交替选择的贪婪求解算法。李昆鹏等[21]以人工拣选成本和AGV搬运成本之和最小为目标函数构建数学模型，并设计改进自适应遗传算法求解。这些文献提及了货架选择的重要性，但是侧重点是针对订单分批问题建立模型和求解方法，并未给出具体货架的选择方法。

综上研究，本文认为求解AGV“货到人”系统的AGV搬运次数最小化问题，需要解决两个问题，一是决定哪些订单形成同一个批次，二是每一个批次需要搬动哪些货架。本文第一阶段使用订单相似度来进行订单分批，第二阶段使用线性递减权重粒子群算法来改进货架搬运次数解，以探索AGV“货到人”拣选系统移动货架的选择方法。

1 问题描述与模型构建

1.1 问题描述

以AGV为搬运工具的分拣仓中，有货架个，每个拣选台可以容纳个周转箱，整个仓库一共存储个品类的商品，在单位时间内有个订单待拣选，如何将这些订单进行分批拣选。由于此类拣选仓的货架存放位置不是固定的，可以将货物的搬运距离与货物的搬运次数近似看作线性相关，所以只要货架被搬运的次数越少，搬运的总距离或总成本就越低，拣选台的工作效率就越高。基于此，本文以最小化AGV搬运货架次数为目标，决策订单的分配批次以及货架对于订单的服务关系，最终得到合理的订单分批和货架调度方案。

为了方便建立模型，考虑如下假设：所有订单拣选信息在分批前已知；所有货架上的存储商品信息在分批前已知；每个货架有多个货格，每个货格只能存放一个商品，但同一个商品可以在不同的货架中存放；货架上的货物数量大于订单需要的商品数量；订单不允许被分割，每个订单只能被划分到一个批次中；拣选人员拣选不同商品的成本相同；1个周转箱对应1个订单，批次的最大订单数小于等于周转箱数。

1.1aLPOUmda9N0itgLWaXugw==2 模型建立

根据问题描述，符号及变量定义如表1所示。

目标函数（1）表示最小化AGV搬运货架的次数；式（2）表示每个订单只能被分配到一个批次中；式（3）表示一个批次所有订单数量之和小于等于周转箱数；式（4）表示同一批次订单的商品数量之和小于货架上同种类商品数量之和；式（5）和式（6）表示0—1变量。

2 基于订单相似度的订单分批

订单一般包含了物品品类、物品数量、交货地址及日期等诸多信息，订单相似度就是指订单包含的物品品类、交货期等方面具有相似性[22]，通过计算订单相似度，可以减少重复拣选的次数，缩短拣选时间，实现相似度高的订单批量拣选。本文综合考虑订单品类相似度和订单交货期相似度来构建订单相似度，并据此形成初始订单分批方案。品类相似度如下。

表示任意两个订单和之间的品类相似度，其中是订单包含的品类编号，是订单包含的品类编号，是订单和订单具有的相同品类数量，是订单和订单合并后所有品类数量。交货期相似度如下。

表示任意两个订单和之间的交货期相似度，其中是订单的交货期，是订单的交货期，越小，说明两个订单的交货期越接近， 相似度越大，表示订单集D 中两个订单交货期之差的最大绝对值，用于进行归一化处理。最终订单相似度定义如下。

以分别表示品类相似度和交货期相似度的权重。若说明拣选单的构成更注重拣选效率，通过相同品类来减少AGV搬运次数。若，说明拣选单的构成更注重减少订单延迟时间。通过将品类相似度和交货期相似度相结合并赋予不同的权重系数来构建订单相似度进行订单分批，可以达到效率和客户服务水平的平衡，并与最终货架选择结果紧密相关。

3 基于线性递减权重的粒子群货架求解算法

面向批次订单，究竟选择哪些货架移动到拣选台，以满足订单商品品类及数量要求，并最小化货架个数，同样是NP-hard难题，本文设计线性递减权重粒子群算法来求解货架组合，算法步骤如下。

步骤1：根据货架品类和拣选单品类的包含关系，随机初始化货架种群中每个粒子的位置和速度。

步骤2：计算每个粒子的搬运货架次数的适应度值，将粒子的位置和适应度值存储在粒子的个体极值中，将所有个体极值中最优适应度值的个体位置和适应度值保存在全局极值中。

步骤3：更新粒子的位移和速度。代表更新前的货架解粒子，代表更新后的货架解粒子，代表更新前的速度，代表更新后的速度，为惯性权重，c1、c2代表加速度数，r1、r2代表在[0，1]之间随机产生的加速度权重系数。

步骤4：线性递减权重，表示惯性权重最大值，示惯性权重最小值，表示当前迭代步数。

步骤5：对每个粒子，用它的适应度值和个体极值进行比较，如果，则用替换掉。

步骤6：对每个粒子，用它的适应度值和全局极值，比较，如果，则用替换掉。

步骤7：满足最大循环次数，则退出，否则返回步骤3。

4 仿真实验与算法有效性

通过设计仿真实验，利用MATLAB编制程序，对本文提出的基于线性递减权重的粒子群移动货架选择优化算法进行分析，仿真环境为MATLAB 2016a、Window10操作系统、Intel i5-5200U CPU 2.20GHz、16G RAM。本文考虑订单需求多样化、商品库存多货架分布的特点随机生成数据，对6组不同规模的算例进行测试，其中每个货架有4个货格，周转箱数量为3。结果如表2所示，以AGV搬运货架次数为衡量指标。

结果表明，在不同算例规模下，基于订单相似度的货架选择粒子群算法最优解与LINGO计算的最优解没有差别，说明算法的合理性和有效性。在求解时间上，随着订单数和货架数不断增加时，LINGO求解时间耗时较长，而AGV智能仓库对拣选时间要求很高，而本文算法能够在短时间内获得AGV搬运货架次数较少的订单分批方案，具有实用性。

5 敏感性分析

在不同的时间段，顾客订单数量及其订单的商品结构会有很大的不同，例如在电商大促日，顾客的订单数量会激增，每个订单所包含品类也会增多，不同的订单数量、订单品类结构如何影响货架搬运次数，物流仓储方应该如何调整货架数量以及拣选批次，都是需要考虑的问题。本节主要分析批次数量、品类数量、货架数量以及订单数量，对搬运货架次数的影响，旨在给仓储管理者提供相应的管理启示。

5.1 批次数量敏感性分析

算例规模设置订单数为100，货架数为30，每个货架有4个货位，品类数为70，批次数为1、2、4、5、10、20、25、50、100的情况下，测试不同批次数量对AGV搬运货架次数的影响，测试数据随机产生，测试结果取每次测试运行十次中的最小值，再取十次测试的平均值，数据如表3所示。

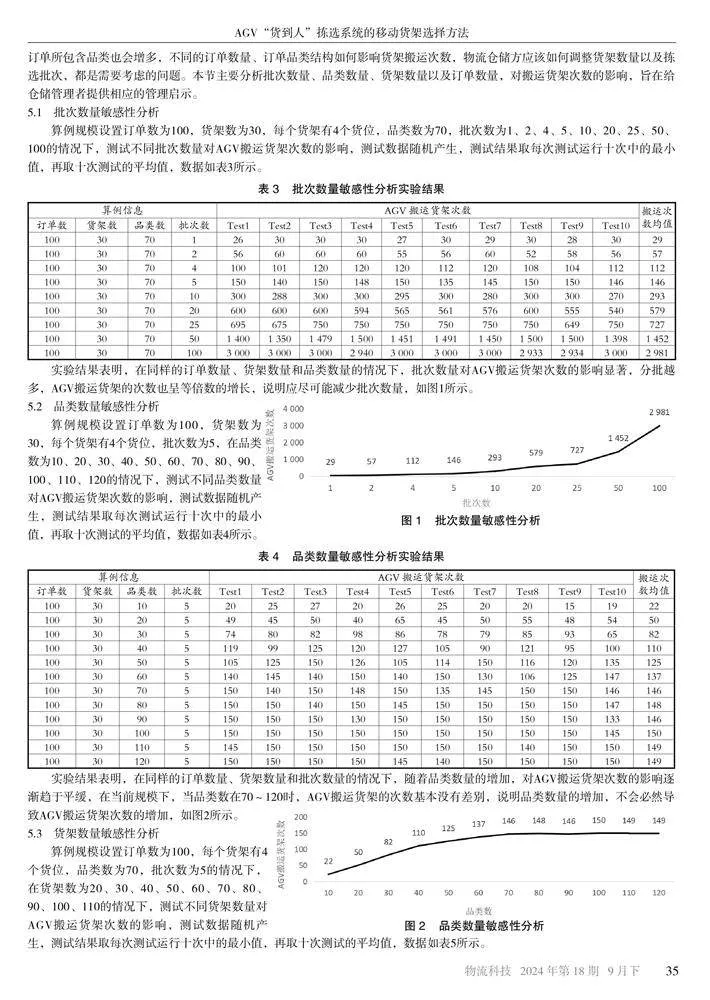
实验结果表明，在同样的订单数量、货架数量和品类数量的情况下，批次数量对AGV搬运货架次数的影响显著，分批越多，AGV搬运货架的次数也呈等倍数的增长，说明应尽可能减少批次数量，如图1所示。

5.2 品类数量敏感性分析

算例规模设置订单数为100，货架数为30，每个货架有4个货位，批次数为5，在品类数为10、20、30、40、50、60、70、80、90、100、110、120的情况下，测试不同品类数量对AGV搬运货架次数的影响，测试数据随机产生，测试结果取每次测试运行十次中的最小值，再取十次测试的平均值，数据如表4所示。

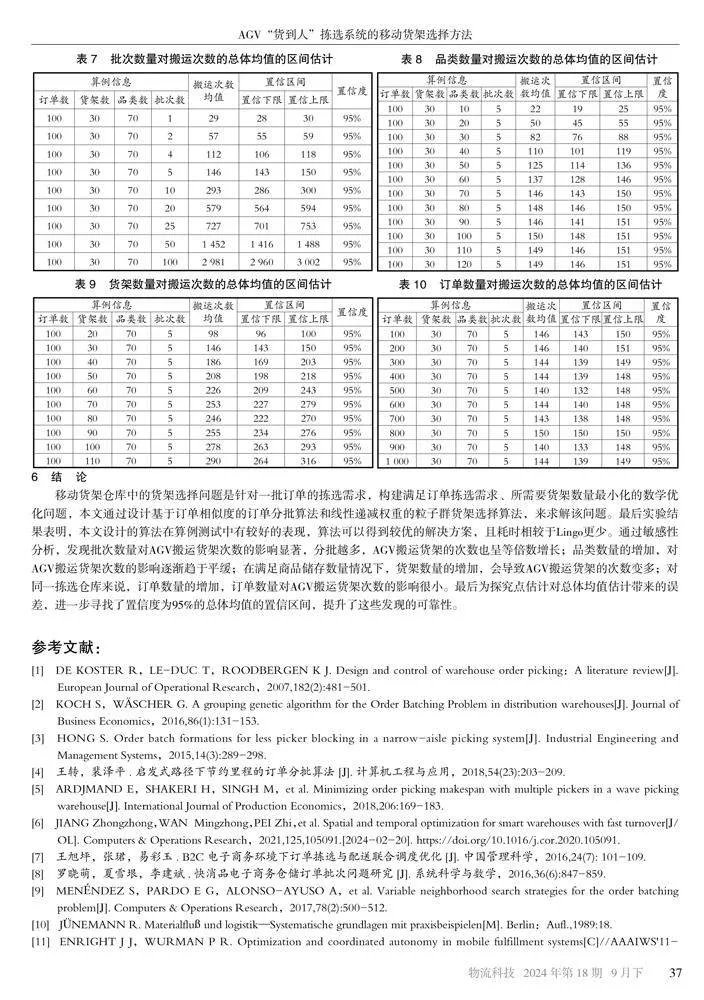
实验结果表明，在同样的订单数量、货架数量和批次数量的情况下，随着品类数量的增加，对AGV搬运货架次数的影响逐渐趋于平缓，在当前规模下，当品类数在70～120时，AGV搬运货架的次数基本没有差别，说明品类数量的增加，不会必然导致AGV搬运货架次数的增加，如图2所示。

5.3 货架数量敏感性分析

算例规模设置订单数为100，每个货架有4个货位，品类数为70，批次数为5的情况下，在货架数为20、30、40、50、60、70、80、90、100、110的情况下，测试不同货架数量对AGV搬运货架次数的影响，测试数据随机产生，测试结果取每次测试运行十次中的最小值，再取十次测试的平均值，数据如表5所示。

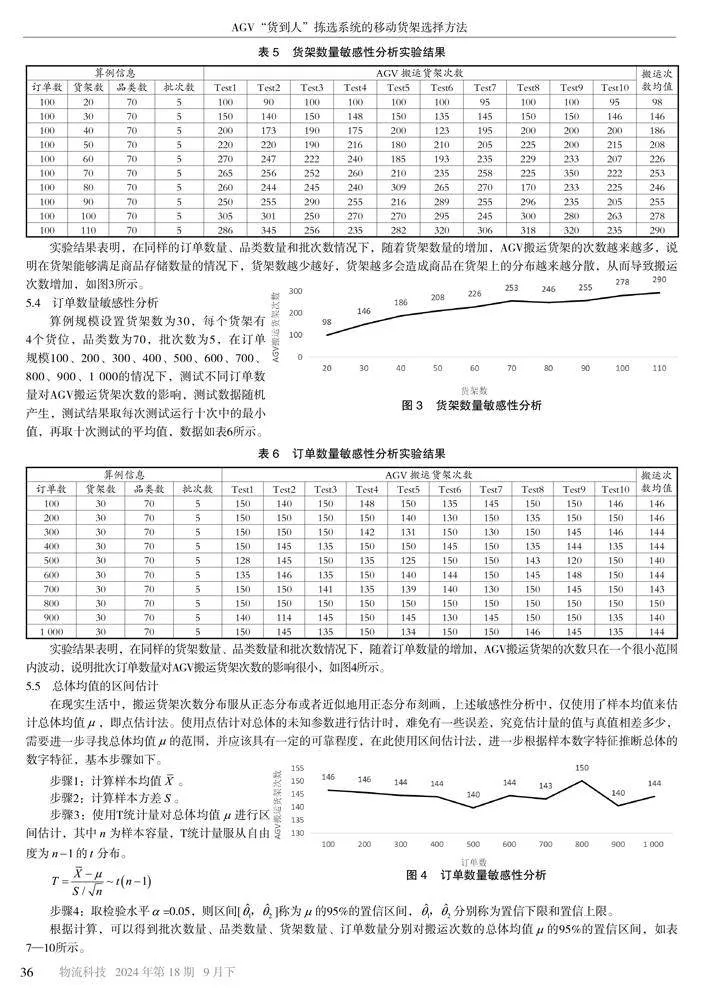
实验结果表明，在同样的订单数量、品类数量和批次数情况下，随着货架数量的增加，AGV搬运货架的次数越来越多，说明在货架能够满足商品存储数量的情况下，货架数越少越好，货架越多会造成商品在货架上的分布越来越分散，从而导致搬运次数增加，如图3所示。

5.4 订单数量敏感性分析

算例规模设置货架数为30，每个货架有4个货位，品类数为70，批次数为5，在订单规模100、200、300、400、500、600、700、800、900、1 000的情况下，测试不同订单数量对AGV搬运货架次数的影响，测试数据随机产生，测试结果取每次测试运行十次中的最小值，再取十次测试的平均值，数据如表6所示。

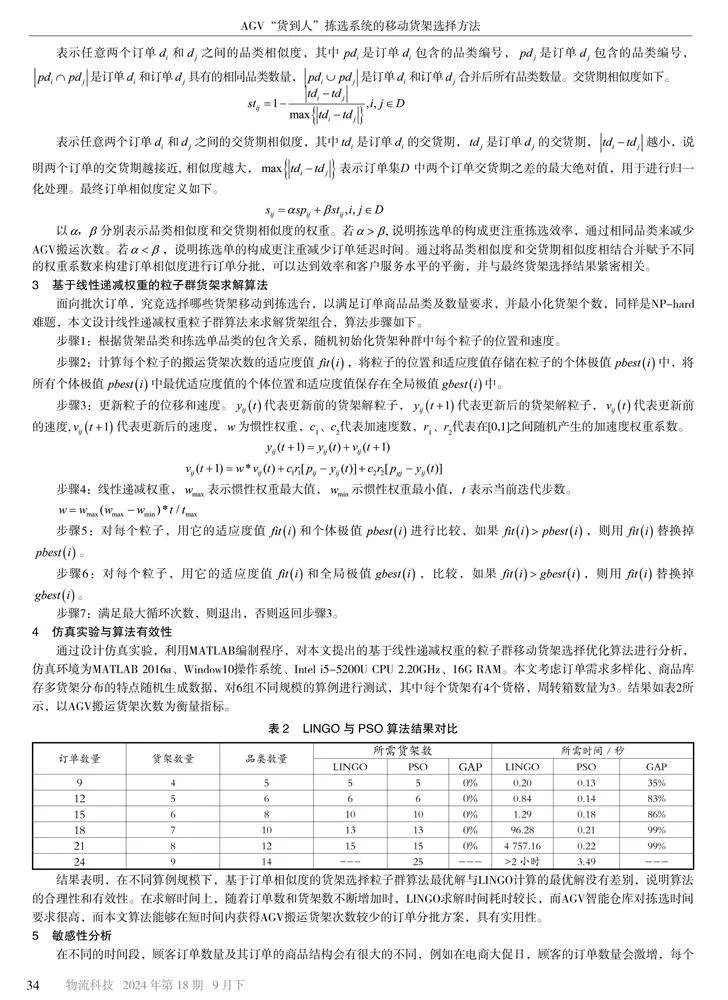
实验结果表明，在同样的货架数量、品类数量和批次数情况下，随着订单数量的增加，AGV搬运货架的次数只在一个很小范围内波动，说明批次订单数量对AGV搬运货架次数的影响很小，如图4所示。

5.5 总体均值的区间估计

在现实生活中，搬运货架次数分布服从正态分布或者近似地用正态分布刻画，上述敏感性分析中，仅使用了样本均值来估计总体均值，即点估计法。使用点估计对总体的未知参数进行估计时，难免有一些误差，究竟估计量的值与真值相差多少，需要进一步寻找总体均值的范围，并应该具有一定的可靠程度，在此使用区间估计法，进一步根据样本数字特征推断总体的数字特征，基本步骤如下。

步骤1：计算样本均值。

步骤2：计算样本方差。

步骤3：使用T统计量对总体均值进行区间估计，其中为样本容量，T统计量服从自由度为的分布。

步骤4：取检验水平=0.05，则区间[]称为的95%的置信区间，分别称为置信下限和置信上限。

根据计算，可以得到批次数量、品类数量、货架数量、订单数量分别对搬运次数的总体均值的95%的置信区间，如表7—10所示。

6 结 论

移动货架仓库中的货架选择问题是针对一批订单的拣选需求，构建满足订单拣选需求、所需要货架数量最小化的数学优化问题，本文通过设计基于订单相似度的订单分批算法和线性递减权重的粒子群货架选择算法，来求解该问题。最后实验结果表明，本文设计的算法在算例测试中有较好的表现，算法可以得到较优的解决方案，且耗时相较于Lingo更少。通过敏感性分析，发现批次数量对AGV搬运货架次数的影响显著，分批越多，AGV搬运货架的次数也呈等倍数增长；品类数量的增加，对AGV搬运货架次数的影响逐渐趋于平缓；在满足商品储存数量情况下，货架数量的增加，会导致AGV搬运货架的次数变多；对同一拣选仓库来说，订单数量的增加，订单数量对AGV搬运货架次数的影响很小。最后为探究点估计对总体均值估计带来的误差，进一步寻找了置信度为95%的总体均值的置信区间，提升了这些发现的可靠性。

参考文献：

[1] DE KOSTER R，LE-DUC T，ROODBERGEN K J. Design and control of warehouse order picking：A literature review[J].European Journal of Operational Research，2007，182（2）：481-501.

[2] KOCH S，WÄSCHER G. A grouping genetic algorithm for the Order Batching Problem in distribution warehouses[J]. Journal ofBusiness Economics，2016，86（1）：131-153.

[3] HONG S. Order batch formations for less picker blocking in a narrow-aisle picking system[J]. Industrial Engineering andManagement Systems，2015，14（3）：289-298.

[4] 王转，裴泽平. 启发式路径下节约里程的订单分批算法 [J]. 计算机工程与应用，2018，54（23）：203-209.

[5] ARDJMAND E，SHAKERI H，SINGH M，et al. Minimizing order picking makespan with multiple pickers in a wave pickingwarehouse[J]. International Journal of Production Economics，2018，206：169-183.

[6] JIANG Zhongzhong，WAN Mingzhong，PEI Zhi，et al. Spatial and temporal optimization for smart warehouses with fast turnover[J/OL]. Computers & Operations Research，2021，125，105091.[2024-02-20]. https：//doi.org/10.1016/j.cor.2020.105091.

[7] 王旭坪，张珺，易彩玉. B2C 电子商务环境下订单拣选与配送联合调度优化[J]. 中国管理科学，2016，24（7）： 101-109.

[8] 罗晓萌，夏雪垠，李建斌.快消品电子商务仓储订单批次问题研究[J]. 系统科学与数学，2016，36（6）：847-859.

[9] MENÉNDEZ S，PARDO E G，ALONSO-AYUSO A，et al. Variable neighborhood search strategies for the order batchingproblem[J]. Computers & Operations Research，2017，78（2）：500-512.

[10] JÜNEMANN R. Materialfluß und logistik—Systematische grundlagen mit praxisbeispielen[M]. Berlin：Aufl.，1989：18.

[11] ENRIGHT J J，WURMAN P R. Optimization and coordinated autonomy in mobile fulfillment systems[C]//AAAIWS'11-09：Proceedings of the 9th AAAI Conference on Automated Action Planning for Autonomous Mobile Robots，2011：33-38.

[12] BOYAEN N，DE KOSTER R，FÜßLER D. The forgotten sons：Warehousing systems for brick-and-mortar retail chains[J].European Journal of Operational Research，2021，288（2）：361-381.

[13] AZADEH K，DE KOSTER R，ROY D. Robotized and automated warehouse systems：Review and recent developments[J].Transportation Science，2019，53（4）：917-945.

[14] XIANG Xi，LIU Changchun，MIAO Lixin. Storage assignment and order batching problem in Kiva mobile fulfilment system[J].Engineering Optimization，2018，50（11）：1941-1962.

[15] ROY D，NIGAM S，DE KOSTER R，et al. Robot-storage zone assignment strategies in mobile fulfillment systems[J].Transportation Research Part E：Logistics and Transportation Review，2019，122：119-142.

[16] YANG Xiying，HUA Guowei，HU Linyuan，et al. Joint optimization of order sequencing and rack scheduling in therobotic mobile fulfilment system[J/OL].Computers&Operations Research，2021，135：105467.[2024-02-25].https：//doi.org/10.1016/j.cor.2021.105467.

[17] BOYSEN N，BRISKORN D，EMDE S. Parts-to-picker based order processing in a rack moving mobile robots environment[J].European Journal of Operational Research，2017，262（2）：550-562.

[18] 秦馨，赵剑道，任楠，等.基于遗传算法的订单分批策略研究[J]. 制造业自动化，2021，43（5）：108-112.

[19] 李珍萍，田宇璇，卜晓奇，等.无人仓系统订单分批问题及K-max聚类算法[J].计算机集成制造系，2021，27（5）：1506-1517.

[20] 张国维，吴凌云.考虑商品数量和商品拣选成本的AGV智能仓库订单分批问题研究[J].运筹与管理，2022，31（12）： 9-15.

[21] 李昆鹏，刘腾博，李文莉.改进自适应遗传算法求解“货到人”拣选系统订单分批问题[J]. 机械工程学报，2023，59（4）： 308-317.

[22] LI Jianbin，HUANG Rihuan，DAI J B. Joint optimization of order batching and picker routing in the online retailer's warehousein China[J]. International Journal of Production Research，2017，55（2）：447-461.