考虑路况与设施失效的应急物流中心选址研究

摘 要：自然灾害发生后，应急物流中心的选址成为决策者面临的紧迫任务之一。选址决策的准确性和合理性直接影响到救援物资的快速分发、救援行动的效率，以及受灾人群的生命安全。文章旨在探讨在自然灾害发生后，基于需求不确定、道路状况和设施失效风险下的应急物流中心选址问题。从两个重要角度出发：一是考虑道路状况系数与弧阻抗系数，从而确定实际运输距离及速度，为应急物流中心选址提供参考；二是建立情景合集，考虑配送中心的设施失效风险，确保受灾地区物资分配的连续性和稳定性。文章基于时间和成本两个目标构建模型并通过NSGA-II算法对其求解，以便决策者根据不同需求选取不同的选址方案，最大限度减少救援时间或救援成本，保障受灾人民和地区的安全和福祉。

关键词：需求不确定；道路状况；应急设施选址；设施失效；NSGA-II

中图分类号：F252 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.18.003

Abstract： After the occurrence of natural disasters， the location of emergency logistics centers has become one of the urgent tasks faced by decision-makers. The accuracy and rationality of site selection decisions have a direct impact on the rapid distribution of relief materials， the efficiency of rescue operations， and the lives of the affected people. The purpose of this paper is to explore the location of emergency logistics centers in the aftermath of natural disasters based on the risk of uncertain demand， road damage and facility failure. The paper starts from two important perspectives： one is to consider the road condition coefficient and arc impedance codfficient to determine the actual transportation distance and time， so as to provide a reference for the location of the emergency logistics center， and the other is to establish a scenario collection to consider the risk of facility failure of the distribution center to ensure the continuity and stability of material distribution in the affected areas. In this paper， the model is constructed based on the two objectives of time and cost， and the NSGA-II algorithm is used to solve it， so that decision-makers can choose different site selection schemes according to different needs， minimize the rescue time or rescue cost， and ensure the safety and well-being of the affected people.

Key words： uncertain demand; road conditions; location of emergency facilities; failure of facilities; NSGA-II

0 引 言

多种类型灾害的频繁发生，给国家的经济建设带来了巨大的损害。尤其值得关注的是，中国70%以上的大城市、半数以上的人口、75%以上的工农业生产值分布在洪水、地震等灾害严重的地区。随着经济的发展，灾害造成的损失也在不断增加。这一现状短期内难以改变，因此我国将长期面临这一严峻考验，所以如何制定合适的应急物流选址方案是一个具有长远意义的研究。

1 研究现状

大量学者针对灾害情况下应急物流中心的选址规划问题从多个角度进行深入研究。第一，对于受灾点需求量的考虑。倪卫红等[1]在受灾点需求量已知情况下，对应急物流中心的选址进行研究；闫森等[2]针对需求的不确定，采用三角模糊数来进行表示；王海军等[3]针对需求的不确定与运输时间的不确定，采用了有机约束的方法对之进行转化。第二，对于路况的考虑 。孙华丽等[4]考虑了道路损毁和道路修复对救援时间的影响；张玲等[5]基于运输过程进行了道路可靠性分析，包括道路等级与复杂度、道路通信能力与路阻系数、道路损毁程度与通行可靠性等。第三，对于选址规划模型的目标。罗淩珊等[6]以设施的最大覆盖量为选址目标建立选址模型；商丽媛等[7]以运输周转量最小为优化目标；孙华丽[8]等建立了以时间最小为选址目标的选址模型；赖志柱[9]等在进行选址时考虑了时间和成本两个目标，并通过一定方法将多目标问题转化为单目标问题。第四，考虑设施失效的情况。周愉峰等[10]建立候选应急物资配送中心中断的情景合集；于冬梅等[11]考虑经济型和服务质量等，建立了一个失效风险的可靠性应急设施选址分配双目标优化模型。孙华丽等[12]采用偏差鲁棒优化这一思想来描述设施失灵风险损失。

因此，本文综合考虑以上四个方面。首先，灾害发生后，短时间内需求点的需求量往往难以获取准确数据，所以本文采用三角模糊数来对需求量进行表达。其次，道路状况也会导致实际运输时间与计划时间不等，影响救援的及时进行，所以本文考虑了路况对通行速度和通行距离的影响，使救援行动更加贴合实际。再次，选址目标的不同也会影响选址的结果，并且采用权重将多目标转化为单目标主观性较强，因此本文通过NSGA-II直接对多目标进行求解，得到一系列最优解供决策者参考。最后，就是在实际灾害发生后，很可能发生二次灾害，进而导致物流中心损毁，影响抗震救灾的正常进行，所以本文考虑了已建立的物流中心损毁时的二次分配，以确保救援行动的正常进行。 综上，本文的选址为综合考虑受灾点需求、道路状况、设施失效的多目标选址，整个过程共分为两个阶段，第一阶段为得到选址方案，第二阶段则是当配送中心建好后，各个配送中心失效情况下的再分配方案获取。

2 路况对选址的影响

灾害发生后，灾区的道路会受到不同程度的损坏，这无疑给物资的及时准确运输带来了更大的困难。若在运输计划制定前未充分考虑这些因素，很可能导致实际运输情况与原先的计划相差甚远，特别是运输物资的到达时间可能会严重延误。这将导致灾害地区的物资需求得不到满足，无疑会加重灾害所带来的损失。因此，本文着重考虑了道路实际通行速度、道路状况系数、广义运输距离等因素，旨在使物资运输过程更加符合实际情况。考虑到道路的实际通行速度，可以更加准确地预估物资运输所需的时间，避免因道路拥堵造成的不可预测延误。而道路状况系数的考虑则有助于评估实际运输距离，从而避免过于理想化预期，保障运输的顺利进行。此外，广义运输距离的综合考虑，可以更好地反映实际运输距离与时间的综合影响，使运输方案更加符合实际需求。

综上所述，通过充分考虑道路实际通行速度、道路状况系数和广义运输距离等因素，我们可以优化物资运输方案，确保物资能够及时、安全地抵达灾害地区，从而最大程度地满足灾区的物资需求，减轻灾害带来的损失。

2.1 路况对道路通行速度的影响

灾害发生后，为了能及时对灾区进行救援，通往灾区的道路可能会因为交通管制而发生拥堵，因此引入弧阻抗系数[13]来表示道路的拥堵状况，，表示道路目前实际的通行流量，表示道路最初设计的通行流量。道路越拥堵则车辆的通行速度就越慢，因此将拥堵状态下车辆的运行速度进行量化，如下所示。

2.2 路况对实际运输距离的影响

如果道路发生损毁，由于绕道等所产生的实际运输距离与原本的运输距离也就有所偏差，于是本文采用孙华丽[13]等所提出的广义运输距离这一概念来描述道路出现损毁后的实际运输距离。

道路状况系数[14]主要与道路的损毁程度以及道路的复杂程度相关。道路的损毁程度主要包括：路面变形程度、道路裂缝程度以及桥梁变形程度，而道路的复杂程度则主要包括：道路建设等级、道路服务等级、路线交叉情况。考虑到上述各个因素对道路通行能力的影响程度不同，因此需要对它们进行权重划分。考虑到传统的层次分析法中，矩阵标度的取值难以准确描述，因此本文采用带有区间数判断矩阵的可拓层次分析法来确定上述6个因素对道路通行能力的影响权重，并建立层次分析结构模型（见表1）。

2.2.1 建立层次结构模型

分析问题并构建所研究问题的层次结构模型。

2.2.2 构造可拓区间数判断矩阵

根据两两比较的标度值和判断原理构造可拓区间数判断矩阵。

2.2.3 求解可拓区间数判断矩阵的特征向量

将可拓区间数矩阵分为左矩阵与右矩阵，即，分别求出左右矩阵的最大特征值以及特征向量。

2.2.4 一致性检验

2.2.5 确定权重

3 模型构建

本文研究的是一个两阶段决策问题，第一阶段是选出配送中心的位置，第二阶段则是不同情境下，当建好的配送中心失效时，如何将失效的配送中心所服务的需求点重新分配给其他的正常工作的配送中心。

3.1 问题描述

当自然灾害发生后，迅速采取救援行动至关重要。其中，最主要的任务之一是从若干应急物流配送中心的候选地址中选出最为合适的一个或多个，同时要满足一定的时间和物资需求量要求。本文以地震为研究对象，将应急物流系统描述为包括基础的配送中心和需求点，并考虑了需求量不确定、道路状况以及设施失效这三大因素。针对受灾点的需求量不确定的情况，本文采用三角模糊数去模糊化的方式来表达需求量。同时，考虑了其对运输计划的影响，以保证运输计划更加合理和真实。由于震后可能还会发生余震，配送中心可能受损失效，因此本文通过建立情景合集来判断配送中心是否会失效，并确保受损的配送中心所服务的需求点能够被其他仍然正常工作且最合适的配送中心服务。在选址目标方面，本文同时考虑救援时间与救援成本两个目标，最后得出一系列最优解供决策者选择。

根据以上描述提出部分假设：一是有若干候选的应急物流配送中心，容量有限。二是每个需求点同一时间只能被一个配送中心服务。三是不同物资可以同车辆运输。四是配送中心车辆足够。五是每个需求点对各类应急物资的需求量都不超过单个应急物流配送中心的存储量。六是设施失效情境下一次最多损毁一个物流中心。

3.3 不确定需求量处理

由于在实际情况下，灾区的物资需求量是很难得到一个精确数字的，因此本文的需求量是用不确定的三角模糊数来表达的，所以需要对其进行适当的处理，使不确定的需求量变为一个准确的数字，本文采用文献[16]中的方式（7）来对三角模糊数进行去模糊化处理，并且为了提高三角模糊数中间值的影响，最终去除模糊化的公式如下。

4 求解算法设计

NSGA-II（Nondominated Sorting Genetic Algorithm II）是一种多目标优化算法，被广泛应用于求解多目标优化问题。它是基于遗传算法的改进版本，由Kalyanmoy Deb于2000年提出。NSGA-II通过模拟自然进化的过程，逐代生成一组解集合，这些解集合包含了多个不同的优化目标。该算法的核心思想是通过遗传算法中的选择、交叉和变异操作，不断优化候选解集合，使其逼近真实的Pareto前沿，即不可再改进的非支配解集。

4.1 NSGA-II算法步骤

第一步：随机生成规模为N的初始化父代种群P0。

第二步：对P0进行非支配排序和拥挤度计算，之后对其进行选择、交叉、变异，生成第一代子种群Q0。

第三步：将P0与Q0合并成规模为2N的新种群R0。

第四步：对R0进行非支配排序、拥挤度计算，并运用精英保留策略生成规模为N的新的父代种群P1。

第五步：对P1执行选择、交叉、变异操作生成子代种群Q1。

第六步：判断迭代次数Gen是否达到最大值，若没有则Gen=Gen+1并返回至第三步；否则，算法运行结束。

4.2 染色体编码

本文采用整数编码方式来对染色体进行编码，整数编码方式是遗传算法中常用的染色体编码方式之一。在整数编码方式下，每个染色体表示一个解，通常是由整数组成的一维数组。由于本文共有5个候选配送中心和15个需求点，所以染色体长度为15，数值的取值范围为1～5。如图1所示。

4.3 交 叉

在遗传算法中，交叉（Crossover）是一种重要的遗传操作，用于产生新的个体，从而增加种群的多样性。本文采用的交叉方式为均匀交叉，在进行交叉操作时，不再按照传统的方式选择固定的交叉点，而是逐个基因位进行随机选择。具体来说，假设父代个体A和B的染色体长度相同为n，进行均匀交叉时，对于每个基因位i，以一定的概率（通常是0.5）选择来自父代A或父代B的基因，并将选中的基因位复制到子代个体的对应位置。这样，就形成了两个全新的子代个体。这种方式有利于增加子代的多样性而且有利于避免局部收敛。

4.4 变 异

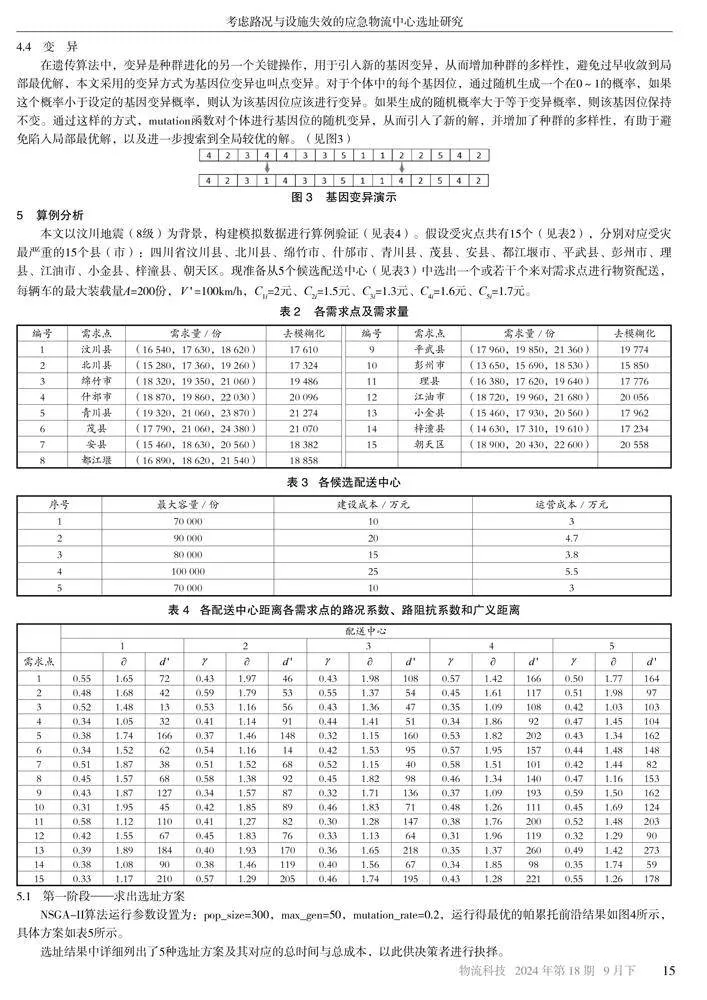
在遗传算法中，变异是种群进化的另一个关键操作，用于引入新的基因变异，从而增加种群的多样性，避免过早收敛到局部最优解，本文采用的变异方式为基因位变异也叫点变异。对于个体中的每个基因位，通过随机生成一个在0～1的概率，如果这个概率小于设定的基因变异概率，则认为该基因位应该进行变异。如果生成的随机概率大于等于变异概率，则该基因位保持不变。通过这样的方式，mutation函数对个体进行基因位的随机变异，从而引入了新的解，并增加了种群的多样性，有助于避免陷入局部最优解，以及进一步搜索到全局较优的解。（见图3）

5 算例分析

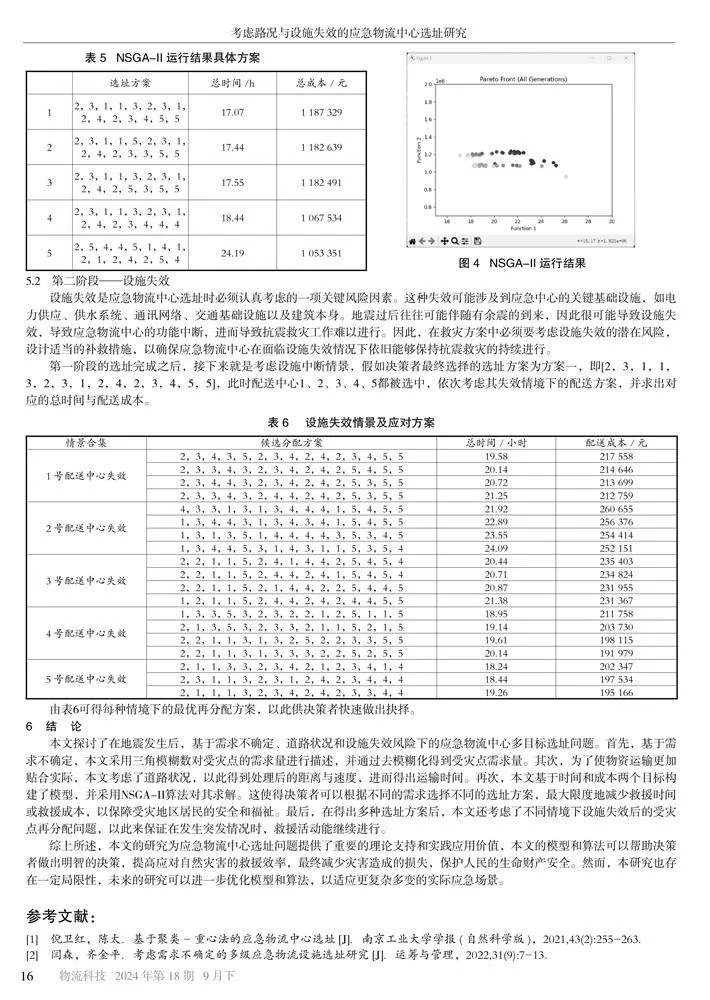
5.1 第一阶段——求出选址方案

5.2 第二阶段——设施失效

设施失效是应急物流中心选址时必须认真考虑的一项关键风险因素。这种失效可能涉及到应急中心的关键基础设施，如电力供应、供水系统、通讯网络、交通基础设施以及建筑本身。地震过后往往可能伴随有余震的到来，因此很可能导致设施失效，导致应急物流中心的功能中断，进而导致抗震救灾工作难以进行。因此，在救灾方案中必须要考虑设施失效的潜在风险，设计适当的补救措施，以确保应急物流中心在面临设施失效情况下依旧能够保持抗震救灾的持续进行。

6 结 论

本文探讨了在地震发生后，基于需求不确定、道路状况和设施失效风险下的应急物流中心多目标选址问题。首先，基于需求不确定，本文采用三角模糊数对受灾点的需求量进行描述，并通过去模糊化得到受灾点需求量。其次，为了使物资运输更加贴合实际，本文考虑了道路状况，以此得到处理后的距离与速度，进而得出运输时间。再次，本文基于时间和成本两个目标构建了模型，并采用NSGA-II算法对其求解。这使得决策者可以根据不同的需求选择不同的选址方案，最大限度地减少救援时间或救援成本，以保障受灾地区居民的安全和福祉。最后，在得出多种选址方案后，本文还考虑了不同情境下设施失效后的受灾点再分配问题，以此来保证在发生突发情况时，救援活动能继续进行。

综上所述，本文的研究为应急物流中心选址问题提供了重要的理论支持和实践应用价值，本文的模型和算法可以帮助决策者做出明智的决策，提高应对自然灾害的救援效率，最终减少灾害造成的损失，保护人民的生命财产安全。然而，本研究也存在一定局限性，未来的研究可以进一步优化模型和算法，以适应更复杂多变的实际应急场景。

参考文献：

[1] 倪卫红，陈太．基于聚类-重心法的应急物流中心选址[J]．南京工业大学学报（自然科学版），2021，43（2）：255-263.

[2] 闫森，齐金平．考虑需求不确定的多级应急物流设施选址研究[J]．运筹与管理，2022，31（9）：7-13.

[3] 王海军，杜丽敬，胡蝶，等．不确定条件下的应急物资配送选址-路径问题[J]．系统管理学报，2015，24（6）：828-834.

[4] 孙华丽，李泽平，马腾．道路修复联合应急设施选址-路径鲁棒优化研究[J]．系统工程理论与实践，2023，43（9）：2701-2716.

[5] 张玲，李继昭．基于道路可靠性的应急救灾选址-路径随机优化问题研究[J]．系统科学与数学，2023，43（10）：2480-2502.

[6] 罗淩珊，黎青松．基于改进集合覆盖模型的应急物流设施选址研究[J]．技术与市场，2021，28（11）：9-11.

[7] 商丽媛，谭清美．不确定应急物流中心选址模型及算法研究[J]．计算机应用研究，2013，30（12）：3603-3605.

[8] 孙华丽，项美康，薛耀锋．不确定信息下应急设施选址-路径鲁棒优化[J]．系统管理学报，2019，28（6）：1126-1133.

[9] 赖志柱，王铮，戈冬梅，等．多目标应急物流中心选址的鲁棒优化模型[J]．运筹与管理，2020，29（5）：74-83.

[10] 周愉峰，陈娜，李志，等．考虑设施中断情景的震后救援初期应急物流网络优化设计[J]．运筹与管理，2020，29（6）：107-112.

[11] 于冬梅，高雷阜，赵世杰．考虑应急设施中断风险与防御的可靠性选址模型研究[J]．运筹与管理，2020，29（9）：53-61.

[12] 孙华丽，项美康．设施失灵风险下不确定需求应急定位-路径鲁棒优化研究[J]．中国管理科学，2020，28（2）：199-207.

[13] 孙华丽，曹文倩，薛耀锋，等．考虑路径风险的需求不确定应急物流定位-路径问题[J]．运筹与管理，2018，27（7）：37-42.

[14] 狄卫民，张鹏阁，杜慧莉．考虑道路状况的应急配发站启用以及配送优化问题[J]．中国安全生产科学技术，2020，16（9）：12-17.

[15] 董伟智，张爽，朱福．基于可拓层次分析法的沥青混合料路用性能评价[J]．吉林大学学报（工学版），2021，51（6）：2137-2143.

[16] 糜万俊，江文奇，戴跃伟．三角模糊数去模糊化对VIKOR妥协解的影响研究[J]．运筹与管理，2019，28（10）：77-82.