多居民点多商户系统顾客需求分布机理

摘 要：根据市场供求关系假设商品价格与顾客需求数量相关，提出多居民点多商户系统中顾客需求分布的均衡机理：对各处居民点的顾客，只选择其所需成本（包括出行成本和商品货币成本）最低的商户，而没有被选择的商户具有更高的成本。构建了等价的数学规划模型来求解多居民点多商户系统中顾客在各商户间的数量分布。证明了模型具有唯一解，并设计了模型的求解算法。并通过算例求解表明，所提出的模型能够真实表达所提出的均衡原则。文章探讨多居民点多商户系统中顾客的选择机理，从而构建顾客需求分布计算模型，可为商户选址优化、商品定价策略优化、顾客需求分析以及各地间交通需求分析等提供基础。

关键词：多居民点多商户系统；分布；均衡；数学规划；算法

中图分类号：F713；U491；U121 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.18.002

Abstract： According to the market supply and demand relationship， it is assumed that the commodity price is related to the customer demand， and the equilibrium mechanism of customer demand distribution in multi-residential and multi-merchant system is proposed： Customers in different settlements only choose the merchants with the lowest costs （including travel costs and commodity currency costs）， while those who are not selected have higher costs. An equivalent mathematical programming model is constructed to solve the quantity distribution of customers among merchants in a multi-residential and multi-merchant system. It is proved that the model has a unique solution and the algorithm of the model is proposed. An example is given to show that the proposed model can truly express the proposed equilibrium principle. This study explores the customer selection mechanism in multi-residential and multi-merchant systems， and builds a customer demand distribution calculation model， which can provide a basis for merchant location optimization， commodity pricing strategy optimization， customer demand analysis， and traffic demand analysis.

Key words： multi-residential and multi-merchant system; distribution; equilibrium; mathematical programming; algorithm

0 引 言

在一个多居民点多商户系统中，这里的多居民点和多商户可分布在某个城市的某块区域上，也可以是更大的范围（如整个城市、国家层面的某个区域或整个国家层面）。针对某类商品，每个居民点的居民总是期望选择成本最小的商户购买该商品。这里的成本包括居民点到该商户的交通成本（指居民点到该商户的出行时间成本，对于大范围来说也可以是物流成本）以及商品购买所需的货币价格。而对于商户来说，其总是追求利润最大化，根据市场商品价格供需规律，商品定价总是随着商品需求增加而增加。因此，这里就有一个多居民点顾客需求在多商户系统中的数量分布问题，很明显它是和居民点到商户的交通成本以及各商户的该商品定价有关的。从选择机理层面探求顾客需求分布可为商户选址优化、商品定价策略优化、顾客需求分析以及各地间交通需求分析等提供基础。

一些国外文献基于一价定理和冰川模型来研究市场分割对商品价差的影响，尤其是经合组织（OECD）各国内部不同地区间的价格差异[1]。由于市场分割产生的交易成本可能会导致商品价格持续偏离一价定理，因此冰川（iceberg）模型对此进行了各种拓展，认为市场分割和市场摩擦带来的交易成本使两地价差在某个区间随机波动。O' Connell等[2]进一步拓展了冰川模型，认为市场摩擦产生的交易成本主要来自运输成本和贸易壁垒等因素。Borraz等 [3]发现相邻城市相距10公里的超市间价格差异与城市内相距30公里的超市间价格差异是相同的，边界使距离增加了两倍。国内的黄新飞等[4]基于长三角15个城市的实证研究，分析了价格差异、市场分割与边界效应。王彪等[5]分析了我国集中带量采购中选药品价格的差异和区域分布。刘发跃等[6]从城市规模、区域和市场化进程等角度对城市间商品价差进行比较和差异分解，并建立面板模型分析其影响因素。行伟波等[7]采用1995—2005年中国城市间33类生产资料价格数据来分析中国的产品市场一体化，根据Levin-Lin-Chu面板单位根方法来检验城市间产品价格差异的长期收敛性。王永进等[8]研究表明高铁开通带来的人员流动能通过促进要素市场一体化和地区间商务往来，显著降低城市间商品价格差异，由此促进地区间产品市场的一体化。陈梦根[9]证实地区价格与收入水平呈显著的正相关关系，而经济结构、外商投资、出口规模、人口密度、交通条件等因素对地区物价水平具有不同程度的影响。刘发跃等[10]认为地区间价格差异反映了市场分割的程度，劳动力成本和居住成本正成为城市间价格差异的重要来源。

然而，虽然一些研究已关注到了地区间交通条件和运输成本对价格差异的影响，但这主要是一些定性的或统计学的分析，而针对多居民点多商户情况下顾客需求的数量分布计算模型目前尚未见有研究。这需要结合效用分析、均衡原理，并通过系统分析和优化方法，构建数学规划模型，并通过对模型的优化求解来得到顾客在各商户间的数量分布。这正是本文的目的和主要工作。

1 模 型

1.1 问题分析

一般来说，各居民点的顾客总是选择最低成本（包括购买商品的货币支出及交通成本）的商户购买某商品；商户对该商品的定价总是与顾客数有关的，根据市场规律，商品价格随顾客需求增加而增加；而当某商户定价较高，则会损失一些顾客（顾客会选择其它定价较低的商户）。这样，最终会达到一种平衡：对各处居民点的顾客，只选择其所需成本（包括出行成本和商品货币成本）最低的商户，而没有被选择的商户具有更高的成本。均衡原理在交通规划中被广泛使用，用于表示给定起终点的一定数量的出行需求总是选择最短的路径，而没有被选择的路径具有更多的费用[11-12]。本文研究顾客在商户中的分布均衡可借鉴其原理并构建相应的数学模型。商户和居民点的分布见图1。

1.2 符号和变量

1.3 前提和假设

第一，本文只针对一种商品，如果是多种商品，则对每种商品分别建模即可。

第二，假定顾客和商户都是理性的，即顾客总是选择最低成本（包括购买商品的货币支出及交通成本）的商户购买该商品；而商户总是追求利润最大化，根据市场商品价格供需规律，商品定价总是随着商品需求增加而增加，反之，顾客少则需降价促销。

第三，对每个商户，不存在断货情况，即只要有顾客总是会有源源不断的货物供给。

第四，系统完全透明，即从各居民点到各商户的交通成本是已知的且固定的，对每个商户该商品的价格（及其变动）信息各处居民点的居民也是完全知晓的。

1.4 均衡原则及模型建立

2 模型解法

3 算 例

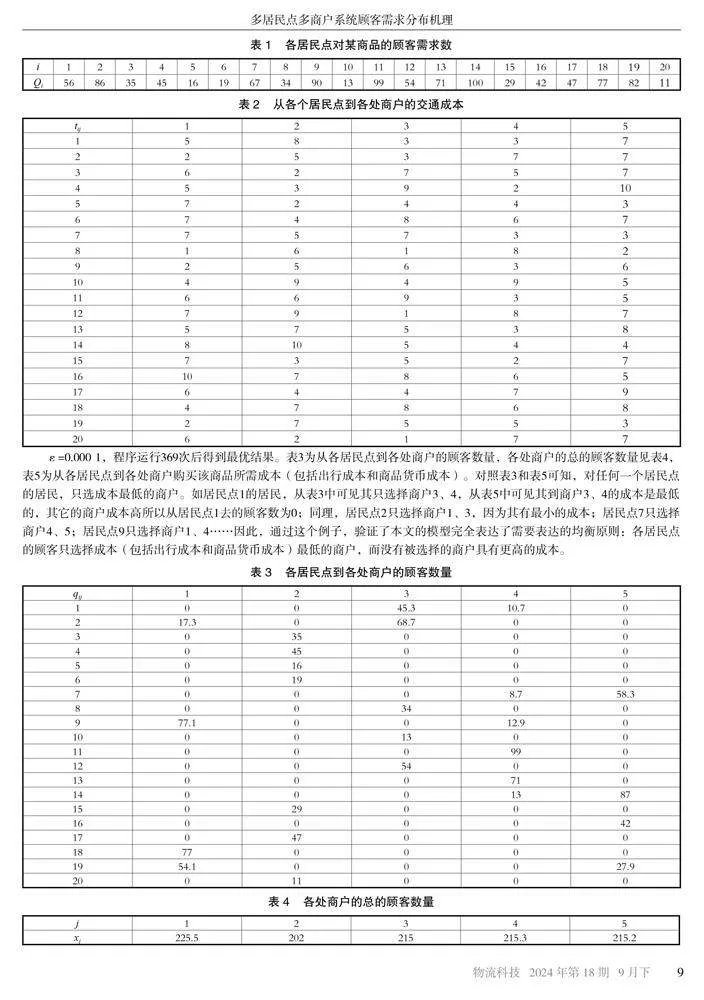
ε=0.000 1，程序运行369次后得到最优结果。表3为从各居民点到各处商户的顾客数量，各处商户的总的顾客数量见表4，表5为从各居民点到各处商户购买该商品所需成本（包括出行成本和商品货币成本）。对照表3和表5可知，对任何一个居民点的居民，只选成本最低的商户。如居民点1的居民，从表3中可见其只选择商户3、4，从表5中可见其到商户3、4的成本是最低的，其它的商户成本高所以从居民点1去的顾客数为0；同理，居民点2只选择商户1、3，因为其有最小的成本；居民点7只选择商户4、5；居民点9只选择商户1、4……因此，通过这个例子，验证了本文的模型完全表达了需要表达的均衡原则：各居民点的顾客只选择成本（包括出行成本和商品货币成本）最低的商户，而没有被选择的商户具有更高的成本。

4 结 论

提出了多居民点多商户系统中顾客分布的均衡原理，并构建了等价的数学规划模型，设计了模型的求解算法，并通过算例求解表明，所提出的模型能够真实表达所提出的均衡原则：各居民点的顾客只选择成本（包括出行成本和商品货币成本）最低的商户，而没有被选择的商户具有更高的成本。本研究探讨了多居民点多商户系统中顾客的选择机理，从而构建顾客需求分布计算模型，可为商户选址优化、商品定价策略优化、顾客需求分析以及各地间交通需求分析等提供基础。

参考文献：

[1] DREGER C，KOSFELD R．Do regional price levels converge？[J]．Journal of Economics and Statistics （Jahrbüecher fürNationalökonomie und Statistik），2010，230（3）：274-286.

[2] O' CONNELL P J G，WEI Shang-jin．"The bigger they are，the harder they fall"：Retail price differences across US cities[J].Journal of International Economics，2002，56（1）：21-53.

[3] BORRAZ F，ZIPITRÍA L．Retail price setting in Uruguay[J]．Economics，2012，12（2）：77-109.

[4] 黄新飞，陈珊珊，李腾．价格差异、市场分割与边界效应——基于长三角15个城市的实证研究[J]．经济研究，2014（12）：18-32.

[5] 王彪，张天天，唐啸宇，等．我国集中带量采购中选药品价格差异及区域分布研究[J]．中国卫生政策研究，2023，16（5）：29-33.

[6] 刘发跃，周彬．城市间的商品价格差异及影响因素——基于市场化进程的视角[J]．西南大学学报（社会科学版），2014，40（4）：55-63.

[7] 行伟波，李善同．一价法则、地区价格差异与面板单位根检验[J]．管理科学学报，2010，13（4）：76-84.

[8] 王永进，侯韫韬．人员流动与城市间商品价格差异：来自高铁开通的证据[J]．世界经济，2022，45（1）：206-232.

[9] 陈梦根．价格差异、收入不平等与地区宾大效应[J]．经济学动态，2020（4）：49-63.

[10] 刘发跃，孟望生．异质性会影响城市间价格差异吗？ ——基于ESTAR模型的收敛性分析[J]．浙江工商大学学报，2016（1）：111-121.

[11] 林晓生，顾宇忻，张薇，等．MaaS场景下考虑用户异质性的交通分配模型[J]．交通与运输，2024，40（1）：99-104.

[12] 丁蕾，杭虹利．应急物流优先的交通分配模型及算法[J]．同济大学学报（自然科学版），2022，50（5）：630-634.

[13] 冯春，冯宇杰，罗茂，等．灾害救援中基于用户均衡的应急物资分配优化研究[J]．运筹与管理，2023，32（6）：53-60.