小学数学学习中儿童的关系思维及其表现

摘 要 对关系的寻找、表达和推理就是关系思维。数量关系是数学教与学的核心内容之一，在对关系的关注、概括和表达的过程中必然涉及关系思维。儿童有比较的本能，有寻找相等关系的直觉。关系思维包括寻找关系、表达关系、从一个关系推理出新的关系等。关注关系思维的数学教学就是关注本能、培养直觉的教学。

关 键 词 关系思维；儿童；数学教学

引用格式 薛春波.小学数学学习中儿童的关系思维及其表现[J].教学与管理，2024（26）：42-45.

在解决现实问题的过程中，弄清关系是关键。数量关系是数学教与学中的重要对象，其核心是多和少，具体数量的多与少抽象符号化之后，就变成了数的大与小。随着数学内部知识体系的建立，这种大小关系推演为顺序关系[1]。比较、判断并描述数量之间的大小关系，自然成为数学中非常重要的内容。特别是相等关系，借助相等关系，通过逆向思维寻找问题的解就是算术思维，通过顺向思维建立相等关系，借助代数运算得到未知数的值就是代数思维。对关系的关注、表达、概括和推理等不同层次的思维活动所涉及的就是关系思维，在比较中把握关系的表达对学生的数学学习是非常重要的。在课堂教学中，发展学生的关系思维，可以使教学获得无限广阔的空间[2]。

一、儿童有关注关系的直觉

1.儿童有比较的本能

将自己和他人比较，将他们看到的、想到的、思考的不同类的事物进行比较，是人类的本能。学生对数量的多少是比较敏感的，他们乐于去比较，也经常提出一些与比较有关的问题。比较的结果就是对关系的梳理、表达和概括。

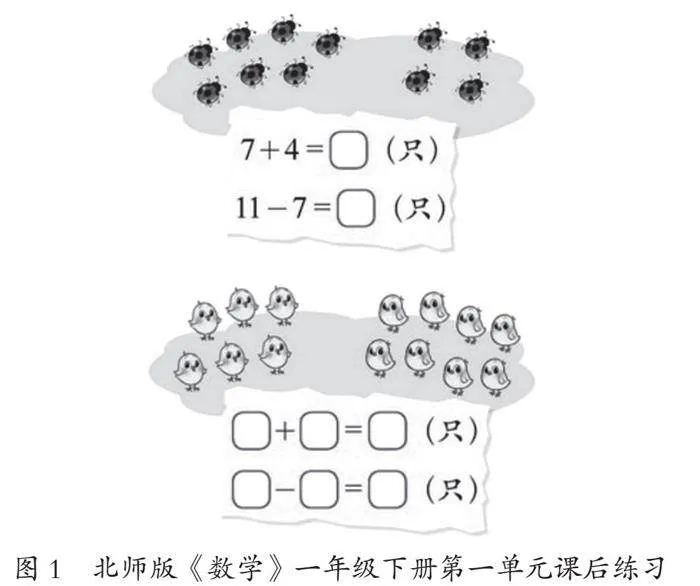
在根据信息提问题的时候，儿童喜欢提出“谁比谁多？多多少？”等问题。一年级教材中有很多看图列式的情境，相对于“从总体中减去部分等于另一部分”的减法关系而言，他们更喜欢写成“一部分比另一部分多多少”的减法算式。举个例子，下面是北师版《数学》一年级下册的一道课后练习题（如图１）。这个题目的本意肯定是按照加减法的互逆关系写出一组加法和减法算式，就像上边的瓢虫图一样。下边的小鸡图对应的算式就应该是6+8=14，14-8=6。但大部分学生会写成8-6=2，即使有上边的例子，也阻止不了学生按照比多少的关系写出减法算式。如果没有上边的示例，那么会有更多的学生用比较的思路来列减法算式，而不是“总体减去部分”。

儿童的数学启蒙最初就是从比较开始的，多了还是少了？大了还是小了？这些都是儿童最初“斤斤计较”过的问题。

2.儿童有找到相等关系的直觉

比较的结果就是相等或者不等的关系，不等关系是生活中比较常见的，但相等关系却是让人着迷的东西。相等关系可以从已知探索未知，可以聚焦到那个唯一的答案，这如同秘境探险一样有魅力。特别是关于分东西的事情，儿童往往只认可“公平”的“平均分”，尽管他们不知道什么是“平均”，但生活中的分享经历，特别是那些儿时经历中因为不平均而引发的争执，让他们只对“公平的平均分”一往情深。

关于“公平”的经验，帮助学生形成了“平均分”的直觉，而这一直觉应该成为学生最初认识除法的起点。先让学生随意分东西，从少量物体分给少数人开始，通过这样的情境能够迅速帮助学生提取记忆中关于“公平分”的记忆。教师从这样的分为2份的“公平的分”开始，再慢慢过渡到分成3份，帮助学生认识到“公平的分”就是数学中的“平均分”，也就是认识“什么是平均分”。接下来，再从较少量的分过渡到较多量的分，从分几个东西到分几十个东西，使学生慢慢体会“怎么分才能平均”，也就是学习平均分的方法。平均分是学生最熟悉的除法问题情境，整数除法的意义主要是在平均分的过程中建构起来的，所以平均分理解得好，整数除法的意义的建构自然就能够水到渠成。

即使是一年级小朋友，也能够直觉到一些相等关系的存在，虽然无法用准确的语言去表达，但他们会不自觉地运用这些相等关系帮助他们找到“捷径”。北师版《数学》一年级下册第一单元退位减法的第一个例题是15-9=？教材中呈现三种主要方法：第一种方法是10-9=1，1+5=6；第二种方法15-5=10，10-4=6；第三种方法9+（6）=15。在用这三种方法计算15-9=6之后，在计算14-8=？的时候，发现学生另辟蹊径，选择第四种方法：因为15-9=6，所以14-8=6。理由是14比15少1，8比9少1。这就是儿童对相等关系的直觉，是他们关注关系的最好例子。在中年级学习平面图形面积的时候，这种关注关系的习惯实际上帮了学生的大忙。并不是每个平面图形都需要重新建构一个面积计算公式，实际上长方形、正方形、平行四边形、三角形、梯形等平面图形的面积公式都是建立在基础关系之上的，发现其中的关系就可以变特殊为一般，关注关系，数学学习就简单得多了。

生活中经历的事情、积累的经验，对儿童的学习是非常重要的。这些经验是他们学习的起点，让他们产生了对知识最初的萌芽认识，这些萌芽认识表现为他们的一些直觉，而这些直觉就成为他们认识一个新概念的前提。教师要善于利用学生的学前经验，巧妙地架构旧经验和新知识之间的联系，而不是对学生的经验视而不见。数学学习原本就是你中有我，我中有你的，没有绝对不相关的数学知识。

二、儿童关系思维的进阶及其表现

关注关系的教学至关重要，思维是数学的灵魂，而关系就是思维的内容。对于关系的关注，包括寻找关系、表达关系、从此关系推理出新的关系。对关系的关注可以从低年级开始，随着年级的升高循序渐进。

1.关系的寻找

寻找关系就是能够找到什么和什么是相关的，随之判断这种相关是有意义的，还是无意义的。在寻找关系的初始阶段，无需过多地从成人的视角去思考儿童所寻找的关系是否有意义，主要是鼓励他们对关系的关注。

如在用3+4+2=9编故事的时候，大部分学生会把相同事物加在一起，但也有学生会编成：我去商场买了3个棒棒糖、4个面包、2杯牛奶，一共买了9样东西。六年级认识比的意义之后，在生活中找比，有的学生会提出男生和女生的比是17：19，桌子和椅子的比是1：1，也有的学生会提出书和椅子的比是3：4。哪些量是相关的量，而这些相关量中哪些相关是有意义的？这对学生是有一定难度的，因为是否有意义需要借助生活经验去评判，而学生缺少的就是生活经验，他们只能在自己的经验范围内思考。

在找关系的时候，读题或读图只是第一步，有感情、有重点地读题也是对关系的一种梳理。教师还可以借助一些策略来梳理关系，如将题目重复给别人听，对题目的复述能够看出读题者对问题的概括程度。对题目理解好的学生，能够概括出问题中的量，并对这些量与量的关系进行初步的概括。画图或画表格，同样能够让无形的关系有形地显现出来。儿童是天生喜欢找关系的，只不过他们的视角和成人会有些不一样，教师切记不要在找关系的时候，过于强调对错，只要他们能够说清楚判断的理由即可。

2.关系的表达

对关系的表达就是在找到关系之后，对关系进行符号化表达。语言是常用的表达方式，借助学具操作同样是对关系的探索和表达，画图也是一种表达，写成等式或不等式还是对关系的量化。一年级就需要强调对关系的语言表达，而不是只停留在会列式计算的层面。例如“乘车”问题，能够用3+4-2=5列式计算并不是唯一的目标，教师还要鼓励学生用“车上原来有3人，上车4人就加上4，下车2人就减去2，现在车上还有5人”这样的语言表达对运算意义的理解和应用。通过画图将“量”画出来是对关系的二次表达，对一些较复杂的问题，画图能够将关系显性化地表达出来。日常教学中，教师往往过于注重画得是否标准，其实图只是一种表达方式，是一个个性化的过程。画图的目的不单纯是为了解决问题，而要将画图等同于语言表达。表格与画图的功能是一样的，当涉及的量开放度比较高的时候，教师可以引导学生通过表格有序地将所有可能的假设呈现出来。用字母表达是一种一般化的表达，抛却了个性化的外衣，直指关系一般性的表达方式。这对低年级学生而言，还是有难度的。比如一年级的时候，即使学生已经认可4+5=9，5+4=9，所以4+5=5+4，教师提出：可以用a+b=b+a来表示这个发现吗？他们齐齐的回答：不可以。可见，对关系的符号化表达，并不能急于求成。字母表达关系是一个一般化的过程，从个别到一般并不是一蹴而就的，一年级学生能够接受个别，但却不可以接受一般。

3.关系的推理

数学关系的概括是一个从已知到未知的不断网络化的过程，这个网络的形成需要推理能力。儿童对推理天生感兴趣，在对学生进行调查的时候，推理情境是他们最喜欢的故事情境。如果把成为一个好的侦探作为学习推理的目标，那么会有更多的孩子爱上数学的。从一个关系推理出新的关系，这是对关系的泛化，更是建立关系与关系之间联系的过程，是一个序列化的过程。学生能够轻松理解“吃掉的+剩下的=全部的”“全部的-吃掉的=剩下的”这组关系。关系推理较好的学生对比较晦涩的关系“商店销售额-成本=盈利”也是可以理解的。一旦找到了关系，并能够建立这些关系之间的联结，就能够实现九九归一的概括。关系的推理对一年级小朋友而言是很难的。他们的思维是叙事性思维，有就事论事的特点，而关系的推理是需要对旧关系有一般性理解的，只有对个别关系的一般化，才能够从一个关系得到另一个关系。

三、发展儿童关系思维的数学课堂教学

关系思维强调用关系去看待世界，看到事物与事物之间的相互关系[3]。注重发展关系思维的课堂教学，重点关注以下几个方面。

1.注重说理，让学生讲清楚为什么

说理就是讲清楚来龙去脉，这是对关系的表达。表达必然涉及逻辑，有逻辑的表达是循序渐进的，不能急于求成。否则会淡化对关系的关注，而陷入形式的僵化。

2.不刻意背诵，延长学生理解的时间

这是很多教师会陷入的误区，认为将公式牢牢地记住了，就是强调关系。公式、定理只是关系的表达形式，并非关系思维的本质，关系思维是一种思维习惯，表现出的典型特征是对关系的敏感度。在面对一个复杂问题时，学生应该更多地关注关系，而不是被是否有公式所限制。延长对公式的理解时间，具体体现在不急于概括公式，甚至不必概括公式。比如长方形和正方形的周长公式就大可不必呈现，周长就是所有边长之和，多余的公式反而会限制儿童对关系本质的关注和思考。

3.多提问题，敢于质疑

善于提问和质疑的学生，必然关注关系，关注自我前后思维逻辑的关系，也关注“我—你”“我—他”之间的关系，关系思维有助于学生质疑精神和批判精神的滋养和发展，对关系的关注能够激发儿童的问题意识，不断在变化中寻找不变。

4.多角度思考问题，通过多样化途径解决问题

从发展关系思维的角度来看，应强调解题途径的多样化，而不是单纯追求解题路径的优化。多样化的解题途径是要被积极鼓励的，实际教学过程中，教师为了追求课堂效率，往往急于总结“简便”方法或一般方法，然而成人的“一般”并非是儿童的“一般”，过早地杜绝儿童原初的思维冲动，会让儿童直奔学习的结果而不是关系。

忽视了关系的数学教学将对学生以后的数学发展造成障碍，对关系的关注能够让思维变得开阔，特别是代数思维，是用更抽象的方式对关系的一般化。在教材研读和教学重构的过程中，教师要有意识地运用关系思维，打通知识点的内在联系，让教学内容结构化、系统化与深刻化[4]。对关系的理解、描述和概括是数学的核心内容。只有当学生把对关系的寻找、概括和表达贯穿于他们的数学学习中时，他们才能够为其后续的数学学习，特别是代数学习做好准备。

参考文献

[1][2] 万伟.对话：一种新的教学精神——从“主体思维”到“关系思维”[J].教育理论与实践，2002（12）：46-49.

[3] 吴晓娟.马克思辩证法的存在基础——从实体思维向关系思维转变[J].现代交际，2021（13）：211-213.

[4] 孙娜，赵国防.“关系思维”视域下的教材解构策略[J].小学教学参考，2021（23）：1-4.

[责任编辑：陈国庆]