“用字母表示数”教学设计及实施

【学情分析】

字母在生活中的应用比较广泛，如厕所的标志WC、扑克牌中的A、J、Q、K等，学生接触也比较多，但对字母表示数量及数量关系有部分学生只知其然而不知其所以然，在学习中会有一定的难度。但学生已具备用字母表示数的经验，用数量关系解决问题的能力，让学生在熟悉和喜爱的活动中分析问题、解决问题，进而理解用字母既能表示一个数，同时又能用含有字母的式子表示另一个数，从而建立字母式子的模型。初步学会用含有字母的式子表示数量的方法；促进学生体会用字母和含有字母的式子表示数的意义及优越性，同时也促使学生学会用字母和式子表示乘法数量关系，以及含有字母的乘法式子的简写，从而促进学生由算术思维到代数思维的过渡。

【教学内容】

小学数学北师大版四年级下册“用字母表示数”。

【教学目标】

1.结合具体情境，会用字母表示数和数量关系。经历探索用字母表示数的过程，体会用字母表示数的必要性，发展抽象概括能力，渗透函数思想。

2.在探索用字母表示数的过程中，感受符号的简洁美和符号化思想。

3.在探索过程中，激发学生学习数学的兴趣和积极主动的探索勇气。

【教学重难点】

会用含有字母的式子表示数量、数量关系，理解含有字母的式子所表示的意思。

【教学过程】

（一）课前谈话，做铺垫

师：孩子们，你们知道老师姓什么吗？

生：姓张。

师：你们怎么称呼我呢？

生：张老师。

师：在课堂上，你们喊“张老师”是指我，如果出了教室，有人喊“张老师”，一定是在喊我吗？

生：不一定，因为姓张的老师都是张老师。

师：看来“张老师”这个称呼是受范围限制的。

（二）激趣导入，揭课题

师：老师手里有六张不同数字的扑克牌，我来抽牌。我抽2、4、6、8、10，同学们猜接下去一张会是几？

生：是Q。

师：为什么是Q？

生：Q代表12。

师：看来用字母可以表示一个数，这节课我们就来探讨“用字母表示数”。

板书课题。

（设计意图：有趣的情境导入瞬间让学生爱上数学课，从学生已有的知识经验出发，用扑克牌引入课堂体验规律，同时初步感知用字母可以表示一个固定的数，从中体会数学与生活的密切联系。）

（三）课中活动，探新知

★活动一：玩扑克牌

1.用字母可以表示一个固定的数。

师：刚才用字母Q表示12，还有这样的例子吗？

生：K表示13，J表示11，A表示1。

师：这些字母表示的是一个什么样的数？

生：固定的数。

板书：字母→固定的数。

2.用字母可以表示一个未知数。

师：一副扑克牌有多少张？

生：54张。

师：老师随意抽出一部分牌，放一边，剩下的这一部分有多少张？你来猜猜看。

生猜数。

师：到底有多少张？我也不知道。剩下的这部分扑克牌有多少张呢？

预设：用一个字母x表示它的数量。

师：看来用字母还可以表示一个什么数？

预设：“不确定的数”或“未知数”。

板书：未知数

师：这个字母可以是56吗？可以是分数吗？可以是小数吗？看来用字母表示一个未知数是有范围的。

板书：范围

（设计意图：通过玩有趣的扑克游戏，对比发现用字母既可以表示一个固定的数，又可以表示一个未知数，这样的设计能刺激学生的好奇心，进而激发学生的参与意识，为后面的研究做铺垫。）

★活动二：儿歌接龙

1.用字母表示任何数。

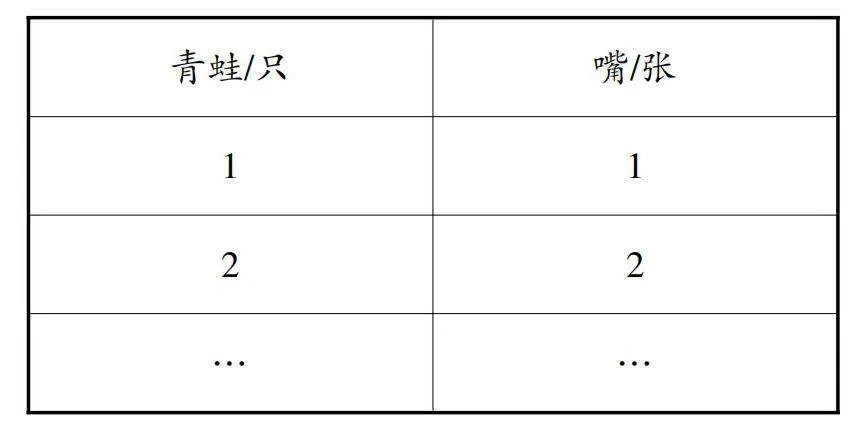
生活中用字母表示数的例子有很多，请看大屏幕——儿歌接龙。“1只青蛙1张嘴，2只青蛙2张嘴，3只青蛙3张嘴……”教师故意不喊停，让学生一直接下去。学生念儿歌的同时PPT出示：

师：为什么停了？

生：念不完。

师：你能不能想办法用一句话概括出所有的情况呢？

a只青蛙a张嘴。

师：你发现了什么？

预设：青蛙的只数=青蛙嘴的张数；字母a可以表示任何数；它的范围是不包含0的自然数。

板书：任何数（范围）

2.含有字母的式子既可以表示数量，还可以表示数量关系。

师：在儿歌中前后两个数量相等时，可以用同一个字母表示，好简单！

PPT出示儿歌接龙：

1只青蛙4条腿

2只青蛙8条腿

……

7只青蛙（ ）条腿

8只青蛙（ ）条腿

9只青蛙（ ）条腿

师：7只青蛙多少条腿？8只呢？9只呢？你是怎么想的？

生：青蛙腿的条数=青蛙的只数×4，所以7只……

师：继续往下接能说完吗？你能不能一次性概括出所有的情况呢？小组讨论。

PPT出示：

①a只青蛙a条腿 ②a只青蛙b条腿 ③a只青蛙4×a条腿

你同意这些想法吗？说明理由。

预设：

①不正确。因为青蛙的只数不等于腿的条数。

②不正确。因为a和b只能分别表示青蛙的只数和腿的条数，不能体现两者有4倍的数量关系。

③正确。因为a表示的是青蛙的数量，4×a表示腿的数量，也表示“腿的条数=青蛙只数×4”的数量关系。

PPT出示“腿的条数=青蛙只数×4”

小结：含有字母的式子既可以表示一个数，也可以表示数量之间的关系。

板书：含有字母的式子→数量 数量关系

3.自学小知识。（规范含有字母的式子中乘号的写法）

师：你知道4×a还可以怎么写吗？

请自学一个数学小知识，PPT出示：

①字母和字母相乘，乘号可省略为“.”，也可省略不写。如a×b＝a·b＝ab

②字母和数相乘，乘号也可省略为“.”，或不写。但通常数字写在字母前面。如a×3＝3·a＝3a 4×x=4x

4.判断并说明理由。

①a×0.8 写作：a0.8（ ）

②5×6 写作：56（ ）

③a+2 写作：2a（ ）

④a×b 写作：ab（ ）

5.直接写得数。

2.4×a= y×9=

a×b= x+x+x=

6.完善儿歌。（巩固含有字母的式子表示的数量关系）

PPT出示：

1只青蛙1张嘴，2只眼睛4条腿。

2只青蛙2张嘴，4只眼睛8条腿。

……

师：如果一直说下去能说完吗？怎样用一句话概括出所有的情况？

生：a只青蛙a张嘴，2a只眼睛4a条腿。

师：2a表示什么？4a呢？

教师再次强调含有字母的式子既可以表示数量，又可以表示两者的数量关系。

（设计意图：通过贴近生活实际的“数青蛙”儿歌，从永远都读不完的体验中感受到用字母表示数是一种需要，用字母表示青蛙的只数与腿数、嘴数、眼睛数之间的关系，体现了符号意识的核心素养。）

★活动三：猜老师的年龄

师：孩子们，你们刚才通过自主探索发现了这么多的数学知识，真了不起！为了奖励你们，老师想告诉大家一个秘密，想知道老师的年龄吗？猜猜看。

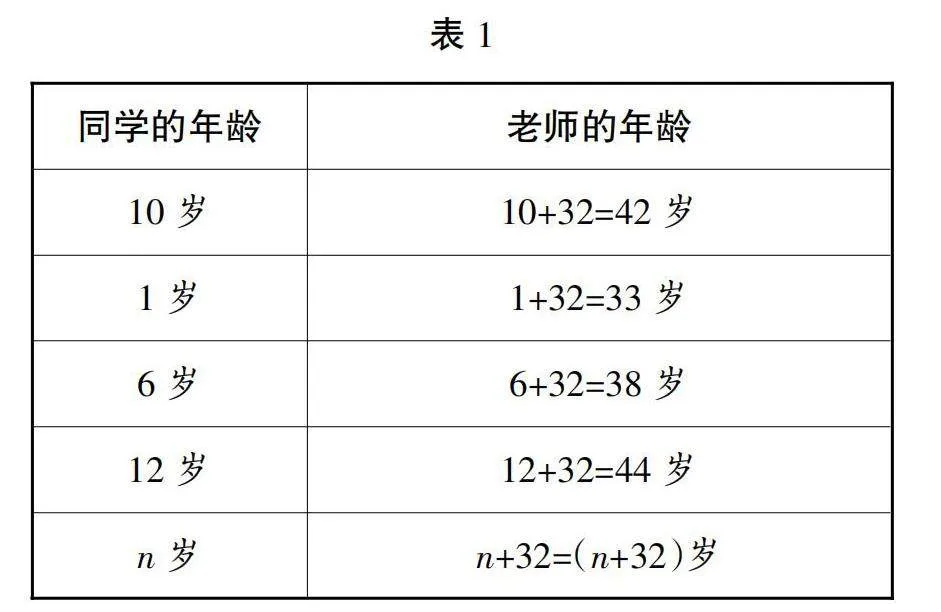
师：我们班很多孩子的年龄是10岁，老师的年龄比这些孩子大32岁，老师多少岁？怎么列式？

师：当你们1岁时，老师多少岁？当你们一年级6岁时，老师多少岁？当你们12岁小学毕业时，老师多少岁？把每一年都说出来麻烦吗？怎样能简单概括出所有的情况？

预设：学生的年龄是n岁时，老师的年龄是（n+32）岁。

根据学生的回答PPT逐次出示表1中的内容。

师：从表1中你知道了什么？

预设：知道老师今年42岁，老师每年都比学生大32岁……

小结：n表示学生的年龄。n+32既可以表示老师的年龄，又可以表示老师比学生大32岁的数量关系，学生和老师的年龄永远相差32岁。

师：n可以是200岁吗？

得出：人的寿命是有范围限制的。

小结：含有字母的式子既可以表示数，又可以表示等量关系。

1.修路队每小时修路a米，上午工作4小时，下午工作3.5小时。

4a表示（ ）；

3.5a表示（ ）；

4a-3.5a表示（ ）。

2.在第一层摆了2个圆片，在第二层摆了3个圆片，在第三层摆了4个圆片，在第n层摆（ ）个圆片。

（设计意图：以熟悉的年龄问题切入，学生的年龄在增长，老师的年龄随之增长，体现了函数思想。）

（四）回顾全课，做总结

今天有什么收获？

（五）延伸课后，做铺垫

课后思考：用字母还可以表示什么？

【板书设计】

用字母表示数

字母→固定的数 未知数 任何数（范围）

含有字母的式子→数量 数量关系

（作者单位：山西省吕梁市离石区龙凤小学）

编辑：温雪莲