几何图形面积计算教学设计

小学阶段的几何知识点教学集中在认识常规几何图形、计算面积等层面上，为了初中几何认识、空间思维、辅助线思维等能力奠定基础，小学数学几何问题中的“复杂图形阴影面积”需要突破。通过学习复杂图形阴影面积，学生能够更进一步认识几何图形的折叠、重合、翻转等，强化学生对几何公式的应用，提升空间思维。

一、教学理念

针对小学阶段的学生，教师应当充分考量其学习能力以及兴趣，通过开放式的教学形式，如“游戏教学”“实践活动”等，来弱化学生自主理解的困难之余，提升学生的自主参与度。教师在课堂中通过画几何图形图纸、旋转拼凑图纸、现实测量等游戏活动方法，把“完善图形”“辅助线”的技巧渗透其中，创设高参与性、高思考性的课堂。

二、学情分析

在此之前，学生已经通过课堂教学完成了正方形、长方形、三角形、梯形、圆形等几个常规几何知识点的学习。在简单解题应用中，学生能够熟练使用面积公式进行几何图形以及生活几何应用题的简单求解。但是经过长时间的综合实践训练得知，学生在面积计算的综合应用上存在诸多难点，其中，最明显的一个问题就是“复杂图形面积”。

“复杂图形面积”中经常存在“阴影面积问题”，也就是图形重叠、翻转、旋转、多个图形交叉形成的阴影面积计算。这类题型中的“阴影面积”不能一眼看出阴影图形所属，无法直接截取边长、高的长度等进行计算，需要学生从复杂图形中推理出已知图形面积，从而确定阴影图形的所属，从而计算各边长，然后计算面积，涉及的方法包括推理、画图、空间、阴影填补、辅助线等，就小学阶段的学生而言，各种方法的综合应用还存在一定难度。

三、教学思路框架图示

四、教学目标

1.认识复杂图形的阴影面积，能够从复杂图形中找到已知图形。

2.熟练使用各个图形的面积计算公式。

3.掌握一定强度的空间几何思维，能够做到完善图形、辅助线技巧的基本掌握。

4.逐步掌握复杂图形阴影面积计算技巧，为初中立体几何学习奠定基础。

五、教学方法

（一）巧设游戏活动，抓住学生的兴趣与学习专注度

小学生对于游戏和动手活动有着极强的兴趣。在游戏活动中，学生能够积极开动大脑，动手操作和尝试，通过动手和直观的感受，形成平面几何思维。所谓游戏活动的动手实践数学教学策略，就是把抽象的概念具象化。这并不是完全没有依据的，《义务教育数学课程标准（2022年版）》中对于“操作”“动手”等关键词的出现频率非常高，明确指出了知识的收获并不是听老师教，练习习题，而是在动手操作与实践的过程中去探究，形成数学概念的深入理解。学生应该有足够的时间和空间经历观察、实验、计算、动手、验证等活动过程。

（二）教师精准引导，把思考的主体地位归还给学生

在学生有兴趣参与课堂学习与动手操作的过程中，教师需要考量的是如何激发学生的主体地位。教师应通过精准的引导来设置思考的方向，利用巧妙的衔接语言，激发学生自主思考的兴趣。因此，课堂中，教师的身份应当是问题引出者、解难答疑者、评价者，切不可做牵着学生思维走的“牵牛者”。学生只有主动思考、积极思考、善于思考，才能不断地熟练技巧，运用公式，提升空间思维能力。

（三）科学开展探究游戏活动，渗透技巧和知识点

游戏活动要渗透技巧和知识点，通过画图、裁纸、拼图、拆分、折纸等多种尝试，让学生理解阴影面积是可以拆分或者合并到某一个已知的几何图形中。在游戏活动的开展中，教师不能仅停留于简单的裁剪、拼图中，更重要的是结合技巧点和重点内容让学生通过自主尝试的裁纸游戏探究如何解决复杂图形阴影面积问题。

六、教学设计及步骤

（一）基础学习教学设计

通过阴影面积复杂图形的呈现，学生认知基本形状与概念。

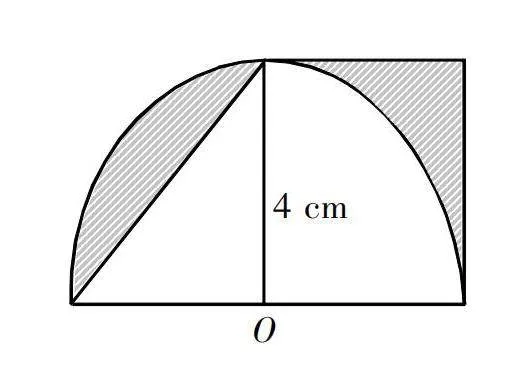
如图1：以O为原点的半圆，半径为4 cm，阴影部分的面积是多少？

这两块阴影面积所属的图形不能直观确定，此时就需要先引导学生思考两块阴影面积是否可以拆分或者能够结合到一个图形中去。此时开展阴影面积图形基本认识的游戏活动。

★游戏活动设置：

1.阴影部分的拆分、重组、合并认识。教师请学生在一张A4纸上画出该图形，并严格按照4 cm半径进行作画。学生作画完成，教师要求部分学生讲述怎么画的，在制作画的过程中发现了哪些问题。其中包括半圆的一部分在正方形为4 cm的图形中，以O为原点的左半边图形在一个半圆的一半的图形中。从作画和发现中去认识复杂图形的阴影面积其实是合并在一个已知图形中的。

2.空间思维的现实化。要求学生把所画的图形进行裁剪，然后沿着正方形以O点向上这一条边进行对折，然后通过测量和观察，确定两个阴影面积重叠后有什么情况发生。实践结果：经过对折后发现两个阴影面积块能够严丝合缝地形成一个三角形，并占据了边长为4 cm的正方形的一半。此时要求学生直接计算面积。

3.补充图形，辅助线思维。学生按照实际游戏活动探究的结果进行阴影面积计算。计算后，教师需要提出问题：“根据折叠我们可以发现两个阴影面积块成为一个三角形，那么还能通过什么方法来验证呢？”让学生自主思考把左边正方形的边长延长，形成一个长方形，也可以发现两个阴影面积可以严丝合缝地重叠形成一个三角形。

4.推理与面积计算公式应用。引导学生思考，刚才是通过实践活动展开计算。如果在不能折叠的情况下应该怎么计算呢？教师板书“圆面积计算公式、正方形面积计算公式”，设置小组活动，让学生开展探究。最后得出圆的半径为4 cm，可以计算出圆的面积，左侧的阴影部分面积为¼个圆的面积减去边长为4 cm的等腰三角形面积，右侧阴影面积为正方形面积减去¼个圆的面积，两者相加即为两个阴影部分的面积。

★教师板书技巧总结：

1.复杂的图形中，阴影面积可以合并到一个已知图形中或者拆分成其他已知图形。

2.阴影面积没有直接计算公式，可以看看阴影面积的图形是否可以延长形成新的已知图形。

3.面积计算公式一定要牢记，所有的阴影面积都可以通过合并图形的相减或者相加或者公用的边以及等边的条件来计算。

（二）深入学习教学设计

深入学习就是提升学生的自主思考、公式应用能力、辅助线思维、图形空间想象思维等能力。

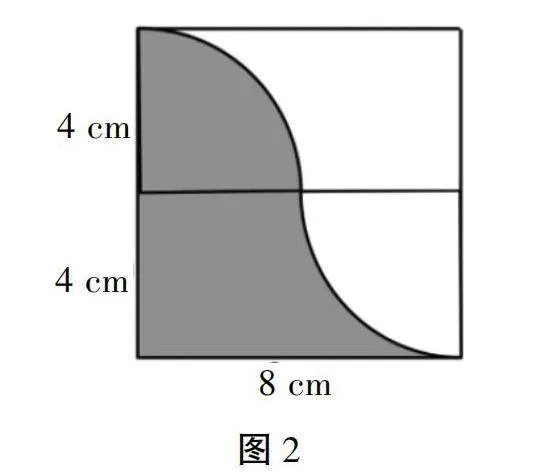
如图2：正方形边长为8 cm，请计算阴影部分面积是多少？

图2更为复杂，学生无从下手。教师针对学生在上一节点学习到的复杂图形拆分和重组，通过平移、旋转、拼凑等知识要点进行提点，提出下列几个思考问题：

△上半部分的阴影面积是否和下半部分的空白处的图形面积一致呢？

△如果上面阴影部分和下面空白处面积一致能否计算出阴影面积呢？

△请尝试在A4纸上画出图形、裁剪，将上下两个长方形通过旋转、对折、平移等操作是否能够证明阴影部分和下面空白处面积一致呢？

★设置游戏活动：

1.在纸上画出这个复杂图形，在作画的过程中，许多学生肯定存在难点，因为上半部分和下半部分着实难以画出。此时，教师提醒学生，是否可以尝试上半部分为半径为4 cm的¼圆画作呢？尝试一下是否能够完成？下半部分留白的地方是否可以尝试半径为4 cm的¼圆画作呢？经过提醒，学生能够完成画作的创作，同时也能够了解到上下部分可能是重合的。

2.对画出的图形利用上下对折或者左右对折去发现。进行裁剪，并尝试平移、旋转、上下左右折叠等方式，学生发现，上下的中线对折后，可以把左上部分阴影面积转换到右边的正方形中去，阴影面积和右下边的留白处形成了一个新的半圆，如此解决思路明了，尝试验证上下部分的面积是否一致也变得简单。

3.要求学生根据游戏活动结果进行计算。但同时提出问题：“同学们，现实解题中，我们不可能裁剪和旋转，我们应该怎么计算呢？还记得前面讲过的补充图形和辅助线吗？我们可不可以创造图形呢？还有刚才我们发现左右对折后，形成了新的图形，是不是可以以此作为辅助线，构造新的已知图形呢？”

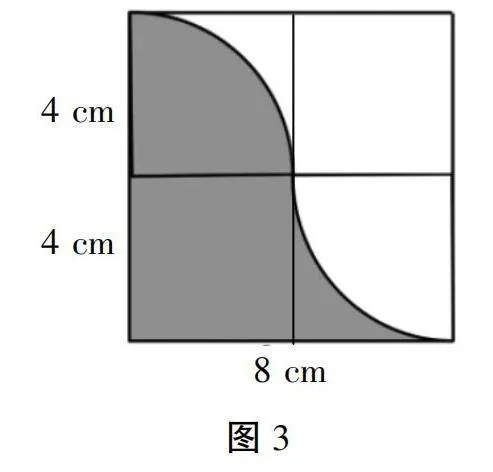
教师板书辅助线图形如图3：

教师提问学生：“设置这样的辅助线有什么帮助呢？是不是能够构造很多已知图形，同时，我们发现，沿着中线所作的辅助线，沿着对折就可以把左边上半部分的阴影面积重叠到右上方的正方形里，这样是不是就有了解题思路呢？”

此时要求学生对所作辅助线思考后，设置小组活动探究，开始面积的计算应用。

★教师板书技巧总结：

1.通过画图、裁纸游戏，我们可以发现，其实大部分阴影面积都可以存在于一个已知图形中，这也是辅助线设置的秘诀。我们的对折线、旋转、构造新的已知图形都是辅助线。

2.一个复杂图形要学会拆分、构造、空间想象来进行初步的尝试。然后找出已知图形，利用正方形、长方形、三角形、圆形的面积计算公式减去留白处就能得到阴影面积。

（三）课堂训练教学设计

设置课堂训练应该遵循“由易到难”的梯度，不宜过多。在游戏活动探究的过程中，学生的思维训练得到极大的提升。每一个例题讲解后，配备的训练题为一个变式题。

训练题的主要考核内容为复杂图形阴影面积的合并、构造新图形等知识点和技巧，强化学生的几何思维能力和公式应用能力。

（作者单位：福建省莆田市仙游县园庄鳌峰小学）

编辑：温雪莲