重视解决问题策略的多样化

培养学生运用多种策略解决数学问题，是数学学习过程中非常重要的一环。教师要引导学生在面对问题时，发散思维，拓宽思路，灵活运用所学知识，尝试不同的解决方法。以北师大版数学小学五年级第七单元“用方程解决问题”中的“相遇问题”为例，通过情境化的教学，启发学生对这个问题进行深入思考。在“相遇问题”这一节，通过引入实际生活中的相遇情景，激发学生对问题的兴趣。这种实际问题的引入能够使学生开阔数学思维，掌握解决实际难题的技能。

学生在收集数据、分析信息的过程中，理解速度、时间、距离之间的关系，然后在小组讨论中，互相交流不同的解决思路。是否可以运用代数法列方程？图形法中标注信息后能得出什么结论？抑或仍可继续思考其他可行方法？这些讨论将拓宽学生的视野，让他们意识到解决一个问题可以有多种角度。在教学中遇到困难时，我们也要理解学生，耐心引导，多给予鼓励。相信通过这次教学，学生能够在灵活运用数学策略上，有很大的进步。

一、教学目标

1.会分析简单实际问题的数量关系，提高用方程解决简单实际问题的能力，培养用方程解决问题的意识。

2.掌握速度、时间、路程之间的数量关系，会根据数量关系解答相遇问题。

3.体验数学与日常生活的密切联系，提高收集信息、处理信息建立模型的能力。

二、教学过程

（一）情景引入

教师播放短视频，配画外音。

星期六，淘气和笑笑约好一起去博物馆参观。两个小朋友为了节省时间，约定从早上8点同时从自己家出发去找对方。你知道他们什么时候会相遇吗？会在哪里相遇呢？怎样解决关于相向运动中的数学问题呢？这就是我们这节课所要研究的内容。

（二）学习新课

（教师利用多媒体出示教材第71页的情景图）

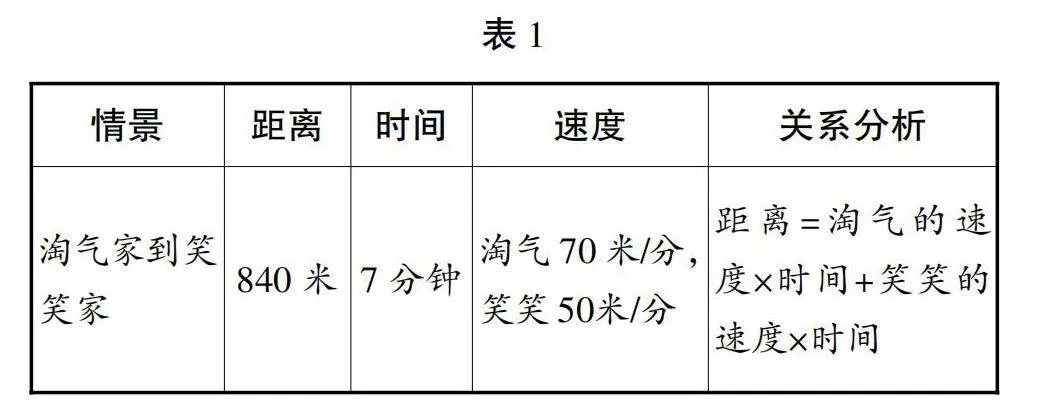
淘气家到笑笑家的路程是840米，两人同时从家出发。淘气的步行速度为70米/分，笑笑的步行速度为50米/分。

（设计意图：通过生动形象的案例引入相遇问题，激发学生的兴趣，让学生体会到这是一个值得思考、有意义的问题。）

师：请大家分组认真观察情景图，从中找出相关的数学信息。

生：淘气的速度为70米/分，笑笑的速度为50米/分，路程是840米，淘气和笑笑的出发时间一样。

（学生分组讨论并收集情景数据，记录在黑板上，如表1所示）

师：大家观察得非常仔细。两人从两地出发，相向而行，经过一段时间，必然会在途中相遇，这类问题就叫作相遇问题。

（教师板书：相遇问题 相向而行）

（设计意图：通过收集数学情景数据，学生在学习过程中养成寻找关键词的习惯。）

师：请大家估计一下，两人会在何处相遇？说一说你的想法。（出示教材第71页问题1）

生1：淘气的速度比笑笑的速度快，相遇时，淘气走的路程应该比笑笑走的路程多。

生2：过一段时间后，淘气距离自己家的距离要远一些，所以估计淘气与笑笑会在邮局附近相遇。

（设计意图：通过分析题目，拓展思维，进一步理解影响相遇问题的条件。）

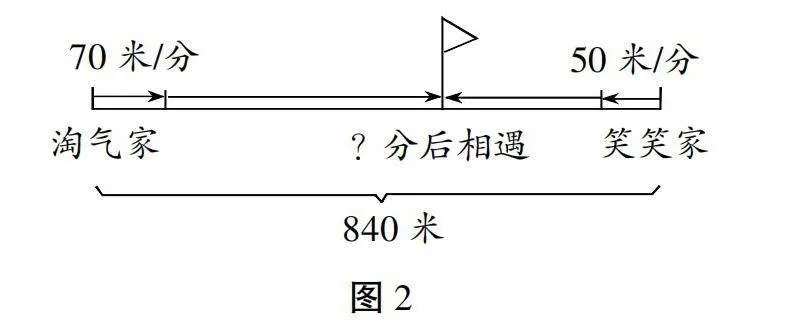
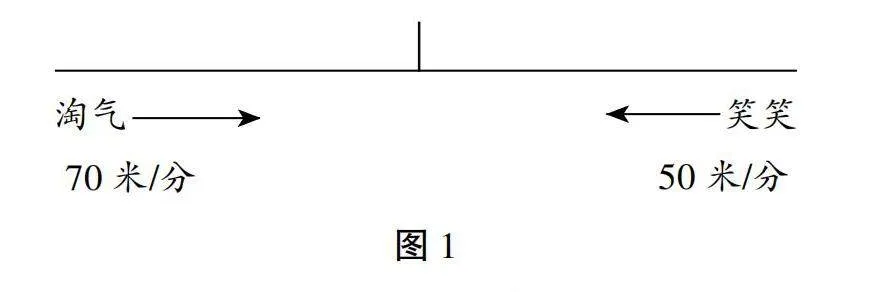
师：那淘气与笑笑出发后多长时间会相遇呢？自己先动手画一画线段图。

教师走下讲台，观察学生的画图情况。5分钟后，教师出示情景线段图。

师：同学请看大屏幕。这幅图描绘了一个很有意思的场景：淘气和笑笑同时从家里出发，在路上相遇。你们能把这个过程想象一下吗？会发生什么？

生1：老师，我觉得淘气走得快，笑笑走得慢，所以淘气走的路程比较远！

生2：我看到淘气和笑笑相遇后，他们走过的路程正好是840米！

师：你们都提出了自己的看法和猜测。要判断他们的相遇点，我们确实要考虑双方的出发时间和移动速度。这就是一个有意思的“相遇问题”。那就让我们一起来解答这个问题吧！

学生通过分析，得出等量关系，即：淘气走的路程+笑笑走的路程=840米。

师：假如我们设他们出发后x分相遇，那么淘气走了多长距离，笑笑走了多长距离呢？

生：淘气走了70x米，笑笑走了50x米。

师：他们两个人走过的距离之和正好是840米。那我们可以列出算式，即：70x+50x=840。

教师展示准确的列式：

解：设出发后x分相遇，那么淘气走了70x米，笑笑走了50x，则

70x+50x=840

120x=840

x=7

答：出发后7分相遇。

（设计意图：本环节以例题为基础，引导学生分析问题，找出其中的等量关系，讲解使用代数列方程解决相遇问题的方法、步骤，加深学生对方法的理解运用。）

师：除了这种方法，还有不同的理解和解题方法吗？

学生思考，教师点拨。

师：因为两人同时出发，所以相遇时所用时间是相同的。两人出发后，每分钟两人的距离缩短 70+50=120（米），即两人的速度和是120米/分。要求两人多长时间相遇，就是求840里面有几个120。等量关系为：（淘气的速度+笑笑的速度）×相遇时间=840（米），根据这个等量关系即可列方程或用除法解决问题。

教师请学生上黑板进行列式。

解：设出发后x分相遇

（70+50）x=840

120x=840

x=7

（设计意图：教师引导学生发散思维，从多方面考虑问题，拓展数学思维。）

师：两位同学的列式非常正确。请大家打开教材第71页，思考第3小题。

如果淘气步行的速度是80米/分，笑笑步行的速度是60米/分，他们出发后多长时间相遇？

教师请学生自主上讲台讲解。

生：这道题的等量关系没有变，还是速度与路程的关系，只是其中的数量发生了变化。所以运算过程是一样的。解题过程如下：

解：设出发后x分相遇，淘气走了80x米，笑笑走了60x。

80x+60x=840

140x=840

x=6

答：他们出发6分钟后相遇。

师：大家对这节课的知识点都掌握得不错，我们一起来总结一下关键的解题步骤。

生：首先要明确问题，弄清需要求解什么未知数，其次要根据问题情景，利用“路程=速度×时间”的关系，为各个运动者列出路程方程。然后将所有路程方程相加并代入已知的总路程条件，从而得到一个方程，最后解这个方程，求出未知数x。

师：概括得很好。确实，借助代数方程描述运动规律，并结合已知条件列方程求解，是解决这类相遇问题行之有效的途径。你还注意到了哪些需要注意的问题？

生：在列方程时要特别注意单位要一致。

师：你总结得非常全面。运用代数方法解决实际问题，需要合理选择未知数、准确建立方程。保持这种良好的数学建模意识，并通过更多实践不断锻炼，你在解决复杂问题方面就能日益娴熟。

三、课堂小结

1.相遇问题中的等量关系是什么？

2.学完这节课，你对用方程解决实际问题有了哪些更深入的理解？

四、板书展示

相遇问题

相向而行

路程=速度×时间

五、课后巩固

1.甲、乙两列高铁从A、B两地同时向C地出发，甲的速度是时速250千米，乙的速度是时速300千米，两地间距离是1650千米。请计算两车相遇需要多长时间。

2.甲乙两人从两个村庄A、B开车相向而行，甲开车速度为60千米/时，乙开车速度为40千米/时。已知A、B村庄相距100千米，请问：

（1）两人开车后几小时相遇？

（2）相遇时，相遇点距离A村庄有多远？

3.小明和小红从A、B两地相向而行，小明步行的速度为4千米/时，小红步行的速度为3千米/时。已知A、B两地相距20千米，小明比小红晚出发2小时。请问：

（1）两人多长时间相遇？

（2）相遇点距A有多远？

4.小红和小明相距14千米，准备步行相见，小红每小时走4千米，小明每小时走3千米。如果他们同时出发，求：

（1）他们相遇需要多长时间？

（2）相遇点距小红起点有多远？

六、教学反思

数学问题解决并非只有固定的标准答案，相遇问题就是一个很好的例证。这节课让我认识到，对于一个看似简单的相遇问题，我们也可以灵活运用诸如方程法、图解法、模拟试验法等多种策略去解析。这种多方法并用的思维，让问题解决更全面、严谨，也使学习数学的过程更富有挑战性和趣味性。图表具有直观形象、信息浓缩的特点，在理解和解决问题时能发挥独特作用。教师引导学生合理运用图表，可以将抽象概念转化为具体可视形式，帮助学生对问题建立更立体、更深刻的认知。图表化表达还能将数据、关系等信息高度浓缩，利于记忆和概括，为发现问题本质和规律提供有力支持。因此，我决心在未来重点学习图表的绘制和运用技巧，熟练掌握各类图表的特点和使用场景。

（作者单位：甘肃省白银市靖远县糜滩镇独石小学）

编辑：张俐丽