结构化思维培养的教学策略

结构化思维是一种系统性的思考方式，通过将问题、信息或任务分解成更小、更具体的部分，并理解它们之间的相互关系和组织结构，以便更好地理解、分析和解决问题。这种思维方式强调整合和组织信息的能力，使人能够更清晰地思考复杂的概念或问题。在小学数学教学中，“圆的面积”是一个既重要又具有挑战性的内容。学生对计算圆的面积缺乏直观的理解，难以建立起有效的认知框架。以往的教学方法过于注重传授公式和机械计算，而忽视了学生对圆形面积概念的深入理解。因此，如何培养学生的结构化思维、激发学生的求知欲望，成为当前圆的面积教学亟待解决的问题之一。

一、内容分析

“圆的面积”是北师大版六年级上册的内容，此时的学生正处于数学计算学习的深入阶段和几何知识学习的扩展阶段，因此，“圆的面积”在小学数学教学中具有重要的地位。圆是几何形状中的重要一环，而“圆的面积”学习则是对圆这一基本几何形状的深入理解，有助于培养学生的几何概念。同时，圆的面积计算与学生现实生活关联密切，有着丰富的应用场景。如计算圆形花坛的面积、圆形饼干的面积等。因此，学习“圆的面积”有助于培养学生的实际问题解决能力和数学建模能力。学习“圆的面积”还有助于学生对数学知识的整合和应用。在学习“圆的面积”时，学生需要用到之前所学的相关知识，如圆的直径、半径、周长等概念，以及长方形的面积计算公式。加强结构化思维培养有助于学生将不同知识点联系起来，形成更加完整的数学认知体系，提高数学学习的连贯性和系统性。

二、教学重难点

1.理解圆形的特性是学习圆的面积的基础。学生需要理解圆的基本概念，如圆的直径、半径、周长等。这些概念的理解对后续的面积计算至关重要。如果学生对圆的基本概念不够清晰，将会影响他们对“圆的面积”内容的理解和运用。

2.如何计算圆的面积。掌握面积计算的基本公式，即πr2（其中r为圆的半径）以及能够在应用题型中进行正确计算。除了对公式的记忆外，理解公式的推导过程，对一些学生来说是一项挑战，教师要注意推导案例、步骤演示的运用。

3.理解圆这一曲线图形与三角形、四边形等直线图形的本质区别。与其他几何形状相比，圆的面积计算可能更加抽象和复杂一些。因为圆形没有直角，也没有明显的边界，所以学生会感到难以理解。在教学中，教师需要采用生动形象的教学方法，如使用图形、实物等来帮助学生形象化地理解圆的面积计算过程。

三、教学过程

（一）问题导入

教师：同学们，今天我们要一起探讨一个有趣的问题。假设我们有一个圆形的水池，它的直径是1 m。现在，我们想用0.1 m×0.1 m的地砖来铺设这个水池的底部。你们能想到我们需要多少块地砖吗？

学生：好像需要很多块。

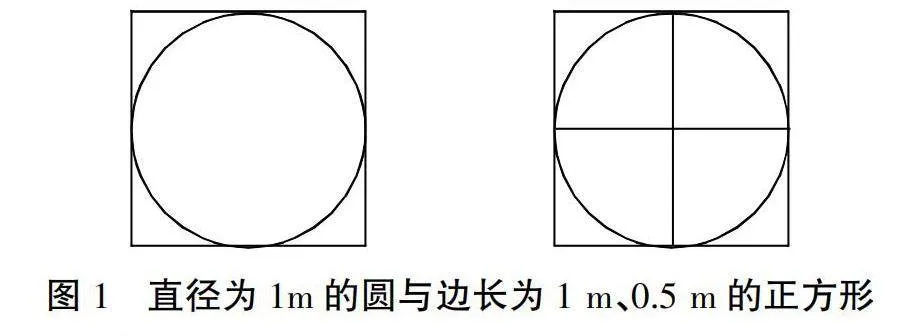
教师：很多块是多少块？这个问题有些复杂，我们将其简化，如果地砖的大小为1m×1m，那么需要多少块？大家可以将直径为1 m的圆与边长为1 m的正方形画出来。

学生：要是1 m×1 m，那么地砖比圆形水池都大，一块都放不进去，如图1（左）。

教师：很好，要是换成0.5 m×0.5 m的地砖呢？用同样的方式画下来。

学生：要是0.5 m×0.5 m的话，4块砖放不下，但是每块砖都会有一部分，如图1（右）。

教师：现在我们回到最初的那个问题，直径为1m的圆形水池需要边长为0.1 m的正方形地砖多少块？

学生：通过上述画图的方式，可以发现大概需要100块地砖。

（设计意图：此案例作为新课的引入，能够自然地过渡到圆的面积计算的教学，为后续的深入学习打下良好的基础。通过铺设地砖的问题，不仅能够激发学生对圆形面积计算的兴趣和好奇心，让学生感受到数学学习的实用性和趣味性，还能够帮助学生建立起圆的面积与正方形面积的联系，形成完整的知识体系。同时，引导学生通过结构化思维来对圆的面积这一知识进行分解，培养学生分析问题、解决问题的能力，以及运用数学知识解决实际问题的能力。）

（二）圆的面积探索

教师：同学们，我们今天要探索一个有趣的数学问题。你们看，我在黑板上画了一个圆，如果我在这个圆里画一个最大的三角形，你们觉得三角形的面积和圆的面积会有什么关系呢？

学生：老师，我觉得三角形的面积肯定比圆的面积小，因为三角形只占据了圆的一部分。

教师：很好，那么画一个正方形呢？

学生：正方形的面积也小于圆的面积，因为正方形也只是圆的一部分。

教师：很好，观察得很仔细。那么，如果我们画一个正五边形呢？它的面积会比正方形大还是小？

学生：同理，正五边形的面积也会小于圆，但是正五边形好像与圆有些相似了，因此，我猜测正五边形的面积与圆的面积更加接近。

教师：猜想很有道理。现在，我们来做个实验，还以上面圆形水池为基础，然后数一下圆内的三角形、正方形和五边形分别占据了多少块边长为0.1m的地砖，以比较这些面积的大小。我们看看实验结果是否验证了你们的猜想。

（学生分组进行活动，教师巡回指导）

教师：好了，各组都完成了计算。现在，请每组代表汇报一下你们的发现。

学生：我们组发现，正五边形的面积确实比正方形和三角形大，但还是没有圆的面积大。

教师：非常棒！同学们总结得很到位。通过这个实验，我们可以得出什么结论呢？

学生：老师，我觉得随着多边形边数的增加，它的面积会越来越接近圆的面积。

教师：当多边形的边数无限增加时，它的形状会无限接近于圆，面积也会无限接近于圆的面积。这就是我们今天探索的重要发现！

（设计意图：引导学生观察、猜想、实验和验证，使其自主探索圆内多边形与圆面积之间的关系。这一过程，旨在培养学生的探究能力、合作交流能力和数学思维能力。同时，直观的图形比较，为后续学习奠定坚实的基础。）

（三）圆的面积推导

在小学数学中，学生学习到圆的面积公式为 πr2（其中r代表圆的半径），很多学生并不知道这一公式是如何推导出来的，因此在学过后很容易遗忘或者对公式记忆产生模糊。这一公式的推导是建立在对圆的性质和几何概念的理解之上的。我们了解到圆是一个几何图形，其边界上的每一点到圆心的距离都相等，这个距离就是圆的半径。而圆的面积则是指圆所覆盖的平面区域大小。推导圆的面积公式的过程中，一种常见的方法是分割法。这种方法将圆划分成多个小扇形，然后将这些扇形组成一个近似的长方形，通过计算长方形的面积来估算圆的面积。随着扇形数量的增加，这个近似值将越来越接近圆的面积。

教师：上面我们通过正方形以及圆内多边形的面积对圆的面积进行了推测，发现圆内多边形的边越多越接近圆的面积。但是这种方法在现实中不实用，不能快速计算出圆的面积。我们来学习一下现实生活中圆的面积计算公式。首先，我们过圆心画出几条直径，同学们发现了什么？

学生：发现圆中多出了几个小扇形。

教师：然后把这些扇形排列起来可以组成一个长方形。

学生：哦，明白了，圆的面积就等于长方形的面积！那我们怎么计算这个长方形的面积呢？

教师：长方形的宽就是圆的半径r，而长方形的长度则是圆的周长的一半πr，所以长方形的面积就是πr×r=πr2。但是这个长方形还有很多小缺口，不完整，所以我们只能说这个面积是圆的面积的一个近似值。

学生：那怎么样才能让这个近似值更准确呢？

教师：当我们把圆划分成的扇形数量越多，这个长方形的形状就会越接近完整，近似值也会越来越接近圆的面积。这就是我们常说的用分割法来逼近圆的面积。

（设计意图：相较于直接告诉学生圆的面积公式，引导学生思考圆与长方形之间的关系，更能激发学生的想象力。在教学中还可以借助多媒体等教学工具，向学生演示圆的扇形部分组合成长方形的过程，提升学生的学习直观性。）

（四）圆的面积应用

在现实生活中，圆的面积应用十分广泛，涉及许多领域，如建筑、工程、地理、艺术等。因此，加强对圆的面积应用案例教学，对提升学生的知识应用能力和结构化思维具有重要意义。继续以上面的圆形水池为例，向学生讲述圆的面积的应用场景。

教师：同学们，回到最初的问题。假设我们有一个直径为1 m的圆形水池，我们需要铺设边长为0.1 m的正方形地砖，那么我们需要多少块地砖呢？

学生：老师，我知道！我们可以先计算出圆的面积，然后再除以每块地砖的面积，就可以知道需要多少块地砖了。

教师：对的，那我们先来计算圆的面积。圆的半径是直径的一半，即0.5 m，所以圆的面积是多少呢？

学生：圆的面积公式是πr2，所以面积就是π×0.52=0.25π m2。

教师：很好，现在我们知道了圆的面积是0.25π m2。那么每块地砖的面积是多少呢？

学生：每块地砖的面积是0.1×0.1=0.01 m2。所以我们需要的地砖数量就是圆的面积除以每块地砖的面积，即（0.25π）/0.01=25π块地砖。

教师：π并不是一个整数，地砖数量怎么可能是π呢？我们需要将π换算成一个合适的数值。一般来说，我们可以取π的近似值3.14来计算。

学生：那么最后我们需要的地砖数量就是25×3.14=78.5块地砖，对吗？

教师：没错！但是由于地砖只能整块购买，所以我们实际需要的地砖数量为79块。所以说，在解决现实问题时，一定要考虑问题实际，运用科学的方法，设计合理的方案，使地砖既要够用，又要防止浪费。

（设计意图：通过这个案例，引导学生将数学知识与实际问题相结合，培养学生的应用能力和解决问题的能力；通过具体的场景让学生理解圆的面积概念，加深对圆形图形特性的认识；通过师生互动，培养学生的合作与沟通能力，促进学生之间的思想交流和合作学习。这样学生不仅学会了如何应用圆的面积公式来解决实际问题，还培养了数学思维和解决实际问题的能力。）

四、总结

通过研究发现结构化思维培养对于小学生理解圆的面积至关重要。以圆形水池铺地砖的问题为起点，引导学生逐步探索圆形面积的相关概念，不仅激发了学生对数学的兴趣，还提高了学生的问题解决能力和逻辑思维能力。在教学过程中，教师要注重学生的参与性，通过让学生自主探索，培养学生的主动学习意识和团队合作精神。因此，结构化思维培养是小学数学教学中一种有效的教学策略，值得在实践中推广和应用。

（作者单位：甘肃省定西市临洮县站滩乡站滩学区）

编辑：曾彦慧