从真实情境出发，培养学生的探究能力

小学数学教学中，倡导教师以培养学生的核心素养为目标，提升学生的关键能力，同时在课堂中创设真实的情境，以问题和实践任务启发学生逐步思考，锻炼学生的数学思维和创造力，培养学生的探究能力，从而提高课堂教学效果。

一、创设真实的旅游情境，探究启思

在小学数学教学中，真实情境发挥着重要的作用，是迅速吸引学生眼球，让学生快速进入课堂状态的重要导入方法。“折线统计图”一课重点引导学生在学习条形统计图的基础上，初步认识单式折线统计图，会绘制折线统计图，知道单式折线统计图的结构和特点，从而向学生渗透统计思想，学会用统计知识解决生活中遇到的问题。为此，教师可以以学生真实生活中的情境引导学生回顾旧知，并在情境探究中启发学生思考。

（一）回顾旧知

在回顾旧知环节，教师借助探究性问题引导学生对数据进行整理和分析，并借助已学过的条形统计图进行数据统计，回顾条形统计图的用法，启发学生思考，以此引入新课知识。

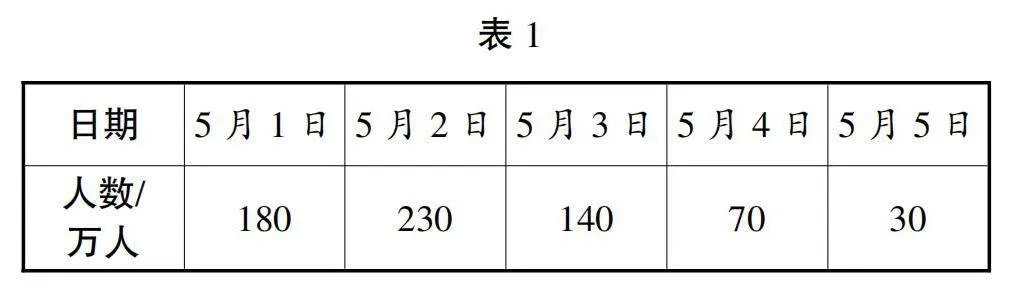
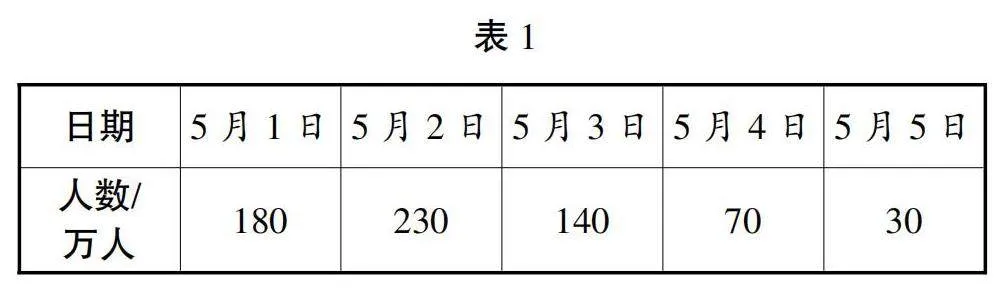
情境创设：随着五一假期的到来，我们很多同学都外出游玩，也有很多游客从各地来到我们这里欣赏美景、品尝美食，感受当地的文化特色。那到底来了多少人，我们本地的魅力有多大呢？下面是五一期间，本地接待游客的人数信息，我制作了统计表（见表1）。

基于上述情境，教师启发学生思考如何把每天的游客数量更直观、形象地表示出来，可用什么方法？

学生提议：制作条形统计图。

教师指导学生回忆条形统计图的绘制方法：条形统计图上有标题、横轴、纵轴。横轴表示日期，纵轴表示人数，并且每个单位长度都表示20万人。

学生自主学习，完成条形统计图的绘制。

（二）问题启思

问题启思环节的重点是将学生的思维代入一个新的情境中，启发学生思考，同时引导学生了解新的知识，提高学生的学习积极性。

在“折线统计图”的教学中，教师针对上述学生绘制的条形统计图提问：“通过条形统计图，我们可以看到五一期间，哪天的游客人数最多？哪天的游客人数最少？”学生自主回答：“通过分析条形统计图，能看出5月2日游客最多，5月5日游客最少。”

教师继续追问：“条形统计图的优势就是能让我们直观地看出数量的多少，展开数据对比。如果我们想从图上看出数据的变化趋势，应该用怎样的统计图呢？比如，我想知道五一期间的游客人数变化情况，哪一天到哪一天是增长的？哪一天到哪一天开始下降？”

基于教师提出的问题，学生展开探究，从而引出本课的学习主题“折线统计图”，怎么绘制“折线统计图”呢？它又有什么优势？今天我们就来学习。

教师结合学生的实际生活，灵活使用教材，创设贴近学生生活的情境，不仅遵循了学生的认知规律，激活了学生的知识经验，易于学生理解和接受，还激发了学生的学习兴趣，考查了学生对条形统计图知识的掌握情况，复习了条形统计图的特点，从而找准新旧知识之间的联系点，为后续教学做好准备。

二、以真实情境为背景探究比较，学习新知

在数学教学中，课堂探究环节重点引导学生学习新知识，掌握知识的形成过程，丰富学生的知识建构，提高学生的学习能力。在“折线统计图”的教学中，教师将探究过程聚焦于学生对折线统计图绘制方法的掌握和应用以及学生识图、读图能力的培养。为此，教师可以从数的探究、点的探究、线的探究以及图的探究四个层面展开尝试。

（一）数的探究

基于学生的知识经验，数的探究旨在引导学生学会从情境问题中抓取关键信息，确定数的类型、单位以及含义，从而绘制出折线统计图所需的表格，为后续图像绘制做好准备。形如：

教师再次展示真实情境：随着旅游行业的发展，本市在五一期间迎来了旅游旺季，很多游客从天南海北来到我们这里，欣赏美景、品尝美食，感受当地的文化特色。据统计，五一当天的游客人数180万cc085226a1e066147c533768bc91798b人次、2日230万人次、3日140万人次、4日70万人次、5日30万人次。之后基于此数据，教师提出问题：请你绘制折线统计图直观地表示五一期间本地游客人数的变化情况。

教师启发学生探究在折线统计图中，我们要表示的是谁和谁的关系？

学生：日期和人数的关系。

教师追问：从题目中，你能得出哪些数据？这些数据的单位是什么？含义是什么？

学生：得出每日游客的人数，数据的单位是“万人”，每个数据表达了当日游客的数量。

教师总结：在条形统计图的绘制过程中，我们先根据题目中的数据画表格，将数据整理到表格中。在折线统计图的绘制中，我们依然这样做，表格的第一栏代表的是日期和人数，快来试试吧。

教师PPT出示表1，学生根据表1中的数据探究折线统计图的绘制。

（二）点的探究

在折线统计图中，学生需要学会描点，这就需要学生明确折线统计图中横轴和纵轴的表达含义以及数据类型，从而找准点的位置。形如：

教师为学生展示空白的统计图，指导学生从表格数据中确定合适的横轴数据类型和单位以及纵轴数据类型和单位。

师：我们将横轴设定为日期，从原点开始划分为5月1日、5月2日、5月3日、5月4日和5月5日，横轴的含义是“日期/天”。我们将纵轴设定为人数，从原点开始划分为40万人次、80万人次、120万人次、160万人次、200万人次、240万人次，纵轴的含义是“人次/万”。

在完成上述操作后，教师启发学生探究，绘制折线统计图的第一步是描点，如何精准地找到这个点的位置呢？

学生：从横轴画竖线、再从纵轴画横线，两个线的交点就是折线统计图点的位置。

教师按照学生的回答展开描点操作，从5月1日处引出一条竖线，再从纵轴180万人次处引出一条横线，两条线的交叉点，描一个圆点。教师启发学生探究思考“这个点表示什么含义”。

学生：这个点对应的横轴是5月1日，对应的纵轴是180万人次，所以这个点表示5月1日有180万人次的游客。教师在该点位置旁边标注数据“180”。

按照上述方法，教师指导学生分组探究，描出其他的点，并标上数据。在学生完成描点后，教师启发学生思考“从描好的这些点中，我们能看出哪些信息”。

学生：有的点高、有的点低；通过点的位置可以看出数量的多少；点高的位置数量大，表示人数多，点低的位置数量小，表示人数少。

通过点的探究，教师引导学生联系条形统计图的绘制方法学习折线统计图的绘制，通过描点操作让学生感受到两种统计图都可以表示数量的多少，以此加深学生的理解，为后续学习“线”和“图”做好准备。

（三）线的探究

线的探究重点是引导学生理解折线统计图中折线表达的含义以及折线方向传递的信息，从而提高学生对折线统计图的绘制能力和理解能力，促进学生形成初步的统计思想。形如：

基于上述学生完成的描点，教师指导他们完成点和点之间的连线。

教师：我们把这些点用线段顺次连接起来，就得到一幅折线统计图。

随后，教师向学生提出探究性问题，鼓励学生探究思考“观察点的位置可以知道数量的多少，那这条起伏变化的折线，可以传递给我们哪些信息呢”。

学生：从5月1日到5月2日，折线是向上的，说明游客数量增加了；从5月2日到5月3日，折线是向下的，说明游客数量减少了。这说明折线的方向能够体现数量的变化。

学生：5月2日到5月3日的折线比5月3日到5月4日的折线更陡峭一些，说明折线的倾斜度能够体现数据变化的大小。

基于学生的回答，教师再次将学生此前完成的统计表与折线统计图进行比对，引导学生认识5月1日到5月2日之间的线段方向向上，表示游客数量在增加，5月2日到5月5日的线段方向向下，表示游客数量在减少。而向下的线段又有平缓和陡峭的区别，表明线段越长、倾斜度越大，表示数量的变化范围越大；线段越短、倾斜度越小，表示数量的变化范围越小。

教师通过线的探究引导学生对折线统计图中线段的特征展开分析，并结合数据表格得出统计结论，从而认识数形结合思想在统计学中的应用，同时促进学生形成推理思维，以此培养学生的探究能力。

（四）图的探究

图的探究重点是引导学生对折线统计图的整体展开分析，引导学生认识折线统计图的特征、优势，同时从折线统计图中观察数据变化，分析数据变化反应的规律，以此获取更多的信息，从而培养学生的数据分析能力以及读图能力、识图能力。形如：

教师鼓励学生以小组为单位，互相交换彼此绘制的折线统计图，并从中找到各自存在的问题。如有的学生忘记标注点旁边的数字；有的学生连线超出点外、有的学生忘记写纵轴和横轴的单位等。教师应针对学生出现的错误展开针对性的讲解，强化学生对折线统计图绘制方法的掌握。

教师提出问题：刚才我们逐段分析了游客人数的增减变化情况。那么从整体上看，五一假期的游客人数呈现什么趋势呢？你能预测一下5月6日或者4月30日游客的数量吗？基于此问题，教师指导学生展开小组探究。

学生：通过观察折线统计图，我们可以看到五一期间本市的游客人数先呈增长趋势（在5月2日达到顶峰），后呈下降趋势（在5月5日达到最低点）。可见，多数人是在5月2日到达本市旅游。

学生：通过观察折线统计图可以预测在4月30日时，只有少部分人选择节前出游，游客人数应该低于180万人次。预测在5月6日时，多数人回到工作岗位，因此人数应该低于30万人次。

师：折线统计图的优势可以帮助我们解决更多新问题，因此适用范围广泛，带给我们的便利性更强。

在学生探究结束后，教师再次提出问题：“折线统计图中通过点的位置可以看出数量的多少，通过变化起伏的折线可以看出数量的增减变化情况，并且能从这些变化中发现数量的发展趋势。那么，依据你的发现，假设我市要在火车站、机场等地开展游客迎接活动，向游客宣传本地的景点、文化、特产等，你认为应该选择哪一天？”基于此问题，教师指导学生展开小组探究。

学生：应该选择5月2日，因为这一天的游客人数最多，宣传效果最好。

师：折线统计图除了能反应数据规律，还能帮助我们解决更多实际问题。

教师引导学生对折线统计图展开分析，从中推理、总结出数据规律，从而培养学生的数学思维，提高学生的学习积极性。

三、结合真实的生活情境拓展探究，思维进阶

（一）折线统计图的应用

生活中的很多问题都可以用折线统计图来解决，直观地反映数据变化的规律，从而为我们提供多样性的数据信息。为此，在教学中，教师可以为学生设计多样化的实际问题，引导学生应用折线统计图展开探究。

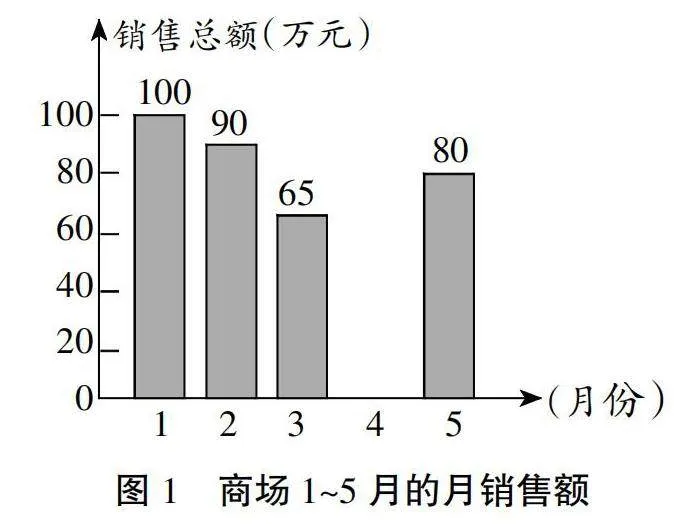
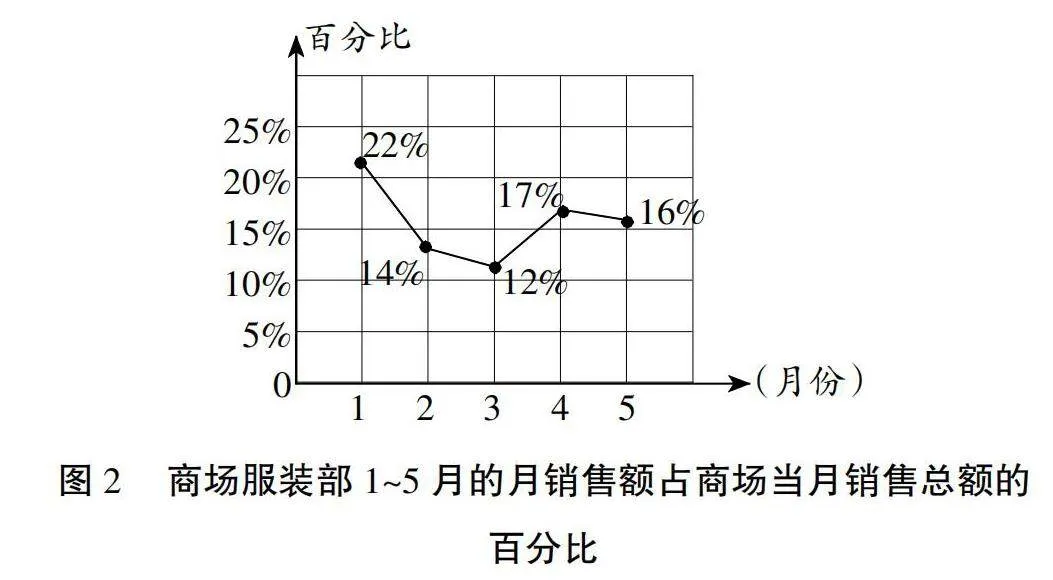
形如，如图1表示的是某综合商场1～5月的月销售额情况，图2表示的是商场服装部1～5月的月销售额占商场当月销售总额的百分比情况。观察图1、图2，解答下面的问题。

1.来自商场财务部的数据报告表明，1～5月份商场销售总额一共是410万元，请求出4月份的销售额，并补充条形统计图。

2.商场服装部2月份的销售额是多少万元？

3.若商场准备增设服装部的店铺，你认为在几月份增加店铺更合适？若服装部准备开展促销活动，提升销售额的占比，你认为几月份最合适？

【问题目标】本题考查学生对条形统计图和折线统计图的读图能力、作图能力，要求学生能从图中找到关键性的数据，并进行运算，以此解决实际问题。

【问题解析】据图1可得，1月、2月、3月、5月的销售总额，再用1～5月的销售总额减去这四个月的销售总额即可得出4月份的销售额。由图2可知，用2月的销售额乘14%即可得出服装部2月份的销售额。服装部的销售额1月份的时候在商场总销售额中占比最大，因此在1月份前后增加店铺更合适。2月份和3月份服装部销售额占商场总销售额最少，因此为了提升销售额的占比，建议在2月份或者3月份开展促销活动。

【详细解答】

（1）410-（100＋90＋65＋80）＝410-335＝75（万元）答：4月份的销售额是75万元。

（2）商场服装部2月的销售额是：90×14%＝12.6（万元）答：商场服装部2月的销售额是12.6万元。

（3）1月份前后增加店铺更合适；2月份或者3月份开展促销活动更合适。

折线统计图的应用探究，可以培养学生的读图能力、绘图能力，引导学生学会用探究思维考虑问题，提升学生解决问题的能力。

（二）折线统计图的实践

在折线统计图的教学中，教师应根据学生的学习情况，为学生设计课后实践任务，鼓励学生将所学知识应用到实际生活中，促进学生学以致用。形如：

实践任务：调查过去六个月的家庭用水情况，统计数据、制作表格，并绘制折线统计图。根据你完成的折线统计图分析出家庭用水的规律。

综上所述，在小学数学教学中，从真实情境出发指导学生展开探究式学习具有突出的实践意义。教师应充分了解学生的学习情况，并结合学生的生活经验创设易于学生理解和接受的课堂情境，并在该情境下引导学生探究课程知识，培养学生的数学思维和创造力，以提升学生的关键能力，实现有效教学。

（作者单位：厦门市集美第二小学）

编辑：赵文静