小学数学“0～9数的认识”单元学习目标和重难点的把握

【摘" "要】针对“0～9数的认识”知识主题单元，应基于其单元知识结构和学生的学习心理过程，把握单元学习目标和重难点。具体而言，先以课程标准、单元知识结构为依据，参考安德森教育目标分类理论，确立九个单元学习目标，并对其进行分解、归类，形成各知识模块的学习目标。再以单元学习目标、学生的学习心理过程和教师的教育教学经验为依据，确定四个单元学习重点和四个单元学习难点，同样对其进行分解、归类，形成各知识模块的学习重难点。以此为基础开展单元整体教学设计，有助于教师在教学中有针对性地突出重点、攻破难点。

【关键词】0～9数的认识；单元整体教学；学习目标；学习重点；学习难点

作为单元整体教学设计的主要抓手，单元学习目标和重难点不仅是衡量教学效果的重要尺度，也是选择教学内容和策略的重要维度。为此，笔者在已确立的单元知识结构［1-2］和学生学习心理过程［3］的基础上，对“0～9数的认识”单元的学习目标和重难点展开探索，将其从单元整体逐步分解至具体的知识模块，以构建可观察、可测量、可评价的学习过程。

一、“0～9数的认识”单元学习目标

为确保教学的有效性，在教学“0～9数的认识”单元之前，教师应以课程标准为上位指导，以单元知识结构为内容基础，以安德森教育目标分类理论为理论支撑，先确立单元学习目标，再将单元学习目标分解为模块学习目标，为后续进一步制定课时学习目标提供直接依据。课时学习目标的制定具体将在组织与安排学习活动时展开。

（一）确立依据

1.上位指导：课程标准

《义务教育数学课程标准（2022年版）》在“课程目标”中强调核心素养及其主要表现在每个学段的发展。“0～9数的认识”单元属于第一学段“数与运算”主题的学习内容，侧重于培养学生形成初步的数感、符号意识和运算能力。在“课程内容”中，则规定了学生要学习的内容范围及需要达到的水平，并对学生应达成的学习表现提出了具体要求，包括认数、读数、写数、数的意义、数位含义、大小比较、加减运算及问题解决等方面，同时提示学生应关注数的认识与运算间的密切联系。

2.内容基础：单元知识结构

“0～9数的认识”单元的内部知识结构以“数感”为素养导向，以“十进位值制”为核心概念，划分为数的意义、数的形式、数的运算三个主模块，并进一步分解为基数、序数、数的顺序、数的大小比较、数的分解与组成、读数、写数、加法运算、减法运算以及连加、连减、加减混合运算十个子模块（如表1）。“0～9数的认识”本身虽未涉及“10”，但已经预设了十进位值制。十进位值制意味着记数遵循满十进一的规则，其基本记数符号包括“0～9”。反之，将“0～9”作为一个整体，说明其所在的记数系统采用十进位值制。

3.理论支撑：安德森教育目标分类理论

安德森教育目标分类理论通过“知识—认知过程”的二维框架，包括事实性知识、概念性知识、程序性知识和元认知知识四个知识维度，以及记忆、理解、应用、分析、评价、创造六个认知过程维度［4］，促使学习目标变得更加清晰、更易于操作。以此为理论支撑把握单元学习目标，有助于有效构建学习路径、选择教学策略及制订评价方式，为“学—教—评”一致性的规划奠定基础。

（二）对“0～9数的认识”单元学习目标的把握

采用行为目标陈述法，从整体上把握“0～9数的认识”单元学习目标。以“形成初步的数感、符号意识和运算能力”为上层的核心素养目标，综合考虑知情意行各个方面，按照本单元的知识结构予以落实。具体目标如下。

● 目标1：能认、读、写0～9各数。

● 目标2：能使用0～9各数表示物体的个数或事物的顺序和位置。

● 目标3：能了解符号“＜”“＝”“＞”的含义，能比较0～9数的大小并用符号表示，能感悟相等和不等关系。

● 目标4：能理解并掌握0～9数的分解与组成。

● 目标5：能在具体情境中了解加减运算的意义，能感悟加减运算之间的互逆关系。

● 目标6：能正确且熟练地计算得数在10以内的加、减、连加、连减和加减混合运算。

● 目标7：能运用0～9各数及其相关的加减运算解决简单的实际问题，能体验数学与现实世界的密切联系。

● 目标8：能感悟0～9是一个整体，能通过类比知道10～19、20～29、30～39等同样可以作为一个整体（十进位值制思想的最初孕伏）。

● 目标9：能提高学习数学的兴趣，建立学好数学的信心，养成专心倾听、认真书写、勇敢表达的学习习惯。

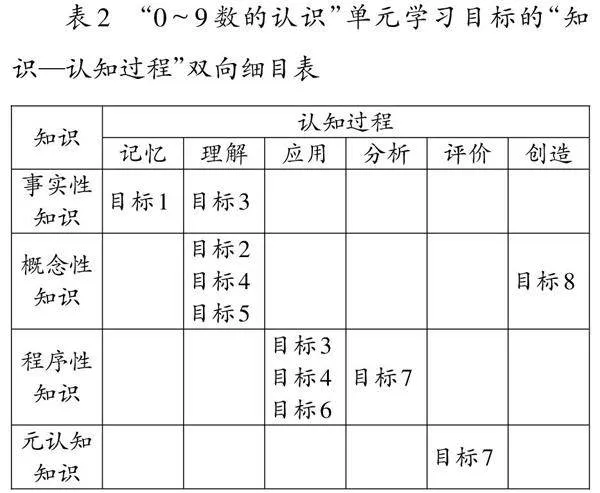
在确立单元学习目标后，利用安德森教育目标分类表，对目标1～8进行归类，形成单元学习目标的“知识—认知过程”双向细目表（如表2）。目标1注重对事实性知识的记忆。目标2涉及0～9的基序数含义，是继续学习0～9数的大小比较、数的顺序、数的分解与组成的概念基础，侧重对概念性知识的理解。目标3中，了解符号的含义侧重对事实性知识的理解，比较大小则侧重对程序性知识的应用。目标4注重对0～9数的分解与组成的理解和掌握，其中“理解”侧重对概念性知识的理解，“掌握”侧重对程序性知识的应用。目标5注重对加减运算意义概念性知识的理解。目标6涉及加减运算的执行或使用，注重对程序性知识的应用。目标7中的运用加减运算解决实际问题，需在区分问题结构的基础上列式并计算，侧重对程序性知识的分析，而体验数学与现实世界的密切联系则体现了应用意识，上升至元认知知识的评价层面。目标8注重核心概念十进位值制的孕伏，强调将0～9中的各个要素加以组合形成整体，并据此类比组织10～19、20～29、30～39等整体，侧重对概念性知识的创造。目标9由于涉及潜在的数学学习情感、态度、价值观等因素，要求在目标1～8之上，故未将其归于分类表中。

（三）对“0～9数的认识”模块学习目标的把握

依据单元知识结构的知识模块划分，将单元学习目标分解为下述模块学习目标（如表3）。其中，目标1归入A2的B6、B7；目标2归入A1的B1、B2、B3；目标3归入A1的B4；目标4归入A1的B5；目标5～7归入A3的B8、B9、B10，且每个子模块都包含运算意义、运算方法、解决实际问题三个方面的小目标；目标8～9贯穿整个学习中，故未将其限定于具体模块。

基于此，利用安德森教育目标分类表，对目标B1～B10进行归类，形成模块学习目标的“知识—认知过程”双向细目表（如表4）。

二、“0～9数的认识”单元学习重难点

确立教学目标后，教师应以单元学习目标为直接来源，以学生的学习心理过程为重要参考，以自身的教育教学经验为辅助依据，先把握单元学习重难点，再将单元学习重难点分解为模块学习重难点。鉴于“0～9数的认识”单元不是每节课都存在重难点，因而将其细化至单元和模块层面就不再继续分解，以此实现对教学的统领与观照。

（一）确立依据

1.直接来源：单元学习目标

单元学习目标是重难点的直接来源，故学习重难点不应游离于学习目标之外。教师应从已确立的学习目标中，筛选出较为重要的知识作为重点，并选择学生实际学习中可能存在的认知困难作为难点。

2.重要参考：学生的学习心理过程

学生的学习心理过程是确立重难点的重要参考。它从生理学和心理学角度为重难点的确立提供了解释，使得学习重难点和学习对象的需求更加契合。为此，笔者通过“一年级新生数感发展水平”测试，诊断学生的学习起点，结合APOS理论预设学生的学习心理过程。即通过“具象—抽象”交替前进的过程，达成各模块认知的螺旋上升，最终整体化为单元概念图式，迁移应用于实际问题的解决中。这提示教师，教学时应侧重考虑抽象的“0～9”能表示具象的实物集合的数量及事物的顺序和位置，并将其列入本单元的学习重点。同时，一年级新生在测试中表现出的薄弱点可能会成为其学习的难点，如难以区分基数和序数、无法灵活运用加减计算的多种策略、在理解数的前后关系及其在序列中的位置上存在困难等，需列入本单元的学习难点。

3.辅助依据：教师教育教学经验

教师的教育教学经验是确立重难点的辅助依据，有助于开展更具针对性的教学，提高教学效率。教师应反思一定时间内的教学实践，总结出不同认知层次和认知特点的学生学习特点，以及适用于自身情况的教学方式和手段。在再次教学相关内容时，他们就能根据学生实际认知水平，有效地辨析学习重点和学习难点，从而为单元学习重难点的设置提供辅助。

（二）对“0～9数的认识”单元学习重难点的把握

1.“0～9数的认识”单元学习重点

依据上述内容，同时参考课程标准、教材、教师参考用书和练习册的知识呈现程度，从已确立的单元学习目标中提炼出以下学习重点。

● 重点1：理解并掌握9以内数的基数、序数含义。

● 重点2：理解并掌握9以内数的大小比较。

● 重点3：准确掌握0～9的标准写法。

● 重点4：理解并掌握加减运算的意义与计算方法。

重点1源于单元学习目标2，从学生的学习心理过程来看，这是学习0～9数的意义与运算的基础，在本单元的学习目标中具有重要的引领地位；重点2源于单元学习目标3，是理解0～9各数之间关系的重要一环；重点3源于单元学习目标1中的“能写0～9各数”，并结合目标9中的“养成认真书写的学习习惯”，进一步归纳为“准确掌握0～9的标准写法”；重点4源于单元学习目标5和单元学习目标6，是对数的意义的进一步应用，它不仅是四则运算学习的重要基础，还是解决实际问题的关键前提。

2.“0～9数的认识”单元学习难点

重点参考一年级新生在数感发展水平测试中表现出的薄弱点，结合教师教育教学经验，从已确立的单元学习目标中寻找学生可能存在的认知困难作为单元学习难点，具体如下。

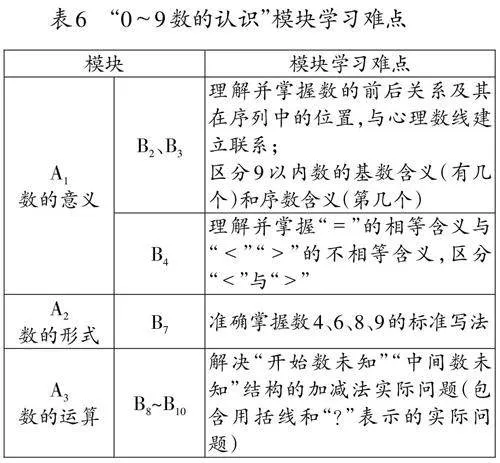
● 难点1：理解并掌握9以内数的序数含义，与基数含义进行区分。

● 难点2：理解并掌握“＜”“＝”“＞”的含义，区分“＜”与“＞”。

● 难点3：准确掌握数字4、6、8、9的标准写法。

● 难点4：解决“开始数未知”“中间数未知”结构的加减法实际问题。

难点1源于单元学习目标2，同时对应学习重点1，关照学生在测验中表现出的“难以区分基数和序数”“在理解数的前后关系及其在序列中的位置上存在困难”的薄弱点；难点2源于单元学习目标3，同时对应学习重点2，兼顾以往教学中学生总会混淆“＜”“＞”两个符号开口方向的既有事实；难点3源于单元学习目标1和单元学习目标9，同时对应学习重点3，综合这四个数字相较于其他数字的书写难度及学生实际书写情况；难点4源于单元学习目标7，对应并高于学习重点4，通过整体考量这类问题的自身难度、学生在测验中表现出的困难以及过往的教育教学经验确定。

（三）对“0～9数的认识”模块学习重难点的把握

1.“0～9数的认识”模块学习重点

整体把握单元学习重点后，再依据单元知识结构，将其分解为若干模块学习重点（如表5）。其中，重点1归入A1的B1、B2；重点2归入A1的B4；重点3归入A2的B7；重点4归入A3的B8、B9、B10，且每个子模块都包含运算意义、运算方法两个方面的学习重点。

2.“0～9数的认识”模块学习难点

根据单元学习难点，设置模块学习难点（如表6）。其中，难点1归入A1的B2、B3；难点2归入A1的B4；难点3归入A2的B7；难点4归入A3的B8、B9、B10，且每个子模块都包含解决实际问题方面的学习难点。

整体把握“0～9数的认识”单元学习目标和重难点，是开展单元整体教学设计不可或缺的一环。这有助于教师在教学设计与实施过程中，有针对性地突出重点、攻破难点。

参考文献：

［1］徐文彬，陈韵娴，潘禹辰.小学数学“0～9数的认识”单元知识结构的确立（上）［J］.教学月刊·小学版（数学），2023（11）：9-11.

［2］徐文彬，陈韵娴，潘禹辰.小学数学“0～9数的认识”单元知识结构的确立（下）［J］.教学月刊·小学版（数学），2023（12）：9-14.

［3］徐文彬，陈韵娴，潘禹辰.小学数学“0～9数的认识”单元学习心理过程的建构［J］.教学月刊·小学版（数学），2024（5）：9-14.

［4］安德森.布卢姆教育目标分类学：分类学视野下的学与教及其测评［M］.蒋小平，译.北京：外语教学与研究出版社，2009.

*本文系全国教育科学“十三五”规划2018年度国家一般项目“中小学STEM教育基本理论与本土实践问题研究”（项目编号：BHA180126）的研究成果。