初中数学靶向情境建构的教学实践

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）明确提出，学生要通过数学学习获得适应未来生活和进一步发展所必需的基础知识、基本技能、基本思想和基本活动经验；同时，要让学生体会数学与生活之间的联系，在探索真实情境所蕴含的关系中，发现问题和提出问题，用数学和其他学科的知识与方法分析问题和解决问题。如何使数学教学更有效，笔者认为可以利用靶向情境的建构。靶向情境又称“整合情境”或“学业获得之重新投入的情境”，是指在学习过程中，教师设计的具有整合学业所得和评估这些所得功能的情境。一个有效的靶向情境能够实现知识的整合，激发学生利用所学知识与技能探究问题的动机，并帮助教师评估学生的学习效果。下面，笔者以微课“中位数和众数”的教学为例，谈谈具体的教学实践。

一、教学目标

理解中位数和众数的概念，能根据所给的信息求出一组数据的中位数和众数；结合具体情境理解平均数、中位数和众数的联系和区别，并能根据具体问题，选择合适的统计量表示数据的集中趋势；体验数学问题来源于生活，并用所学知识服务于生活。

二、创设理念

新课标指出，统计领域的学习是为了让学生通过数据认识世界的意义，同时感知大数据时代的特征，从而更好地发展数据观念和模型观念。结合教学目标，笔者尝试建构靶向情境链，思考：希望学生跨越什么样的障碍？应该设置什么样的背景？如何在“靶向”功能上予以开发利用问题情境？解决问题的意义是什么？通过思考以上问题，笔者创设了一个包含复杂问题的靶向教学情境，一方面引发学生的好奇心，激发学生的学习兴趣，让学生感知现实生活中的数据；另一方面让问题从情境中生成，引导学生通过有效学习，整合知识，解决情境中的问题，从而也达到检验学习成果的目的。

三、情境建构

1. 整合知识，提出问题

笔者设计了一个生活化的情境，贯穿教学活动始终。

明明在放学路上，听到三位家长的对话：

钟阿姨说：“这周末我想带孩子去上海游玩，你们有推荐的吗？”张叔叔说：“上海博物馆、上海科技馆、上海自然博物馆、上海电影博物馆，上海可以参观的博物馆有很多。”魏大爷说：“那怎么选呢？我也想带孙子出去转转。他参加了一个比赛的初赛，10个孩子里选出前4名参加复赛，初赛的平均分是70分，我孙子只考了68分，他觉得可能无法参加复赛，有些沮丧。”张叔叔羡慕地说：“能选拔参加初赛就已经很厉害了。最近我家孩子想骑自行车上学，我家离得远，骑车大约要1个小时，我考虑是否在学校附近租房。”如果你是明明，你能利用统计知识，帮助钟阿姨、魏大爷、张叔叔解决问题吗？

【设计意图】通过设计复杂情境，把平均数、中位数和众数知识融合到一组实际问题中。在学习本节课前，学生只学习了平均数，还无法解决问题。问题的提出激发了学生对新知的探索欲。

2. 教授新知，理解概念

笔者援引了一个案例：献爱心捐款活动中，某校九年级一班第三小组11名学生的捐款数（单位：元）：1，3，3，2，5，4，3，6，7，7，80。由数据可得出，平均捐款11元，但11并不能较好地反映这组数据的集中趋势。11名学生中，有10名学生的捐款数小于11元，只有1名的捐款数大于11元，80这个异常数据对平均数产生了影响。

【设计意图】使学生更好地理解原始情境，引出中位数和众数，明确平均数与它们的区别。

3. 解决问题，评估效果

回到最开始的复杂情境。钟阿姨去哪个博物馆参观？魏爷爷的孙子能不能进入复赛？张叔叔是否需要租房？请学生利用所学的平均数、中位数、众数的知识，小组合作交流，帮助三位家长解决问题。

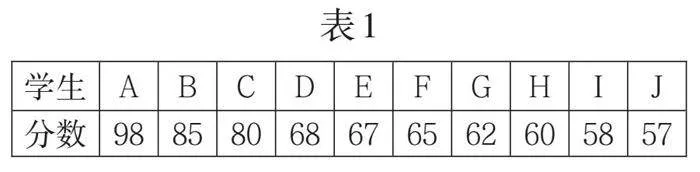
学生解决问题时，自然而然会把新旧知识进行整合。有的学生建议利用众数解决参观博物馆的问题，如搜出大众点评上的好评数量，好评次数最多的更值得去参观。对于魏爷爷的问题“平均分为70，68分能不能进前四”，学生通过计算，列出了表1，说明68分也有希望。

表1

[学生 A B C D E F G H I J 分数 98 85 80 68 67 65 62 60 58 57 ]

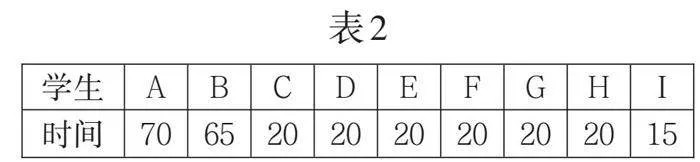
对于张叔叔的问题，有的学生建议整理同班学生骑车上学所需时间（单位：min），如表2，该平均时间是30分钟，但这组数据中有异常值，平均数并不能很好地反映平均水平，中位数20分钟更能反映这组数据的集中趋势，所以还需要参考20分钟这个实际情况来考虑是否租房。

表2

[学生 A B C D E F G H I 时间 70 65 20 20 20 20 20 20 15 ]

【设计意图】使学生能在真实情境中学会合理运用统计量分析问题。这一过程不仅凸显靶向情境的整合功能，而且评估学生的课堂学习效果，完善了课堂教学的评价体系。学生在情境中对学过的知识加以调动，能力得到提升。

四、教学反思

本节微课中，笔者联系实际生活，参照教学目标，构建了一个靶向情境。在教学过程中，设计的问题富有很大的挑战性，带给学生不少新鲜感，让他们主动以解决问题为目标投入学习，改变了传统的学习方式。靶向情境的建构过程中，教师的教学设计应当考虑教学的整条靶向情境链。这条情境链从学生和某个概念的最初本质出发，最后指向对这个概念的整合。为了进一步有效促进学生整合学业获得和发展能力，需要一线教师根据学科特点，立足现实，有针对性地尝试靶向情境的设计和开发，建构一个真正的靶向情境，即对学习有用的情境：激发学生动机的情境、可以实现的情境。这样才能给数学教学改革实践带来灵感和行动参照。

（作者单位：江苏省苏州中学伟长实验部）