积累活动经验 培养核心素养

网格作图是指借助网格中蕴含的数量关系（相等、倍分）与位置关系（平行、垂直），作出符合特定数量关系和位置关系的图形。网格是义务教育阶段研究“图形的性质”“图形的变化”和“图形与坐标”的重要工具，网格作图对学生的二维空间观念、模型建构能力和几何直观要求比较高，能很好地落实《义务教育数学课程标准（2022年版）》（以下简称“新课标”）对学生核心素养的培养要求。下面，笔者以2023年江苏省南京市鼓楼区九（上）期末试卷第23题的教学为例，谈一谈如何通过对网格作图题多样性解法的探究，着眼基础，积累活动经验，形成知识、方法、经验的生长链，培养核心素养。

一、试题呈现

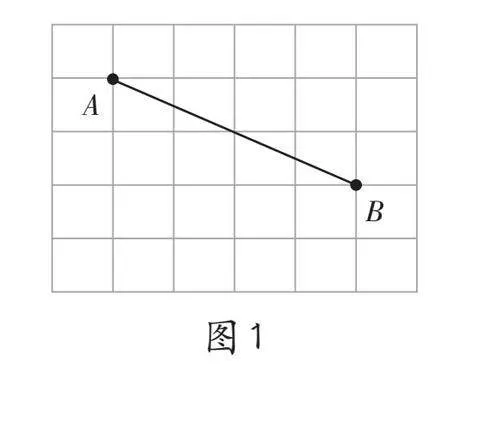
如图1，在5×6的网格上，线段AB端点都是格点，画出它的一个三等分点M。要求：1. 用两种不同方法作图；2. 画图工具仅限无刻度直尺。

二、教学分析

1. 寻找思路，转化问题

本题中，三等分点M并不是图中的格点，因此需要结合其他知识点寻找点M。学生根据所学知识，可由比例1[∶]3 ，想到“平行线分线段成比例”这一基本事实及其推论。角平分线定理和三角形的重心也涉及三等分点这一特殊数量关系，但由于角平分线定理在初中阶段不常见，这里不再对其展开叙述。

2. 明确方向，构图突破

问题1 能否通过“X型相似”，构造图形，寻找点M呢？

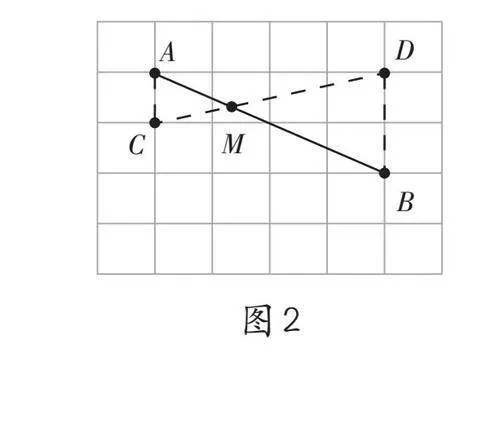
如果可以通过构造“X型相似”的基本图形来解决，就需要作除已知线段AB外的一条线段CD，使两条线段相交，并满足AC∥BD且[ACBD]=[12]。如何确定C、D两点呢？此时，可以引导学生利用网格，取格点C、D，如图2，连接AC、BD，则BD∥AC，连接CD，交AB于点M，则点M即为所求。

在这一解题思路中，C、D是两个不确定的点，可以看作两个变化的量，因此，可以引导学生考虑控制变量，即先确定一个点C的位置，从而可根据“平行且满足比例为1[∶]2的关系”确定点D的位置。理论上点C的位置有无数个，从而线段AC有无数种可能，由此也可得多种解法。

问题2 能通过构造“A型相似”来解决吗？

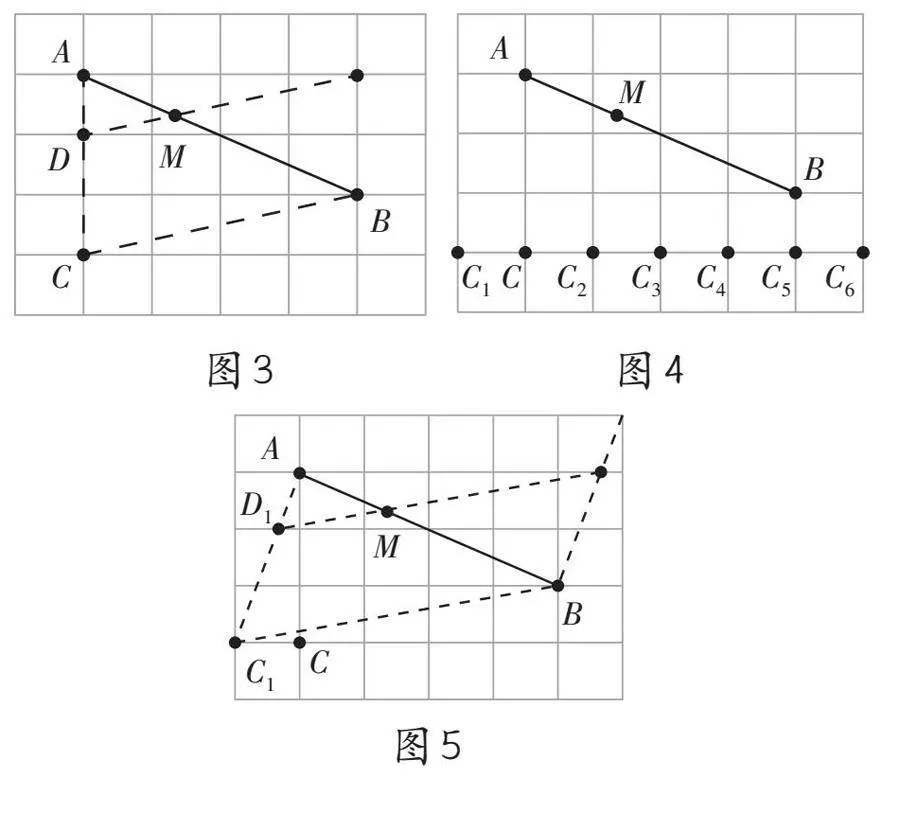
与“X型相似”类似，若要构造“A型相似”，则需要构造△ABC，再过AC边的三等分点作BC的平行线，该线与AB交于点M，则点M即为所求，如图3。解题的关键在于如何找AC的三等分点。还是引导学生考虑从特殊情况入手，如图3，取AC=3，则格点D恰为AC的一个三等分点，连接BC，过点D作DM[∥]BC，交AB于点M，点M即为所求。在此基础上，改变点C的位置，如图4，从而将点D一般化。例如选择点C1，如图5，连接AC1、BC1，在△ACC1中，可得D1为AC1的三等分点，再作D1M∥BC1，交AB于点M，则点M即为所求。同理，可以选择点C2、C3……

问题3 由三等分点可以想到重心的性质，你能借助重心的性质解决吗？

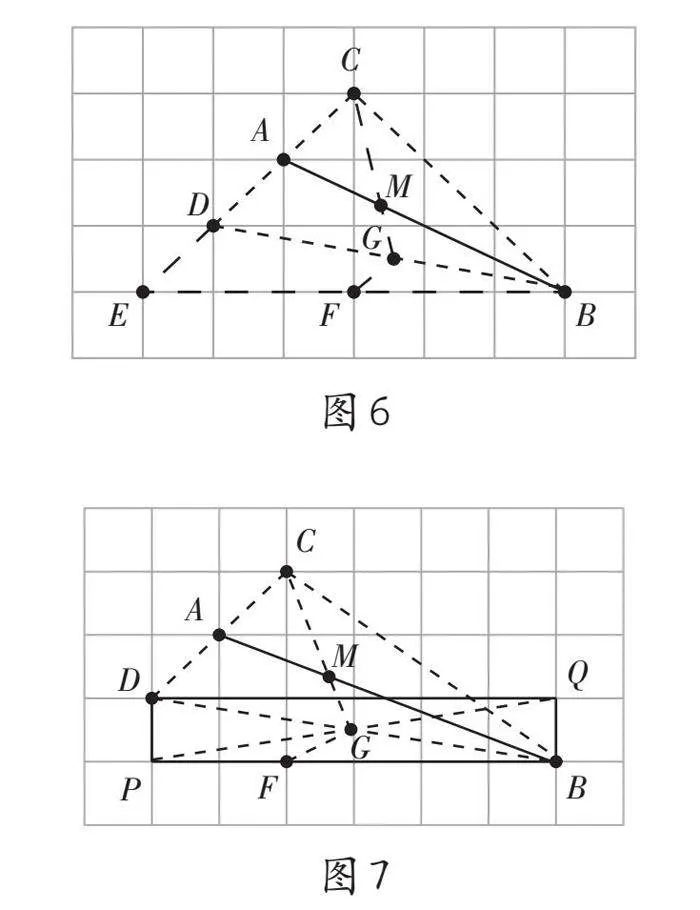
如图6，以点A为中点作线段CD，连接BD、BC，作BD的中线交AB于点M，则点M即为所求。由于三角形的重心分中线为1[∶]2两个部分，所以可以引导学生考虑将线段AB和点M分别看作某个三角形的中线和重心，由此考虑以点A为中点作一条线段，构造一个三角形，再找一条线段的中点，连接对应顶点后，与已知直线的交点即为三等分点。在此过程中，可以引导学生利用△DEB构造中位线（如图6），也可以借助网格，构造以BD为对角线的矩形DPBQ，找BD的中点（如图7）。

在网格中作出线段的n（n≥3）等分点或将已知线段分成m[∶]n（m、n为正整数）的两部分，皆可以运用相似的方法，利用“平行+线段”成比例，借助网格的特殊性构造“X型相似”或“A型相似”来完成。如果尺规作图要求作n等分点或分线段成比例，思路也大致相同，用圆规作等长线段和等角，构造出平行后，也就有了相似。

三、教学反思

1. 研读课标，解析核心素养的主旨性

新课标将数学核心素养表述为“会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界”。本题教学过程更多体现了推理能力、模型观念和几何直观的培养。几何能力核心素养体现在“根据语言描述画出相应的图形，分析图形的性质”。学生通过“X型相似”或“A型相似”模型，将抽象的数学问题直观化、具体化，同时在作图过程中，通过计算，分析数量关系及位置关系。教师在平时教学时要着力帮助学生有效积累活动经验，通过新授课、试题讲评课、复习课、综合与实践的教学，引导学生经历观察、猜测、实验、计算、推理、验证、数据分析、直观想象等数学学习过程，形成分析与解决问题的一般路径：特殊化→一般化→逆向思考→延伸发散，再通过转化、类比等数学思想，获得解决问题的一般策略和经验。

2. 立足教材，体现教学评一致性

新课标对数学教材素材选取的要求如下：为学生的数学学习活动提供了学习主题、知识结构和基本线索，是实现数学课程目标、实施数学教学的重要资源。关于平行线分线段成比例的教学，教师一般可以设置如下操作活动：（1）在练习本上，先画3条互相平行的直线l1、l2、l3，再任意画2条直线a、b，使a、b与l1、l2、l3分别相交于A、B、C和D、E、F。（2）度量所画图中AB、BC、DE、EF的长度，计算对应线段的比值。（3）你有什么发现？请与同学交流。（4）在练习本上，画4条、5条……互相平行的直线，重复上面的过程，你发现的结论还成立吗？该活动设置的意图，一方面是创设有效情境，让学生用数学的眼光去观察，将生活事物数学化；另一方面是从特殊到一般，引导学生用数学的思维去思考，形成探究数学问题的数学思维。新课标指出，坚持素养立意，凸显育人导向。以核心素养为导向的命题，要关注数学的本质，关注通性通法，综合考查“四基”“四能”与核心素养。开展有效体现教学评一致性的教学活动，需要教师立足教材，设计活动，将数学本质、通性通法贯穿整个教学过程：展现“知识背景→知识形成→揭示联系”过程；运用数学知识解决问题，适当体现“问题情境→建立模型→求解验证”过程，帮助学生有效理解知识与方法，积累活动经验，提高“四能”。本节课的题干中，命题者从三个角度对学生的学习过程进行考查和评价：一是考查学生对教材中定理的掌握程度和逆向使用的能力，即由“平行于三角形一边的直线与其他两边相交，所截得的三角形与原三角形相似”抽象出“A型相似”和“X型相似”；二是考查学生在课堂的学习过程是否真正经历“知识背景→知识形成→揭示联系”的过程；三是考查学生在课堂学习的过程中是否有效理解了知识与方法，是否积累了活动经验，这也促进教师主动改变教学策略，主动开展素养导向的教学，真正体现“以学生为主体，让学习真实地在课堂发生”。

（作者单位：江苏省南京求真中学）