基于Cornish-Fisher-VaR方法及t-GARCH模型的生猪期货套期保值研究

摘要：生猪期货作为一种新兴期货合约，其套期保值功能的实际效果以及套期保值比的测算需要深入研究。本文采用最小Cornish-Fisher-VaR方法和t-GARCH模型，对生猪期货的最优套期保值比进行了分析。研究结果显示，生猪期现货市场的价格波动相对较小，套期保值效果有进一步提升的空间；修正t-GARCH-VaR套期保值方法在不同置信水平下提供了灵活的套期保值比，更符合实际套期保值决策，并通过对套保组合绩效的分析，验证了修正t-GARCH-VaR套期保值方法的有效性。最后，针对生猪期货的套期保值，提出了进一步完善的建议。

关键词：生猪期货；套期保值；VaR；t-GARCH；Cornish-Fisher

一、引言

2021年1月8日，我国首个活体期货合约——生猪期货在大商所成功上市，此后一直受到各界广泛关注。截至完稿日，生猪期货已稳定运行2年有余，期货价格和现货价格逐渐形成联动关系，表现出逐渐增强的态势，这为生猪相关企业利用该期货进行套期保值提供了契机，使他们能够通过这一期货合约来对冲现货市场的价格大幅波动，那么当前生猪期货是否已较好发挥套期保值功能，需要进一步评估、探讨。此外，生猪期货是大额合约，需要投资者支付较高的保证金，且期货价格较现货具有更强的波动性，这就要求期货的套期保值能够反映投资者的风险容忍程度。同时，在进行生猪期货的套期保值时，需要深入了解期货与现货之间的基差变化，

并运用计量分析等方法达到预期的套期保值效果。

二、文献综述

期货市场是金融市场的一个重要组成部分，主要通过套期保值策略来转移风险。套期保值的核心问题在于确定最佳的套期保值比。传统的完全套期保值策略要求套期保值比为1，即持有的期现货数量相等。但由于存在基差风险，期货价格和现货价格走势并不完全相同，因此套期保值比为1的策略可能并不是最佳选择。

随着相关理论的不断完善，套期保值比的确定方法主要有三种：最小方差法、最大效用法、最小VaR法。对于最小方差法，迟国泰等（2008）在最小方差套期保值模型下，利用多元GARCH对多品种期货套期保值决策模型进行了实证分析。王佳等（2020）构建三种最小方差套保模型，并与完全套期保值以及无套期保值的沪深300指数现货的绩效进行了对比。这种方法的缺陷在于以风险最小化为目的获得套期保值比，而未考虑投资收益，且最小方差法不能反映投资者风险偏好。对于最大效用法，虽然同时考虑了投资收益和风险，但其套期保值比的计算需要知道投资者的效用函数，且对于不同的投资者来说，其效用函数是不相同的，因此在实际使用中并不常见。对于最小VaR方法，由于其综合了套保组合的收益率和风险，同时借助置信水平来反映投资者的风险偏好，是当前获得套期保值比的一种主流方法。徐荣等（2016）以最小VaR为目标，分别使用GARCH、EWMA模型测算期现货波动率，考虑到对套保组合收益率正态性假设不足，运用Cornish-Fisher方程对高斯分布的分位数进行了修正，结果表明对沪深300股指期货的套期保值效果较好。曹志鹏和路华（2018）构建最小VaR套保模型，并利用GARCH模型计算套期保值比中的方差、协方差，以境外人民币为研究工具对模型进行实证分析，结果表明最小VaR方法较最小方差法无论是在套保效率上，还是成本上都更优。梁艳（2020）使用非对称类GARCH模型测算VaR方法下的套期保值比，研究结果显示，这种策略在满足VaR约束的同时，能够实现更高的套保组合累计收益率，同时减少套保交易成本。

在对套期保值的收益率波动预测方面，研究表明在围绕GARCH族模型，测算方法呈现交叉、多元的发展趋势。部分学者尝试使用EWMA、GARCH模型对期现货的方差进行预测，解决了在历史期和套期保值期间因收益率波动发生结构性变化所导致的套期保值效果失真的问题。也有不少学者通过构建多元GARCH（DCC-GARCH）模型对期现货的波动率进行预测，测算动态套期保值率。对这部分研究缺陷主要表现在以下两点。第一，相对于简单模型，复杂（或高级）模型具有较小的模型（误设）风险，但由于包含更多的变量和参数，模型的估计风险也相对较大。因此，无法确定复杂模型的整体表现一定优于简单模型。并且，过度追求复杂模型可能使研究偏离了为市场提供服务的初衷。第二，对于GARCH模型本身的设定上，多数研究是在假定高斯分布下构建GARCH模型，而实际情况是，资产收益率序列往往具有尖峰厚尾特性，这会导致对资产的波动预测不够精准。因此，有必要选用t分布作为收益率的随机分布进行模型分析，以考虑其尖峰厚尾特性。

生猪期货作为一种新型期货品种，当前对生猪期货套期保值的研究仍停留在对制度、对策的定性分析上，对生猪期货使用套期保值模型进行定量实证分析的研究不多。综上所述，本文拟在最小VaR方法下，利用t分布下构建GARCH模型对期现货的标准差进行预测，测算生猪套保组合的最优套期比率。同时，为了进一步提高VaR方法下测算套期比的准确性，使用Cornish-Fisher方法对高斯分布分位数进行修正，得到修正后的最优套期比率。最后对套期比率的有效性进行检验，并为我国生猪期货的套期保值提供合理化意见。

三、理论模型介绍

（一）基于VaR方法的套期保值模型

Johnson在均值-方差模型的基础上，提出了在方差最小化条件下的最优套期保值比。考虑1个套期保值组合由1单位的生猪现货，以及为了对冲风险持有的h单位的生猪期货空头组成。Ft、St分别表示期现货的价格，那么Rf=（Ft－Ft－1）/Ft-1表示期货的收益率、Rs=（St－St－1）/St-1表示现货的收益率，则套期保值组合的收益率Rh可表示为

Rh=（CsStRs－CfFtRf）/CsSt=Rs－hRf（1）

其中，h代表套期保值比。若σ2f、σ2s分别为期现货收益率的方差，σfs为期货和现货收益率的协方差，套保组合的方差σ2h可表示为

σ2h=σ2s+h2σ2f－2hσfs（2）

此时若以σ2h来衡量套保组合的风险，并通过对式（2）最小化目标函数，可得到最小方差法下的最优套期保值比：

h*MV=σfs/σ2f=ρσs/σf（3）

其中，ρ为期货和现货收益率的相关系数。

由于最小方差下的最优套期保值比未考虑投资收益且不能反映投资者的风险偏好，根据上述内容引入最小VaR方法下的最优套期保值比。风险价值VaR可表示为套期保值组合收益率Rh在一定置信水平α下，在未来一段时间内的最大可能损失：

Prob（Rh≤－VaR（h））=1－α（4）

在VaR方法下，套期保值比的确定是通过最小化每个套期保值比对应的VaR值，进而得到最佳的套期保值比。考虑在方差-协方差法（正态分布法）下计算VaR值，通过中心极限定理标准化式（4），并作等式变换，可得到VaR目标函数表达式：

VaR（h）=－E（Rh）+Φ－1（α）σh（5）

其中，E（Rh）表示套期保值组合收益率的期望，Φ－1（α）表示标准正态分布分位数。

对式（5）以套期保值比h为变量，求其满足一阶导为0、二阶导大于0的根，可得VaR方法下的最优套期保值比：

h*VaR=ρσsσf－E（Rf）σsσf×1－ρ2（Φ－1（α））2σ2f－（E（Rf））2（6）

观察式（6），不难发现VaR方法下的最优套期保值比由两部分组成，减号前的部分为纯套期保值部分，即最小方差下的最优套期保值比，主要强调投资者采取套期保值策略来应对市场实际价格风险，但并未体现投资者的风险偏好。减号后面为投机需求部分，主要表现为套期保值者对套期保值策略的风险偏好，实际上是在进行期货投机，并随着置信水平α的提高，投资人对风险的厌恶程度增大。

由于VaR方法下的最优套期比是假定套保组合收益率服从高斯分布得到的，而实际情况是资产收益率往往具有尖峰厚尾特性，实际分布不服从高斯分布。因此，采用Cornish-Fisher方法对标准正态分布分位数Φ－1（α）进行修正：

Φ－1（α）*=Φ－1（α）+16（［Φ－1（α）］2－1）ρ3+

124（［Φ－1（α）］3－3Φ－1（α））ρ4－136（2［Φ－1（α）］3－5Φ－1（α））ρ23（7）

这里，修正分位数Φ－1（α）*通过计算套保组合收益率Rh的偏度ρ3和峰度ρ4来得到。

（二）ARMA-GARCH模型

通常情况下，资产收益率序列往往具有尖峰厚尾特性，并伴随着一定的自相关和条件异方差性，为消除这些特性，可采用ARMA模型修正自相关，GARCH模型修正条件异方差。下式给出了ARMA（p，q）-GARCH（m，n）的一般形式：

rt=c+∑pi=1αirt－i+∑qj=1βjet－j+et（8）

et=σtvt（9）

σ2t=ω+∑mi=1φie2t－i+∑nj=1θiσ2t－j（10）

式（8）为均值方程，刻画ARMA（p，q）过程，t代表时间，r表示收益率，c代表均值方程的截距项，et代表残差序列，αi为自回归项系数，表示滞后i期的收益率对当前收益率的影响，β为移动平均项系数，表示滞后j期的残差对当前收益率的影响。式（9）描述了残差项，σt为条件方差，vt为服从自由度为v的标准t分布。式（10）为方差方程，ω为常数项，φ、θ分别表示ARCH系数和GARCH系数。

通过GARCH模型估计期现货的条件方差代入式（6），可得到最小VaR方法下的动态套期保值比。

（三）套期保值比有效性检验指标

采用风险降低比例（He）来对套期保值比的有效性进行检验。其方法是根据方差标准来衡量进行套期保值后相对未进行套期保值时的风险减少程度。公式表示为

He=σ2u－σ2hσ2u=1－σ2hσ2u（11）

其中，σ2u表示未进行套期保值（即现货）的收益率的方差。风险降低比例He越大，说明该套期保值比对风险减少的越多，套期保值效果越好。

四、实证分析

（一）数据选取及描述性统计分析

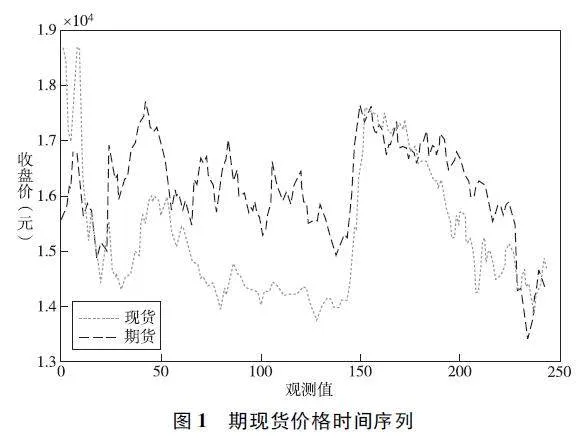
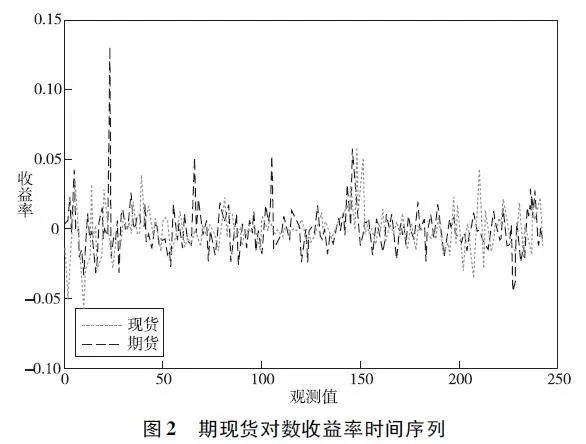
本文选取大连商品交易所2022年12月19日至2023年12月18日生猪期货主力连续合约的每日收盘价作为期货价格时间序列。对于生猪现货，考虑到不同地区的生猪价格不一致，本文选取2022年12月19日至2023年12月18日外三元生猪全国平均价格作为现货价格时间序列。以上数据来源于大商所交易网以及中国养猪网。在剔除期现货交易日不对应、缺失数据后，最终得到135组期现货价格数据，如图1所示。可以看到，生猪期货价格与生猪现货价格走势呈现一定的联动关系，这也印证了期货市场具有一定的价格发现功能。

时收益率伴随着一定的波动聚集性，即大波动后紧跟着大波动，小波动后紧跟着小波动，吻合波动率模型建模特征。

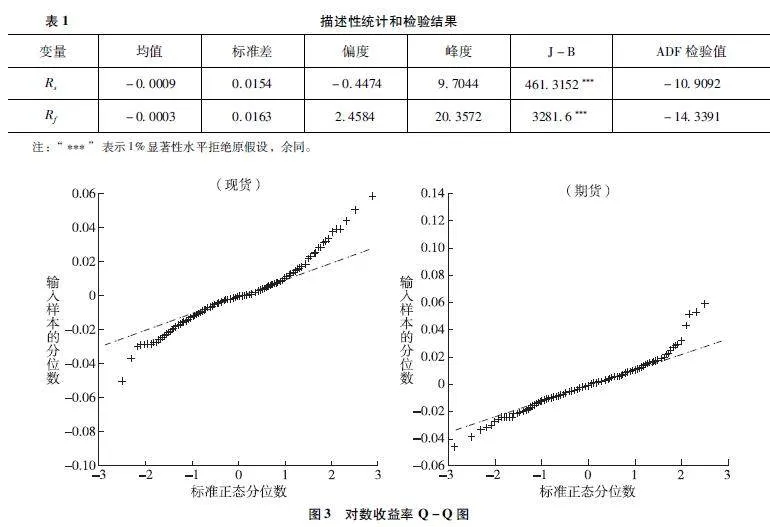
对该收益率序列的统计特性、相关检验进行进一步分析，结果如表1所示。从均值计算结果来看，期货的收益率均值为负值，这表明当前投资者在生猪期货市场上获得的平均收益低于现货市场。另外，生猪期现货的收益率标准差均很小，表明当前生猪市场的收益波动较小，那么套期保值的效果可能受到削弱。现货偏度系数大于0，属于右偏分布，期货偏度系数小于0，属于左偏分布，说明收益率序列是非对称的。峰度系数均大于高斯分布的峰值3，同时J-B检验结果在1%显著性水平下能够认为序列不服从高斯分布。结合对数收益率序列Q-Q图（见图3）可知，尾部样本点明显偏离直线，说明收益率分布函数尾部相较于高斯分布尾部具有厚尾特性。最后，对收益率序列做平稳性检验可知，ADF检验t统计量在5%显著性水平下接受原假设，即该序列平稳，可对序列继续进行GARCH建模分析。

（二）ARMA-t-GARCH模型构建及样本过滤

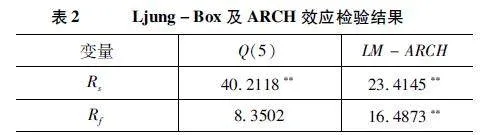
对收益率序列进行GARCH建模前，需要先对序列的自相关性及异方差特性进行检验（结果如表2所示）。对生猪期货、现货收益率分别做滞后5阶的Ljung-Box检验结果表明，现货收益率序列存在自相关性，而期货收益率序列不存在自相关性，这可能是由于期货市场交易具有高度标准化和透明度的特点，导致期货市场价格波动更加及时，从而减少了序列的自相关性。拉格朗日乘数LM-ARCH检验结果表明，期现货收益率序列均存在异方差特性，可以构建GARCH模型。

变量Q（5）LM－ARCH

Rs402118**234145**

Rf83502164873**

注：Q（5）代表对序列做滞后5阶的Ljung-Box检验；“**”表示在5%显著性水平拒绝原假设，余同。

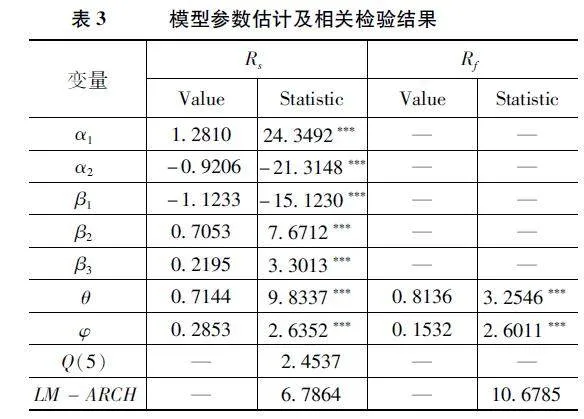
因此，对于生猪现货收益率序列还需要先构建ARMA模型消除序列自相关性，模型阶数由自相关、偏自相关函数及结合AIC、BIC信息准则确定，最终选择构建ARMA（0，1）模型作为均值方程。对于GARCH模型，其定阶比较困难，不少研究表明滞后阶数取值都为1的GARCH模型，一方面具有很好的拟合性；另一方面在金融上的应用更为广泛，而且也符合计量模型简约性的要求。t-GARCH模型估计结果如表3所示，参数估计结果均在1%显著性水平下显著，且序列已不存在自相关性和ARCH效应。

（三）套期保值比测算

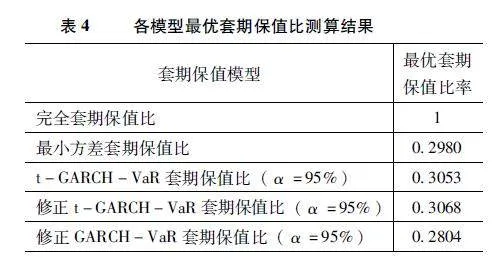
根据t-GARCH模型估计得到的条件方差σs，t、σf，t，并将收益率序列相关统计参数分别代入式（3）、式（6），可得到最小方差方法及最小VaR方法下的动态最优套期保值比。考虑到最小VaR方法下的最优套期保值比计算公式是在高斯分布假设下推导而来，将最小VaR方法下修正前的套期保值组合收益率Rh的偏度ρ3和峰度ρ4代入式（7），对标准正态分布分位数修正得到Φ－1（α）*，并重新代入式（6）测算其最优套期保值比。为方便对比论证，同时采用基于高斯分布的GARCH模型，测算最小VaR方法下修正后的动态最优套期保值比。以上动态最优套期保值比测算结果均取其均值，如表4所示。

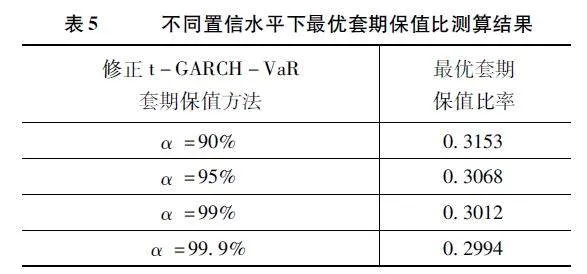
由于在最小VaR方法下的最优套期保值比可根据设置不同的置信水平α来体现套保人的风险偏好，因此本文继续在修正t-GARCH-VaR方法下对置信水平分别为90%、95%、99%、999%下测算最优套期保值比，结果如表5所示。可知，随着α增大，套保者对风险容忍程度变小，最小VaR方法下最优套期保值比的投机部分的作用变弱，而越来越接近最小方差方法下的最优套期保值比，因此最小方差下的最优套期比实际上是最小VaR法下最优套期比的一种特例。

（四）套期保值效果分析

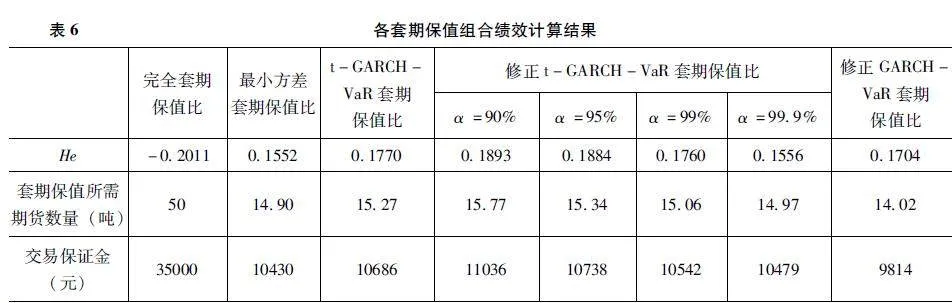
利用式（11）对各套保组合的风险降低比例进行计算，同时假设现有生猪现货50吨，生猪期货价格14000元/吨，为规避生猪价格下跌带来的风险，展开空头套保，交易保证金比例为5%，各套期保值组合效果的量化结果如表6所示。

首先可以看出，完全套保方法下He为负数，意味着套期保值后的收益方差比套期保值前的收益方差还要大，这表明套期保值并没有有效地降低价格波动带来的风险，反而可能增加了风险。因此，在进行生猪期货套期保值过程中，要意识到生猪期现货基差存在的风险，不宜采用完全套期保值理论下的等比例套期保值。在95%置信水平下，修正后t-GARCH-VaR模型套期保值效果比修正前套期保值效果有了提升，同时较修正后的标准GARCH-VaR套期保值效果也有了提升，这说明通过t-GARCH模型及Cornish-Fisher方法能够改善在假设生猪套保组合收益率服从高斯分布情形下的套期保值效果。各个置信水平下，修正t-GARCH-VaR套期保值效果均要优于最小方差法，且随着置信水平的提高，修正t-GARCH-VaR套期保值效果与最小方差套期保值效果越来越接近。总体来看，修正t-GARCH-VaR套期保值方法在90%置信水平下套期保值效果最好，即50吨的生猪现货需要1577吨的生猪期货对冲风险，风险降低比例与未做套期保值相比下降了约19%。较低置信水平（90%、95%）与较高置信水平（99%、999%）相比，较低置信水平下允许的风险敞口变大，进行套期保值时可供对冲的风险增多，在实际操作中还是要根据套保人的风险偏好程度调整参数，灵活地运用于套期保值决策中。

五、结语

当前，生猪期货的套期保值效果相对其他农产品期货（如大豆、棉花等）的套期保值效果仍然偏低，一方面这可能是由于我国生猪期货上市时间尚短，市场发展仍然不成熟，导致生猪期货与现货市场之间的相关度较低而错过一些价格波动的机会，影响了套期保值的效果。另一方面，生猪期货市场的交易量和流动性还处于一个较低水平，参与套期保值的主体数量有限，高交易门槛使得资金较少的投资者难以进入市场，进一步限制了交易量和流动性，而这对于期货市场的发展至关重要。

根据本文研究，可以从以下几点入手改善：第一，完善套期保值工具。推动生猪期货市场的发展，降低交易成本，提高套期保值工具的效率和灵活性，以便更好地满足套期保值需求。第二，提高市场透明度。加强市场监管，提高市场透明度，减少信息不对称，为套期保值提供更为稳定和可靠的市场环境。第三，提供政策支持。政府可以出台支持生猪产业的政策，以确保市场稳定，但也要根据市场实际情况灵活调整政策，以避免过度干预导致市场僵化和不健康发展。第四，加强市场推广。开展生猪期货市场的推广工作，吸引更多的养殖企业和相关行业参与者进入市场，增加市场的流动性和活跃度。通过市场推广，可以提高套期保值工具的使用率，促进市场功能的完善。

参考文献

［1］王梦圆，陶红军我国生猪期货发展现状、机遇及挑战［J］中国猪业，2023，18（5）：17-20，25

［2］张海峰，黄锦烨，周自阳，等我国生猪期货市场发展现状与趋势分析［J］中国猪业，2023，18（5）：13-16

［3］王佳，何柳杨，王旭基于EMD-DCC-GARCH的沪深300股指期货多尺度动态套期保值研究［J］运筹与管理，2023，32（9）：200-207

［4］迟国泰，杨万武，王玉刚基于资金限制的多品种期货套期保值决策模型［J］系统工程理论与实践，2008（6）：1-13，58

［5］王佳，金秀，王旭，等基于时变Markov的DCC-GARCH模型最小风险套期保值研究［J］中国管理科学，2020，28（10）：13-23

［6］迟国泰，余方平，刘轶芳基于VaR的期货最优套期保值模型及应用研究［J］系统工程学报，2008，23（4）：417-423

［7］李胜婷玉米期货动态套保及绩效评估研究——基于VaR-GARCH模型［D］大连：东北财经大学，2020

［8］徐荣，李星野，马静应用EWMA-GARCH（1，1）-M模型对沪深300股指期货最小VaR套期保值效果研究［J］经济数学，2016，33（4）：69-74

［9］曹志鹏，路华基于GARCH-VaR方法的套期保值比与效率的实证［J］统计与决策，2018，34（16）：157-160

［10］梁艳螺纹钢期货套期保值方法创新与应用研究——基于GJR-GARCH-VaR模型的分析［J］价格理论与实践，2020（8）：108-111

［11］王玉刚，迟国泰，吴珊珊基于非线性相关的最小方差套期保值比研究［J］价值工程，2006（10）：154-157

［12］王玉刚，迟国泰，杨万武基于Copula的最小方差套期保值比［J］系统工程理论与实践，2009，29（8）：1-10

［13］皮天雷，游承静加密货币与传统金融资产市场的动态相关性研究——基于t-Copula-DCC-GARCH的实证分析［J］金融论坛，2022，27（5）：42-51

［14］周开国，关子桓欧盟碳排放交易体系运行效率研究——基于动态套期保值及价格发现的证据［J］国际金融研究，2023（2）：73-85

［15］付剑茹，袁倩莹，张伟期货套期保值模型选择：基于模型（误设）风险与估计风险视角［J］经济数学，2020，37（4）：38-46

［16］姚定俊，张路，程恭品“保险+期货”的套期保值比和绩效评估研究——以黄玉米为例［J］金融理论与实践，2022（5）：10-18

［17］王朋吾基于非对称GARCH类模型的中国股价波动研究［J］统计与决策，2020，36（22）：152-155

［18］JOHNSONLLThetheoryofhedgingandspeculationincommodityfutures［J］The ReviewofEconomicStudies，1960，27（3）：139-151

［19］AKGIRAYVConditionalheteroscedasticityintimeseriesofstockreturns：evidenceandforecasts［J］TheJournalofBusiness，1989，62（1）：55-80

［20］ENGLERF，NGVKMeasuringandtestingtheimpactofnewsonvolatility［J］JFinance，1993，48（5）：1749-1778

ResearchonLivePigFuturesHedgingBasedonCornish-Fisher-VaRMethodandt-GARCHModel

CHENGuodongWANGJiaqi

（SchoolofManagementandEconomics，NorthChinaUniversityofWaterResourcesandElectricPower，Zhengzhou450000，China）

Abstract：Asanewtypeoffuturescontract，thepracticaleffectivenessofhedgingandthecalculationofhedgingratioforhogfuturesrequirein-depthresearchThisstudyanalyzestheoptimalhedgingratioofhogfuturesusingtheminimumCornish-Fisher-VaRmethodandt-GARCHmodelTheresultsshowthatthepricefluctuationinthehogfuturesmarketisrelativelysmall，leavingroomforfurtherimprovementinhedgingeffectivenessThemodifiedt-GARCH-VaRhedgingmethodprovidesflexiblehedgingratiosatdifferentconfidencelevels，aligningmorewithpracticalhedgingdecisionsTheeffectivenessofthemodifiedt-GARCH-VaRhedgingmethodisverifiedthroughtheanalysisofhedgingportfolioperformanceFinally，furtherrecommendationsforhedginghogfuturesareproposed

Keywords：HogFutures；Hedging；VaR；t-GARCH；Cornish-Fisher