创融寻度，让空间思维可视

［摘 要］单元内整合不是简单的内容叠加，也不是同类的归并，而是要以学生的思维为核心，通过内容结构相仿的有效整合、思想方法迁移的有效融合、思维拓展提升的有效衍生来进行整体架构。

［关键词］单元整合；思维可视；三角形

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）17-0048-03

单元内整合拓展，是目前数学教师钻研的方向，其以连续、完整的视角分析、解构单元知识内涵，打通单元内部学习的“隔断墙”。然而，教师在操作中存在把整合看成简单的内容叠加或是同类归并的现象。笔者认为，要以学生的思维为核心，为学科知识与学生立场寻找教学支点。

笔者以人教版教材四年级下册“三角形”单元的教学为例探讨基于单元整体教学的整合构思与实践。

一、教材分析：摸排学情，找准起点

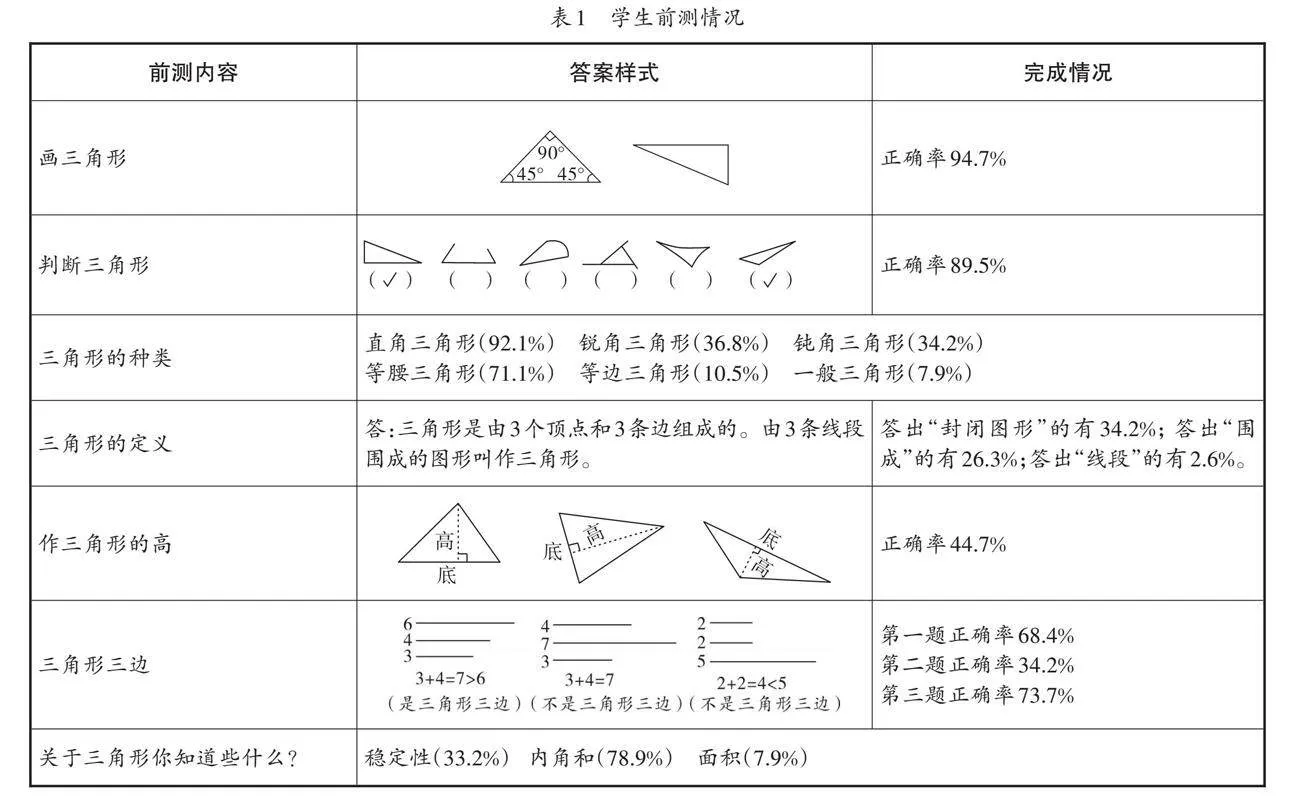
本单元属于图形与几何领域，包括图形的认识、测量、运动、位置等四个方面。学生通过对图形的认识和理解，发展空间观念和推理能力。在教学本单元之前，学生已经具备了一定的平面图形的知识基础，能从“边”“角”两个维度对平面图形进行研究，于是笔者对学生进行了一次单元性的前测。从前测结果（见表1）看来，学生对三角形的认识比笔者预想的要丰富，但涉及定义、说理或是证明的问题时，两极分化比较严重，学生对“角”的认识比“边”更充分，例如，认识“内角和”的学生远多于认识“三角形的定义”的学生，学生对“三角形的三边关系”是最陌生的。

二、单元设计：深挖内核，探寻融合点

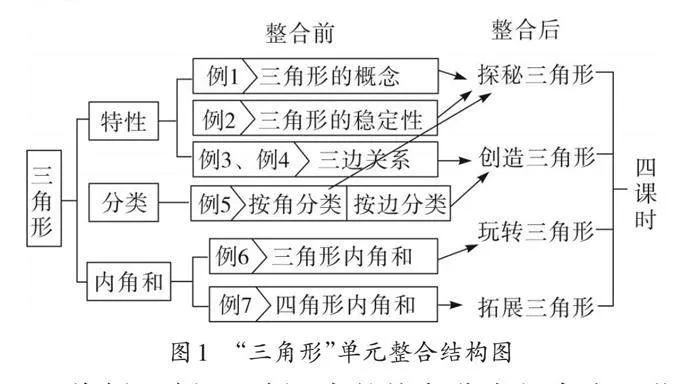
本单元教材从特性、分类、内角和三个方面让学生认识三角形。笔者依据教材特点和学生前测基础，基于整合思路，对“三角形”单元整体教学进行调整（如图1），将与内核结构相连的知识点相融重整。

将例1、例2和例5中的按角分类整合为一节“探秘三角形”全景扫描开启课，对三角形进行一次全面的认识，且突破画高的难点，促进学生对高有更完整的掌握。将例3、例4和例5中的按边分类整合为“创造三角形”镜头特写关键课， 从“边”和“角”两个维度深入研究三角形。将例6设计为“玩转三角形”双景推进关联课，打通“边”与“角”的关系。将例7设计为“拓展三角形”动态呈现拓展课，让学生了解三角形的外角。这四种课型，在单元基本结构的基础上分解难度，让内容逐级递增、螺旋上升。

三、实践探索：构建支架，增量思维

学习“三角形”必然要先从“认识三角形”开始，也就是本单元的开启课。而图形的认识一般从两个角度来思考：从教材体系分析，高是后续学习三角形的面积、梯形的面积，以及初中学习全等三角形、相似三角形等知识的重要基础；从学情角度来看，通过前测发现，学生学习三角形高的概念和画法时存在一定难度。因此，在开启课“探秘三角形”中，教师可以通过“三角形分类前置”“高线可视”“空间创想”等层层递进的环节，帮助学生分解难点，构建空间观念。

（一）分类前置——唤醒思维“点”

1.三角形的特征

基于学情特点和前测结果，在“认识三角形”的环节中，笔者唤醒学生对三角形表层的认识，凸显三角形的特点，从而完善概念教学。

【教学片段】

师（直接导入）：今天我们学习三角形。请你观察并说一说三角形有什么特点。

生1：由3条线段围成的图形叫作三角形。

生2：三角形有3条边、3个角和3个顶点。

生3：我为三角形各部分标上名称（图略）。

2.三角形的分类

教材将“三角形的按角分类”放在了“三角形的三边关系”之后，但为了更好地突破三角形高的教学难点，让学生系统地掌握高的定义和画法，笔者特意将“按角分类”与“认识三角形”进行整合，让学生能更系统、更完整地学习高，避免思维脱节。

【教学片段】

师（出示一个锐角三角形）：黑板上这个三角形的三个角都是什么角？

生1：三个角都是锐角。

师（质疑）：任何三角形都是有3个锐角吗？大家动手操作，画一画自己心目中的三角形。

（教师帮助学生将抽象概念具体化，将学生画的三角形拍照上传到屏幕上，让学生充分观察。）

师：你如何对三角形进行分类？有没有三角形中有多个直角或者多个钝角？说说你的想法。

（教师用课件演示）

师：由此我们可以知道三角形按角分可以分为什么？

生（齐）：锐角三角形、直角三角形和钝角三角形。

3.三角形的特性

三角形的稳定性是学生认识三角形的一个困惑点。教师可以用小棒搭一个三角形引导学生进行探究，从而让学生得出“用确定的3条边构成的三角形是唯一的”这一结论，并发现三角形具有稳定性。

【教学片段】

师：刚才我们通过画一画认识了三角形，并按照角对三角形进行了分类。现在我们进一步认识三角形。（出示图2）请你用这样的3根小棒搭一个三角形。

师：你们搭的三角形一样吗？你怎么证明呢？

（教师将几个学生搭的三角形串在一起（如图3），串在一起的所有三角形都完全重合，说明这些三角形是同一个三角形。）

师：确定的3条边构成的三角形是唯一的。

（教师让学生自己动手拉动手中的三角形，发现三角形具有稳定性。）

（二）高线可视——创设思维“链”

高是本节课的重点以及学生理解的难点，笔者将分三个层次进行教学，帮助学生建立高的概念。

1.识高：经验转化

怎样将已有的对平行四边形、梯形的高的认识转化为对三角形的高的认识呢？教师可以用刚才学生搭的三角形所摆位置的高低不同来突破对高的认识。

【教学片段】

师：通过图3，大家发现这些三角形是同一个三角形，这同一个三角形中还藏着什么奥秘？把同一个三角形按不同方向放在黑板上（如图4），你发现了什么呢？

生1：这3个三角形的高低不一样，中间的最高。

师：那这个三角形到底有多高呢？（动手指）大家量一量。

2.画高：本质转化

教师借助课件演示画高的规范操作，即“合—移—画—标”，学生掌握高的画法后自主画高，进一步巩固高的画法。

【教学片段】

师（示范画高）：画高的四个步骤是“合—移—画—标”。现在请一名同学按步骤在黑板上画高，其他同学试着在草稿纸上画一画三角形的高。

（学生画高）

师：大家在小组内说一说画高的过程。

3.拓高：思想转化

教师借助课件演示，将按不同方向摆放的三角形旋转重合为一个三角形（如图5），引导学生认识到同一个三角形有3组对应的底和高，并落实高的画法，让学生初步感知三角形的高有3条。

【教学片段】

师：刚才我们研究了锐角三角形有3条高，关于三角形的高，你还有什么问题吗？是不是任何三角形都有3条底和3条高呢？

（教师让学生自己对直角三角形和钝角三角形进行探究。）

（三）空间创想——生成思维“场”

在学生经历探究后，教师可以跟进三个梯度的练习。第一梯度的练习是通过三角形稳定性在生活中的应用，考查学生是否掌握了三角形的稳定性，在练习中提升学生的推理能力。第二梯度的练习“隐藏”三角形其中两个角，让学生判断三角形的类型，主要考查学生是否掌握了三角形的分类、是否能灵活地运用知识。第三梯度的练习是通过呈现一个已知底的三角形，先让学生在没有外界助力的情况下充分想象三角形的3条高会在哪里，随后通过“指一指”和“选一选”环节让学生找出三角形各底对应的高，接着在“猜一猜”环节中，画出2条高，让学生通过深入观察，预测第三条高会经过前2条高的交点，最后用几何画板演示，让学生直观感受任何三角形的高都能相交于一点。这三个梯度的练习不仅考查了学生的知识能力，还有意识地培养了学生的空间观念与动手操作能力。

总之，对于“三角形”的内容，要让空间思维真正可视。期待更多的教师能关注这一知识内容，探索出更成熟、更有效的教学之路。

［ 参 考 文 献 ］

[1] 侯学萍，陈琳.小学数学单元教学的整体设计[J].教学与管理，2018（29）：43-45.

[2] 席爱勇，吴玉国.基于结构化视角的单元整体设计路径[J].基础教育课程，2019（9）：35-39.

[3] 姚荣金.例谈小学数学学科内课程整合的实施策略[J].教学月刊小学版（数学），2017（11）：39-41.

（责编 杨偲培）