让“具身学习”为量感培养注入活力

［摘 要］量感是小学数学核心素养之一，小学阶段是培养和发展学生量感的关键时期。在实际教学中，教师应引导学生认识量的意义，从必要性、准确性、生成性、层次性和结构性五个方面考虑量感的培养策略。只有将量感的培养融入学生的具身学习，才能让学生通过亲身体验物体的量来感受量的意义，进而培养量感。

［关键词］量感；具身学习；度量

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）17-0085-03

《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）中提出，核心素养包括数感、量感、符号意识、运算能力等11种主要表现。其中，量感是新增加的一个核心素养。量感是一种直观感知，是在不使用测量工具的情况下对事物的可测量属性的直观感知。量感也是一种直觉，是会对真实情境选择合适的度量单位进行度量的直觉。量感还是一种感性认知，是对事物的大小、轻重、速度等可测量属性的感性认知。量感的形成基于大量的操作体验、经验的积累、理性的反思。可是，有部分教师在教学中对计量单位含义的讲解浮于表面，导致学生难以对量有准确的感知；有部分教师没有遵循学生的认知规律，导致学生机械记忆，在做单位换算的题目时容易出错；还有部分教师没有为学生提供足够的体验空间，使得学生估测的结果“谬以千里”，这些教学方式都对学生量感的建立造成影响。小学阶段是培养学生量感的关键期，笔者在实际教学中，探索具身认知理念指导下的量感培养策略，将量感的培养融入教学活动，引导学生认识量的意义。

一、在矛盾冲突中感知统一度量的必要性

度量又称测量或计量，是对事物的某个可测量属性（也称物理量）的估计或测定，估计或测定的结果必须用某一标准或度量衡来表示，表示结果中既有数字，又有计量单位，即数字加单位。通俗来讲，度量是指用标准的度量单位刻画物体的某个属性。在度量的发展史中，最初人们依赖于“身体尺”，也就是身体的某些部位，如一庹、一拃、一脚等。从最初的“身体尺”到如今各种精细的测量工具的发展过程是漫长的，测量工具由多元变成统一、由粗放变成精细。因此，在实际教学中，教师要善于创设适当的情境，引发学生认知上的冲突，从而感知统一度量工具和单位的必要性。可以利用生活情境问题引发学生的认知矛盾，体现统一度量衡的必要性，让学生经历数学知识“再创造”的过程，培养他们的量感。

例如，在教学“认识厘米”时，教师可以创设“给窗户配玻璃”的情境。

师：教室里有一块窗玻璃坏了，你该怎么告诉工人师傅这块玻璃的大小呢？

生1：需要告诉工人师傅这块玻璃的长边和短边各是多少。

师：那我们接下来分组量一量这块玻璃的长边和短边。

（小组合作操作后交流）

生2：我们用数学书的长量一量，将玻璃的长边量了2次、短边量了1次多一点儿。

生3：我们小组用手来量，玻璃的长边是4拃，短边是3拃。

生4：我们小组用笔袋量，将玻璃的长边量了3次、短边量了2次。

……

师：同样的玻璃，为什么大家测量的结果都不相同？究竟应该怎么告诉工人师傅玻璃的大小呢？

从学生的回答中可以发现，他们根据各自的具身体验选择了不同的测量工具。不同的测量方法和结果引发学生的矛盾冲突，通过思考、交流，有学生发现每个小组使用的测量工具不同，测量的结果自然也不同，要想有相同的测量结果，就要统一测量工具。还有学生发现，不仅要统一测量工具，还要统一长度单位，否则还会“乱套”。此时，教师适时播放“统一度量衡的过程”的视频。在视频中，学生感受到了从古到今统一度量衡的必要性，了解了度量衡发展的历程。这种经验的获得既有利于学生后续学习面积、体积单位，又有利于培养学生的量感。

二、在强化感知中建立标准单位的准确性

具身认知理论又称涉身认知理论或寓身认知理论。不同于“身心二元论”，具身认知理论认为人认识世界的过程就是感官通过多元方式与外界交互的过程。学生在具身体验的过程中，与外界的交互既可以对学生的感官进行刺激，让学生收获切身的知觉和体验，还可以让学生的思维过程可视化。在交互中，学生拥有沉浸式感受和切身的体验。教师要在教学中吸引学生的注意力，帮助他们建构数学知识的体系和数学思维的框架。因此，在具身学习理论的支撑下，笔者发现量感的培养是内外交互的结果，既依靠内在的脑部思维进行建构，又依靠具身的感官与外界环境进行交互。在教学中，教师要设置恰当的实践活动，让学生经历具身感知和具身体验，以强化感知的交互作用，帮助他们建立起标准单位的清晰表象。

例如，在教学“认识分米”时，教师可以设计六个交互活动，帮学生建立“1分米”的正确表象。

活动1：在直尺上找1厘米、2厘米……10厘米的长度。通过在直尺上的确认与比画，学生对1分米（10厘米）的长度有了初步认知。

活动2：在学具盒中找出长度是1分米的小棒。学生借助触觉、视觉再次感知1分米的长度。

活动3：用两根手指比画1分米的长度。小组成员互相帮助、调整，让身体的表征更准确。

活动4：抛开实物和比画出的1分米，在大脑中想象出1分米的长度，让1分米的表象更深刻。

活动5：寻找生活中的1分米。

活动6：估计身边物体的长度比1分米长还是比1分米短，再用1分米长的小棒去度量，了解“测量就是标准单位的叠加”。

在上述活动中，教师遵循学生的思维特点，调动学生视觉、触觉等多种感官，组织学生进行看、摸、比、想、找、量等活动。学生在活动中经历具身与外界的交互，思维经历从“动作”到“表象”的过程，最终准确地建立起“1分米”这个单位长度的表象。认识其他诸如厘米、毫米、平方厘米、立方厘米、千克等单位都可以运用这种多维体验的方式，让学生建立准确的表象。对于千米、吨、公顷、平方千米等离学生的生活稍远的度量单位，学生无法直接体验，教师可以选择恰当的参照物（媒介）进行对比和叠加，让学生进行间接的体验，用想象、推理等方式表征这些较大的度量单位，从而发展学生的量感。

三、在问题情境中增强具身理解的生成性

梅洛·庞蒂在“身体图式”理论中指出，具身认知具有情境性，即身体存在于环境之中，只有身体与客观环境进行交互才能获得深刻的体验。身体与环境相互依存，身体在环境中存在，环境赋予身体生存的“养料”；环境因为身体的存在焕发无限的生机。人的认知系统是个体、心智和环境“三合一”的统一体，学习过程就是在问题情境中使个体、心智和环境三者进行互动，在互动中产生新的认知。因此，教师在数学课堂中要激活学生的思维，创设恰当的问题情境，可以是教师预设好的问题，也可以是课堂中自然生成的问题。用问题引领学习，可以激发学生深层次的学习需求，唤醒他们的主体意识，加深他们对度量单位的理性认知。

例如，“认识毫米”的教学是以“厘米的认识”为基础的，教师创设“给油画配框架”的情境，设计用直尺量油画的长和宽的活动。学生通过操作，发现了油画的长比13厘米多一点，比14厘米少一点，要想准确描述油画的长和宽，就必须用新的长度单位，而且这种新的单位肯定比厘米小。于是，教师让学生分组探索比厘米小的长度单位。有的小组通过课前自学，已经知道可以将直尺上的1厘米平均分成10份，每一份就是1毫米，教师带领全班同学再次感受1毫米是1厘米细分的结果。因为有了需要才有了单位的扩充，这样，就可以准确表示油画的长是13厘米8毫米。接着，教师出示资料，有细小的仪器数据，有巨大的汽车数据，数据都是用毫米作单位。在“小”与“大”的对比中，学生提出问题“为什么汽车的数据也要用毫米作单位”。这个问题的提出，既是现实的需要，又是度量单位本质的运用。在解决问题的过程中，学生的思维不断碰撞，认知也不断丰富：毫米是因精确测量的需要而产生的。教师还可以创设情境：量讲台的长。学生只学过厘米和毫米，只用这两个度量单位去量讲台的长比较麻烦，怎么办？将已学过的长度单位进行细分已经不适用了，那么如果将已学过的长度单位进行叠加可以得到什么样的长度单位呢？将1厘米叠加，叠加10次，自然引出1分米的定义，从而揭示了分米的本质。这个问题情境将毫米、厘米、分米串在一起，让学生再次感知“度量不同的物体，需要选择合适的度量单位”“度量单位的扩充是因为需要而人为规定的”。这种感知有利于学生比较毫米、厘米、分米，从而建立三个单位之间的关联。

四、在具身反思中提升量感积累的层次性

量感的积累有三个层次：感性的量感、理性的量感和辨析的量感。感性的量感依赖直观或直觉。例如，通过观察可以获得关于物体大小的初步认知，通过比较可以获得关于数量多少的初步认知。理性的量感依赖思考或分析，例如，深入理解物体的数量和大小等物理属性。辨析的量感依赖猜想与验证，例如，解读或运用测量的结果。具身理论认为，有现实意义的学习有利于学生调动知识、技能、经验和思维。因此，在教学时，教师应引导学生进行具身反思，积累活动经验，提升量感积累的层次性。

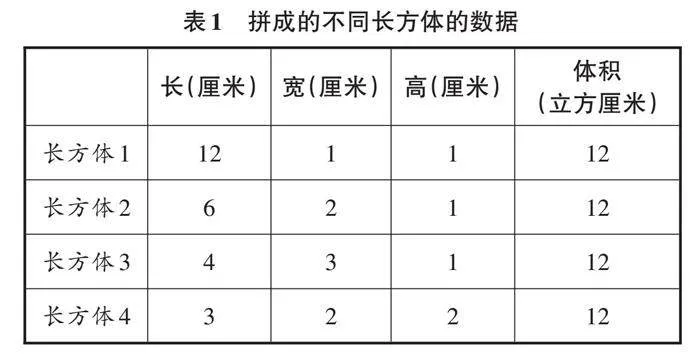
例如，在“体积和容积单位”的教学中，学生建立“1立方厘米”的表象后，教师创设了用12个1立方厘米的小正方体拼长方体的活动。学生合作拼搭并记录4种不同的长方体的数据（见表1）。

学生发现4种长方体的形状各不相同，体积却都相同。在对比中，学生通过反思，明确了测量的本质在于衡量对象所包含的度量单位数量，只需要用度量单位描述出图形的大小。在学习立方厘米、立方分米、立方米三个体积单位之后，教师引导学生讨论“这些体积单位分别适合度量生活中什么样的物体”“估算它含有多少个体积单位”。在讨论中，学生渐渐明白测量不同物体的体积需要合适的体积单位。在估算中，学生适时验证，让估计值不断接近实际值，从而提高估测和推理能力，逐步积累层次分明的量感。

五、在具身表达中感受量感积累的结构性

具身认知强调在学习中不仅要调动思维，还要调动语言、情感、想象力等。学生通过具身参与将不同度量概念进行映射，揭示度量概念间的关联，逐渐积累量感，感受量感的结构性。

教师既要将度量单位进行横向关联，又要纵向关联。横向关联是指同类的度量单位间的关联，例如，小学阶段长度单位的整体回顾有利于发现米和千米的进率的不连续性。纵向关联是指“异质”度量单位间的关联，例如，将长度单位与面积单位、体积单位进行纵向的类比、沟通，由此将探究方法迁移到其他度量单位的探究之中。

量感的形成基于度量，所有度量都是用“数量+单位”的方式表达事物的物理属性。教师要在矛盾冲突中让学生感知统一度量的必要性、在强化感知中让学生建立标准单位的准确性、在问题情境中增强学生具身理解的生成性、在具身反思中提升学生量感积累的层次性、在具身表达中构建量感积累的结构性，从而培养学生的量感。

［ 参 考 文 献 ］

[1] 赵雪梅，钟绍春.具身认知视域下促进高阶思维发展的多模态交互机制研究[J].电化教育研究，2021（8）：65-71，87.

[2] 姚丹.具身学习：为抽象的“量感”培育注入灵动的身体体验[J].考试周刊，2023（47）：68-71.

（责编 黄 露）