聚内与联外：单元整体教学实施的基本路径

［摘 要］单元整体教学中的“聚内”是指聚焦学习单元内部的本质，实现单元内的整体关联整合。单元整体教学中的“联外”是指以长程视野沟通单元间内在联系，实现跨单元、跨领域、跨学段、跨学科的融通整合。为了有效地实施单元整体教学，教师需要引导学生从“聚内”和“联外”的视角出发，理解单元内容的核心本质及其与外界的联系，从而构建完整的单元知识结构。

［关键词］单元整体教学；聚内；联外；整体建构

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）17-0088-03

教学理论与实践研究显示，单元整体教学是将零散的知识整合为系统知识，并将重复的低层次学习转变为高层次进阶学习的有效方法，这对于培养和发展学生的核心素养至关重要。然而，在小学数学的单元整体教学实践中，仍存在着理论认识与教学行为不一致，甚至出现理论与实践割裂的问题。那么，如何确保单元整体教学有效实施呢？通过分析和整理有效的教学实践案例，笔者发现“聚内”与“联外”是实现单元整体教学落地的关键路径。因此，教师需要深入理解“聚内”和“联外”的内涵，运用这两种策略去设计和实施课堂教学，从而确保单元整体教学得以实现。

一、聚内——单元内本质核心关联整合

单元整体教学旨在基于单元内容之间的内在联系，促使学生全面理解单元内容，从而培养学生的核心素养。建立在对学习内容本质理解的基础上的单元结构才有意义。学生对单元内容的学习和应用是通过多种途径进行的，所以单元整体内容应当能发散思维、关联思维，并促进知识在不同渠道的迁移。通过对单元内容本质的深刻理解，引导学生彻底把握单元内容的精髓，并在此基础上构建完整的知识结构，这是单元整体教学的真正意义。

单元整体教学中的“聚内”是指聚焦学习单元内部的本质核心，实现单元内的整体关联与整合，即聚焦一个单元内部的本质与核心而实施单元整体教学。单元本质核心是指在单元内部体现的知识概念、原理、方法、规律等，具有很强的凝聚力。在单元教学过程中若能紧扣单元核心实施单元整体教学，则能有效促进学生建构单元知识体系。

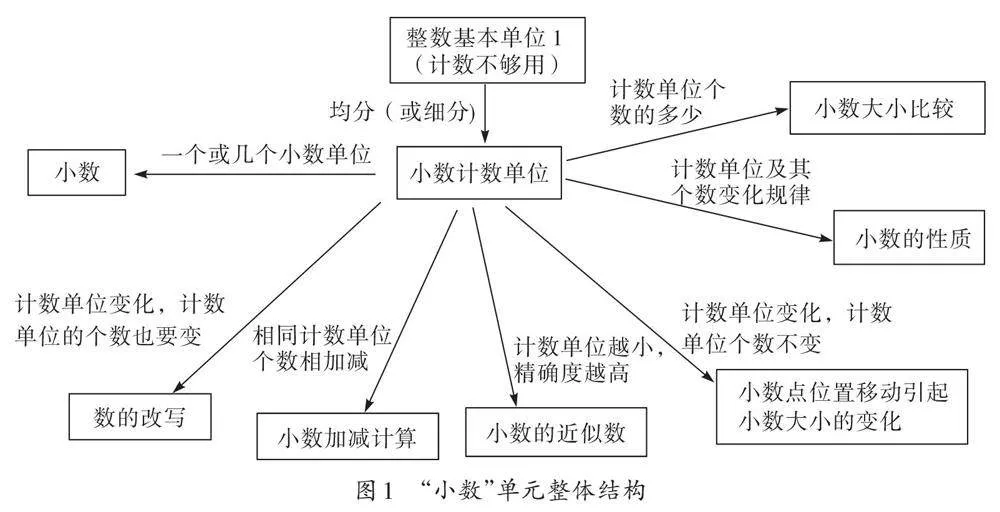
例如，在“小数”和“小数加法和减法”这两个单元中，单元内各内容的本质可以这样理解：

1.小数的意义和小数的组成实质上是十进位制和位值的体现，小数是计数单位累加的结果；

2.比较小数的大小实质上是比较相同计数单位的个数，或是比较计数单位的大小；

3.小数的基本性质是计数单位与计数单位个数的变化规律；

4.小数点移动引起小数大小变化本质是计数单位在变化；

5.小数与单位换算、数的改写体现的是计数单位变化的原理；

6.小数的近似数反映的是一个数的精确度和误差都和计数单位有关，计数单位越小，精确度越高；

7.小数的加法和减法的算理是相同计数单位的个数相加减，相加时计数单位个数满十要聚合成更大的计数单位，不够减时要将大的计数单位转化为小的计数单位再减。

通过对“小数”和“小数加法和减法”两个单元的教学内容进行本质上的解读，可以发现这两个单元的核心都围绕着“计数单位”这一概念。因此，“计数单位”成为这两个单元的核心。如果学生能够清晰地理解这两个单元的本质，那么实现单元整体结构化将变得相对容易。基于对单元内部的本质核心关联，可以引导学生在单元学习过程中建构单元整体结构（如图1）。

在小学数学课程的其他自然单元中54a16eaf640449fe755c60e67a53f17dab20001dc482f865a15bcda2648f85db，尽管可能没有一个明显的核心概念，但单元内的定义、规律和规则通常是紧密相连的。在单元整体分析的过程中，关键在于把握单元内不同概念、规律和规则的本质，并理解它们之间的根本联系和区别。通过这种方式，教师可以引导学生深入理解单元内教学内容之间的内在关联，并在此基础上构建单元知识结构。

例如，在“平行四边形和梯形”单元中，教材一共编排了7道例题：例1涉及平行与垂直的概念；例2涉及过一点画直线的垂线；例3涉及点到直线的距离；例4涉及画长方形和正方形；例5涉及平行四边形的概念；例6涉及平行四边形的不稳定性；例7涉及梯形的概念（包括等腰梯形和直角梯形）。

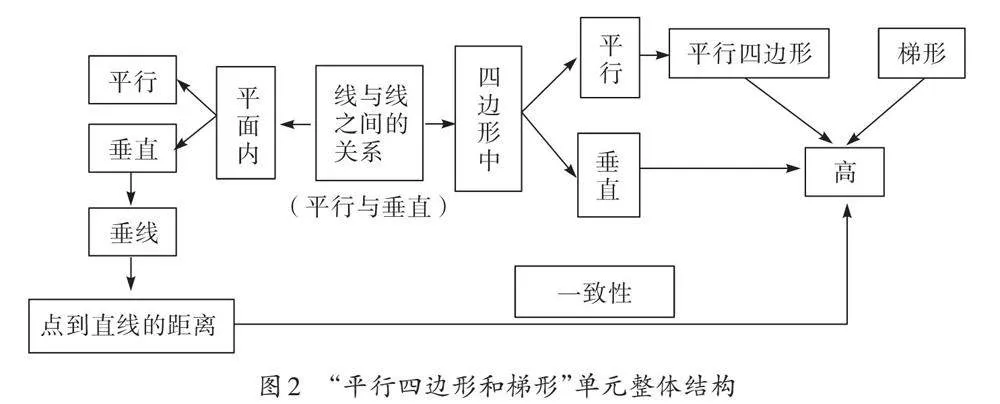
这些内容中，平行和垂直指的是同一平面内两条直线之间的位置关系，而平行四边形和梯形的定义则基于四边形中对边平行这一属性。由此可以看出整个单元内容的本质是研究线与线、边与边之间的位置关系。此外，在“平行四边形和梯形”单元中，过一点画直线的垂线、点到直线的距离、高的概念及其画法等内容，虽然表面上看似不同，但它们本质上一致。基于这样的分析，可以建构如下单元整体结构（如图2）。

基于单元内容的整体结构，可以采取整合和拓展的方式来提升教学效率。例如，将平行四边形和梯形的概念与特征放在一起教学，这有助于学生比较和发现这两类四边形的相似之处和差异。同时，平行四边形和梯形的“高”的概念以及绘制高的方法可以与点到直线的距离的教学内容并行讲解，因为它们都涉及垂直的概念。四边形之间的关系，如长方形、正方形、平行四边形、梯形等，可以通过平移、旋转等图形变换的方式进行拓展。从两组对边分别平行到相交的动态变化中，学生能够清楚地看到这些四边形之间的内在联系。这样的教学方法不仅使单元内容之间的联系更加明显和紧密，而且有助于学生深入理解整体结构。

在聚焦单元内部关系时，可以将单元内的核心概念、原理、本质内涵、数学思想方法和核心素养等作为整合的纽带和线索，同时可以用单元大观念、大概念、大问题、大任务来引领整个单元的建构。这样的教学策略能够激发学生的兴趣和参与度，进一步提高数学学习的深度。

二、联外——单元间长程视野融通整合

单元间长程视野的融通整合，简单地说就是联系单元外部的融通整合。这种整合要求师具备长远的视野，并跨越不同单元将内容进行融合和整理。在整体教学中，“单元”的概念是多层次的，它既包含教材中的自然单元，也包括根据教学目标和内容设计的整合单元，更扩展到超越这些单元的大单元。大单元的设计考虑到学生的心理发展阶段、教学内容的复杂性以及难度等级，将结构相似、方法相通的内容跨越低、中、高不同的学段进行编排。通过这样的跨单元编排和教学，教师以长远的视野、整体的关联性以及方法的融通性为指导，引导学生将统一的探究方法和本质原理迁移到不同的学段和学习过程中。这种方法不仅有助于学生建构大单元的整体知识结构，而且能够实现跨单元、跨领域、跨年级、跨学段，甚至是跨学科的知识内容之间的结构化学习。

教材把小学阶段“图形的认识”分散编排在一至六年级：一年级编排了常见立体图形和平面图的辨认；二年级编排了“角的初步认识”；三年级编排了“认识长方形和正方形”；四年级编排了“认识三角形、平行四边形和梯形”；五年级编排了“认识长方体和正方体”；六年级编排了“认识圆、圆柱和圆锥”。

尽管不同年级的图形学习内容和目标要求可能存在差异，但在认识图形特征的方法上存在共通性，即对不同图形特征的认识都是从点、线、面、角的数量、角度等方面认识的。将这种基于数量和角度的分析方法视作小学阶段图形学习的一个通用方法，有助于学生建立一个坚实的认知基础。因此，在各年级的“图形的认识”单元整体教学中，应该让学生在第一次认识图形特征时就学会这个方法，便于迁移到学习其他图形特征中。通过长程视野方法融通的方式，教材原本编排的“图形的认识”内容、单元及教学时间都不需要改变，便可以把整个小学阶段的图形知识联系起来，学生在螺旋上升的学习过程中依然能建构大单元整体结构。

例如，在教学“分数的意义”时，可以设计一个“用分数表示五线谱的全音符、二分音符、四分音符、八分音符、十六分音符的时长”的问题，引导学生融合数学知识与音乐知识解决问题，帮助学生理解跨学科知识，促进学生建构跨学科知识结构。

长程视野融通，建构跨单元一致性结构，实质上就是践行《义务教育数学课程标准（2022年版）》中关于课程内容一致性的要求。在小学阶段，许多内容虽然分布在不同学期、年级、学段、领域和学科中，但它们在结构和方法上存在相似性。对于这些内容，教师可以采用长程视野融通的策略，引导学生在学习过程中理解和掌握基本方法和共通原理，并以通理、通法建构跨学期、跨领域、跨年级、跨学段、跨学科的大单元整体结构。

总之，要使单元整体教学在课堂教学中能够有效实施，教师要站位更高、视野更宽、理解更深，这样才能在单元整体教学中引导学生从单元“内”与“外”的视角，从“聚内”与“联外”两种路径，通过理解单元内容的本质与单元内容的内外关联来建构单元整体结构，为他们的终身学习打下坚实的基础。

［ 参 考 文 献 ］

[1] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[2] 张丹，于国文.“观念统领”的单元教学：促进学生的理解与迁移[J].课程·教材·教法，2020（5）：112-118.

[3] 李帮魁，刘兴雯.把握整体意义关联 促进思维结构发展：基于单元整体教学的核心问题设计[J].小学数学教育，2021（17）：16-17.

（责编 黄 露）