三维四点六联动：单元视域下的小学数学作业设计与实施

［摘 要］针对小学数学作业现状，提出单元视域下的小学数学作业设计策略：以知识目标、应用主题为线索，以联动式单元作业设计为研究基点，通过三个维度构建“联动目标”的生态体系、四处支点探寻“联动结构”的运行方式、六条联动方式提炼“联动练习”，力求打破“作业效应”，巩固知识点、激活联动点、串联知识线、形成知识网，最终指向提升作业质量，支持和促进学生有效学习的发生。

［关键词］作业设计；单元视域；小学数学

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）17-0027-04

一、作业目标追寻

针对小学数学作业当前存在的问题，作业设计应从知识本位走向学生本位，从学习过程的整体和学生主动参与的视角构建作业设计，把作业设计当作课堂教学的必要延伸和拓展，努力做到三个“统一”：作业设计的目标与教学目标、学习目标相统一；作业的内容设计与形式设计相统一；作业设计的目标与效果相统一。单元视域下的作业观强调科学的目标体系，不仅关注作业目标、内容、实施的系统设计，还强调教与学的一致与互补，这有利于解决现有作业设计与实施存在的问题，也符合作业的系统性、整体性和发展性要求。

基于小学数学作业现状及单元视域下的作业观，笔者提出单元视域下的作业设计以作业目标、应用主题为线索，从三个维度构建作业目标体系、四个支点联动知识板块、六条策略融汇教与学的全过程，促进学生有目标有关联地学，支持和促进学生的有效学习。

二、单元视域下的作业设计

研究作业设计，首要任务是研究数学认知结构的操作方式，可通过以下4个方面为单元作业设计做好知识储备。

（一）梳理知识点

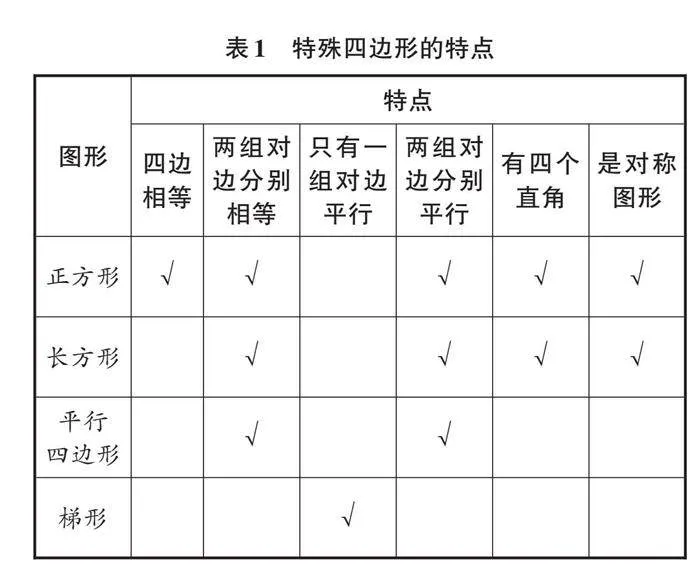
例如，在“平行四边形和梯形”的单元整理与复习中，笔者出示一张一般的四边形纸，让学生联想学过的各种四边形。学生很快就给出答案：正方形、长方形、平行四边形、梯形。笔者顺势带领学生复习这四种特殊四边形的特点，并提问：“这四种图形各有各的特点，能不能综合整理一下呢？”学生很快整理出了一个表格（见表1）。

【梳理要领】 长方形是这些图形中最基础的平面图形，一是长方形的面积计算公式是这些平面图形面积计算公式的源头；二是通过一定的变换，这些图形都可以转化成长方形。教师有序梳理不同图形的特点以及它们之间的联系，为学生的数学认知体系构建框架。

（二）发掘联动点

与某一知识点相关联的内容点都可以称为联动点。联动点与该知识点紧密相关，主要反映该知识点的属性、特征以及学习者的经历、情感等。以“平行四边形”为例，发掘联动点的方法见表2。

平行四边形的联动点有很多。这几类联动点分别指向知识、技能、思想、经验、情感等不同的方面，看似独立又相互联系，体现了解决问题的基本能力。

【发掘要领】通过学生已有的经验切入，对该知识点进行加工、改造形成联动点。也可以借助操作切入，从学生的活动中展开，调动多种感官参与学习形成联动点等。

（三）串成知识线

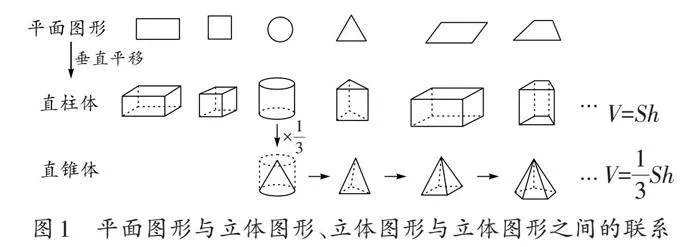
将孤立、碎片化的知识点关联起来，引导学生在新旧知识、经验间建立联系，帮助学生建构或重构清晰的知识脉络。以“立体图形的体积（总复习）”为例（如图1），分析图形之间的联系。

笔者先引导学生经历动态梳理、沟通的过程，揭示点、线、面、体之间的内在联系，将原本孤立、碎片化的学习内容通过梳理整合而建立联系。接着，笔者带领学生沟通、梳理“平面图形—直柱体—直锥体”的内在关系，建构起从“要素沟通”到“系统构建”完整的体积知识体系。

【联动要领】联动作业设计有利于知识从“孤立碎片”走向“联系整合”。通过练习，找寻新旧知识间的内在联系并提升认知水平，为新知学习、构建联动提供强有力的附着点。

（四）形成知识网

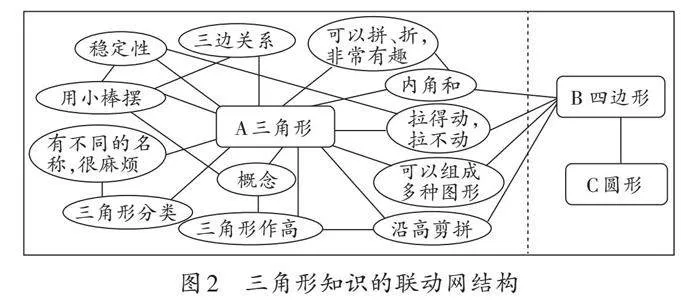
数学认知结构最基本的形式有三种：线性结构、树形结构和联动网结构。以联动网结构为例，分析“三角形”的知识点（如图2）。

【构建要领】图中的A，B，C三个圆角矩形代表三类知识点，12个椭圆形代表联动点，连接知识点与联动点、联动点与联动点之间的是知识线。通过联动点及知识线，将三角形的数学认知结构链接到平行四边形的数学认知结构中，从而形成更大的知识体系。联动网状认知结构的形成需要多种教学因素的参与。教师要善于挖掘联动点、设计有效知识线，组织起有利于知识探索、能力锻炼的练习流程，促进认知结构的形成。

三、单元视域下的作业实施

数学不是一门孤立的学科 ，要让学生会学数学、善于应用数学，可以基于以下方面实施单元作业策略。

（一）基于基本内容的单元作业整合

第一步：基础练习

[练习]请在方格纸上画出面积是12cm2的平行四边形。

[说明]已知面积作图，意在让学生先测算出平行四边形的底和高。逆向运用平行四边形的面积计算公式，培养学生的估算能力和图形感知力。

第二步：联动板块

[板块]请在方格纸上画出面积是12cm2的所有三角形和梯形。

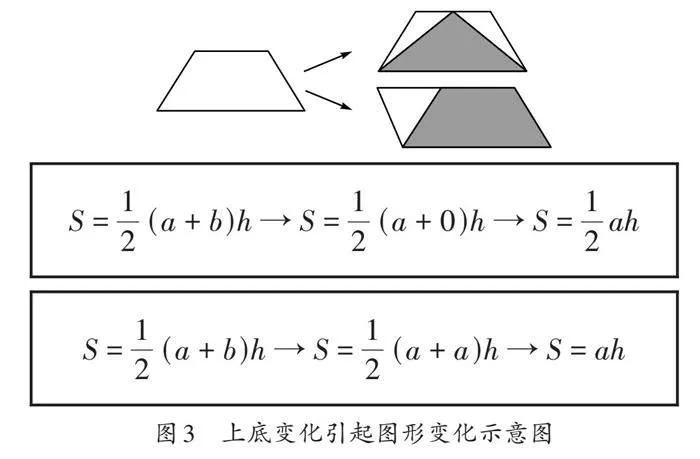
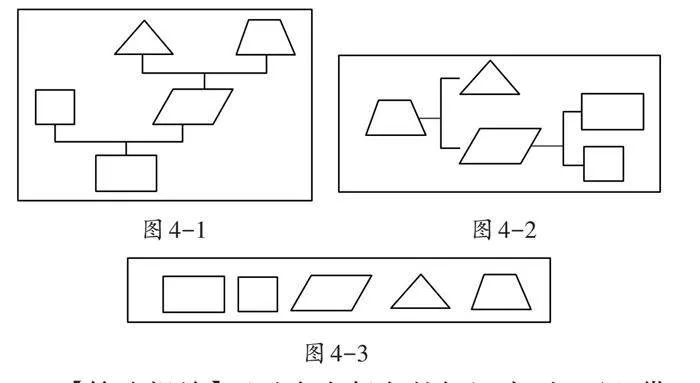
第三步：分析图形结构与内在关系（如图3）

通过示意图，学生发现所学图形可以通过梯形转化得到（如图4-1），还梳理出不一样的层次图（如图4-2、图4-3）。

【策略提炼】面对多个复杂的知识点时，可以借助关系示意图沟通知识点之间的联系。依托各种关系开发出千变万化的联动习题，并通过解答、辨析，构建新的知识联动网。

（二）基于核心知识的单元作业深化

围绕核心知识将相关的知识点联系起来，使学生头脑中形成一条清晰的知识链，从空间上帮助学生形成知识结构。以“图形的切割”为例，过程如下。

1.串联核心知识之“序”

第一步：基础练习

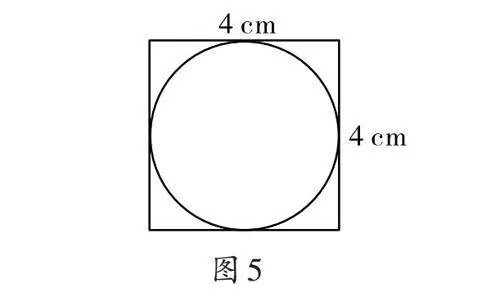
[练习]在一个正方形（如图5）中挖一个最大的圆，面积是多少？

[说明]思考最大的圆与正方形面积之间的关系。

第二步：联动板块

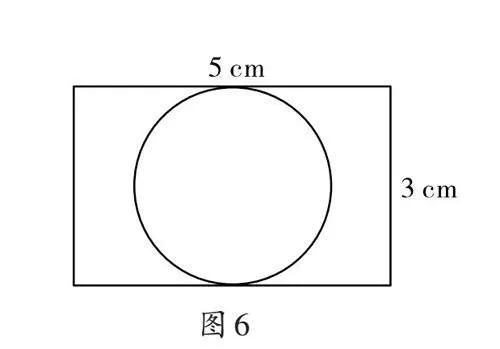
[板块①]图6中最大圆的面积是多少？思考：长方形中挖一个最大的圆要注意什么？如果是半圆呢？

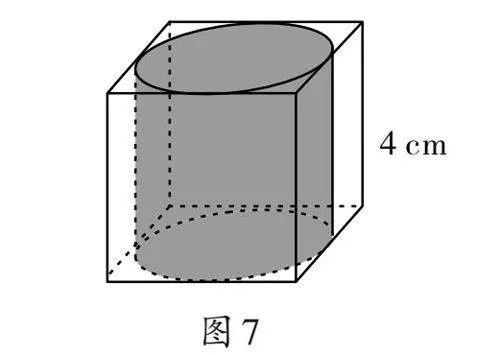
[板块②]如图7，在一个棱长为4 cm的正方体中削出一个最大的圆柱，体积是多少？思考：圆柱与正方体的体积之间有什么关系？

第三步：辨析

[想一想]这几道题之间有什么联系？你是怎么理解的？要使圆柱的体积最大，要关注哪些方面？是不是以最大面做底面？

【策略提炼】从探究正方形中最大的圆入手，到长方形中最大的圆，再到立体图形中最大的圆柱，按知识的发展之“序”串联，逐层推进，旨在培养学生的空间观念，让学生掌握分析问题的方法，使不同水平层次的学生都能在学习的过程中得到发展。

（三）基于思想方法的单元作业拓展

以数学思想方法为核心，开展作业拓展设计，整体体现数学思想方法，用数学思想方法统领整个单元。以“长方体的体积”为例，开发练习中蕴含的思想方法。

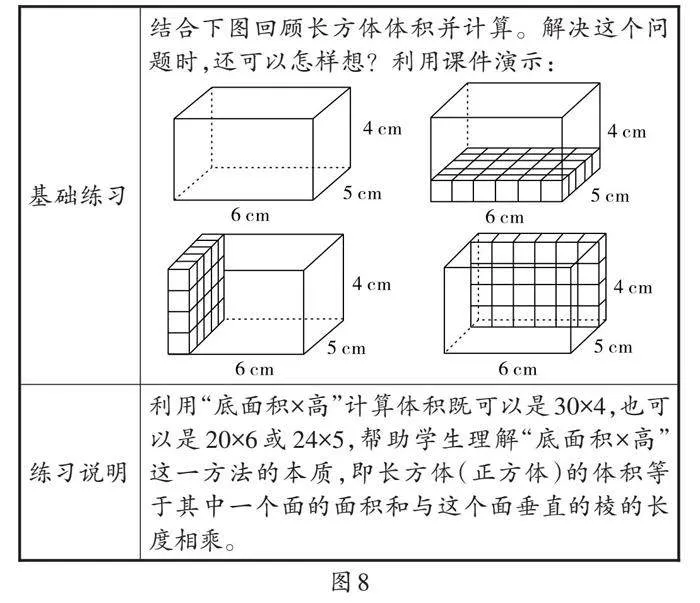
第一步：基础练习（如图8）

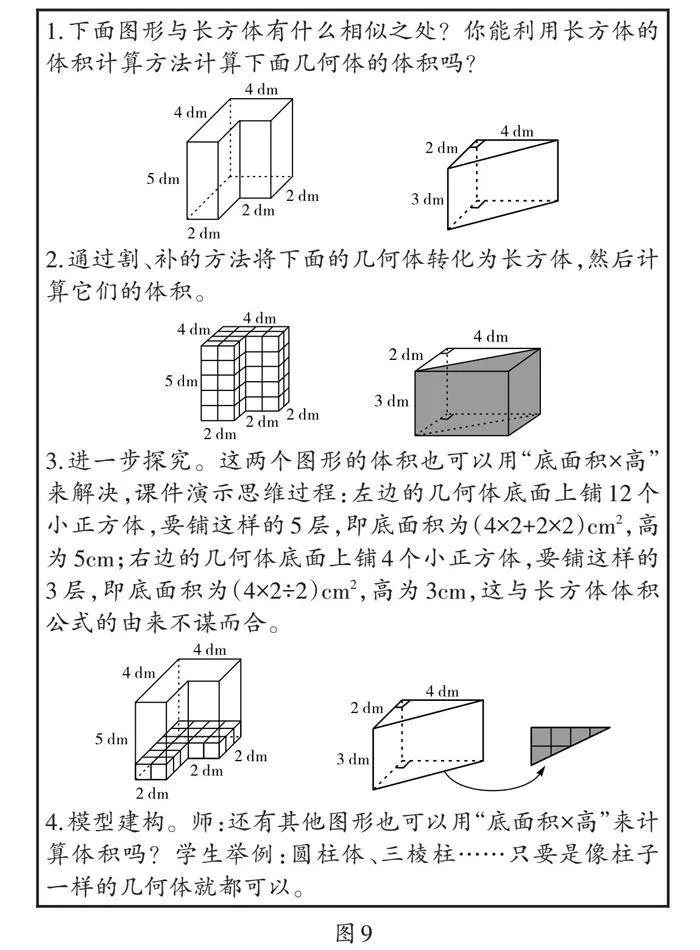
第二步：联动板块（如图9）

第三步：辨别、分析

从基础的图示化问题到增加变式的图示化问题，最后建构模型——“柱体体积=底面积×高”。在这个过程中，学生的思维不断走向深处。

【策略提炼】学生将所学的数学知识应用于问题解决时，会发现许多现实问题和数学模型并不“和谐”，因此需要突破定式、理解本质。学生对“底面积×高”的理解通常拘泥于“下底面的面积×高”，而从基础的图示化问题到增加变式的图示化问题，可助力学生建构柱体体积的计算模型——“柱体的体积=底面积×高”。

四、总结思考

研究单元视域下的小学数学作业设计与实施后，笔者对教材、对学生、对单元作业设计、对学生的学习过程都有了更深刻的认识。研究成果如下：

第一，构建了“联动目标”的生态体系。通过研读知识的学科目标、开发练习的价值目标、挖掘学生的能力目标，多渠道构建“联动目标”的生态体系，有效激发了学生的探究欲望。

第二，确定了“联动结构”的运行方式。通过梳理基本点，充分拓展“联动结构”的宽度；通过挖掘联动点，真正加深“联动结构”的深度；通过连接知识线，不断拉伸“联动结构”广度；多维度生成“联动结构”，有效激活了学生的数学思维。

第三，优化了“联动练习”的实施策略。通过单元基本内容的整合设计，达到“固点联线串面”之效；围绕单元核心知识深化设计，将知识从时间上串联起来，从空间上并联起来，力求连接知识的“序”，整合知识的“块”，帮助学生构建以核心知识为主的知识网络；挖掘和开发单元作业所蕴含的数学思想方法，将隐性思想方法以显性的作业形式呈现，渗透思想、强化体验。

单元视域下的作业设计与实施，只是作业研究领域的一个方面。从作业管理视角出发，作业设计又与作业布置、作业过程指导、作业批改与反馈相关联。作业不只有线下的，还有线上的，如何与信息化相结合也是未来作业设计需要探索的。从这些角度看，作业设计与实施研究还存在广阔空间。

［ 参 考 文 献 ］

[1] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[2] 汪月芬.重构作业：课程视域下的单元作业[M].北京：教育科学出版社，2021.

[3] 杜威.我们如何思维[M].马明辉，译.上海：华东师范大学出版社.2020.

[4] 吴春枝.小学数学练习设计的有效性实践研究[J].当代教研论丛，2020（4）：13.

（责编 吴美玲）