考虑材料硬度与缩径量的橡胶衬套各向刚度优化设计

秦武 李春归 潘兵兵 李骏 刘霏霏

收稿日期：2023?10?19

基金项目：国家自然科学基金（51806066）；博士后科学基金项目（2022M711352）；江西省自然科学基金资助项目（20232BAB214047）；江西省教育厅科技项目（GJJ210630）

文章编号：1005-0523（2024）03-0090-11

摘要：【目的】通过对橡胶衬套各向刚度的优化设计以指导产品设计，以期大幅缩短橡胶衬套的研发周期。橡胶衬套作为新能源汽车、特种车辆、动车组等载运工具的重要连接件，对整车操纵稳定性起着至关重要的作用。【方法】为了避免工程实践中反复调试的繁琐工作，提出了一种考虑材料硬度与缩径量的橡胶衬套各向刚度（径向刚度、轴向刚度、偏摆刚度和扭转刚度）优化设计方法。首先，采用Ogden模型作为橡胶衬套的本构模型，通过试验设计与有限元分析相结合的方法，计算不同内芯外径、橡胶高度、缩径量和材料硬度下衬套各向刚度；然后，建立各向刚度的二阶响应面模型，利用拉丁超立方抽样和方差分析，检验响应面模型精度；最后，根据遗传算法，建立含各向刚度为设计变量的多目标优化模型，并对优化结果进行试验验证。【结果】研究表明：径向刚度、轴向刚度、偏摆刚度和扭转刚度的试验结果与目标值的相对误差分别为7.72%，9.06%，-6.33%和9.16%，均在±10%以内，满足工程应用的要求。【结论】试验结果验证了所建立的各向刚度二阶响应面模型的有效性，以及所提出优化设计方法的可行性，为橡胶衬套产品设计提供指导，可极大地缩短橡胶衬套的研发周期。

关键词：橡胶衬套；响应面方法；遗传算法；多目标优化

中图分类号：U467.3 文献标志码：A

本文引用格式：秦武，李春归，潘兵兵，等. 考虑材料硬度与缩径量的橡胶衬套各向刚度优化设计[J]. 华东交通大学学报，2024，41（3）：90-100.

Optimal Design of Isotropic Stiffness for Rubber Bushing by Considering Material Hardness and Diameter

Reduction for Conveyance

Qin Wu1，2， Li Chungui1， Pan Bingbing2， Li Jun1， Liu Feifei1

（1. School of Mechatronics & Vehicle Engineering， East China Jiaotong University， Nanchang 330013， China；

2. Jianxin Zhao's Technology Co. Ltd.， Ningbo 315615， China）

Abstract： 【Objective】As an important connecting part of new energy vehicles， special vehicles， locomotives and other means of transportation， rubber bushing plays a crucial role in the stability of the whole vehicle handling. In order to avoid the tedious work of repeated debugging in engineering practice， 【Method】an optimal design method of rubber bushing all-directional stiffness （radial， axial， yaw and torsional stiffness） taking into account the material hardness and diameter reduction is proposed. Firstly， the Ogden model is used as the constitutive model of rubber bushing. Second， by combining experimental design with finite element analysis， the isotropic stiffness of rubber bushing with different inner core outer diameter， rubber height， diameter reduction and material hardness is calculated. The second-order response surface model of isotropic stiffness is established and the accuracy of the model is verified by Latin hypercube sampling and variance analysis. Finally， a multi-objective optimization method of isotropic stiffness of rubber bushing is proposed using genetic algorithm to testify the optimization result. 【Result】 The result shows that the relative errors between the measured radial， axial， yaw and torsional stiffness and objective stiffness are 7.72%， 9.06%， -6.33% and 9.16% respectively， which are all within ±10% and meet the requirements of engineering application. 【Conclusion】 The validity of the established second-order response surface model of isotropic stiffness and the feasibility of the proposed optimization design method are verified to provide guidance for the product design of rubber bushing， which can greatly shorten the research and development cycle of rubber bushing.

Key words： rubber bushing; response surface method; genetic algorithm; multi-objective optimization.

Citation format： QIN W， LI C G， PAN B B， et al. Optimal design of isotropic stiffness for rubber bushing by considering material hardness and diameter reduction for conveyance[J]. Journal of East China Jiaotong University， 2024， 41（3）： 90-100.

【研究意义】橡胶衬套作为一种重要的连接元件，主要安装在悬架、副车架、转向架、稳定杆等位置，被广泛应用于新能源汽车、特种车辆、动车组等载运工具和轨道交通领域中[1]。橡胶衬套材料硬度与结构决定着衬套的刚度。若刚度设计过大，对载运工具振动与噪声控制不利；若刚度设计过小，载运工具或其子系统行程太大，会影响整车操纵稳定性。因此，优化设计衬套刚度对整车性能的提升起着至关重要作用。

【研究进展】在橡胶衬套刚度影响因素研究中，缩径量影响着衬套的各向刚度，在工程上，缩径量可定义为：橡胶衬套外套直径的压缩变化量。方红和陈宝等[2-3]研究表明，可以合理控制缩径量尺寸来调整橡胶衬套刚度，当缩径值达到一定程度后对橡胶衬套静、动刚度值的影响变大。曾家兴和陈宝等[4-5]研究发现，不同材料硬度对橡胶弹簧超弹本构模型参数和弹簧垂向刚度有显著影响，且硬度越大，静刚度变化越明显。

在橡胶衬套刚度优化算法研究中，目前有基于各种优化理论的算法。较为成熟的有差分进化算法[6]、自适应模拟退火算法[7]、新型混沌磷虾群优化算法[8]和遗传算法[9]等，被广泛应用于橡胶衬套刚度优化中。目前，国内外对于橡胶衬套刚度优化开展了研究工作。

Dai等[10]采用混合神经网络模型开发了橡胶衬套的详细模型，并识别其关键参数。Jung等[11]基于衬套形状设计变量与有限元分析预测的刚度值之间的关系，在人工神经网络模型中训练了多层感知器和卷积神经网络模型，准确预测橡胶衬套刚度。柯俊等[12]通过有限元法计算推力杆球铰橡胶衬套的应变分布特征和刚度参数，建立推力杆球铰的多目标优化模型，采用遗传算法得到最优球铰结构参数的优化方案。郭一鸣等[13]对悬置中非橡胶填充结构进行优化设计，通过谢菲尔德遗传算法对结构参数进行优化，以满足动力总成悬置系统匹配过程中悬置的刚度要求。

【创新特色】综上所述，已有相关研究通过优化算法，对橡胶衬套结构参数进行优化，设计橡胶衬套的刚度，改善整车操纵稳定性。但是，目前基于橡胶衬套刚度优化研究方面还存在以下问题：鲜有综合考虑衬套各向刚度优化设计方面的研究，绝大多数研究只考虑衬套径向刚度和轴向刚度，而忽略了偏摆刚度和扭转刚度，可能会导致车辆在俯仰及侧倾方向上行程过大，影响车辆操纵稳定性；绝大多数研究从衬套结构角度上只针对材料硬度或缩径量进行单一变量分析，并未考虑二者对橡胶衬套各向刚度的综合影响。

【关键问题】因此，本文以某车辆悬架中橡胶衬套为研究对象，提出了一种考虑材料硬度与缩径量的橡胶衬套各向刚度优化设计方法。采用试验设计与有限元分析相结合的方法，并通过试验验证有限元模型的准确性。建立各向刚度与参数变量的二阶响应面模型，以拉丁超立方抽样和方差分析对响应面模型进行精度检验。利用遗传算法实现多目标优化获取最优参数，并将优化结果进行试验验证。试验结果表明：各向刚度试验结果与目标刚度的相对误差分别为7.72%，9.06%，-6.33%和9.16%，均在±10%以内，满足橡胶衬套刚度匹配要求。

1 橡胶衬套有限元建模及试验验证

1.1 橡胶衬套有限元模型建立

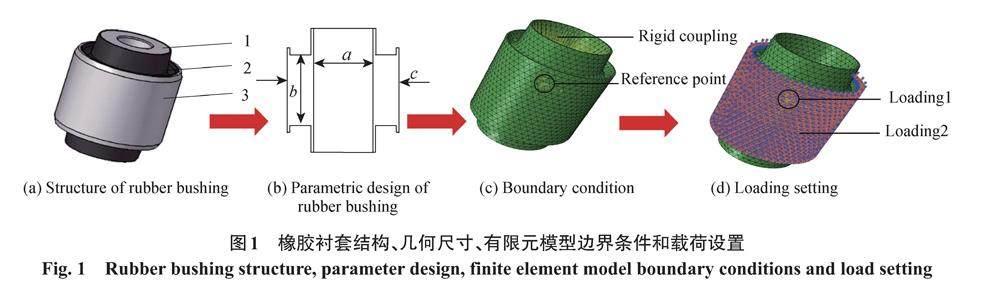
橡胶衬套有限元建模过程如图1所示。其中橡胶衬套主要由金属部分的内芯、外套和橡胶部分组成，如图1（a）所示。所研究的橡胶衬套结构在径向和轴向上采用了对称设计，两个径向刚度和两个偏摆刚度在相同载荷作用下结果相同，即所述的橡胶衬套4个方向刚度可以代表6个方向刚度。故本文采用“各向刚度”表述。

选取对橡胶衬套各向刚度影响较大的因素作为设计变量，考虑内芯外径[a]、橡胶高度[b]、缩径量[c]和材料硬度[d]作为参数变量[14]，如图1（b）所示。

橡胶衬套在承载过程中主要是橡胶部分发生变形，金属部分的变形很小，可以忽略不计。为了简化橡胶衬套模型，在刚度计算时只对橡胶部分进行有限元分析。

根据图1（a）所示的橡胶衬套结构，先利用Hypermesh软件对橡胶衬套几何模型进行网格划分，再将网格导入Abaqus软件中，建立如图1（c）和图1（d）所示的有限元模型。图1（c）为边界条件，图1（d）为载荷设置，加载点1为内表面与形心处参考点的刚性耦合点，加载面2为衬套施加载荷的外表面。

不同的材料硬度影响橡胶衬套超弹性本构模型参数，使得有限元仿真计算的刚度值相差较大。通常采用应变能密度函数来准确描述橡胶材料的应力-应变关系，采用Ogden模型作为橡胶衬套的本构模型，来描述橡胶材料的超弹性变形特性[15]。

Ogden模型的应变能密度函数形式为

[U=i=1N2μiαi2（λ1αi+λ2αi+λ3αi-3）+i=1N1DiJ-12i] （1）

式中：[U]为应变能密度；[μi]和[αi]为试验测定的材料参数；[Di]为不可压缩参数；[λi]为伸长比；N为Ogden模型的阶数，通常可以选择为3；[J]为变形体积与未变形体积之比。

与其他本构模型比较，Ogden本构模型能更好的适用于橡胶材料的非线性、大变形特性，具有较好的拟合精度。因3阶Ogden模型参数较少，计算和实现相对简单，工程上常用3阶Ogden模型用于橡胶衬套本构模型的拟合。基于单轴拉伸、双轴拉伸和平面剪切试验，拟合得到材料参数如表1所示。

根据橡胶衬套的实际工况载荷，在加载点1处，施加1 mm的位移或0.1°的转角载荷；在加载面2处，加载缩径量大小，并同时约束6个方向的自由度；最后，提取对应的力（力矩）与位移（转角）的变化曲线，仿真得到衬套各向刚度。

1.2 橡胶衬套有限元模型试验验证

采用MTS831弹性体试验台（力值：±25 kN，位移：±30 mm，频率：0～400 Hz，温度：-100～+500 ℃，精度：0.2%）测试衬套的径向刚度和轴向刚度，通过MTS零部件试验台（扭矩：±565 N·m，角度：±45°，频率：0～100 Hz，温度：-70～+170 ℃，精度：0.2%）测试衬套的偏摆刚度和扭转刚度，以验证有限元模型的准确性，试验设备如图2所示。

橡胶衬套通过夹具固定在试验台架上，激励装置缓慢对橡胶衬套施加载荷，通过传感器连续记录施加在衬套上的载荷和橡胶衬套变形量。预加载1次，取第2次加载过程的力（力矩）和位移（转角）曲线，计算出对应方向的刚度。

对橡胶衬套模型进行有限元仿真分析，并将橡胶衬套进行试验测定，仿真结果和试验结果对比如图3所示。

通过比较仿真曲线和试验曲线，并对数据进行拟合处理，初始衬套径向刚度[Kx]、轴向刚度[Kz]、偏摆刚度[Knx]和扭转刚度[Knz]的有限元仿真与试验数据对比如表2所示。

由表2可以看出，试验结果稍大于仿真结果，相比于有限元仿真结果，径向刚度、轴向刚度、偏摆刚度和扭转刚度的相对误差分别为5.12%，4.69%、

-7.27%和3.60%，均在±10%以内，在后续的各向刚度优化处理中，可采用橡胶衬套有限元模型进行分析；产生误差的主要原因是在仿真分析时简化了橡胶衬套模型，忽略了金属部件（内芯和外套）的变形。

2 橡胶衬套各向刚度响应面建模及分析

2.1 响应面模型建立

考虑响应变量和自变量的线性和非线性关系以及自变量间的交互作用，通过引入响应面方法，拟合各向刚度值与参数变量的关系。基于前期研究，相比于一阶响应面模型，二阶响应面模型拟合效果会更好，故本文采用二阶响应面模型。所建立的二阶响应面模型为

[Y=β0+i=1nβixi+i=1nβiixi2+ ij（i

式中：[Y]为响应变量；[β0]和[βi]为多项式系数；[xi]和[xj]为设计变量；[n]为设计变量的个数。

考虑缩径工艺的要求，橡胶衬套的缩径量一般应在5%以下，初始橡胶衬套的橡胶缓冲厚度为8 mm，基于上下波动原则取缩径量分别为0.2，0.3 mm和0.4 mm。不同材料硬度对橡胶衬套的本构模型和刚度影响较大，当材料硬度大于68 SHA时，隔振器的静、动刚度值随硬度的变化速率超过了50%，橡胶隔振器已失去隔振作用[16]。对于新能源汽车、特种车辆等载运工具，工程上常使用50，55 SHA和60 SHA的车用橡胶衬套。

通过试验设计研究因素对橡胶衬套径向刚度、轴向刚度、偏摆刚度和扭转刚度的影响程度，按照上下波动原则分别对4个因素均匀取3个水平，初始值及区间取值如表3所示。

由表3可知，试验设计为4因素3水平，选取试验设计中心点数为3，确定了27组试验[17]，试验设计结果如表4所示。

根据式（2），建立衬套各向刚度的二阶响应面模型为

[ki=γ1+γ2a+γ3b+γ4c+γ5d+γ6ab+       γ7ac+γ8ad+γ9bc+γ10bd+γ11cd+       γ12a2+γ13b2+γ14c2+γ15d2] （3）

式中：[ki]为各向刚度的数值（[i=x，y，nx，nz]），不含单位；[γj]为系数（[j=1，2，…，15]）。上式应为无量纲计算公式，即等式左右两边无单位。

将试验设计中的27个样本点代入式（3）中，通过最小二乘法拟合各向刚度二次多项式响应面近似函数系数，式（3）中系数见表5。

2.2 响应面模型精度分析

采用拉丁超立方抽样方法，随机选取20个样本点对响应面近似模型的拟合程度进行验证[18]。通过样本点的响应值和预测值之间的相关程度来评价响应面模型的精度，统计学中常用决定系数[R2]来表征响应面模型的逼近程度。决定系数的计算公式为

[R2=1-QCQZ] （4）

[QC=i=1n（yi-ypi）2] （5）

[QZ=i=1n（yi-y）2] （6）

[y=1ni=1nyi] （7）

式中：[QC]为残差平方和；[QZ]为偏差平方和；[n]为样本点数目；[yi]和[ypi]分别为第[i]个样本点的响应值和预测值；[y]为所有样本点的响应值的均值。当[R2]越接近于1，表示响应面拟合效果越好。表6为衬套各个方向的决定系数。

从表6可见，各向刚度的响应面模型的决定系数均大于0.9且接近于1，响应面模型拟合程度较高，可用于多目标优化。

对表4数据进行因素分析，得到各个变量对橡胶衬套各向刚度的影响程度和贡献率，分析结果见表7。表7中的[F]值为统计检定值，[F]值越大，说明变量对刚度结果影响越大

[F=R2/（k-1）（1-R2）/（n-k）] （8）

式中：[F]为各向刚度统计检定值；[n]为全部观测值个数；[k]为因素水平个数。

分析表7的数据可知：内芯外径[a]对径向刚度的影响最显著，贡献率为93.21%；内芯外径[a]和材料硬度[d]对轴向刚度的影响较大，贡献率分别为67.93%和27.49%；内芯外径[a]对偏摆刚度的影响最显著，贡献率为83.79%；内芯外径[a]和材料硬度[d]对扭转刚度的影响较大，贡献率分别为80.43%和18.30%。

为了分析材料硬度和缩径量及其交互作用对橡胶衬套各向刚度的影响，由响应面模型绘制的部分响应曲线如图4所示。

由图4分析可知，材料硬度与缩径量对橡胶衬套径向刚度、轴向刚度、偏摆刚度和扭转刚度的交互作用不明显，且在一定范围内，橡胶衬套径向刚度、轴向刚度、偏摆刚度和扭转刚度随着材料硬度和缩径量的增大而增大。

3 橡胶衬套各向刚度优化设计

3.1 目标函数设计

基于建立的响应面模型，以内芯外径a、橡胶高度b、缩径量c和材料硬度d为设计变量，以橡胶衬套的径向刚度kx、轴向刚度kz、偏摆刚度knx和扭转刚度knz为目标，进行多目标优化设计。

目标刚度kx取值为8 000 N/mm，kz取值为320 N/mm，knx取值为6 N·m/（°），knz取值为1.2 N·m/（°）。利用均值化法对目标函数进行无量纲化，建立目标函数如式（9）。目标函数值越小，各向刚度与目标刚度越接近

[minf=i=14Fiai ] （9）

[F1=kx-8 000F2=kz-320F3=knx-6F4=knz-1.2] （10）

[ai=j=1mkxj-kx0m] （11）

式中：[Fi]为各向刚度与目标刚度的差值；[kxj]为各向刚度；[kx0]为目标刚度；[m]为试验设计的数目，m=27；[ai]为无量纲化后的分配系数，即试验设计中各向刚度与目标刚度差值的绝对值求和后的平均值，具体取值见表8。

约束条件设置为：[21 mm≤a≤25 mm;25 mm≤][b≤27 mm;0.2 mm≤c≤0.4 mm;50 SHA≤d≤60 SHA。]

3.2 优化结果分析

NSGA-Ⅱ遗传算法引入拥挤度计算和精英策略，避免优化过程中产生局部收敛，具有较高的计算效率和鲁棒性，被广泛应用于多目标优化问题[19]。本文采用MATLAB软件运行NSGA-Ⅱ遗传算法，并对橡胶衬套各向刚度进行多目标优化。设置初始化种群数为50、最大迭代次数为200、交叉比例为0.8、变异概率为0.05，步长分别设置为0.01，0.01，0.01，5。遗传迭代运算后，得到目标函数值及最优参数，优化结果如表9所示。

通过对比表9中的非劣解集，第9组数据的目标函数值最小，对第9组数据中的参数取整，取整后的最优参数为内芯外径25 mm、橡胶高度26 mm、缩径量0.4 mm，材料硬度50 SHA。根据取整后的最优解参数设计橡胶衬套成品并进行刚度测试试验，对比各向刚度和目标刚度，如图5所示。

由图5可见，橡胶衬套各向刚度的试验值与目标刚度接近。通过二阶响应面模型计算出的结果、有限元仿真的分析结果以及试验结果分别与目标值进行对比，见表10。

分析表10中的数据可知，根据优化结果对橡胶衬套参数取整后分析，代入响应面模型拟合后的轴向刚度kx，kz分别为8 049.40，319.03 N/mm，扭转刚度knx，knz分别为6.29，1.34 N·m/（°），与目标值的误差分别为0.62%，-0.3%，4.83%和11.67%；有限元仿真后的轴向刚度kx，kz分别为8 184.00，333.56 N/mm，扭转刚度knx，knz分别为6.11，1.27 N·m/（°），与目标值的误差分别为2.3%，4.24%，1.83%和5.83%；试验测定后的轴向刚度kx，kz分别为8 617.96，348.98 N/mm，扭转刚度knx，knz分别为5.62，1.31 N·m/（°），与目标值的误差分别为7.72%，9.06%，-6.33%和9.16%，刚度值误差均在±10%以内，符合工程应用的要求。

4 结论

本文在橡胶衬套各向刚度优化设计中考虑了材料硬度和缩径量的影响，基于试验设计与有限元分析相结合的方法，建立橡胶衬套各向刚度的二阶响应面模型，采用NSGA-Ⅱ遗传算法对各向刚度进行多目标优化研究，得出以下结论：

1） 建立关于内芯外径、橡胶高度、缩径量和材料硬度随衬套各向刚度变化的二阶响应面模型，并验证了模型的有效性，可为载运工具橡胶衬套各向刚度优化设计提供必要条件。

2） 缩径量对橡胶衬套轴向刚度和偏摆刚度影响较大，贡献率分别为42.9%和50.5%，通过增大缩径量，可有效提高轴向刚度，提高产品的耐久性；材料硬度对衬套轴向刚度和扭转刚度影响较大，贡献率分别为45.6%和30.4%，通过增大材料硬度，可有效提高扭转刚度，提高整车操纵稳定性。

3） 采用NSGA-Ⅱ遗传算法对橡胶衬套各向刚度进行多目标优化，并将优化结果进行试验验证，各向刚度试验结果与目标值的相对误差分别为7.72%，9.06%，-6.33%和9.16%，均在±10%以内，满足工程应用的要求，可有效的避免工程实践中反复调试的繁琐工作，从而极大地缩短了产品研发周期。

参考文献：

[1]   LI L， SUN B HUA H. Analysis of radial stiffness of rubber bush used in dynamic vibration absorber[J]. Journal of Southeast University， 2019， 35（3）： 281-287.

[2]   方红， 李晨芳， 辛振祥. 缩径尺寸对橡胶衬套刚度耐久性的影响[J]. 中国机械， 2020： 183-184.

FANG H， LI C F， XIN Z X. Effects of reduction size on the stiffness and durability of rubber bushings[J]. China Machinery， 2020： 183-184.

[3]   陈宝， 代正莉， 付江华， 等. 汽车悬架衬套静动特性分析中缩径量影响研究[J]. 噪声与振动控制， 2019， 39（1）： 126-130.

CHEN B， DAI Z L， FU J H， et al. Study on the influence of shrinkage in the static-dynamic characteristic analysis of automotive suspension bushings[J]. Noise and Vibration Control， 2019， 39（1）： 126-130.

[4]   曾家兴， 丁智平， 林胜， 等. 胶料硬度对超弹本构模型参数及橡胶弹簧刚度的影响[J]. 湖南工业大学学报， 2018，32（3）： 92-96.

ZENG J X， DING Z P， LIN S， et al. Effect of rubber hardness on parameters of superelastic intrinsic model and rubber spring stiffness[J]. Journal of Hunan University of Technology， 2018， 32（3）： 92-96.

[5]   陈宝， 张鑫， 代正莉， 等. 硬度对橡胶力学特性与悬架衬套刚度的影响[J]. 噪声与振动控制， 2020， 40（6）： 222-227.

CHEN B， ZHANG X， DAI Z L， et al. Effect of hardness on mechanical properties of rubber and suspension bushing stiffness[J]. Noise and Vibration Control， 2020， 40（6）：222-227.

[6]   KAYA N， ERKEK M Y， GUVEN C. Hyperelastic modelling and shape optimisation of vehicle rubber bushings[J]. International Journal of Vehicle Design， 2016， 71（1/2/3/4）： 212-225.

[7]   DONG Y， YAO X， XU X. Cross section shape optimization design of fabric rubber seal[J]. Composite Structures， 2021， 256： 113047.

[8]   BILAL H， OZTURK F. Rubber bushing optimization by using a novel chaotic krill herd optimization algorithm.[J]. Soft Comput， 2021， 25， 14333-14355.

[9]   丁智平， 曾家兴， 林胜， 等. 橡胶弹簧结构强度分析及参数优化[J]. 振动与冲击， 2019， 38（12）： 246-251.

DING Z P， ZENG J X， LIN S， et al. Structural strength analysis and parameter optimization of rubber springs[J]. Vibration and Shock， 2019， 38（12）：246-251.

[10] DAI L， CHI M， XU C， et al. A hybrid neural network model based modelling methodology for the rubber bushing[J]. Vehicle System Dynamics， 2022， 60（9）： 2941-2962.

[11] JUNG Y W， KIM H K. Prediction of nonlinear stiffness of automotive bushings by artificial neural network models trained by data from finite element analysis[J]. Automot.Technol， 2020， 21： 1539-1551.

[12] 柯俊， 祖洪飞， 史文库. 基于有限元法及遗传算法的推力杆球铰多目标优化方法[J]. 汽车工程， 2020， 42（2）： 178-183.

KE J， ZU H F， SHI W K. Multi-objective optimization method of thrust rod ball hinge based on finite element method and genetic algorithm[J]. Automotive Engineering， 2020， 42（2）： 178-183.

[13] 郭一鸣， 吴钟恺， 上官文斌. 衬套型橡胶悬置结构形状的优化方法[J]. 振动与冲击， 2022， 41（5）： 55-59.

GUO Y M， WU Z K， SHANGGUAN W B. Optimization method for the shape of bushing-type rubber suspension structure[J]. Vibration and Shock， 2022， 41（5）： 55-59.

[14] 邓雄志， 刘涛， 苏泽博. 轿车底盘橡胶衬套半经验设计方法研究[J]. 汽车技术， 2018（7）： 54-58.

DENG X Z， LIU T， SU Z B. Research on semi-empirical design method of rubber bushing in car chassis[J]. Automotive Technology， 2018（7）： 54-58.

[15] 史文库， 刘国政， 陈志勇. 橡胶的可压缩性在推力杆球铰有限元分析中的应用[J]. 西安交通大学学报， 2017， 51（9）： 63-68.

SHI W K， LIU G Z， CHEN Z Y. Application of rubber compressibility in the finite element analysis of thrust rod ball hinge[J]. Journal of Xian Jiaotong University， 2017， 51（9）： 63-68.

[16] 刘山尖， 孙伟星， 董兴建. 基于有限元模型的橡胶减振元件性能研究及失效分析[J]. 机电设备， 2014， 31（5）： 41-44.

LIU S J， SUN W X， DONG X J. Performance study and failure analysis of rubber vibration damping element based on finite element model[J]. Electromechanical Equipment， 2014， 31（5）： 41-44.

[17] KOSARAC A， MLADJENOVIC C， ZELJKOVIC M， et al. Neural-network-based approaches for optimization of machining parameters using small dataset[J]. Materials， 2022， 15（3）： 700.

[18] 陈静， 徐森， 刘震， 等. 基于碰撞安全性的铝合金吸能盒轻量优化[J]. 汽车工程， 2021， 43（2）： 241-247.

CHEN J， XU S， LIU Z， et al. Lightweight optimization of aluminium alloy energy absorption box based on crash safety[J]. Automotive Engineering， 2021， 43（2）： 241-247.

[19] ZHANG Z， LIAO C， CHAI H， et al. Multi-objective optimization of controllable configurations for bistable laminates using NSGA-Ⅱ[J]. Composite Structures， 2021， 266： 113764.

第一作者：秦武（1990—），男，讲师，博士，研究方向为橡胶隔振件性能分析及动力总成悬置系统设计。E-mail： qw@ ecjtu.edu.cn

通信作者：李春归（1999—），男，硕士研究生，研究方向为橡胶衬套性能分析。E-mail： 3047855129@qq.com