CRTS Ⅲ型板和双块式无砟轨道振动噪声特性研究

罗锟 王凯新 甄慧杰 陈鹏

收稿日期：2023-11-17

基金项目：国家自然科学基金项目（52178424，51868023）；江西省自然科学重点基金项目（20224ACB204018）；江西省科技专                     项（20223AEI91004）；江西省教育厅课题（GJJ2205122）；轨道交通基础设施性能监测与保障国家重点实验室自主课                   题（HJGZ2023207）

文章编号：1005-0523（2024）03-0029-08

摘要：【目的】探究高速铁路CRTS Ⅲ型板和双块式无砟轨道的结构振动与噪声特性。【方法】以有限元、多体动力学与边界元相结合的方法为基础，通过建立高速列车-无砟轨道-箱梁耦合动力学模型和边界元模型，研究列车高速通过时的列车-轨道-箱梁耦合系统的结构动力响应，以及噪声辐射特性。【结果】结果表明，列车通过桥上CRTS Ⅲ型板与双块式轨道结构段时，列车的最大轮重减载率分别为0.053 6与0.165 7，下部箱梁挠度分别为1/9 673与1/8 457。与双块式无砟轨道相比，CRTS Ⅲ型板的轨道板及底座位移响应更小，并且轨道-箱梁系统的竖向振动衰减更快，减振性能更优。另外，比较两种轨道结构条件下的高架箱梁结构噪声，CRTS Ⅲ型板段的箱梁噪声总声压级更小。但是，桥下远场点噪声峰值差异较小，峰值频率接近，均为31.5 Hz左右；而桥下峰值频率差异较大，Ⅲ型板的峰值频率为63 Hz，双块式则为20 Hz。【结论】CRTS Ⅲ型板式无砟轨道更适合在高速铁路桥梁段使用。

关键词：无砟轨道；箱梁；车-轨-桥耦合；振动；结构噪声

中图分类号：U211.3；U448.21+3 文献标志码：A

本文引用格式：罗锟，王凯新，甄慧杰，等. CRTS Ⅲ型板和双块式无砟轨道振动噪声特性研究[J]. 华东交通大学学报，2024，41（3）：29-36.

Investigation of Vibration and Noise Characteristics in CRTS Ⅲ Plate and Double-block Ballastless Track

Luo Kun1，2， Wang Kaixin1，2， Zhen Huijie1，2， Chen Peng1，2

（1. Engineering Research Center for Railway Environmental Vibration and Noise of the Ministry of Education， East China Jiaotong University， Nanchang 330013， China; 2. State Key Laboratory of Performance Monitoring Protecting of Rail Transit Infrastructure，East China Jiaotong University， Nanchang 330013， China）

Abstract： 【Objective】In order to explore the structural vibration and noise characteristics of high-speed railway CRTS Ⅲ type plates and double block tracks. 【Method】 Based on the method of finite element， multi-body dynamics and boundary element， the dynamic model and boundary element model of high-speed train-ballastless track-box girder coupling system are established to study the structural dynamic response and noise radiation characteristics of the train-track-box girder coupling system. 【Result】The results show that the maximum wheel load reduction rate of the train is 0.053 6 and 0.165 7， and the deflection of the lower box girder is 1/9 673 and 1/8 457， respectively， when the train passes the CRTS Ⅲ plate and the double-block track structure section on the bridge. Compared with the double-block ballastless track， the displacement response of the track plate and the base of the CRTS Ⅲ plate is smaller， and the vertical vibration attenuation of the track-box girder system is faster， and the vibration damping performance is better. In addition， the total sound pressure level of the box girder noise of CRTS Ⅲ segment is lower than that of the two types of track structure. However， the difference between the peak noise of the far field point under the bridge is small， and the peak frequency is similar， both of which are about 31.5 Hz. The peak frequency under the bridge has large differences， the peak frequency of type Ⅲ board being 63 Hz， and the double block type being 20 Hz.【Conclusion】CRTS Ⅲ plate type ballastless track is more suitable for use in high-speed railway bridge sections.

Key words： ballastless track; box girder; vehicle-rail-bridge coupling; vibration; structural noise

Citation format： LUO K， WANG K X， ZHEN H J， et al. Investigation of vibration and noise characteristics in CRTS Ⅲ plate and double-block ballastless track[J]. Journal of East China Jiaotong University， 2024， 41（3）： 29-36.

【研究意义】目前，我国新建高铁采用预制箱梁桥，主要选用CRTS Ⅲ型板与双块式无砟轨道。由于这两种轨道结构不同，列车通过时引起的振动响应也存在差异。因此，研究列车运行作用下，两种无砟轨道箱梁的动力响应，对于无砟轨道的结构选型，以及结构的振动噪声控制有着重要的工程价值。

【研究进展】对于轨道-桥梁结构的振动噪声研究，国内外已经取得了较为丰富的成果。李小珍等[1-3]针对高速铁路32 m预应力混凝土简支箱梁，开展现场锤击试验，探究箱梁的振动传递特性。以京沪高铁32 m简支梁桥为例，推导Oula-beinuli梁在任意移动荷载作用下的振动解析式，并研究不同参数对简支梁动力响应的影响。针对32 m单线和双线单室混凝土简支箱梁为研究对象，通过噪声试验、结构和声学有限元分析，研究箱梁结构噪声的声辐射特性、峰值频率产生的原因。张迅等[4-5]基于车-线-桥耦合振动和瞬态声辐射理论，研究混凝土箱梁低频结构噪声的数值预测，并分析结构噪声的时变特性。以32 m混凝土简支箱梁为研究对象，采用混合有限元-边界元法进行仿真，探讨了箱梁的结构噪声及其影响因素。张鹏飞等[6-7]以梁-板-桥相互作用原理为基础，运用有限元法建立桥上CRTS Ⅲ型板式无砟轨道无缝线路精细化空间耦合模型，研究了列车荷载作用长度及扣件支座对桥梁挠曲力与位移的影响。建立刚构桥无缝线路空间耦合模型，计算不同工况下轨道结构和桥梁的纵向力及位移，研究无缝线路的受力与变形。曾志平等[8]建立了普通轨道、中等减振扣件轨道、梯形轨枕轨道、钢弹簧浮置板轨道等4种不同类型的轨道结构有限元模型，分析了不同轨道在地铁荷载作用下振动传递规律，对地铁轨道设计、选型及优化设计提出了意见建议。杜淼[9]等通过建立有限元模型并结合功率流理论，建立桥梁声学边界元模型分析桥梁结构噪声特性，认为采用Ⅲ型板的桥梁降噪性能更优。

【创新特色】综上，虽然国内外学者对铁路桥梁进行了较多的现场实测，但主要针对的是桥梁响应以及CRTS Ⅱ型板式无砟轨道，尚缺乏对于无砟轨道结构动力响应的对比分析，使得轨道结构的动力选型问题仍困扰着铁路设计部门。因此，论文基于有限元法与多体动力学、边界元法，分析列车通过时，车、轨、桥的动力响应以及噪声特性。【关键问题】通过分析不同无砟轨道结构的声振特性，以期为高架轨道桥梁段的轨道结构选型及结构的减振降噪优化提供建议。

1 车-轨-桥耦合模型

目前我国高速铁路普遍采用以桥代路的建设形式，高架简支箱梁被大量投入使用。因此，以通桥（2023）2322A-Ⅱ预制简支箱梁为工程背景，建立有限元箱梁模型，箱梁尺寸如图1所示。

1.1 耦合模型的建立

我国新建高速铁路现阶段采用的箱梁，主要铺设CRTS Ⅲ型板式无砟轨道与双块式无砟轨道，轨道结构主要由钢轨、扣件、轨道板（道床板）、底座（支承层）等组成。钢轨采用梁单元、扣件，桥梁支座采用弹簧单元，其余结构采用实体单元模拟。主要材料参数及连接部件参数，如表1和表2所示[10-11]。

基于多体动力学[12-13]，导入轨道-箱梁有限元模型，建立列车-无砟轨道-箱梁耦合模型[14-16]，如图2所示，并采用中国高速铁路无砟轨道不平顺谱。

沿车辆前进方向，选取跨中截面作为分析截面。如图3所示，选取外侧钢轨（A1）、轨道板（A2）、底座（A3）、箱梁顶板（A4）和底板（A5）作为观测点，计算得到各观测点振动响应。为研究两种轨道箱梁结构噪声在不同场点辐射噪声的变化规律，选取桥下（S1～S5，距梁底的距离分别为2，4，6，8，10 m）、桥下远点（S6～S9，距箱梁中心线距离分别为5，10，15，20 m）共9处声场点，并进行倍频程声压级分析。

1.2 模型验证

采用文献[17]中的车-轨-桥结构参数，计算列车以300 km/h速度通过箱梁时的振动响应，得到跨中截面的顶板竖向振动加速度时程曲线，结果如图4（a）所示。与文献[17]的计算结果（图4（b））比较可知，振动加速度曲线趋势等吻合，证明本文建立模型的正确性。

2 结构动力响应分析

列车以300 km/h速度通过箱梁的时间约为2.8 s。列车要安全、平稳通过桥梁，并且轨道及桥梁的响应不会对列车运行产生不利影响。因此分析轮重减载率评价列车运行安全性，分析轨道结构的振动响应、桥梁的竖向挠度、振动传递率分析轨道结构的减振性能。

2.1 轮重减载率

在列车运行中发现，在横向力不大的情况下，轮重严重减载，也会出现脱轨现象，即当轮重偏载过大时，即便轮对横向力很小，也可能脱轨。目前我国建议的轮重减载率安全指标为

[危险限度ΔPP=P1-P2P1+P2=0.65允许限度ΔPP=P1-P2P1+P2=0.60] （1）

根据轮轨力进行计算，得到列车运行的轮重减载率，如表3所示。结果表明，列车运行在双块式轨道上时，轮重减载率最大值约为Ⅲ型板的3倍，即列车运行在Ⅲ型板上时，会更加安全。

2.2 轨道结构响应

提取轨道板（A2）及底座（A3）振动响应时域数据，如图5所示。

当列车通过箱梁时，双块式轨道板的振动位移明显大于Ⅲ型板，两者最大相差为0.145 mm；双块式轨道底座的振动位移同样大于Ⅲ型板，最大差值为0.15 mm。可能是道床板所采用材料的刚度低于轨道板所使用的材料导致。

2.3 桥梁挠度

提取箱梁跨中观测点（A4）振动响应数据，计算列车通过时的箱梁挠度，如表4所示。铺设两种轨道时，均能满足规范要求。并且，当铺设Ⅲ型板时，桥梁的竖向挠度更小。

2.4 竖向振动传递

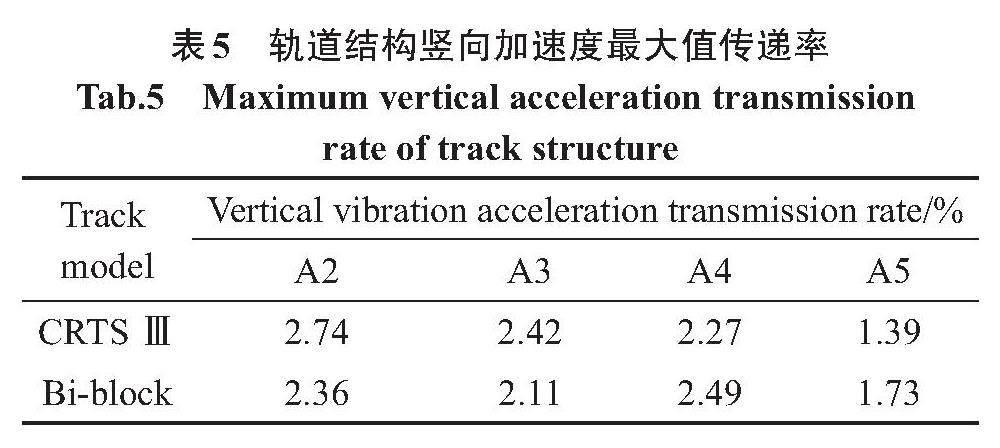
振动传播的系统包括多个子系统，在振源荷载的激励下，不同的子系统都会产生振动响应。而加速度是描述结构振动强度的关键性指标。因此提取钢轨（A1）振动加速度，与轨道板（A2）、底座（A3）、桥梁顶板（A4）与底板（A5）的振动加速度进行计算，如表5所示。

根据表5可知，振动从钢轨传递至轨道板（A2）、底座（A3）、箱梁顶板（A4）与底板（A5）的过程中，Ⅲ型板的传递率分别为2.74%，2.42%，2.27%与1.39%；而双块式的传递率则为2.36%，2.11%，2.49%与1.73%。计算结果表明，铺设Ⅲ型板时，桥梁顶板与底板的传递率更低，即Ⅲ型板的减振效果更好。

由于两种无砟轨道的结构及材料不同，导致Ⅲ型板在列车荷载作用下的振动响应更小，优于双块式轨道。并且Ⅲ型板的自密实混凝土，在兼顾一定的刚度的同时，仍具有一定的弹性，能在一定程度上减小振动的传递，增强结构的减振能力。

3 桥梁噪声分析

对于预应力混凝土桥梁，常采用边界元法，预测结构噪声。边界元法是边界积分方程的一种数值解法，基本思想是基于Green函数，采用Gauss定理把一个封闭区域上的积分转化为该区域边界上的积分[18]。

3.1 控制方程

假设在均匀介质、非黏性和绝热状态下，流体的声波声压波动方程为

[?2p=1c2?2p?t2]      （2）

式中：[?2=?2?x2+?2?y2+?2?z2]为Laplace算子。

场点Y，源点X，声波声压p的控制方程为三维波动方程

[?2p（Y，t）-1c2p（Y，t）=0]         （3）

式中：[pY，t]为声压对时间t的二阶导数。

设式（2）的基本解为[p*Y，t]，在空间域Q、时间域T内满足控制方程。通过声压势函数控制方程表示为

[?2p*Y，t-1c2p*（Y，t）=-γ（Y，t）]      （4）

式中：[γ（Y，t）]为空气波媒质的源密度函数，表示为

[γ（Y，t）=δ（t-τ）δ（Y-X）]  （5）

在声传播的边界[Γ]，利用[q=?p?n]，边界条件为

[q=-ρun]       （6）

式中：[ρ]为空气密度；[un]为结构面法向加速度。

利用delta函数，通过Laplace变化以及逆变换，计算声波时域的积分方程

[C（Y）P（Y，t）+Γ01q*Y，t;X，τP（X，τ）dτ dΓ]

[=Γ01P*Y，t;X，τq（X，τ）dτ dΓ] （7）

式中：边界形状的几何参数

[C（Y）=1-14πlimε→002π0φ（0）sinφdφdθ]    （8）

场点Y的声压基本解为

[P*0（Y，t;X，τ）=14πδ（t-rc-τ）]      （9）

对场点Y的声压基本解，在边界法向n求导，得到场点的声通量基本解

[p*0（Y，t;X，τ）=?P*（Y，t;X，τ）?n?]

[δ（t-rc-τ）+rcδ（t-rc-τ）?r?n]   （10）

通过有限元法，解得结构的振动响应，计算各节点声通量，进而得到所有节点声压

[Cnp+m=1nα=1nααmHn-m+1p（αδ）]

[=m=1nα=1nααmGn-m+1q（αδ）]     （11）

式中：[pn]为第n步各节点声压向量；[p（αδ）]为所有节点声压；[q（αδ）]为所有节点声通量的整体向量。

声场中各点声压[pn]为

[pn=-m=1nα=1nααmHn-m+1p（αδ）+]

[m=1nα=1nααmGn-m+1q（αδ）] （12）

式中：[ni=max1，n-nmax+1，nmax=rmaxcΔt+2]。

3.2 桥梁噪声特性

利用有限元计算结果，采用边界元方法，计算各场点声压，研究两种轨道结构箱梁结构噪声在不同场点辐射噪声的变化规律。

如图6（a）、图6（b）所示，采用Ⅲ型板的箱梁在桥下的声压级最大值均出现在63.0 Hz处，分别为84.1，80.6，78.5，77.7，76.9 dB，并且场点与箱梁底板的距离越远、噪声的幅值越小。但当场点的距离在6 m以上时，幅值间的差异极小。桥下远点的声压级最大值则出现在31.5 Hz处。而由图6（c）、图6（d）可知，采用双块式的箱梁在桥下的声压级最大值出现在20.0 Hz处，分别为82.7，81.4，80.1，79.0，77.7 dB，并且也出现随底板距离增大而减小的趋势，但幅值间的差异较小。桥下远点的声压级最大值也出现在31.5 Hz处。两种箱梁的桥下声压级，均在50.0 Hz处有明显的波谷，且最小值场点均为距箱梁底板6 m处的S3。

因此，采用两种轨道结构的箱梁，在桥下远点区域，其噪声特性差异较小。而在桥下区域，Ⅲ型板在63.0 Hz处噪声明显大于双块式，但在20.0 Hz处小于双块式。

并且，计算各场点噪声的总声压级，如图7所示。对于桥下的场点（S1～S5），总声压级大小为83.0～87.8 dB，并且能够明显发现，随场点距箱梁底板距离的增加，场点的总声压级越小。对于桥下远点（S6～S9），当场点不在箱梁的下方，即对于S7～S9场点而言，随场点与箱梁间距的增加，场点的总声压级越小。

在箱梁上铺设Ⅲ型板时，结构的振动小于双块式轨道，并且结构振动产生的结构噪声也小于双块式轨道。因此两种无砟轨道的噪声声压级特性相近，但Ⅲ型板的各场点声压及总声压级均小于双块式轨道。

4 结论

本文分别建立了使用CRTS Ⅲ型板式与双块式无砟轨道的车-轨-桥耦合模型以及声学边界元模型，研究了列车通过时，列车、轨道、箱梁结构的动力响应，以及桥梁噪声声压级特性，并进行对比分析，结果表明。

1） 当列车通过时，两种轨道结构都能满足列车快速且安全地运行，铺设Ⅲ型板时，列车运行会更稳定。并且由于两种无砟轨道所使用的材料不同，Ⅲ型板的振动位移明显小于双块式。

2） 铺设Ⅲ型板的箱梁，其动挠度会更小。同时，振动的竖向传递率也更小，Ⅲ型板的减振性能更加优越。

3） 采用Ⅲ型板与双块式的箱梁噪声声压级特性相近，均在50.0 Hz处有明显的波谷。Ⅲ型板的桥下噪声声压级峰值频率为63.0 Hz，而双块式为20.0 Hz。桥下远点的声压级峰值均为31.5 Hz，但噪声特性差异较小。采用Ⅲ型板的箱梁，各场点噪声总声压级，小于双块式轨道。

综上所述，Ⅲ型板的动力性能更优于双块式无砟轨道，而采用两种轨道结构的箱梁整体辐射噪声相近，故对于我国新建高速铁路更适宜选用CRTS Ⅲ型板式无砟轨道。

参考文献：

[1]    李小珍， 宋立忠， 张迅. 基于现场锤击试验的高铁简支箱梁振动传递特性研究[J]. 土木工程学报， 2016， 49（5）： 120-128.

LI X Z， SONG L Z， ZHANG X. Study on vibration transmission characteristics of high-speed railway simply-supported box-girders based on in-situ hammer excitation test[J]. China Civil Engineering Journal， 2016， 49（5）.120-128.

[2]    李小珍， 张志俊， 刘全民. 任意移动荷载列作用下简支梁桥竖向振动响应解析分析[J]. 振动与冲击， 2012， 31（20）： 137-142.

LI X Z， ZHANG Z J， LIU Q M. Vertical dynamic response analysis of a simply supported beam bridge under successive moving loads[J]. Journal of Vibration and Shock， 2012， 31（20）： 137-142.

[3]    李小珍， 张迅， 刘全民， 等. 铁路32 m混凝土简支箱梁结构噪声试验研究[J]. 中国铁道科学， 2013， 34（3）： 20-26.

LI X Z， ZHANG X， LIU Q M， et al. Experimental study on structure-borne noise of railway 32 m simply-supported concrete box-girder[J]. China Railway Science， 2013， 34， （3）： 20-26.

[4]    张迅， 李小珍， 宋立忠， 等. 铁路32 m混凝土箱梁结构噪声的时变特性研究[J]. 铁道学报， 2017， 39（6）： 20-26.

ZHANG X， LI X Z， SONG L Z， et al. Study on transient structure-borne noise radiated by 32 m-long railway concrete box-girder[J]. Journal of the China Railway Society，2017， 39（6）： 20-26.

[5]    张迅， 李小珍， 刘全民， 等. 混凝土箱梁的结构噪声及其影响因素[J]. 西南交通大学学报， 2013， 48（3）： 409-414.

ZHANG X， LI X Z， LIU Q M， et al. Structure-borne noise of concrete box-girder and its influence factors[J]. Journal of Southwest Jiaotong University， 2013， 48（3）：409-414.

[6]    张鹏飞， 桂昊， 雷晓燕， 等. 列车荷载下桥上CRTS Ⅲ型板式无砟轨道挠曲力与位移[J]. 交通运输工程学报， 2018， 18（6）： 61-72.

ZHANG P F， GUI H， LEI X Y， et al. Deflection force and displacement of CRTS Ⅲ slab track on bridge under train load[J]. Journal of Traffic and Transportation Engineering， 2018， 18（6）： 61-72.

[7]    张鹏飞， 黄安琪， 胡达贵， 等. 刚构桥上无砟轨道无缝线路静力特性分析[J]. 华东交通大学学报， 2023， 40（2）：30-38.

ZHANG P F， HUANG A Q， HU D G， et al. Comparative analysis on static characteristics of cwr of ballastless track on rigid frame bridge[J]. Journal of East China Jiaotong University， 2023， 40（2）： 30-38.

[8]    曾志平， 黄相东， 王卫东， 等. 地铁不同轨道类型振动传递规律对比研究[J]. 铁道工程学报， 2021， 38（7）： 74-79.

ZENG Z P， HUANG X D， WANG W D， et al. Comparative study on vibration transmission laws of different subway track types[J].Journal of Railway Engineering Society， 2021， 38（7）： 74-79.

[9]    杜淼， 王开云， 閤鑫， 等. 高速铁路典型无砟轨道的桥梁噪声特性分析[J]. 兰州交通大学学报， 2022， 41（6）： 89-95.

DU M， WANG K Y， HE X， et al. On noise characteristics of bridges with different ballastless tracks in high-speed railway[J] Journal of Lanzhou Jiaotong University， 2022， 41（6）： 89-95.

[10]  张鹏飞， 蔡科， 雷晓燕， 等. 地震作用下桥上CRTSⅢ型板式无砟轨道纵向动力响应分析[J]. 北京交通大学学报， 2023， 47（1）： 45-53.

ZHANG P F， CAI K， LEI X Y， et al. Longitudinal dynamic response analysis of CRTS Ⅲ slab track on bridge under seismic action[J]. Journal of Beijing Jiaotong University， 2023，47（1）： 45-53.

[11]  闫斌， 黄杰， 谢浩然， 等. 连续梁桥上CRTS双块式无砟轨道疲劳特性[J]. 哈尔滨工业大学学报， 2023， 55（7）：52-59.

YAN B， HUANG J， XIE H R， et al. Fatigue characteristics of CRTS bi-block ballastless track on continuous bridge of high-speed railway[J]. Journal of Harbin Institute of Technology， 2023， 55（7）： 52-59.

[12]  宋攀. 高速列车-简支梁桥耦合振动仿真分析[D]. 石家庄： 石家庄铁道大学， 2019.

SONG P. Coupled vibration simulation analysis of high speed train-simply supported beam bridge[D]. Shijiazhuang： Shijiazhuang Tiedao University， 2019.

[13]  XIN Z， SHUANG C H， PENG Z， et al. On the modelling of normal wheel-rail contact for high-frequency vehicle-track dynamics analyses[J]. International Journal of Rail Transportation， 2022， 10（6）： 695-716.

[14]  翟婉明. 车辆-轨道耦合动力学理论的发展与工程实践[J]. 科学通报， 2022， 67（32）： 3794-3807.

ZHAI W M. Development of vehicle-track coupled dynamics theory and engineering practice[J]. Chinese Science Bulletin， 2022， 67（32）： 3794-3807.

[15]  ZHAI W M， WANG K Y， CAI C B. Fundamentals of vehicle-track coupled dynamics[J]. Vehicle System Dynamics， 2009， 47（11）： 1349-1376.

[16]  XIN L， LI X， ZHANG J， et al. Resonance analysis of train-track-bridge interaction systems with correlated uncertainties[J]. International Journal of Structural Stability and Dynamics， 2020， 20（1）： 2050008.

[17]  雷晓燕， 王鹏生， 翁凌霄， 等. 时速300 km高速列车诱发高架箱梁结构振动特性分析[J]. 华东交通大学学报， 2021， 38（4）： 18-26.

LEI X Y， WANG P S， WENG L X， et al. analysis of vibration characteristics of box girder structure induced by high-speed train at 300 km[J]. Journal of East China Jiaotong University， 2021， 38（4）： 18-26.

[18]  吴海军. 基于快速多极子边界元方法的大规模声学计算方法与应用研究[D]. 上海： 上海交通大学， 2013.

WU H J. Study on computational methods and applications for large scale acoustic problems based on the fast multipole boundary element method[D]. Shanghai： Shanghai Jiao Tong University， 2013.