车桥耦合振动下损伤连续梁桥承载力评定方法研究

亓兴军 佀贞贞 李淑堃 郭冬梅

收稿日期：2023-10-11

基金项目：山东省交通运输厅科技计划项目（2022B06）；山东省企业技术创新项目（202250101726，202160101415）

文章编号：1005-0523（2024）03-0045-10

摘要：【目的】桥梁的安全与承载能力至关重要，为简化试验流程、提高检测效率，以实际工程中一座两跨连续梁桥为研究背景，基于移动车辆进行轻荷载数值分析，探究车桥耦合振动下损伤桥梁承载力评定方法的准确性与可行性。【方法】建立车桥耦合振动模型，提取桥梁结构控制截面的挠度、应变动态时程响应，利用经验模态分解（EMD）和变分模态分解（VMD）去除动力成分并识别准静态响应曲线，分析桥面粗糙度和车速对准静态响应识别精度的影响；通过车辆行驶中控制截面产生的不同响应计算不同加载位置的加载效率，利用“常丁模型”计算轻荷载效率下损伤桥梁控制截面准静态响应的标准校验系数，对损伤连续梁桥的承载力进行评估。【结果】相较于EMD，VMD分解的准静态响应曲线与静态响应曲线吻合程度更好；随着桥面粗糙度、加载车辆移动速度的增大，识别的准静态响应与静态响应的误差也逐步增大；移动车辆加载过程中识别的准静态响应较为精确，可作为静载实测值进行计算；计算的标准校验系数均大于1，准确评估了桥梁的损伤状态。【结论】基于车桥耦合振动评估损伤桥梁承载力的方法具有较强的适用性和可行性。

关键词：车桥耦合；承载力评估；准静态响应；轻荷载；粗糙度；损伤；振动；连续梁桥

中图分类号：U446 文献标志码：A

本文引用格式：亓兴军，佀贞贞，李淑堃，等. 车桥耦合振动下损伤连续梁桥承载力评定方法研究[J]. 华东交通大学学报，2024，41（3）：45-54.

Research on the Bearing Capacity Evaluation Method of Damaged Continuous Beam Bridge under Vehicle-Bridge Coupling Vibration

Qi Xingjun， Si Zhenzhen， Li Shukun， Guo Dongmei

（School of Transportation Engineering Shandong Jianzhu University， Jinan 250101， China）

Abstract： 【Objective】In order to simplify the test process and improve the detection efficiency， a two-span continuous beam bridge in the actual project was taken as the research background， and the light load numerical analysis was carried out based on the moving vehicle， and the accuracy and feasibility of the evaluation method of the damaged bridge bearing capacity under vehicle-bridge coupling vibration were explored. 【Method】The vehicle-bridge coupling vibration model was established， the deflection and strain dynamic time-history response of the control section of the bridge structure were extracted， the dynamic components were removed by empirical mode decomposition （EMD） and variational mode decomposition （VMD） and the quasi-static response curve was identified， and the influence of bridge deck roughness and vehicle speed on the accuracy of the static response recognition was analyzed. The loading efficiency of different loading positions was calculated by the different responses of the control section during vehicle driving， and the standard check coefficient of the quasi-static response of the control section of the damaged bridge under light load efficiency was calculated by using the “Changding model”， and the bearing capacity of the damaged continuous beam bridge was evaluated.【Result】Compared with EMD， the quasi-static response curve of VMD decomposition is in better agreement with the static response curve. With the increase of bridge deck roughness and the moving speed of the loading vehicle， the error of the recognized quasi-static response and the static response also gradually increases. The quasi-static response identified during the loading process of the moving vehicle is relatively accurate and can be calculated as the measured value of static load. The calculated standard check factors are all greater than 1， which accurately evaluates the damage state of the bridge. 【Conclusion】It is highly applicable and feasible to evaluate the bearing capacity of damaged bridges based on vehicle-bridge coupling vibration.

Key words： vehicle axle coupling; assessment of bearing capacity; quasi static response; light load; roughness; damage; vibration; continuous girder bridge

Citation format： QI X J， SI Z Z， LI S K， et al. Research on the bearing capacity evaluation method of damaged continuous beam bridge under vehicle-bridge coupling vibration[J]. Journal of East China Jiaotong University， 2024， 41（3）： 45-54.

【研究意义】桥梁在运营期间受到人为或复杂环境等因素影响时容易产生结构疲劳和材料老化问题，导致正常使用荷载和抵抗自然灾害的能力下降，对桥梁的安全构成威胁。为减少桥梁灾害的发生，需要对在役桥梁的安全状况和承载能力进行快速有效评估[1-3]。

【研究进展】静载试验[4]作为一种最直接有效评估桥梁承载力的方法，得到普遍采用。叶青[5]进行现场静载试验，对车辆荷载作用下简支变连续小箱梁的应力、挠度变化进行了研究；张新志[6]提出了一种以数值模拟为基础并结合静载试验的方法，对旧桥承载能力进行评定。但由于静载试验需要中断交通，且试验过程繁琐，费时费力，因此在中小桥梁承载力快速评估中很难广泛应用[7-8]。

准静态响应通过移动荷载下桥梁结构的振动得出，对于结构的特殊截面可任意地施加荷载，相比于传统静载试验，避免了工况少、数据少的缺点[9]。Wang等[10]提出一种从车辆行驶引起的动力响应中提取桥梁影响线的拟合方法，采用车桥模型的数值算例对该方法进行验证，证明了快速评定桥梁承载力的可行性；Brien等[11]建立了与加载车辆相关的矩阵，通过求矩阵的逆并建立方程组从桥梁实测响应中直接提取桥梁影响线；史文军[12]通过在桥上布置移动荷载，利用准静态响应修正有限元模型，实现了对桥梁的承载力评估；林迪南[13]根据常丁轻荷载试验[14]的回归模型以及实测数据，将移动车辆荷载与动挠度影响线相结合，对桥梁承载力进行了快速评定；王珊珊等[15]采用一辆加载跑车，基于轻荷载试验实现桥梁承载力的快速评估，提高了检测效率。

【创新特色】一方面，上述研究均在车辆缓慢行驶的状态下进行，耗时长且工作效率低，而运用车桥耦合理论可以获得车辆在正常行驶速度下桥梁的动力响应；另一方面，由于轻荷载试验流程简便、完成速度快，且工作效率高、节省了人力物力等资源，已成为快速评估桥梁承载力的新的研究方向[14]。因此，本文将车桥耦合理论与轻荷载试验相结合，探究一种快速评定损伤桥梁承载能力的新方法。【关键问题】基于实际工程中的一座两跨连续梁桥，建立不同桥面粗糙度、不同车辆行驶速度的车桥耦合数值有限元模型，提取各个工况下损伤桥梁控制截面的挠度和应变时程响应，对比桥梁静态响应，探究桥梁准静态响应识别的影响因素，并说明移动车辆加载过程中识别桥梁准静态响应的可行性；通过车辆行驶中控制截面产生的不同响应模拟不同加载效率下的多个静载试验工况，根据常丁轻荷载计算方法[14]，对车桥耦合振动下的损伤连续梁桥承载力进行快速评估。

1 基本原理

1.1 车桥耦合振动理论

近年来，学者们采用数值模拟法对车桥耦合的动力特性进行了大量研究。通常使用刚体动力学方法来构建车辆模型，建立桥梁的有限元模型，将车辆与桥梁模型分别看作两个子系统，利用车轮与桥面之间的位移协调、相互作用力大小相等的关系，将两个子系统的动力方程联系起来，采用迭代法对系统响应结果进行求解[16-17]。基于此建立车桥耦合振动模型，提取移动车辆下的桥梁动力响应。

1.2 轻荷载下桥梁承载力评估

荷载试验校验系数是指在加载过程中，实测的弹性变位（或应变）值与理论计算变位（或应变）值的比值。从形式上看，变位（或应变）值可以转换为刚度值，则校验系数也可由实测抗弯刚度与理论抗弯刚度的比值来定义。若结构处于线弹性范围内，则校验系数为常数，不受车辆荷载大小及位置的影响；但对桥梁进行荷载试验时，实际荷载效率会随外荷载的递增而发生变化，外荷载递增相当于分级加载，所以每级荷载加载工况下，加载效率与校验系数间均存在一定的函数关系，且标准荷载与轻荷载下的校验系数之间也存在一定的函数关系[15]。

在分析校验系数的关系中，0.3～0.85的荷载效率分为5个档次范围，分别为0.3～0.44，0.45～0.54，0.55～0.64，0.65～0.74，0.75～0.84。以荷载效率作为分类标准，采用做差值的方法分析，对重荷载与所划分的轻荷载下的校验系数进行计算

[Δa=ζ-ζn]              （1）

[Δr=ζ-ζnζn]              （2）

式中：[Δa]为绝对差值；[Δr]为相对差值；[ζ]为在荷载效率0.85～1.05内的应变（或挠度）校验系数；[ζn]为在5个低荷载效率范围内的应变（或挠度）校验系数；n=1～5。

常丁[14]通过对103座中小跨径桥梁（预应力混凝土桥66座，钢筋混凝土桥37座）荷载试验的分级加载数据统计分析，得出钢筋混凝土梁桥的校验系数差值范围及相对差值-对应荷载效率回归方程（[Δr-η]回归方程），将该回归关系称为“常丁模型”，如表1、表2所示。在此基础上，根据轻荷载的加载效率便可推算出标准荷载下结构的标准校验系数，结合规范对桥梁承载力进行评估。

根据《公路桥梁承载能力检测评定规程》（JTG/T J21—2011），校验系数是评定桥梁承载能力的一项重要指标，其计算式如下

[ζ=SeSs]                 （3）

式中：[Se]为试验荷载作用下结构的实测挠度（或应变）值；[Ss]为试验荷载作用下结构的理论挠度（或应变）值。当[ζ]=1时，说明理论值与实测值完全相符；当[ζ]<1时，表明桥梁的受力性能良好，结构的承载能力充足；当[ζ]>1时，表明桥梁的受力性能较差，结构的承载能力不足。

2 模型参数

为准确获得车辆激励下桥梁的动力响应，基于分离法与车辆动力学原理，建立车辆与桥梁耦合振动的有限元模型[18]；通过双轴半车模型模拟实测车辆，使其以不同速度驶过不同等级粗糙度的桥面，提取梁桥结构控制截面的挠度与应变时程响应并展开分析。控制截面根据设计荷载下弯矩的正负最大值得出，包括第一跨跨中截面、桥墩支点截面、第二跨跨中截面。

2.1 桥梁模型

桥梁模型以实际工程中一座跨径为15.41 m+15.41 m两跨钢筋混凝土连续板桥建立，桥梁横断面图如图1所示。梁高0.8 m，桥面宽度为4.9 m，横断面组合为0.45 m（护栏）+4.0 m（车行道）+0.45 m（护栏）=4.9 m；桥梁顶面预留0.2 m铺装。

依据连续梁桥竣工图纸建立有限元模型，全桥主梁为[C40]预应力混凝土，采用[BEAM4]单元模拟，单元长度为0.05 m，材料弹性模量为3×1010 [Pa]、泊松比取0.2、密度为2 600[kg/m3]；桥面铺装采用[MASS21]质量单元模拟，直接附加到主梁单元上；支座约束为3个竖向约束、3个横向约束、3个顺桥向转动约束及1个纵向约束；建立的连续梁桥有限元模型如图2所示。

2.2 车辆模型

假定车辆系统为刚体，仅在平衡位置产生微小振动且只承受竖向力，车辆匀速行驶通过不平整桥面，并与桥梁始终紧密接触，无跳起现象。悬挂系统阻尼通过弹簧模拟，双轴半车动力学模型如图3所示。

图3中：M=3.85×104 kg，为车体的质量；[Kai]=4.28×106 N/m，[Cai]=9.8×104 kg/s，分别为连接车体与悬挂系统之间的弹簧刚度，阻尼系数；[Kbi]=2.535×106 N/m，[Cbi]=1.96×105 kg/s，分别为车辆悬架系统与轮对的弹簧刚度，阻尼系数；[mi]=4 330 kg，为车辆悬挂系统与轮对的质量之和；L=5 m，为车体前后轴之间的距离；[Ia]=2.466×106 kg?m2，为车体绕横轴的转动惯量；i=1，2。

3 准静态响应识别

提取桥梁时程响应后，利用预处理方法将其动力成分去除，转化为准静态时程响应。经验模态分解（EMD）是在时频域中，不需要事先设置基函数，只需根据数据本身的时间尺度特征对其进行信号分解的一种处理方法[19]。变分模态分解（VMD）是由Dragomiretskiy等[20]提出的一种信号处理方法；其分解过程可归纳为对原始信号进行筛选，将具有频域优势的信号分解成一组调幅和调频信号。

为验证识别的准静态响应用于评估桥梁承载能力的可行性，建立连续梁桥损伤模型，分别采用EMD、VMD识别损伤桥梁各控制截面的挠度和应变准静态响应，分析桥面粗糙度和车速对识别结果的影响。

3.1 损伤模拟

在实际工程中结构的损伤，如裂缝、材料性能退化等，一般会引起结构刚度产生较大的变化，而对结构的质量影响较小。因此，在有限元计算中，假定结构单元损伤只降低单元刚度，而不引起单元质量的改变[21]。单元的损伤通过降低弹性模量来模拟，其中，第一跨跨中截面（单元155）损伤20%，桥墩支点截面（单元310）损伤30%。准静态响应测点包括第一跨跨中截面挠度和应变，桥墩支点截面应变，第二跨跨中截面挠度和应变。

3.2 粗糙度对准静态响应识别的影响

桥面粗糙度是车桥耦合振动的重要影响因素，不平整的桥面将加剧车辆的振动，从而引起桥梁结构更大的响应。

桥面（路面）粗糙度等级按照功率谱密度可以分为A～H共8级，前3个等级A、B、C如表3所示。

31 m长桥面粗糙度模拟如图4所示。

为探究不同粗糙度对准静态响应识别的影响，分别对桥面施加A、B、C级粗糙度，建立车桥耦合模型进行计算；车辆分别以0.001，30 km/h的速度行驶过桥，v=0.001 km/h时产生的时程响应被视为桥梁静态响应。

以车辆前轴作用位置为横坐标，分别利用EMD、VMD来分解含动力扰动的梁桥挠度、应变时程响应，预处理后的准静态响应如图5～图9所示。因采用车辆前轴上桥、后轴下桥的行驶过桥模型，故图中横坐标范围为36 m。

考虑车辆多轴效应，1/2双轴车位于连续梁桥跨中附近的应变时程响应曲线存在“平台”，其长度等于车辆轴距。

由图5～图9可知，基于EMD、VMD预处理得到的控制截面挠度时程响应曲线峰值的绝对值随着桥面粗糙度的增大而降低，而应变时程响应曲线峰值随之增大；且挠度与应变响应曲线随桥面粗糙度的增大与桥梁静态曲线吻合程度降低。

两种预处理方法得到的准静态响应曲线与静态响应曲线均吻合较好，但相较于VMD，EMD预处理的准静态时程响应曲线仍存在微小波动，这是由于EMD初设筛选条件与时程响应曲线形状，导致挠度与应变时程响应中的IMF未被完全识别；而基于VMD的桥梁时程响应预处理方法可有效剔除响应中的动力成分，得到较为光滑的准静态响应曲线。

3.3 车速对准静态响应识别的影响

为了更加切合实际，在桥面施加C级粗糙度，车辆移动荷载分别以0.001，10，30，50，72 km/h速度过桥。其中车辆以0.001 km/h速度过桥产生的时程响应被视为桥梁静态响应。

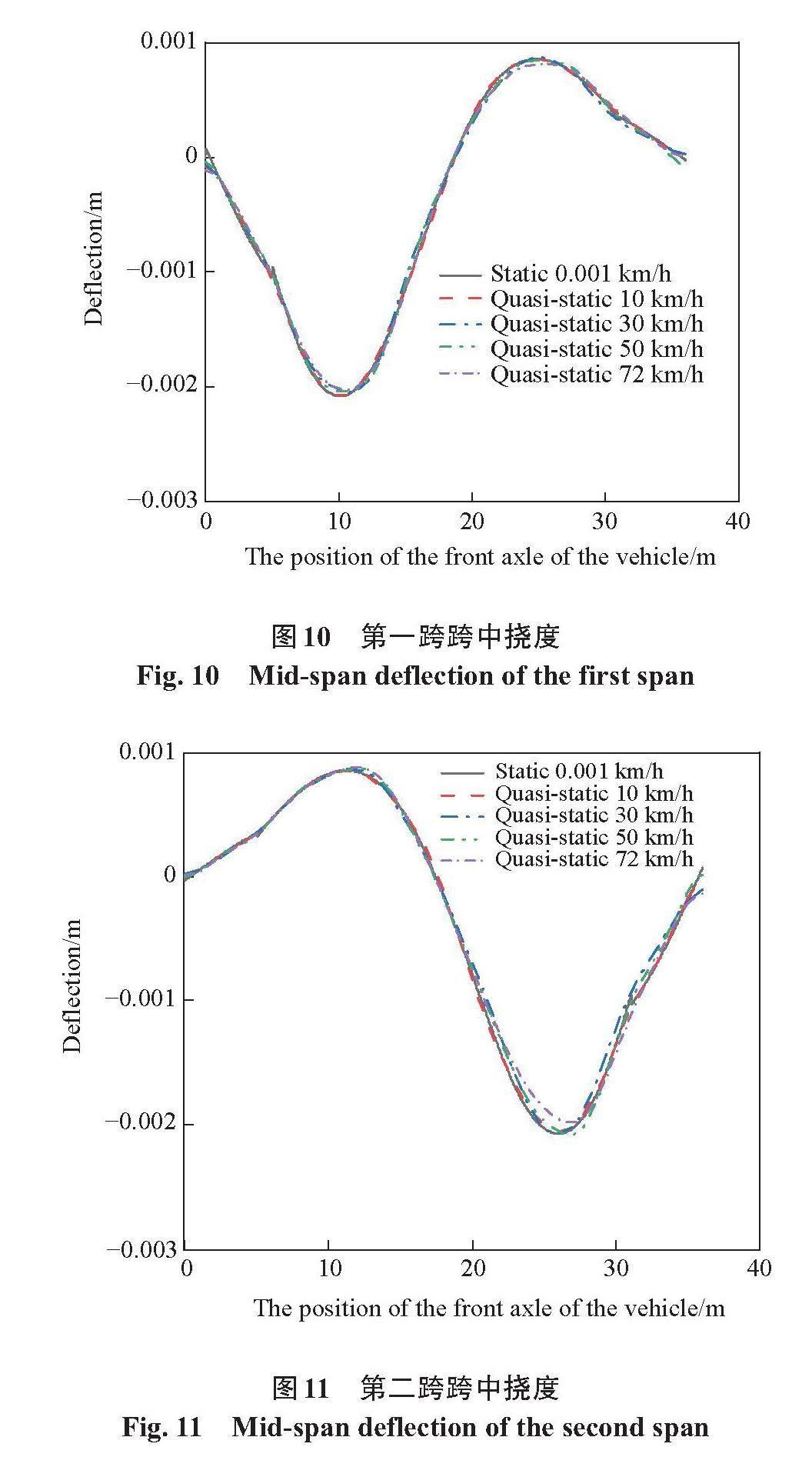
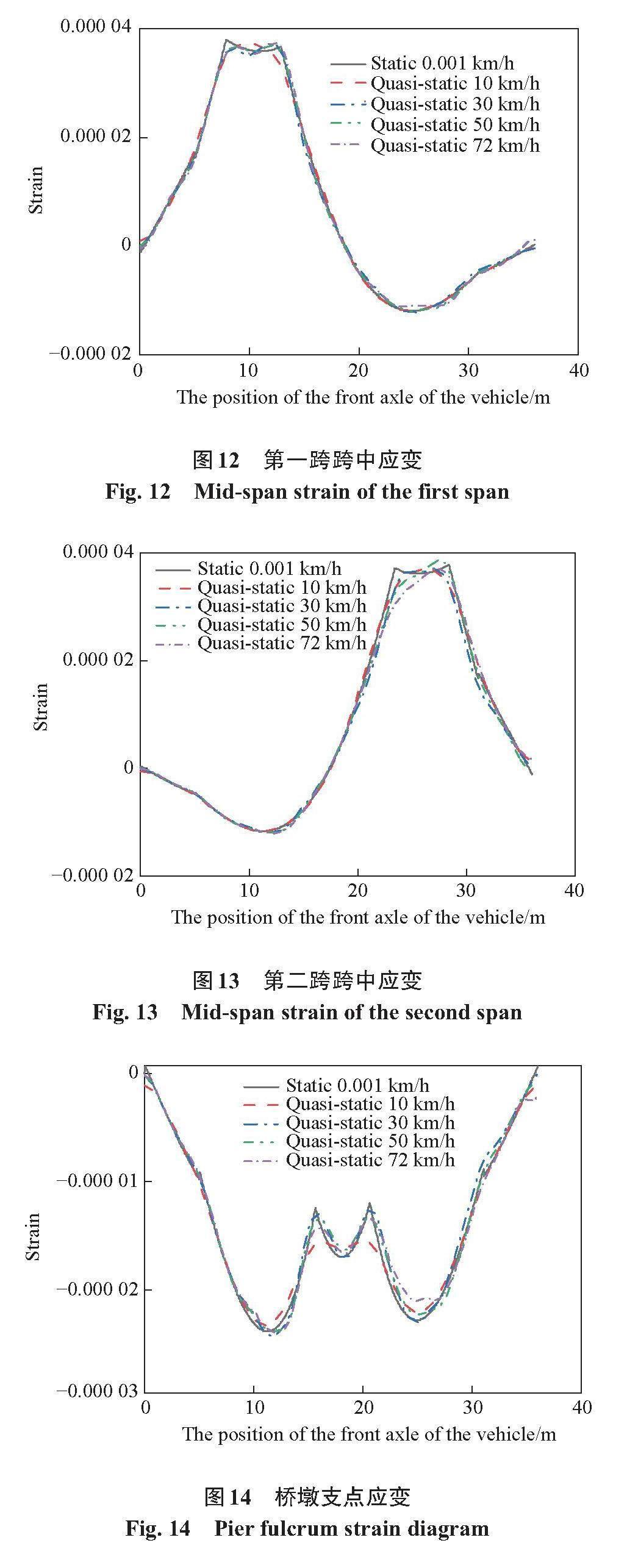
以车辆前轴作用位置为横坐标，采用识别效果较好的VMD来分解含动力扰动的梁桥挠度、应变时程响应，预处理后的准静态响应见图10～图14。

由图10～图14可知，基于VMD的桥梁时程响应预处理方法可有效剔除各车辆速度下连续梁桥控制截面挠度与应变响应中的动力成分，但挠度与应变响应曲线随加载车辆移动速度的增大与桥梁静态曲线吻合程度降低。由于行驶车辆的双轴效应，在车辆行驶通过跨中截面时，应变响应曲线出现“平台”段。

随加载车辆移动速度的增大，基于VMD预处理得到的跨中挠度时程响应曲线峰值的绝对值整体下降，跨中应变时程响应曲线峰值增大；而桥墩支点应变曲线峰值随车辆移动速度的增大而减小，但当移动加载车辆速度为10 km/h时，因时程响应中振动响应较小，经VMD预处理得到的准静态曲线峰值也较小。

综上，相较于EMD，VMD分解的准静态响应与静态响应吻合程度更好；挠度与应变准静态响应曲线随桥面粗糙度、加载车辆移动速度的增大与桥梁静态响应曲线的拟合误差也逐步增大；v=10 km/h情况下，由于振动响应较小，导致峰值也相对较小，与桥梁静态曲线吻合程度较低；响应识别应在贴合实际的情况下，选择合适的车速及桥面粗糙度；车桥耦合振动测试下识别的准静态响应较为精确，可作为静载实测值计算桥梁加载效率和校验系数，对桥梁承载力进行评估。

4 基于准静态响应的桥梁承载力评定

4.1 加载效率计算

采用公路-Ⅱ级车道荷载进行加载，车道荷载由均布荷载和集中荷载组成。根据桥规规定，公路-Ⅱ级车道荷载的均布荷载为7.785 kN/m，集中荷载为218.250 kN。

利用完好桥梁跨中弯矩的影响线确定设计荷载中最不利荷载的加载位置。加载效率[ηq]计算式如下

[ηq=SsS（1+μ）]               （4）

式中：[Ss]为静力荷载试验作用下，某一加载试验项目对应的加载控制截面内力、应力或变位的最大计算效应值；[S]为控制荷载产生的同一加载控制截面内力或位移的最不利效应设计值；[μ]为按规范取定的冲击系数值。

通过车辆行驶过程中控制截面产生的不同响应模拟不同加载位置时的多个静载试验工况，桥梁每跨等分10个加载位置放置车辆前轴荷载，全桥共20个加载位置，计算每个工况下完好桥梁各控制截面准静态响应的加载效率，见表4。

由表4可知，全程加载效率在0.30～0.85之间，其中，0.30～0.84为轻荷载效率，可采用钢筋混凝土板桥的[Δr-η]回归方程进行计算转换；0.85时满足加载效率。

4.2 承载力评定

计算车辆荷载作用下桥梁的校验系数（轻荷载效率时利用“常丁模型”计算转变为满足加载效率的标准荷载试验校验系数），结合现行规范对该损伤连续梁桥的承载力进行快速评估。

根据车辆轴重，将车辆荷载等效为集中力分配到连续梁桥初始有限元模型节点上，计算相应实测测点的理论静力挠度和应变；根据控制截面测点的理论值与实测值，计算全桥20个加载位置时损伤桥梁各控制截面准静态响应的挠度和应变校验系数。实际工程中桥面为沥青铺装，且桥面越粗糙，准静态响应曲线与静态响应曲线吻合程度越低。因此，为贴合实际状况，仅对C级桥面粗糙度进行分析，由于篇幅关系，选取车速v=10 km/h及v=50 km/h下的挠度和应变准静态响应进行计算。由计算结果可知，两个速度下第一跨跨中截面的挠度校验系数分布范围为0.93～1.09，应变校验系数分布范围为0.90～1.07；两个速度下第二跨跨中截面的挠度校验系数分布范围为0.89～1.10，应变校验系数分布范围为0.89～1.17；两个速度下桥墩支点截面的应变校验系数分布范围为0.83～1.08。

根据轻荷载加载效率及校验系数差值回归方程，将轻荷载效率下的校验系数转变为满足荷载效率0.85～1.05下的标准校验系数，转变后控制截面的挠度及应变标准校验系数分布范围及平均值如表5所示。

由表5可知，由轻荷载下校验系数转变为标准荷载下校验系数后，各测点的挠度及应变校验系数范围为0.86～1.37，说明桥梁整体结构处于弹性工作状态，对各控制截面的挠度和应变标准校验系数取平均值，各标准校验系数均值均大于1，表明连续梁桥模拟损伤后的承载力不满足要求，符合损伤模型工作状况。

6 结论

1） 相比EMD识别法，基于VMD的预处理方法可有效剔除各影响变量下连续梁桥控制截面挠度与应变响应中的动力成分，得到较为光滑的准静态挠度与应变曲线，且与静态响应吻合程度较好。

2） 各响应准静态曲线与静态曲线的误差随桥面粗糙度、加载车辆移动速度的增大而增大，因此响应识别应选择合适的车速及桥面粗糙度。

3） 各工况下控制截面的挠度、应变准静态响应曲线与静态曲线吻合程度良好，移动车辆加载过程识别的准静态响应较为精确，可作为静载实测值计算桥梁加载效率和校验系数，进而评定桥梁承载能力。

4） 由“常丁模型”计算的标准校验系数平均值均大于1，表明该连续梁桥的承载力不满足要求，与损伤模型模拟情况相吻合，证明了基于车桥耦合振动测试方法评定桥梁承载能力的有效性和工程可行性。

参考文献：

[1]   贺拴海， 赵祥模， 马建， 等. 公路桥梁检测及评价技术综述[J]. 中国公路学报， 2017， 30（11）： 63-80.

HE S H， ZHAO X M， MA J et al. Review of highway bridge inspection and condition assessment[J]. China Journal of Highway and Transport， 2017， 30（11）： 63-80.

[2]   刘旭政， 汤仲训， 贾丽华， 等. 桥梁荷载试验车辆自动化布载程序对比分析[J]. 沈阳建筑大学学报（自然科学版）， 2021， 37（1）： 113-120.

LIU X Z， TANG Z X， JIA L H， et al. Comparison and analysis on testing vehicle automatic layout program for bridge load test[J]. Journal of Shenyang Jianzhu University （Natural Science）， 2021， 37（1）： 113-120.

[3]   ALIASGHAR M M， KOUTROMANOS I， ROBERTS W C， et al. Analytical evaluation of corrosion-induced strength degradation in prestressed bridge girders[J]. Journal of Structural Engineering， 2022， 148（11）： 1-16.

[4]   张茵涛. 在役预应力混凝土梁桥静载试验[J]. 铁道建筑， 2018， 58（3）： 28-30.

ZHANG Y T. Static load test study on prestressed concrete girder bridge in service[J]. Railway Engineering， 2018， 58（3）： 28-30.

[5]   叶青. 简支变连续小箱梁桥单梁静载试验研究[J]. 北方交通， 2017（10）： 15-18.

YE Q. Research on static load test for single girder of simple support-continuous small box girder bridge[J]. Northern Communications， 2017（10）： 15-18.

[6]   张新志. 钢筋混凝土旧桥承载能力评估方法研究[J]. 公路， 2013（1）： 274-277.

ZHANG X Z. Research on evaliation method of carrying capacity of reinforced concrete old bridge[J]. Highway，2013（1）： 274-277.

[7]   李东平， 唐新葵， 王宁波. 基于实际影响线的桥梁快速检测方法[J]. 桥梁建设， 2019， 49（1）： 42-46.

LI D P， TANG X K， WANG N B. Bridge rapid detection method based on actual influence line[J]. Bridge Construction， 2019， 49（1）： 42-46.

[8]   张劲泉， 李鹏飞， 董振华， 等. 服役公路桥梁可靠性评估的若干问题探究[J]. 土木工程学报， 2019， 52（S1）： 159-173.

ZHANG J Q， LI P F， DONG Z H， et al. Study on some reliability evaluation problems of existing highway bridges [J]. China Civil Engineering Journal， 2019， 52（S1）： 159-173.

[9]   李贤东. 基于准静态广义影响线的双曲拱桥承载力评定初步研究[D]. 重庆： 重庆交通大学， 2009.

LI X D. Study on some reliability evaluation problems of existing highway bridges[D]. Chongqing： Chongqing Jiaotong University， 2009.

[10] WANG N B， HE L X， REN W X， et al. Extraction of influence line through a fitting method from bridge dynamic response induced by a passing vehicle[J]. Engineering Structures， 2017， 151： 648-664.

[11] BRIEN E J， QUILLIGAN M J， KAROUMI R. Calculating an influence line from direct measurements[J]. Proceedings of the Institution of Civil Engineers-Bridge Engineering， 2006， 159（1）：721-743.

[12] 史文军. 基于准静态影响线的桥梁承载能力评估方法研究[D]. 天津： 河北工业大学， 2012.

SHI W J. Study of the bridges carrying capacity evaluation method based on the quasi-static influence line[D]. Tianjin： Hebei University of Technology， 2012.

[13] 林迪南. 基于实时监测的混凝土梁桥安全性能快速评估方法研究[D]. 南京： 东南大学， 2016.

LIN D N. Study of fast safety assessment of conerete girder bridge based on real time monitoring[D]. Nanjing：Southeast University， 2016.

[14] 常丁. 基于轻荷载试验梁桥承载力快速评定研究[D]. 西安： 长安大学， 2010.

CHANG D. Studies on light-load test method for rapid evaluation research of beam bridge loading capacity[D]. Xi'an： Chang'an University， 2010.

[15] 王珊珊， 张荣凤， 亓兴军， 等. 基于影响线轻荷载试验的桥梁承载力评估方法研究[J]. 施工技术（中英文）， 2022， 51（12）： 13-18.

WANG S S， ZHANG R F， QI X J， et al. Evaluation method of bridge bearing capacity based on light-load test of influence line[J]. Construction Technology， 2022， 51（12）： 13-18.

[16] 陈水生， 葛世祺， 桂水荣， 等. 基于车桥耦合振动的公路梁桥行车舒适性分析[J]. 华东交通大学学报， 2023， 40（1）： 1-9.

CHEN S S， GE S Q， GUI S R， et al. Analysis on driving comfort of highway beam bridge based on vehicle-bridge coupling vibration[J]. Journal of East China Jiaotong University， 2023， 40（1）： 1-9.

[17] 吴大宏， 屠嘉杨， 苏伟， 等. 车桥耦合振动高速铁路典型桥梁动力系数研究[J]. 华东交通大学学报， 2022， 39（2）： 17-26.

WU D H， TU J Y， SU W， et al. Study on the dynamic coefficient law of typical bridges of highspeed railway based on vehicle-bridge coupling vibration[J]. Journal of East China Jiaotong University， 2022， 39（2）： 17-26.

[18] 刘世忠. 双层公路钢桁梁桥车桥耦合振动研究[D]. 西安： 长安大学， 2015.

LIU S Z. Research on vehicle-bridge coupled vibration of double-deck highway steel truss bridge[D]. Xi'an： Chang'an University， 2015.

[19] 邹云峰， 付正亿， 何旭辉， 等. 基于经验模态分解和模型缩聚的动力响应重构方法研究[J]. 工程力学， 2022， 39（2）： 67-75.

ZOU Y F， FU Z Y， HE X H， et al. Dynamic response reconstruction method based on empirical mode decomposition and model condensation[J]. Engineering Mechanics， 202， 39（2）： 67-75.

[20] DRAGOMIRETSKIY K， ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing， 2014， 62（3）： 531-544.

[21] CAWLEY P， ADAMS R D. The location of defects in structures from measurements of natural frequencies[J]. Journal of Strain Analysis， 1979（2）： 49-57．

第一作者：亓兴军（1974—），男，教授，博士，研究方向为桥梁健康监测与抗震防灾。E-mail：qxj123@163.com。