直观蕴涵本质 关联完善建构

那文君

1 试题呈现

（2022年南京中考·27）在平面内，先将一个多边形以自身的一个顶点为位似中心放大和缩小，再将所得多边形沿过该点的直线翻折，我们称这种变化为自位似轴对称变换，变换前后的图形成自位似轴对称．例如

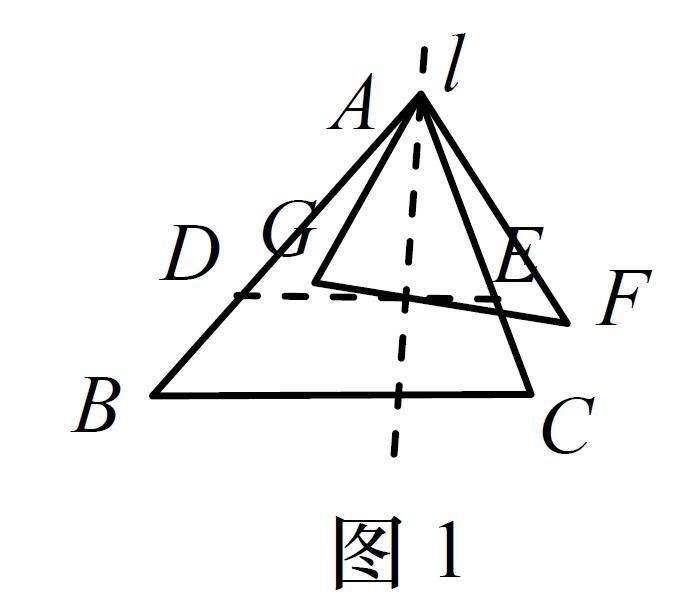
（1）如图1，先将△ABC以点A为位似中心缩小，得到△ADE，再将△ADE沿过点A的直线l翻折，得到△AFG，则△ABC与△AFG成自位似轴对称．

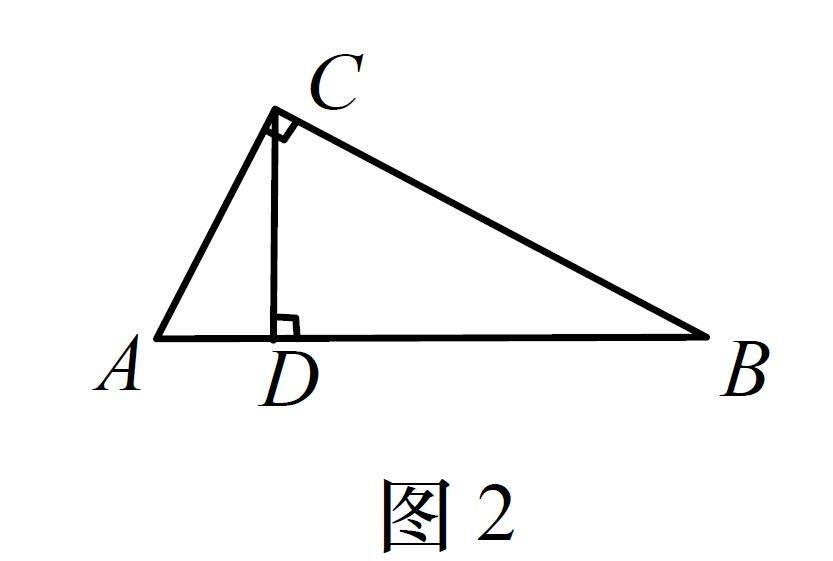
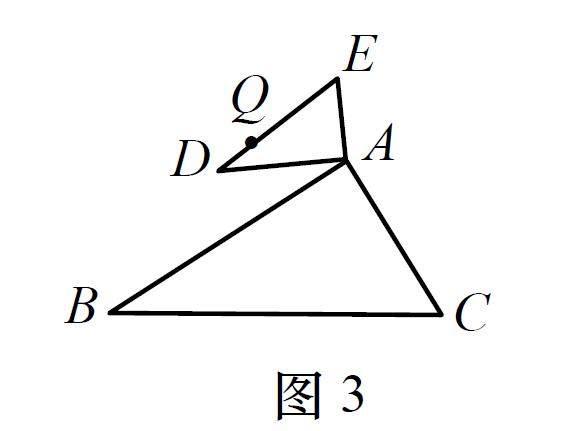
（2）如图2，在△ABC中，∠ACB=90°，AC

（3）如图3，已知△ABC经过自位似轴对称变化得到△ADE，Q是DE上一点，用直尺和圆规作点P，使P和Q是该变化前后的对应点（保留作图痕迹，写出必要文字说明）．

（4）如图4，D为BC中点，∠BAE=∠CAD，∠ABE=∠C，求证DE//AC．

本题是2022年南京中考压轴题，它是一道即学型试题，涉及图形的轴对称、相似变换等知识，考查学生对图形变化的感知、理解和应用，突出对学生空间观念、几何直观、推理能力、模型观念等的考查，对初中阶段的几何教学和核心素养培育起到重要的引领作用．

2 特色解读

2.1 立足教材，凸显知识生长

教材作为数学知识的载体，是课标精神的体现．命题者基于教材中图形变化知识点：位似和翻折，进行了整合与创新，寻找到知识的生长点和延伸点，形成了“即学型”题型．此题综合考查了学生的基本知识和技能的运用能力，数学方法和思想的纵横沟通与联系能力，引导学生体会知识发生，发展和应用的过程，感受知识的整体性，也提醒师生重视模型意识，挖掘其潜在的研究价值．

2.2 注重探究，考查几何直观

本试题是全卷的压轴题，承载着区分和选拔的功能，因此，试题在综合考查“图形与几何”模块的核心基础知识的同时，突出考查了学生的几何直观、逻辑推理等数学思维能力．如本题的第1问，虽然是基础题，但也需要学生具备一定的几何直观和逻辑思维能力，能从新定义的概念中挖掘隐藏的性质．从学生的答题来看，均分不高，也充分暴露了学生在这方面能力的薄弱．

2.3 回归本源，体现数学能力

“解法开放”是此压轴题最后一问的特色．即试题回归到数学本源，注重通性通法．圆内问题“如图5，在圆内接四边形ABCD中，AB=AD，M是BC边的中点，点N在对角线BD上，且满足∠BAN=∠CAM．求证：MN//AC”与此压轴题类似，但是压轴题的图形显然更加简洁大方，并且设置了思维的阶梯，层层递进，同时舍去了圆的大背景，使得学生的思考方向更加的广泛，凸显出本题对于图形变化能力的考查．从学生的做法来看，可谓五彩缤纷，赏心悦目．

3 解法赏析

本题（1）（2）两问比较基础，不做探究．下面主要对于第（3）问，剖析符合学生认知规律的自然解法．

视角1 借助几何直观，利用中位线突破

仔细观察题目中的已知条件“中点D”，结合图形，是否有隐藏的信息？需要证明是过中点D的线段与另外一条线段平行，根据平时几何学习中所积累的解题经验，可以自然的想到通过中位线构造图形并证明．

证法1 如图6，延长BE交AC于点F，由题意易证ΔABE∽ACDΔ，所以AB/AC=BE/CD．

易证ΔABF∽ACBΔ，所以AB/BC=BF/CB，BF/CB=BE/CE，即CD/CB=BE/BF．

因为D为BC中点，所以BE/BF=1/2，即E为BF中点，所以DE为中位线，故DE//AC．

分析 证法1，2自然、简洁，图形的构造相对直接，只需延长BE，就能构造出含有中位线DE的三角形，通过图形相似，找到边的比例关系，最后利用BD=CD转化比例，证出E为BF中点即可．过程中蕴含转化和化归的数学思想，可以体现学生的图形变换能力．证法3是由倍长中线出发，是常用的中点构图方法，但是该证法对学生比例转化的能力要求较高．很多学生倍长中线后，无法继续关联模型，无法构造出含有DE的中位线，导致做法停滞．证法4是同一法的典型案例，难点体现在①：学生不敢去作AB的中点F，而是选择延长DE交于F，后面会因为条件不够而无法说理得证；②：作中点F后，默认DEF，，三点共线，最后导致说理不清．可见此方法对学生的逻辑推理能力要求较高，只有很少学生说理完整清楚，这其实也反映了教师在对于“同一法”的教学中是选择避而不谈的．

视角2 把握问题关联，运用轴对称突破

本题是即学型题型，一般以思维递进形式设计，使用的模型和方法往往一脉相承．所以想一想前面的问题关联，利用轴对称来构造图形，寻找解题的突破口．

分析 本题的立意是位似和翻折整合，形成即学型题目，学生在解决最后一问的过程中需要关联思考前两问的意义和作用，想象图中是否有三角形可以通过位似翻折，继而想到证法5，通过翻折，去思考有没有相似图形出现，如果可以发现新三角形相似，那么推导证明角相等就水到渠成了．在证法5的启发下，证法6自然生成．此方法的难点在于不易察觉到CGBG⊥，学生陷入倒角证明角相等的循环中不可自拔，最后草草收场．证法7是在自相似轴对称的引导下形成A字形相似，再翻折，就会找到ABFΔ≌AGHΔ∽ΔABC，利用比例关系推导出E点为中点，此方法对于构图和识图能力要求较高，学生容易误认为GH过E点，从而做出错误解答．

视角3 借助模型意识，“一线三等角”突破

“同位角或内错角相等，两直线平行”，即“若∠ECB=∠C=∠ABE，则得证”，而这三个角顶点在一条线上，自然联想到“一线三等角”模型，但是这三个角位置还需要调整，如此产生出以下的解题方法，甚是巧妙．

分析 证法8是比较简洁的作法，是思维含量比较高的一种方法，“多思少算”体现得淋漓尽致．此方法要求学生必须对几何证明中的“分析法”了然于心，只有通过分析法推导才能发现隐藏的模型，并且还要通过图形的变化才能真正地形成“一线三等角”模型，突出考查了学生层层突破的能力和分析探究的素养以及寻找问题本源的能力．只有在平时教学过程中真正让学生体会“要证”“即证”“得证”的思维过程，才能让学生真正做到“对症”施策．

4 教学启示

4.1 深挖题目本质，开发优质素材

《义务教育数学课程标准》（2022年版）指出：“广大教育工作者要勤勉认真、行而不辍，不断创新实践，把育人蓝图变为现实．”对经典题目进行创新研究，科学改编开发新颖题目，再作为教学素材探究学习，能够反复地锤炼相关知识，不断地认识问题本质，螺旋式提升思维水平．题目原型图形较为复杂，本题从“简化图形、提升思维、发展素养”的视角去创新，重视基础考查，创设情景引入，改掉大背景，隐掉一些关键的线段，相信读者会惊叹它设计之巧妙．因此，教师在平时备课时，要深挖问题内涵本质，理清整体来龙去脉，不断进行新问题、新思想和新方法的探索，试图开发具有前瞻功能和推广价值的优质教学素材，以精干的研究品质带动学生发扬进取精神，以创新的思维理念引领学生进行创新实践．

4.2 开放课堂探究，助力图形教学

章建跃博士说：“对于‘距离近的知识，如推论、有直接类比对象等知识的教学，教师可以不干预或少干预，让学生独立自学、自主探究．”探究式教学是发展学生思维的重要教学方式，教师出示问题后给足学生时间，鼓励学生自主思考和表达，教师适时点拨而不过多干预．本题的证法1到证法9都是常见的自然解法，若在解题教学课上让学生去逐步展示出来、让小组去深度交流起来，学生的思维就会自然生长．过度灵巧的方法，学生思维难以触及，教师也无需过度展示、强行灌输．小巧一题一法，不应提倡，大巧法无定法，确实太难，出路在于中巧，这里的中巧指的就是有章可循的通性通法．教师在日常教学中，要本着“一切为了发展学生思维”的教学理念，摒弃“满堂灌”的陈旧模式，维持探究教学的良好常态，筑牢思维生长的根本之基，让课堂成为学生思维成长的加油站，使课堂成为学生能力提升的助推器．

4.3 引导关联思考，发展数学能力

数学家G·波利亚在《怎样解题》中指出：“从你获得的那个幸运念头开始，并补充一些可能需要的次要细节，尽可能详细进行你想起的以前可行的所有代数或几何运算．”对问题进行关联思考是破解问题的必由之路，是发展数学关键能力的重要方式．在本题的解答中，学生对“中点”“相似”等条件进行正向思考，对“平行”结论进行逆向思考，想到与之关联的中位线、轴对称、等腰三角形等知识，然后补全其中的证明步骤，搭建起连接条件和结论的桥梁，问题就能迎刃而解，能力也就潜移默化地提升了．即学型题目，关联性还体现在问与问之间，问题一般以思维递进形式设计，使用的模型和方法往往一脉相承，想一想前面的问题间关联，也是寻找突破口的自然思维．因此教师在平时的教学，要让学生去深度关联思考，然后及时进行方法总结，将碎片化的知识整合起来，形成相对完整的知识体系，植根于思维的深处，后续解决此类问题，便可快速调用知识体系中的内容，有条有理地进行思考，科学高效地解决问题．