三峡大坝深孔工作闸门流激振动特性研究

童广勤 张海龙 李奇 伍友富 齐文强

收稿日期：2023-10-20；接受日期：2024-02-01

作者简介：童广勤，男，正高级工程师，主要从事岩土工程、安全监测等工作。E-mail：tong-guangqin@ctg.com.cn

Editorial Office of Yangtze River. This is an open access article under the CC BY-NC-ND 4.0 license.

文章编号：1001-4179（2024） 06-0218-09

引用本文：童广勤，张海龙，李奇，等.三峡大坝深孔工作闸门流激振动特性研究

［J］.人民长江，2024，55（6）：218-226.

摘要：为深入探究三峡大坝深孔弧形工作闸门运行时的流激振动特性，对其进行了原型观测研究。结果表明：在闸门启闭动态运行时，其动位移极值和加速度极值都相对较小，振动较小；在启门、停门瞬间，闸门的动位移极值和加速度极值都明显增大，振动较大；当闸门开度在0.6～0.7时，闸门发生了强迫振动；1号、12号深孔弧形闸门在运行时都不同程度受到了流激振动的影响，但都属于微小或中等振动，处于安全范围内。相关成果可供大坝安全运行管理及闸门设计制造参考。

关  键  词：流激振动； 深孔弧形闸门； 时程分析； 频谱分析； 三峡大坝

中图法分类号： TV663

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2024.06.030

0  引 言

弧形闸门是水利工程中广泛应用的一种闸门型式，常用于水闸和大坝等建筑中，其在运行过程中普遍存在水流作用下引发的流激振动问题［1］。若闸门结构布置不合理或运行不当，流激振动可能会引起闸门过度振动，造成闸门结构部件疲劳失效甚至断裂，影响工程的安全。例如，1995年美国Folsom大坝弧形闸门由于闸门剧烈振动而破坏。因此，研究弧形闸门流激振动特性和相应的减振方法具有重要的理论和实际意义［2］。

目前普遍认为，闸门底部水流的分离和重新附着会导致水流流态不稳定，这种不稳定流态产生的脉动水压力是闸门流激振动的主要激励源［3-5］，不同型式的水动力荷载诱发的闸门振动类型也不同［6］。由于弧形闸门运行时过流条件复杂，目前尚未形成完善的流激振动及抗振设计理论［6-8］。在高坝、大流量、启闭频繁的深孔弧形闸门中，流激振动现象尤为明显，但针对深孔、高坝、大流量弧形闸门振动特性的研究仍显不足。现阶段对闸门流激振动的研究主要采用原型观测、物理模型试验及数值模拟等方法［9-10］，但在现有技术条件下，物理模型、数值模拟方法精度仍不高［11-12］。本文采用原型观测对三峡大坝1号、12号深孔闸门的流激振动特性进行深入研究，获取了闸门的动位移、加速度时程曲线、加速度频谱图及动应力时程曲线等关键动力特性［13］，以期为闸门实际运行及流激振动研究提供参考。

1  深孔工作闸门结构与测点布置

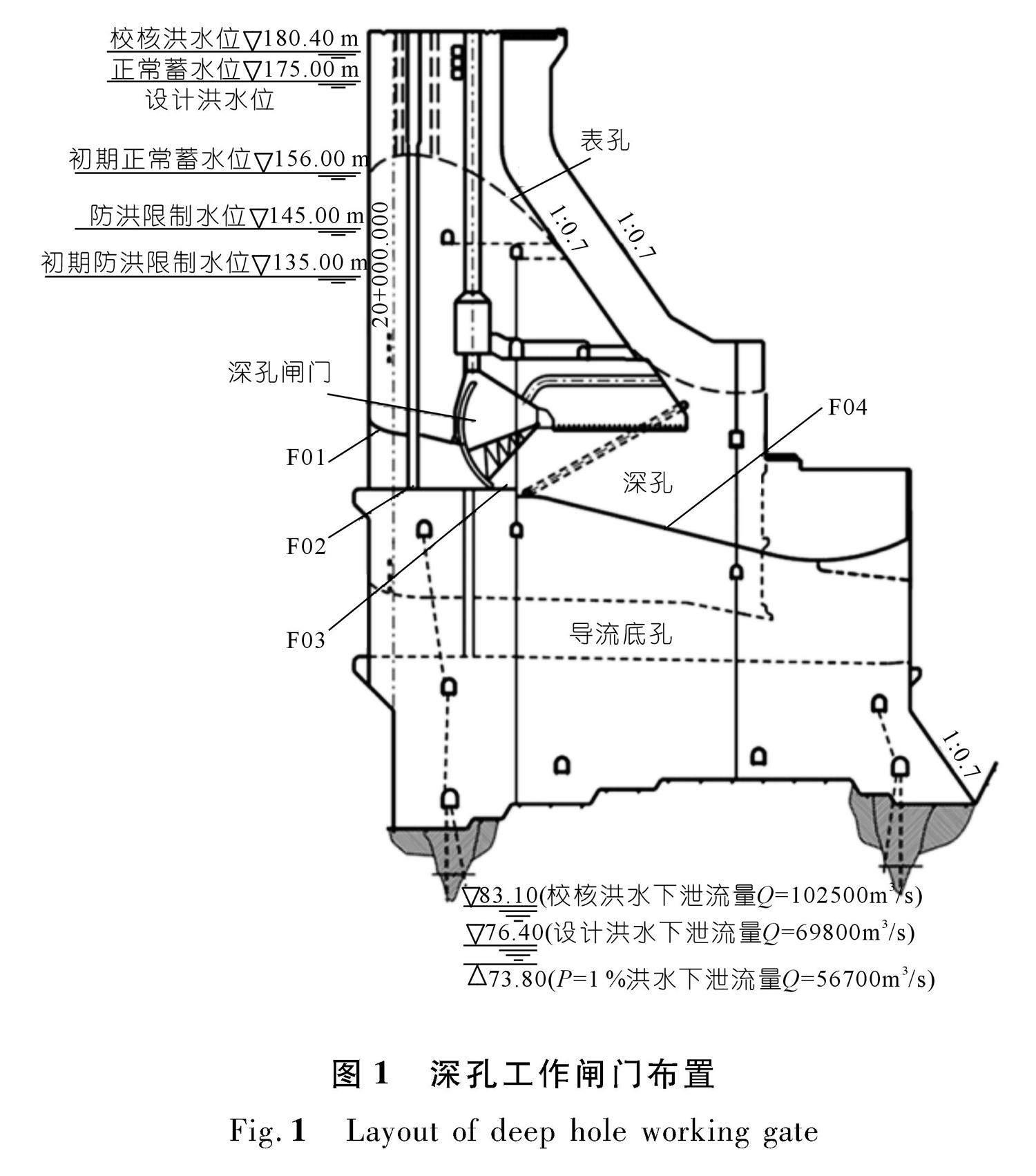
三峡大坝坝身段分为泄洪坝段、厂房坝段和非溢流坝段。泄洪坝段位于河床中部，长约480 m，分为23个坝段，每个坝段布置有1个泄洪深孔，配套一孔弧形工作闸门，深孔工作闸门布置见图1。三峡大坝泄洪深孔具有高坝、泄流量大、流速高、汛期运用时间长、抗冲耐磨要求高等特点［14］。闸门孔口尺寸为7.0 m×9.0 m，底坎高程90.0 m，设计水头85 m，门叶结构为双主纵梁式，面板曲率半径R=16.0 m，采用单吊点4 000/1 000 kN液压启闭机启闭，闸门结构如图2所示。在泄洪深孔内布置有水压力传感器，1号闸门传感器布置如图1所示，测点F01布置在深孔进口侧缘段，F02布置在门槽区域，F03布置在深孔工作门底缘区域，F04布置在深孔跌坎后斜直段。闸门流激振动测试信号共有3类，分别是动位移、加速度和动应力，闸门流激振动信号测点布置如图2所示。图中A测点代表振动加速度测点，共7个，编号A1～A7；Y代表应力测点，共10个，编号Y1～Y10；动位移测点共7个，测点位置与方向与加速度测点相同，编号W1～W7。

对1号、12号深孔工作闸门分别在不同水位条件下的流激振动进行观测，1号工作闸门的测试水位为146.25，150.05，156.50 m，12号工作闸门的测试水位为146.04，149.91，156.12，159.75 m。在各水位下，分别试验闸门开启至全开随后关闭和闸门开启至半开位置随后关闭两个周期的动响应特征。闸门测试一个周期共包含如下阶段：闸门全闭、开门启动、开门运行、停门冲击、全开悬停（半开悬停）、落门冲击、落门运行及闭门冲击。

2  闸门全开过程脉动压力测试

F01和F03测点在启门过程时的压力变化曲线如图3所示。在1号闸门全开过程中，F01、F02测点压力随闸门开度增加而降低，压力脉动幅度较小；在闸门开启过程中，F03测点压力逐渐升高，脉动压力幅度较大。F04测点在闸门开启初期，出现一段时间的负压，随着闸门开度的逐渐加大，压力升高。

分析可知，在闸门开启过程中，脉动压力幅度变大，流态不稳定，闸门底缘受到水流脉动压力影响，闸门受到了流激振动作用的影响。

3  振动加速度及动位移时程

在146.25 m水位条件下，1号工作闸门全开周期过程中，闸门右下支臂侧向的动位移和加速度时程曲线如图4所示。由图可知，闸门动位移与加速度在启闭过程的变化规律相似。在启门、停门、落门和闭门瞬间，动位移与加速度曲线均出现峰值，表明此时闸门上出现冲击，振动幅度最大；在启门至全开过程中，当开度在0.6～0.7时，A3测点的加速度和动位移曲线出现峰值，测试结果与深孔弧形闸门水弹性模型试验结果一致，表明闸门在此工况下出现了强迫振动，应避免闸门长时间在此开度下运行［15-16］。在闸门开启过程中，随着开度的增加，闸门上的振动逐渐增大。在全开及半开周期的悬停状态下，振动平稳，幅度较小。在闸门落门运行过程中，随着开度减小，振动逐渐减小，振动规律与启门状态相反。在其他各测试水位下，1号和12号工作闸门在开启泄洪过程中闸门上的动位移和加速度变化均表现出相同规律。

表1为1号工作闸门在150.05 m水位下全开和半开周期中，各测点的动位移极值情况。图5和图6分别为1号和12号工作闸门在146.25 m和146.04 m水位下，全开和半开周期中各测点动位移极值变化。在所有测试水位的全开和半开周期中，1号闸门动位移最大值均发生在测点W3的落门启动冲击时刻，在水位150.05 m时，闸门全开过程中动位移极值最大达到0.260 mm。1号工作闸门在各个测试水位的全开悬停阶段和半开悬停阶段，最大动位移为0.006 mm和0.033 mm。12号闸门在全开周期中，测点W5的动位移在各测试水位下的落门启动冲击时刻均最大；而在半开周期中，测点W3的动位移在各水位下的落门启动冲击时刻均最大。在水位156.12 m时，全开周期的落门启动冲击时刻W5测点的动位移值最大为0.220 mm。12号闸门在全开悬停和半开悬停阶段的最大动位移分别为0.010 mm和0.020 mm。

表2为1号工作闸门在150.05 m水位下全开和半开周期各测点上加速度极值。图7和图8分别为1号和12号工作闸门在146.25 m和146.04 m水位下全开和半开周期各测点的加速度极值变化图。在各测试水位的全开和半开周期中，1号闸门加速度的最大值均出现在启闭过程中。在此阶段，加速度的最大值为0.83 m/s2，此时的闸门受到了冲击。在全开悬停阶段和半开悬停阶段，加速度的值相对较小，分别为0.08 m/s2和0.31 m/s2。12号工作闸门在各测试水位下的全开和半开周期中，加速度变化规律与1号闸门相同。启闭过程中的振动加速度最大值为1.40 m/s2。在全开悬停阶段和半开悬停阶段，12号工作闸门的最大加速度分别为0.48 m/s2和0.66 m/s2。

结合动位移和加速度时程曲线以及水压力变化曲线的分析可知：（1） 弧形闸门闭门挡水、全开及半开悬停均是平稳过程，启门和闭门过程则属于非平稳过程。在平稳过程中，由于闸门的出流流态相对稳定，水流脉动压力幅度较小，闸门的振动较小；在非平稳过程，闸门的出流流态变化明显，水流脉动压力幅度较大，闸门的振动较为显著。

（2） 在全开周期过程中，闸门过流流量更大，流速更快，因而闸门在全开周期中的动位移和加速度极值比在半开周期中更大，振动更为明显。闸门初始状态相同，因而全闭和开门启动冲击时刻，全开周期与半开周期动位移极值和加速度极值相差不大，与实际过程相符。在悬停过程中，全开周期的振动没有半开周期明显。这是因为在悬停过程中，闸门的过流流态趋于稳定，而半开状态工作闸门与下泄的水接触，全开状态闸门完全与下泄水脱离。

（3） 工作闸门最大动位移均出现在下主梁或下支臂上，这是因为下主梁和下支臂是关键的受力结构，且布置于闸门下半部分，受下泄水流作用明显。验证了文献采用混沌理论对闸门振动进行分析的结果：即下主梁相较于其他位置，振动更加明显。

（4） 闸门侧止水与侧墙埋件相接触，对闸门产生侧向位移约束，因而闸门动位移极值均表现为切向方向。

（5） 在全开和半开周期，1号和12号工作闸门动位移大小为同一个量级，振动差异并不显著。根据美国 Arkansas河闸门振动危害程度位移判别标准，闸门位移均方根在0～0.050 8 mm之间的振动可忽略不计，在0.050 8～0.254 mm之间的振动为微小振动，在0.253～0.508 mm之间的振动为中等振动［17-18］。因而1号和12号闸门的振动均属于微小振动或中等振动，处于安全允许范围内。

4  动位移及加速度频谱

图9～12展示了不同水位下，工作闸门右下支臂侧向测点在全开和半开周期的动位移和加速度时频图，时频图上的脊线代表了频谱的峰值［19］。12号工作闸门右下支臂侧向测点W4的动位移和A4加速度振动信号在全开和半开过程的时频变化规律与1号工作闸门相同。观察可知：（1） 测点振动信号频率内容丰富，闸门在闭门挡水和悬停阶段，其振动信号的频率结构相对稳定；在启门和闭门过程，闸门上的振动信号的频率结构产生变化，这是因为在非平稳过程中水流脉动压力幅值和频率处于不稳定状态，变化较大，水流流激振动作用导致闸门的振动频率发生变化。

（2） 1号工作闸门W4测点的振动位移信号中有几条随开度变化而变化的脊线，这与先前研究结论吻合：随着闸门的开度的改变，水流耦合作用会影响闸门结构的频率［20］。当闸门接近全开状态时，这些脊线变化速度加快，而有限元结果显示：当闸门接近全开状态时，闸门的模态频率发生快速变化，两者结果一致。这是因为闸门接近全开状态时下泄水流与闸门脱离，闸门不受下泄水流扰动的影响，此时闸门刚度最小，完全脱离水体，没有脉动水压力作用，因此其振动相对较小。

（3） 半开周期时频图则显示，测点W4上的振动信号频率结构的变化相对较小，这是由于水流耦合作用对闸门约束较强，因而在半开悬停过程中，闸门振动并不显著。

5  动应力测试

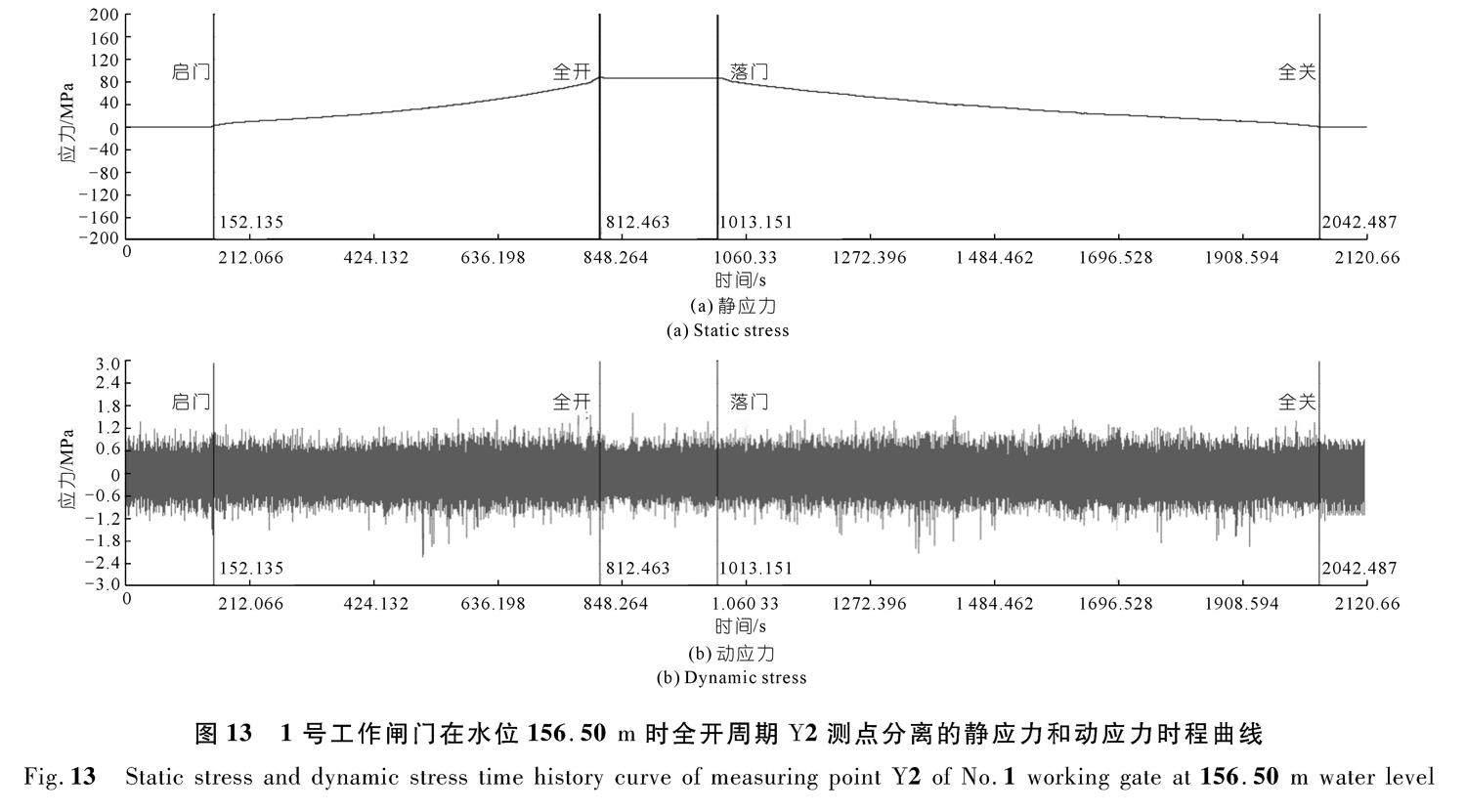
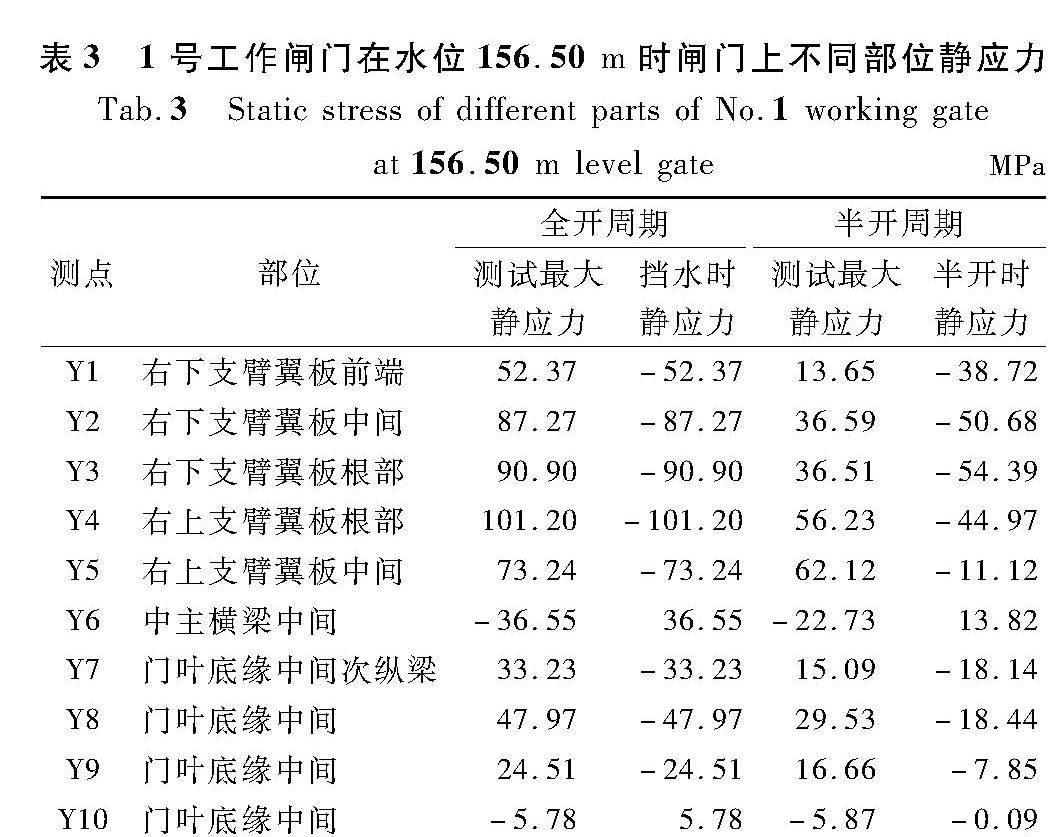
经试验测得的应力为相对值，可应用动/静应力分离处理方式得到闸门上的真实应力。分离的动应力信号为闸门振动过程中产生的应力波动值，静应力信号反映了闸门状态和荷载发生变化后闸门上的应力变化情况。通过分离出来的静应力信号可换算出闸门上实际静应力，再与分离出的动应力合成，进而得到闸门上的真实应力状态。经分离，得到156.50 m水位时1号工作闸门Y2测点的静、动应力时程曲线如图13所示，闸门上不同部位的应力状态如表3所示。

动应力均方根值是衡量闸门振动强弱的重要指标。通过对分离得到的动应力信号进行分析，可以得到不同测试水位下各测点的动应力均方根值，表4为1号工作闸门在156.50 m水位时的动应力均方根值。表5列出了根据3σ原则确定的各运行阶段下闸门支臂的振动动应力最大值。分析可知：（1） 在半开周期状态下，各测点的应力值均低于闭门状态。同时，随着开度的增加，闸门上的应力呈现下降趋势，但应力值与开度并非呈线性关系。在半开状态下，闸门上的应力约为闭门状态的3.73%～73.20%，即应力减小了96.27%～26.80%。

（2） 在相同水位条件下，闸门在各运行阶段的动应力均方根差异并不显著，这意味着在整个运行状态下，闸门的振动强度相对稳定。与闸门结构静应力相比，流激振动引起的闸门动荷载较小，闸门有较大的强度储备，能够确保其安全运行。

（3） 在闭门阶段，闸门上的振动动应力达到最大值，但支臂上的动应力值相对较小。将动应力与静应力进行叠加后，闸门支臂仍然具有较大的强度储备。因此，对于1号和12号工作闸门，由于流激振动引起的结构应力变化相对较小，它们仍处于安全状态。

6  结 论

（1） 闸门在启闭过程中，动位移与加速度时程曲线变化规律一致。当闸门开启时，随着开度的增加，闸门的振动逐渐增强，而在落门过程中，振动规律与启门过程相反。在启门、停门、落门和闭门这些瞬间，闸门上出现冲击，振动幅度最大。在启门至全开过程中，当开度在0.6～0.7范围内时，闸门出现了强迫振动，应避免闸门长时间在此开度下运行。

（2） 闸门在闭门挡水、全开及半开悬停阶段状态为平稳过程，而在启门和闭门阶段，其状态为非平稳过程。在平稳过程中，水流脉动压力幅度较小，闸门的振动相对较小。而在非平稳过程，水流脉动压力幅度较大，闸门的振动较大。闸门在全开周期中的振动比在半开周期中更为明显。

（3） 闸门的最大动位移均出现在下主梁和下支臂上。闸门侧止水与侧墙埋件相接触，对闸门产生侧向位移约束，因而闸门动位移极值均表现为切向方向。

（4） 对于1号闸门和12号闸门，其在各个方向的振动均属于微小振动或中等振动，可认为是安全的。

（5） 在闭门挡水和悬停阶段，闸门振动信号的频率结构相对稳定；而在启门和闭门过程中，闸门振动信号的频率结构发生变化。

（6） 随着开度的增加，闸门上的应力呈现下降趋势，但应力值与开度并非呈线性关系。1号、12号深孔工作闸门在运行时，由于流激振动引起的动应力变化相对较小，闸门结构仍有较大的强度储备，闸门运行时处于安全状态。

参考文献：［1］  刘昉，李文胜，王延召，等.巴塘水电站导流洞平面闸门流激振动试验研究［J］.水资源与水工程学报，2021，32（1）：136-142.

［2］  刘计良，奚宏林，司政，等.基于流固耦合的弧形闸门-闸墩体系的流激振动研究［J］.水资源与水工程学报，2023，34（5）：149-154，171.

［3］  LEE O S，SEONG H，KANG W J.Flow-induced vibration of a radial gate at various opening heights［J］.Engineering Applications of Computational Fluid Mechanics，2018，12（1）：91-100.

［4］  KOLKMAN P A.Flow-induced gate vibrations：prevention of sef-excitation computation of dynamic gate behaviour and the use of models［M］.Delfe：Judels，1976.

［5］  SHEN C，WANG W，HE S，et al.Numerical and experimental comparative study on the flow-induced vibration of a plane gate［J］.Water，2018，10（11）：32-39.

［6］  严根华.水工闸门流激振动研究进展［J］.水利水运工程学报，2006（1）：66-73.

［7］  王正中，张雪才，刘计良.大型水工钢闸门的研究进展及发展趋势［J］.水力发电学报，2017，36（10）：1-18.

［8］  张维杰，严根华，陈发展，等.深孔弧形闸门静动力特性及流激振动［J］.水利水运工程学报，2016（2）：111-119.

［9］  朱俊杰，刘圣凡，董玉增，等.调水工程弧形闸门振动测试分析及除振措施［J］.中国农村水利水电，2023（11）：224-228.

［10］马斌，郭乙良.水工闸门振动研究现状及发展趋势［J］.水利水运工程学报，2019（2）：55-64.

［11］彭思贤，赵兰浩，毛佳.大宽高比弧形钢闸门流激振动数值分析［J］.水利水电科技进展，2022，42（3）：90-96.

［12］蒲楠楠，柯亚唯.原型观测试验在泄洪闸门振动特性分析中的应用［J］.水利与建筑工程学报，2022，20（3）：46-52.

［13］YAN H G，CHEN Z F，DONG J.Study of flow-induced vibration for the high-head and large dimension gate［J］.Applied Mechanics and Materials，2012，18，170-173.

［14］王小毛，徐麟祥，廖仁强.三峡工程大坝设计［J］.中国工程科学，2011，13（7）：70-77.

［15］张林让，张晓平.三峡大坝深孔弧形闸门流激振动水弹性模型试验研究［C］∥中国力学学会论文集，北京，2001.

［16］LU Y，LIU Y，ZHANG D，et al.Chaotic characteristic analysis of spillway radial gate vibration under discharge excitation［J］.Applied Sciences，2023，14（1）：31-42.

［17］徐爽.深孔式弧形工作闸门流激振动危害评价及防振［J］.东北水利水电，2022，40（1）：66-67.

［18］王文涛，石清文.枕头坝一级水电站泄洪闸弧形闸门流激振动研究［J］.人民长江，2021，52（增2）：216-219.

［19］DING P，YUE G，YU P，et al.Vibration response testing and evaluation of a hydropower stations gate［J］.Journal of Physics：Conference Series，2021（1）：102-126.

［20］尤亚攀.基于流固耦合的南水北调工程闸门结构性能及动力特性研究［D］.郑州：华北水利水电大学，2022.

（编辑：胡旭东）

Study on fluid-induced vibration characteristics of deep-hole gate of Three Gorges Dam

TONG Guangqin1，2，ZHANG Hailong1，2，LI Qi3，WU Youfu3，QI Wenqiang3

（1.Hubei Key Laboratory of Operation Safety of High Dam and Large Reservoir，Yichang 443100，China;

2.River Basin Complex Administration Center，China Three Gorges Corporation，Yichang 443100，China;

3.Changjiang Survey，Planning，Design and Research Co.，Ltd.，Wuhan 430010，China）

Abstract：

In order to deeply explore the flow-induced vibration characteristics on the deep-hole radial working gate of the Three Gorges Dam during operation，prototype observation study was carried out.The time-history analysis and spectrum analysis results showed that when the gate was opened and closed dynamically，the extreme values of vibration dynamic displacement and acceleration were relatively small，and the vibration was small.At the moment of opening and stopping，the dynamic displacement extreme value and acceleration extreme value of the gate increased obviously，and the vibration was large.When the gate opening was 0.6～0.7，the forced vibration of the gate occurred.The No.1 and No.12 deep hole radial gates were affected by flow-induced vibration to varying degrees during operation，which was small or medium vibration in the safe range.The relevant results can be used as reference by dam safety operation personnels.

Key words：

flow-induced vibration; deep-hole radial working gate; time-history analysis; spectrum analysis; Three Gorges Dam