长江口徐六泾站垂线含沙量代表层研究

姜璇 闻卫东 支远哲 刘传杰 邵宇阳

收稿日期：2023-12-05；接受日期：2024-02-01

基金项目：国家自然科学基金联合基金重点项目（U2040203）；上海市水务局科研项目（沪水科2020-02）

作者简介：姜  璇，女，硕士研究生，主要从事河口海岸泥沙动力学方面研究。E-mail：1215613386@qq.com

通信作者：邵宇阳，男，副教授，博士，主要从事河口海岸泥沙动力学方面研究。E-mail：syy@hhu.edu.cn

Editorial Office of Yangtze River. This is an open access article under the CC BY-NC-ND 4.0 license.

文章编号：1001-4179（2024） 06-0106-08

引用本文：姜璇，闻卫东，支远哲，等.

长江口徐六泾站垂线含沙量代表层研究

［J］.人民长江，2024，55（6）：106-113.

摘要：在水深大、交通繁忙而无法开展传统六层采样测量的情况下，如何获取更为准确的垂线平均含沙量进而提升入海泥沙通量的测量精度是当前学者关注的重点。以长江口入海观测关键节点——徐六泾水文断面为例，采用多种分层组合的方法计算垂线平均含沙量，运用置信区间、平均相对误差以及Lilliefors假设检验等统计方法进行计算与分析；同时，结合观测节点上下游水文断面数据，分析了垂线平均含沙量代表层的表征规律。研究结果表明：虽然徐六泾水文断面受到径-潮流相互作用，但0.6H层被证实是最佳的垂线平均含沙量代表层，其平均相对误差均值在（0±5）%范围内；然而在下游南支河段，白茆沙水文断面受潮汐动力的影响显著增大，从而导致0.6H单层代表性较差。研究成果对未来水文综合浮标改造和准确获取长江入海泥沙通量具有重要指导意义。

关  键  词：含沙量； 代表层； Lilliefors假设检验； 误差分析； 徐六泾水文断面； 长江口

中图法分类号： TV148+.1

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2024.06.015

0  引 言

长江口为中等强度的潮汐河口，在径流、潮流、波浪、盐水楔以及增减水等多种变化的动力因素作用下，河口的泥沙运动规律及其分布较为复杂［1］。徐六泾水文断面作为长江口的重要入海节点，其水沙运动受径流为主的径潮流双向运动影响，并且其水沙通量能很好地体现进入长江口门区域的沙源量和淡水资源的丰沛程度。这不仅影响着长江口滩槽演变，而且对长江口航道冲淤与河势变化的分析，以及长江口的保护与治理具有现实价值和科学意义［2］。目前在徐六泾水文站一般利用光学后散射仪（OBS-3A）的单点测沙结果对声学多普勒流速剖面仪（ADCP）的声散射强度进行标定，以获取垂线平均含沙量。然而，由于现有条件下水文综合浮标中光学测沙仪的测量位置接近水面以下4 m处，且ADCP的顶部和底部存在测量盲区，因此目前的测量结果存在较大误差［3］。并且考虑到该区域水深大、交通繁忙，传统采样也难以实施。因此，为了提高入海泥沙通量的测量精度，本文拟采用代表层方法来表征徐六泾河段的垂线平均含沙量。

在恒定流领域，代表层方法已经得到了广泛应用，如目前长江大通水文站已经全面使用0.6H层作为该站点的代表层，以表征垂线平均含沙量［4-5］。然而，徐六泾属于径潮流站，其含沙量的分布特性相较于大通站等单纯的径流站点更为复杂。尽管在非恒定流领域，代表层方法的研究尚处于探索阶段，但也已取得了一些相关研究成果：Xie等［6］提出了使用三点法来测量计算悬移质泥沙浓度，以探索潮汐对悬移质沉积物浓度的影响；Box等［7］通过三点法与单点法相结合，测定了河口浅滩区域的垂线平均含沙量；在研究潮汐对河口盐度的影响时，Gao等［8］采用了三点法代替六点法测量含沙量；而Yang等［9-10］在模拟非恒定流的水槽试验中，运用光学后向散射技术发现，0.6H层可以作为代表层表征垂向含沙量；Quan等［11］研究潮汐河口垂直流速分布对含沙量计算的影响时发现，0.6H层的测量数据与计算所得的含沙量数据更贴近。综合以上研究，已经有先例证明受径潮流作用的河口海岸地区也可以通过计算某层或多层的平均含沙量来作为代表层表征垂线平均含沙量。然而，在长江口徐六泾河段尚未进行针对性研究。因此，本文结合现有徐六泾站多年实测水样数据，采用多种分层组合的方法计算垂线平均含沙量，并通过置信区间、平均相对误差以及Lilliefors假设检验等分析方法，旨在找到并证明适用于该河段的代表层，为未来改进水文综合浮标和获取水文资料提供支撑。

1  研究对象和方法

1.1  研究区域概况

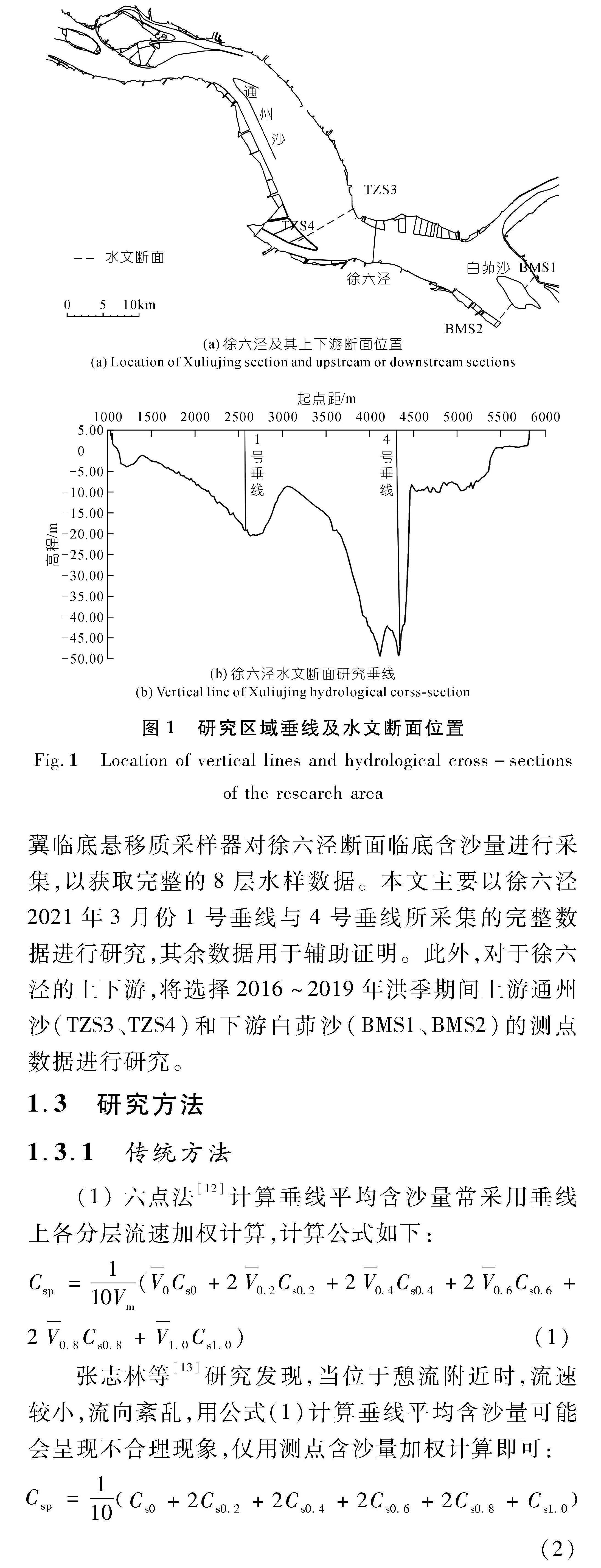
徐六泾断面位于长江口徐六泾节点段，所在河段上承通州沙（TZS）汊道段，下连白茆沙（BMS）汊道段［12］，3个断面位置图如图1（a）所示。徐六泾断面呈不对称“W”形，主深槽宽约2.35 km，最深点达-48 m［13］。近年来，徐六泾断面右岸新通海沙岸线综合整治工程以及左岸常熟边滩整治工程的实施使得边滩处形成次深槽（深度约-15 m），并加深了主深槽的最深点位置，如图1（b）所示。本文选择次深槽（1号垂线）和主深槽（4号垂线）作为主要研究垂线，并开展针对性地垂线含沙量分层现场观测，采集相关水沙数据。

1.2  研究数据

徐六泾现有水沙数据包括2003年和2004年大、中、小潮时1号、2号、3号、4号、5号垂线，2019年6月大、中、小潮时1号垂线，2019年12月大、小潮时1号和4号垂线，2021年3月大、中、小潮时1号和4号垂线。2003年和2004年的数据使用横式采水器按六点法进行采样，采样频率为1次/h。共记录了6层水样数据：表层、0.2H、0.4H、0.6H、0.8H和底层（H为水深，表层指水下0.5 m，底层指距底床高度0.7 m）。由于贺莉等［14］研究发现，悬移质泥沙的垂线浓度分布呈现近底泥沙浓度突增的新现象。于是，在2019、2021年的数据采集中，采用了刘传杰等［12］提出的新型双尾翼临底悬移质采样器对徐六泾断面临底含沙量进行采集，以获取完整的8层水样数据。本文主要以徐六泾2021年3月份1号垂线与4号垂线所采集的完整数据进行研究，其余数据用于辅助证明。此外，对于徐六泾的上下游，将选择2016～2019年洪季期间上游通州沙（TZS3、TZS4）和下游白茆沙（BMS1、BMS2）的测点数据进行研究。

1.3  研究方法

1.3.1  传统方法

（1） 六点法［12］计算垂线平均含沙量常采用垂线上各分层流速加权计算，计算公式如下：Csp=110Vm（V0Cs0+2V0.2Cs0.2+2V0.4Cs0.4+

2V0.6Cs0.6+

2V0.8Cs0.8+V1.0Cs1.0）（1）

张志林等［13］研究发现，当位于憩流附近时，流速较小，流向紊乱，用公式（1）计算垂线平均含沙量可能会呈现不合理现象，仅用测点含沙量加权计算即可：Csp=110Cs0+2Cs0.2+2Cs0.4+2Cs0.6+2Cs0.8+Cs1.0（2）

（2） 三点法通常采用垂线上0.2H、0.6H和0.8H进行计算，公式如下：Csp=V0.2Cs0.2++V0.6Cs0.6+V0.8Cs0.8V0.2+V0.6+V0.8（3）

（3） 单点法通常采用垂线上某一点，如0.6H层含沙量结合ADCP获取的平均流速进行计算，公式如下：Csp=Cs0.6（4）

上述式中：Csp表示垂线平均含沙量，kg/m3；Csj表示测点含沙量，kg/m3；Vi表表示的是测点平均流速，m/s；Vm表示垂线平均流速，m/s。

1.3.2  置信区间

对于小样本（n≤30），置信水平为1-α的置信区间为

k=x±t0×s/n（5）

式中：t0是t分布的临界值，x是样本均值，s是样本标准差，n是样本容量。

1.3.3  假设检验

假设检验的目的在于判断原假设的总体和实际总体是否发生了显著差异。其中，双样本t检验是一种参数化检验，检验统计量的计算公式为

t=x－ys2xn+s2ym（6）

在假设两个数据样本来自具有方差齐性的总体情况下，原假设的检验统计量具有自由度为n+m-2的学生t分布，样本标准差为

s=n－1s2x+m－1s2yn+m－2（7）

此时，检验统计量的计算公式为

t=x－ys·1n+1m（8）

式中：x 和y是样本均值；sx和sy是样本标准差；n和m是样本大小。

1.3.4  误差统计

相对误差计算公式：X′=Csi－CiCi×100%（9）

标准差计算公式：se=1n－2ni=1Csi－CiCi2（10）

式中：se为标准差；X′为相对误差，%；Csi为第i次常规法测得的垂线平均含沙量，kg/m3；Ci为第i次六点法计算的垂线平均含沙量，kg/m3；n为样本大小。

2  垂线平均含沙量

2.1  相关性分析

相关性分析可以用来评估垂线平均含沙量与各层含沙量之间的线性关系强度，并提供量化的指标。相关系数的取值范围为-1～1之间，皮尔逊相关系数计算公式如下：r=ni=1xi－xyi－yni=1xi－x2ni=1yi－y2（11）

式中：r为皮尔逊相关系数；xi，yi分别为第i次采用单点法和六点法获得的含沙量，kg/m3；x，y分别为其对应含沙量均值，kg/m3。

从表1中可以看出，2021年的垂线平均含沙量与各层含沙量之间存在着良好的相关性，特别与0.4H层和0.6H层相关系数的均值均超过了0.9。

2.2  垂线含沙量变化

相关性分析可以帮助比较不同代表层的平均含沙量与垂线平均含沙量之间的线性关系强度。然而，在选择代表层时，需要综合运用其他方法进行判断，以确定它们之间的具体数量关系。图2展示了2021年3月份1号与4号垂线在不同潮型下的垂线含沙量变化以及平均含沙量的波动范围。

从图2中观察到，徐六泾断面1号垂线与4号垂线在不同潮型下的含沙量垂向变化为：1号垂线各潮型的含沙量大于所对应4号垂线的含沙量，垂向含沙量从表层至底层逐渐增大，此规律与黄李冰等［15］的研究结果一致。在1号垂线处，从表层至0.6H层的含沙量较低且随深度变化较小。从0.6H层开始，含沙量明显增加，越靠近底层含沙量越高。在4号垂线处，由于水深较深，水流对泥沙的扰动作用较弱，整个断面的含沙量分布相对均匀。观察1号与4号垂线的垂向含沙量变化，可以对代表层进行初步预测，经计算得各潮型对应的垂线平均含沙量均位于0.4H～0.8H层之间，且大部分集中在0.6H层处。

3  测沙精度分析方法

刘传杰等［12］通过增加近底两层含沙量值进行八点法计算，总结出：计入近底悬沙后，1号垂线处的平均含沙量平均增幅仅为7.37 %，而4号垂线处的增幅小于1 %。考虑到该增幅在接受范围以内，并且六点法作为垂线平均含沙量已具有足够可靠性［16］，故本文将以六点法计算所得的垂线平均含沙量作为被认可的“真值”，并且采用单点法和三点法计算得到的平均含沙量与该“真值”进行比较和分析，找到最能够表征真值结果的方法。

3.1  置信区间分析

置信区间是由样本统计量所构造的总体参数的估计区间，展示的是数据的可信程度，落入置信区间以内的数据被认为可信，反之则不可信。为了将流速纳入考虑范围内，图3主要展示了0.4H、0.6H、0.8H 3个代表层以及三点法和六点法计算所得的单宽输沙率。单宽输沙率的计算公式为：单宽输沙率=垂线平均含沙量×平均流速。

如图3所示，在95%置信区间的条件下，0.6H层数据点基本上均匀地分布在置信区间内，仅有少数分布在区间之外，数据集中程度较高。与0.6H层的数据相比，0.4H层和0.8H层的数据分布相对不均匀，这两层数据与真值数据的离散程度较大，数据的集中程度较低。图3证明了选用0.6H层作为代表层具有较高的可信度，为了进一步分析0.6H层是否达到精度要求，下文将使用相对误差与假设检验等数学方法进行验证。

3.2  相对误差分析

Lu等［17］对各种测量技术所得的相对误差进行综合比较，最终选择相对误差较低的方法进行后续统计分析。本文借鉴其思想，绘制了不同垂线以及不同计算方法下的相对误差，如图4所示。

由图4可知，三点法的测量误差最小，可以最精确地表征垂线平均含沙量，其次0.6H层单点法的相对误差也较小，因此在徐六泾河段可以采用0.2H、0.6H和0.8H层单点法组成的三点法来替代六点法，从而缩短采样时间。在合理误差范围内，甚至可采用0.6H层的数据代替传统六点法计算结果，以提高测量效率。

3.3  假设检验分析

本文将使用双样本t检验和秩和检验来验证在徐六泾河段使用0.6H层单点法、三点法、六点法计算的含沙量数据之间是否具有可替代性，分别对检验的两组数据进行平均值和中位数差异分析。若假设检验结果二者都可以接受原假设H0，则证明假设成立。Razali等［18］在比较双样本t检验中的几种假设检验统计量时曾阐述到，Kolmogorov-Smirnov（KS）统计量属于EDF统计量的上确界类，这类统计量基于假设分布和经验分布之间的最大垂直差异。给定n个有序数据点x1＜x2＜…＜xn，科诺菲尔将Kolmogorov提出的检验统计量定义为

T=supxFx－Fnx（12）

式中：sup代表上确界；F*（x）是假设的分布函数；Fn（x）是基于随机样本估计的EDF。在KS正态性检验中，F*（x）被认为是具有已知均值μ和标准差σ的正态分布。

Lilliefors（LF）检验是KS检验的改进。KS检验适用于假设分布参数完全已知的情况。然而，在分布未知时很难初始地或完全地指定参数。例如在本文中就无法使用KS检验判断一组含沙量数据的直观分布：对于一组超过25个样本的含沙量数据，在没有给定其样本均值与标准差的情况下无法使用该检验法。此时，需要基于样本数据来估计参数，所以如果使用原始KS统计量，结果可能具有误导性，I型错误（弃真）的概率往往较大。所以，与KS检验相比，LF检验的参数估计基于样本，并且可以减小由于“弃真”而出现假设检验判断失误的情况，大大提高了这3组含沙量数据（0.6H层单点法、三点法、六点法）进行假设检验得到的结果精度。因此，在这种情况下，LF检验将优于KS检验。给定一个观测样本，LF统计量定义为

D=maxxFX－SnX（13）

式中：max代表最大值；Sn（X）是样本累积分布函数；F*（X）是累积正态分布函数。并且样本均值为μ=x，样本方差为s2，定义其自由度（分母）为n-1。

考虑到实施双样本t检验的前提是两个样本数据符合正态分布假设和方差齐性假设，本文采用了LF检验，包括了样本均值和标准差的估计［19-20］，检验结果如表2所列。

由表2可知，只有2003年枯水期有一个测次出现拒绝原假设的情况。图5为2003年枯水期的假设检验数据图，观察到出现拒绝原假设是在中潮时1号垂线处，结合其余年份枯水期的假设检验结果分析，可能是存在数据的测量误差，该测点不能作为评估代表性的关键点。

4  分析与讨论

4.1  徐六泾断面平均相对误差分析

本节将对两个不同断面位置、3种不同潮情以及两个不同潮流状态下的数据进行处理分析，确认所选的0.6H层为最佳代表层。即将三点法数据、单点法数据与真值数据进行平均相对误差分析计算，表3为计算结果。

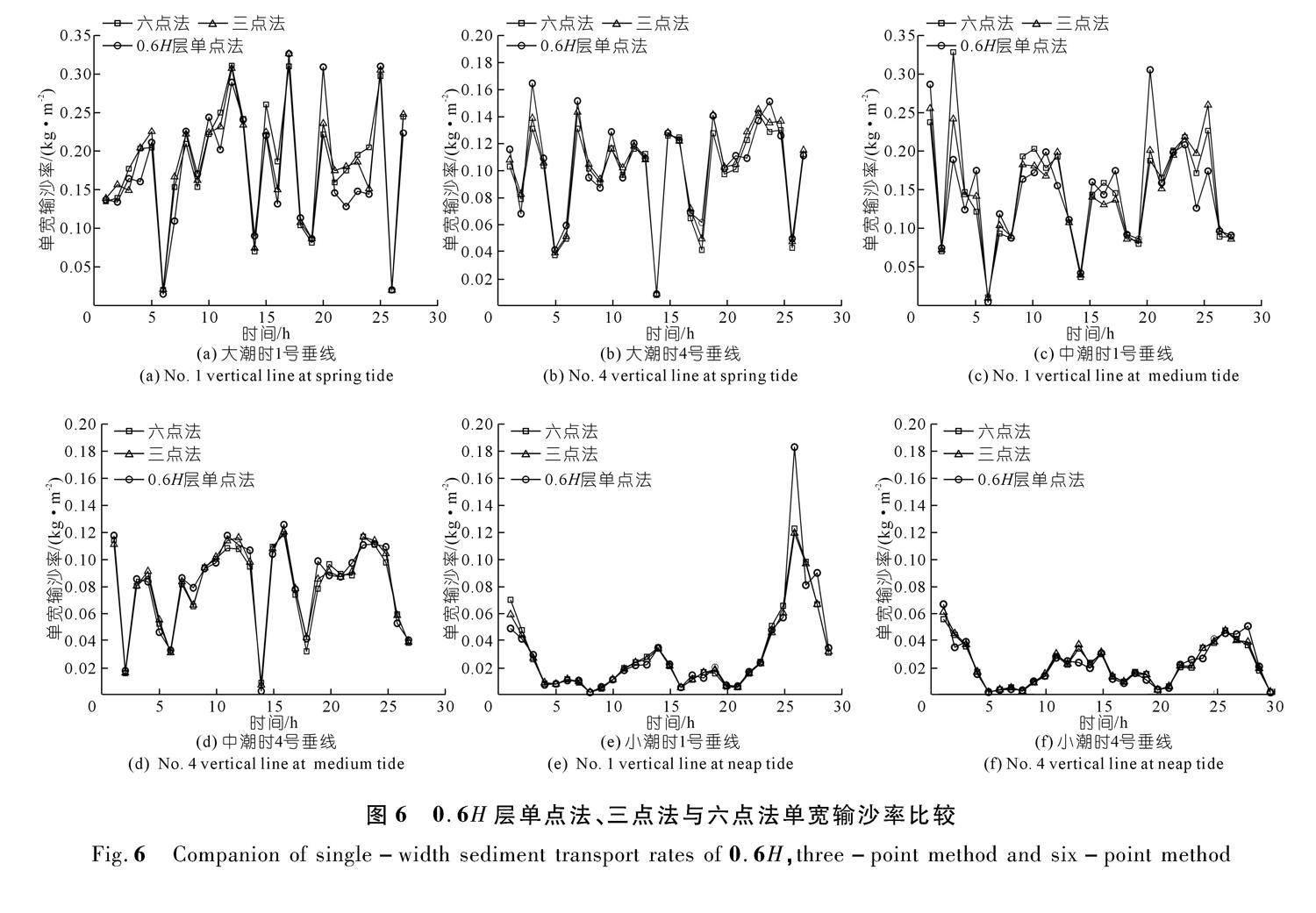
由表3可知：在徐六泾河段，位于次深槽1号垂线处的水流扰动较大且不稳定，平均相对误差普遍较高；而在主深槽4号垂线处，水流相对规则和稳定，平均相对误差较低。平均相对误差的结果表明：三点法结果整体上优于单点法；在单点法中，0.6H层的相对误差较低，误差范围在（0±5）%以内，具有一定的稳定性；并且，在某些情况下0.6H层的精度甚至优于三点法，证实了在徐六泾河段，0.6H层数据具有显著代表性。图6展示了2021年3月的0.6H层单点法、三点法与六点法单宽输沙率比较图，阐释了这3种计算方法的整体差异与具体差异。可以看出，3种方法在大潮时结果差异略大，小潮时差异略小，1号垂线处差异大于4号垂线处。小潮优于大潮是因为在大潮时，潮水水流湍急，潮汐引起的海流会进一步影响河流水位和流速，导致各方法输沙率产生差异，而小潮时受海流影响较小，水流相对稳定且缓慢［21］。4号垂线的差异小于1号垂线是因为主深槽水流速度相对较快且水流通常更加均匀，流速分布较为一致，所以各方法输沙率差异较小；而次深槽处的河床形态通常比主深槽处更加复杂和不规则，导致水流的分流和流动扩散，这些因素都会提高测量的不确定性，导致与实际输沙率存在差异。

图6中结果出现差异的时刻点几乎均发生在急流时刻。朱文谨等［22］在对河口海岸水域泥沙垂线含沙量进行分析时，结合统计学方法采用多元线性回归分析各自变量对含沙量垂向分布的影响，然后对其加以修正项或可调系数以获得计算精度更高的结果。由于

机械误差、流速梯度、沉降速度差异以及局部水流扰动等多种因素，徐六泾断面在部分急流时刻的0.6H层含沙量与六点法计算得到的垂向平均含沙量存在一定差异。然而，上述平均相对误差计算结果显示，这种差异处于可接受的范围内，未来可以考虑加入流速和水流扰动的修正项，以更准确地估计垂线平均含沙量。

4.2  徐六泾上下游平均含沙量代表性分析

徐六泾断面作为长江口入海的重要节点，起着承上启下的重要作用，已有数据支撑下可以初步探究垂线平均含沙量代表层的表征规律。本文选取2016～2019年洪季的上游通州（TZS3、TZS4）和下游白茆沙（BMS1、BMS2）的数据进行假设检验，得到徐六泾河段上下游的假设检验结果（表4）。

白茆沙河段在2016～2019年间每年都有12个潮次，通州沙河段2016、2018年有10个潮次，2017年有8个潮次，2019年只有2个潮次。由表4可知，通州沙和白茆沙测站的数据经过假设检验后出现显著的差异，通州沙河段的假设检验结果明显优于白茆沙河段。这是由于地理位置的不同造成的，通州沙位于徐六泾上游，受外海潮汐的影响较小，而白茆沙则位于徐六泾下游，外海潮汐的影响显著。潮汐的涨落会导致河道水位和水流速度的变化，各层含沙量也会随之改变。在这种情况下，仅依赖0.6H层的数据来表征垂线平均含沙量可能不够准确。因此，有必要通过进一步的数据收集和研究，推导更为合理的公式以更准确地描述垂线平均含沙量。

5  结 论

本文通过对徐六泾断面及其上下游所测量的 0.6H层含沙量与垂线平均含沙量进行计算比较与分析，得到如下结论：（1） 在徐六泾断面，0.6H层含沙量可以表征垂线平均含沙量，其平均相对误差为（0±5）%，具有稳定性，LF假设检验结果也证明该结论成立。

（2） 徐六泾断面采用0.6H层单点法、三点法和六点法测得的单宽输沙率整体吻合效果较佳。大潮时差异略大，小潮时差异略小，1号垂线差异大于4号垂线。存在个别急流时刻，0.6H层单点法与六点法结果相差较大，未来可以考虑在计算垂线平均含沙量时加入水流扰动的修正项或使用三点法代替六点法。

（3） 徐六泾下游的白茆沙河段处0.6H层数据的代表性要劣于上游的通州沙河段，这是由于白茆沙河段受到外海潮汐的影响更加明显。

参考文献：［1］  张志忠.长江口细颗粒泥沙基本特性研究［J］.泥沙研究，1996，8（1）：67-73.

［2］  周昊，刘曙光.长江口徐六泾滩槽含沙量波动研究［J］.水资源研究，2023，12（1）：16-26.

［3］  李为华，李九发，张文祥.水体悬沙浓度连续测量技术研究综述［J］.热带海洋学报，2022，41（4）：20-30.

［4］  WANG C，YAO D J，HE B G，et al.Cross-shore suspended sediment ux in the salt marsh pioneer zone of Chongming eastern beach in the Changjiang estuary in China［J］.Acta Oceanological Sinica，2010，29（6）：62-72.

［5］  XIE D F，PAN C H，WU X G，et al.The variations of sediment transport patterns in the outer Changjiang estuary and Hangzhou bay over the last 30 years［J］.Journal of Geophysical Research：Oceans，2017，122（4）：2999-3020.

［6］  XIE Q C，YANG J，DAI W H，et al.Understanding morphodynamic changes of a tidal river confluence through field measurements and numerical modeling［J］.Water，2018，10（10）：1424-1444.

［7］  BOX W，VSTIL K，JRVEL J.The interplay between flow field，suspended sediment concentration，and net deposition in a channel with flexible bank vegetation［J］.Water，2019，11（11）：2250-2274.

［8］  GAO L，LI D J，DING P X.Quasi-simultaneous observation of currents，salinity and nutrients in the Changjiang （Yangtze River） plume on the tidal time scale［J］.Journal of Marine Systems，2009，75（1/2）：265-279.

［9］  YANG H F，LI B C，ZHANG C Y，et al.Recent spatio-temporal variations of suspended sediment concentrations in the Yangtze estuary［J］.Water，2020，12（3）：818-831.

［10］YANG H F，LI B C，YANG S L，et al.Impacts of large projects on the sediment dynamics and evolution of the Hengsha shoal in the Yangtze delta［J］.Ocean Engineering，2022，261（1）：1120-1133.

［11］QUAN X F，LI R J，LI Y T，et al.The influence of vertical velocity distribution on the calculation of suspended sediment concentration［J］.Discrete Dynamics in Nature and Society，2022，22（11）：1-15.

［12］刘传杰，朱巧云.长江口徐六泾断面近底悬沙测验及影响分析［J］.人民长江，2022，53（9）：87-93，101.

［13］张志林，高敏，廖建英.徐六泾站悬移质含沙量比测与精度分析［J］.人民长江，2010，41（6）：48-52.

［14］贺莉，陈东，段光磊，等.三峡大坝下游荆江河段悬沙浓度垂线分布研究［J］.泥沙研究，2020，45（6）：27-32.

［15］黄李冰，李义天，孙昭华，等.长江河口水流运动对悬沙分布的影响［J］.水力发电学报，2015，34（1）：55-62.

［16］ZHU W Q，ZHU M，ZHOU Z L，et al.Acoustic estimation of suspended sediment concentration［J］.Science in China，2001，44（8）：1064-1072.

［17］LU J Z，GUO X L，PAN J J，et al.Contrast analysis of flow-discharge measurement methods in a wide-shallow river during ice periods［J］.Water，2022，14（24）：3996-4014.

［18］RAZALI N M，WAH Y B.Power comparisons of Shapiro-Wilk，Kolmogorov-Smirnov，Lilliefors and Anderson-Darling tests［J］.Journal of Statistical Modeling and Analytics，2011，2（1）：21-33.

［19］罗文海，张庆凤.定量数据SPSS正态性检验影响因素探讨［J］.中国医院统计，2018，25（4）：283-286.

［20］NEUHUSER M.Combining the t test and Wilcoxon′s rank-sum test［J］.Journal of Applied Statistics.2015，12（42）：2769-2775.

［21］张幸农，陈长英，刘慧.论感潮河段航运工程水文标准分界与衔接［J］.水科学进展，2015，26（5）：707-713.

［22］朱文谨，潘锡山，孙杰.基于Rouse方程的河口海岸水域泥沙垂线浓度分析［J］.河海大学学报（自然科学版），2012，40（2）：215-219.

（编辑：胡旭东）

Representative layer of vertical mean sediment concentration at Xuliujing Station of Yangtze River Estuary

JIANG Xuan1，WEN Weidong2，ZHI Yuanzhe3，LIU Chuanjie2，SHAO Yuyang1

（1.College of Harbour，Coastal and Offshore Engineering，Hohai University，Nanjing 210024，China;

2.Yangtze River Estuary Investigation Bureau of Hydrology and Water Resources，Changjiang Water Resources Commission，Shanghai 200136，China；

3.Institute of Water Science and Technology，Hohai University，Nanjing 210024，China）

Abstract：

For estuaries of big rivers with large water depth and heavy traffic，it is impossible to carry out traditional six-layer sampling measurement for sediment concentration.How to obtain more accurate vertical average sediment concentration and improve the measurement accuracy of sediment flux into the sea is the focus of current scholars.Taking the Xuliujing hydrological corss-section as an example，a key node of the Yangtze River Estuary，the average sediment concentration of the vertical line was calculated by a variety of hierarchical combination methods，and the confidence interval，average relative error and Lilliefors hypothesis test were used for calculation and analysis.At the same time，combined with the upstream and downstream hydrological corss-sections data of the observation node，the characterization law of the vertical average sediment concentration representative layer was preliminarily clarified.It was found that although the Xuliujing hydrological cross-section is affected by the runoff-tide interaction，the 0.6H layer was proved to be the best representative layer，and the average relative error of the observation results was in the range of （0±5）%.However，in the south branch of the lower reaches，the hydrological cross-section of Baimaosha was significantly affected by tidal dynamics，resulting in poor representation of 0.6H single layer.The research results have important guiding significance for the future transformation of hydrological integrated buoys and the accurate acquisition of sediment flux from the Changjiang River to the sea.

Key words：

sediment concentration; representative layer; Lilliefors hypothesis testing; error analysis; Xuliujing hydrological cross-section; Yangtze River Estuary