基于大涡模拟的风琴管喷嘴结构参数优化及流动特性分析

杨新霞 闫月娟 徐艳 李森 刘海水 刘幸倩

DOI：10.20031/j.cnki.0254?6094.202403009

摘 要 基于ZGB空化模型和WALE亚格子模型，采用大涡模拟（LES）方法对风琴管喷嘴空化射流流场进行数值模拟研究，在实验与数值模拟空化云演化规律基本吻合的基础上开展风琴管喷嘴结构参数优化设计。基于三因素四水平的正交试验设计，分析了圆柱段及扩散段对空化射流流场特性的影响规律。结果表明，扩散角角度为空化效果的主要影响因素，圆柱段长度为射流效果的主要影响因素，扩散段长度对空化射流影响相当，通过极差分析获得了风琴管喷嘴最优结构参数组合。对比分析风琴管喷嘴结构参数优化前后的空化射流流场发现，优化后的风琴管喷嘴空化射流效果显著提升。

关键词 风琴管喷嘴 大涡模拟 正交试验 结构参数优化 空化射流

中图分类号 TQ055   文献标志码 A   文章编号 0254?6094（2024）03?0382?10

Large Eddy Simulation?based Optimization of

Organ Nozzle Structural Parameters and Flow Characteristics Analysis

YANG Xin?xia， YAN Yue?juan， XU Yan， LI Sen， LIU Hai?shui， LIU Xing?qian

（School of Mechanical Science and Engineering， Northeast Petroleum University）

Abstract   Based on ZGB cavitation model and WALE subgrid model， having large eddy simulation （LES） method adopted to simulate cavitation jet flow field of the organ nozzle was implemented， including basing on the general coincidence between experimental and numerical simulation of the evolution law of cavitation clouds to optimize the organ nozzles structure parameters. In addition， based on orthogonal experimental design of three factors and four levels， the influence of both cylindrical and diffusion sections on the cavitation jet flowfield characteristics was analyzed to show that， the diffusion angle mainly influences cavitation effect， and the cylindrical sections length mainly influence jet effect， and the diffusion sections length has a similar effect on the cavitation jet. Through analysis of range， the optimal structural parameters combination of the organ nozzle was obtained. Comparing and analyzing the cavitation jet flowfield simulated before and after optimizing structural parameters of the organ nozzle indicates that， the optimized organ nozzle has significantly improved the cavitation jet effect.

Key words   organ nozzle， large eddy simulation， orthogonal experiment， structural parameter optimization，cavitation jet

（Continued from Page 359）

基金项目：黑龙江省自然科学基金（批准号：LH2022E016，LH2022A004）资助的课题。

作者简介：杨新霞（1997-），硕士研究生，从事机器学习与空化射流数值模拟研究。

通讯作者：闫月娟（1971-），教授，从事流体机械及内流特性的研究，1072254366@qq.com。

引用本文：杨新霞，闫月娟，徐艳，等.基于大涡模拟的风琴管喷嘴结构参数优化及流动特性分析[J].化工机械，2024，

51（3）：382-391.

高压水射流清洗领域中[1～4]，风琴管空化射流喷嘴利用空泡溃灭产生的高温高压可以大幅提高射流的冲击效果，因此近年来得到了广泛应用。在绿色低碳发展的大背景下，一些石油化工设备由于所处理介质的复杂性，导致产生的污油或垢蚀难以清洗，因此优化设计一种更加高效节能的风琴管喷嘴结构尤为重要。

风琴管喷嘴空化射流具有强烈的多相湍流特征[5]。目前，大多数学者采用RANS方法对风琴管喷嘴进行数值模拟研究，然而RANS模型的涡黏假设仅能对时均化流动进行模拟，缺少瞬时流场信息对空化射流流动的影响。大涡模拟（LES）在求解过程中对大尺度的涡直接求解，对小尺度的涡建模，因此在理论上模拟精度优于RANS模型。王连安等基于大涡模拟方法对风琴管空化喷嘴流场进行数值模拟，发现大涡模拟可以更好地捕捉圆柱段以及扩散段的涡环分布[6]。李贵东等采用大涡模拟方法对射流式离心泵射流器进行研究，并与SST k?ω湍流模型的模拟结果进行对比，结果表明，基于时间平均的SST k?ω湍流模型无法很好地模拟泵喉管内部的压力脉动情况，大涡模拟结果则能得到压力脉动随时间的变化，且与试验结果一致[7]。暴春航等利用大涡模拟对推进装置的强剪切空化射流特性进行了数值模拟研究，结果表明，大涡模拟可以捕捉到外流场涡分布以及空化云演变规律。因此，大涡模拟可以更准确地模拟空化射流流场[8]。

空化喷嘴作为典型的空化发生器，其流道结构参数对射流空化程度、空化效果影响巨大。大涡模拟准确度高但计算成本也高，因此针对空化喷嘴结构参数优化问题，大多数学者采用k?ε湍流模型进行数值模拟研究。王萍辉和方湄验证了风琴管自激振荡空化喷嘴的清洗效果与喷嘴谐振腔的直径、长度以及靶距都有关，同时也验证了用理论公式设计风琴管喷嘴结构是可靠的[9]。郭世建根据理论公式确定了圆柱段直径，同时入口段与谐振腔的尺寸可根据最佳长径比确定，采用RNG k?ε模型对风琴管喷嘴圆柱段长度、扩散段长度、扩散角和靶距进行了结构参数优化，得到了最佳参数组合[10]。杨涵根据自振空化射流喷嘴的基本结构，采用RNG k?ε模型对其主要结构参数（如喷嘴扩散角、扩散段长度及圆柱段长度等）对喷嘴性能的影响进行了分析，得到了最佳参数组合[11]。CAI T F等对风琴管喷嘴结构参数进行了实验研究，结果表明，当扩散角为10～25°时空化效果最好[12]。

综上所述，LES模型可以更好地捕捉涡环分布和空化云演变规律，采用LES方法可以更精确地优化风琴管喷嘴结构参数，从而提高清洗效率。当压力不同时，优选出的最佳结构参数可能不同，为此，笔者采用数值模拟研究方法在12 MPa低压工况下进行风琴管喷嘴结构参数优化。根据理论公式确定圆柱段直径，借鉴已有的研究成果，采用大涡模拟方法对风琴管喷嘴圆柱段长度、扩散段长度和扩散角角度进行参数优选。对比分析优化前后的风琴管喷嘴空化射流流场特性，从而验证优化后的风琴管喷嘴结构空化效果，获得低压高效节能的风琴管喷嘴结构参数。

1 物理模型

1.1 计算模型

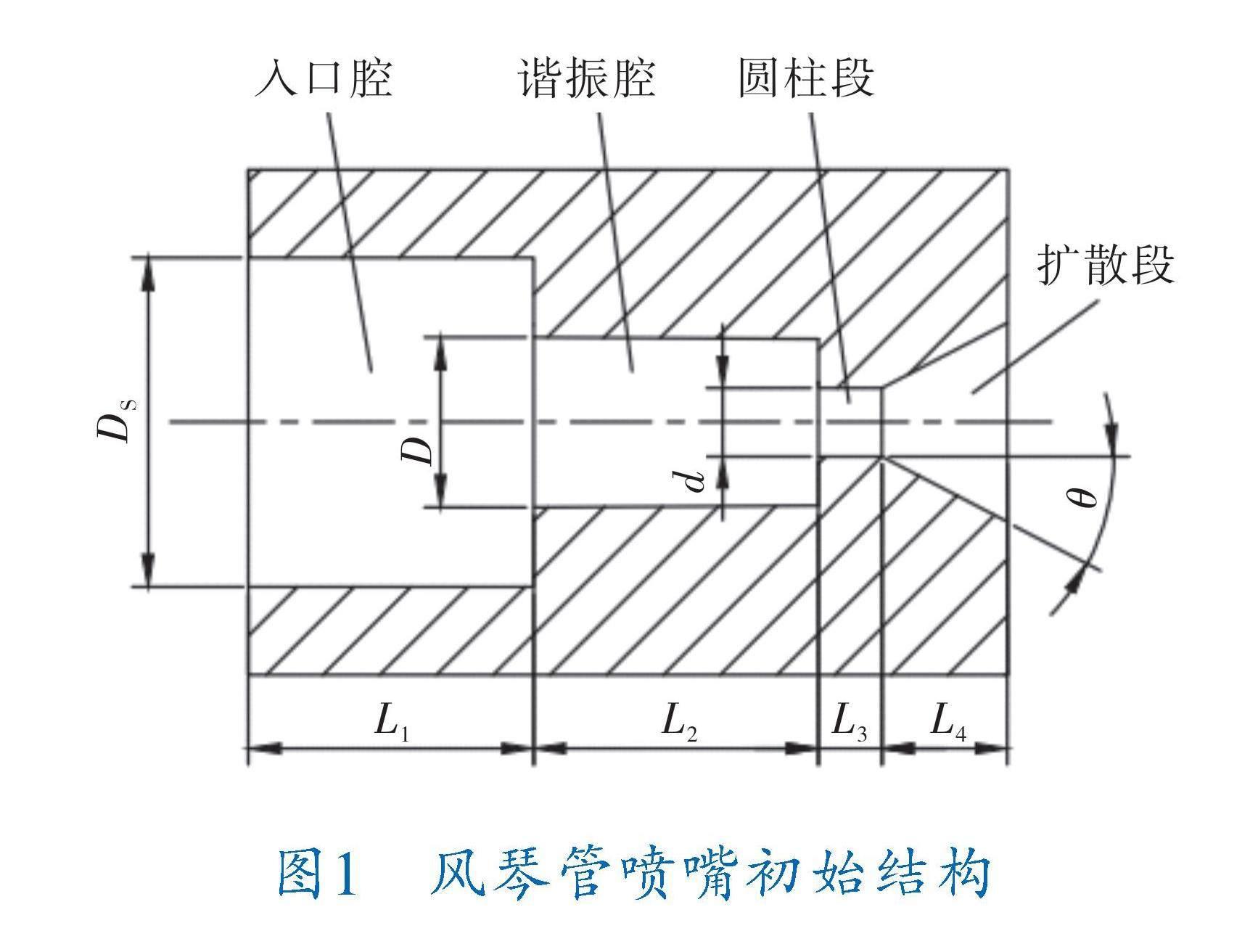
根据蔡腾飞等对风琴管喷嘴结构的优化结果[13]，结合实际清洗应用情况，确定了喷嘴初始结构（图1），主要包括入口腔、谐振腔、圆柱段和扩散段，尺寸参数如下：

入口直径D 6.4 mm

谐振腔直径D 3.2 mm

圆柱段直径d 1 mm

入口长度L 5.2 mm

谐振腔长度L 5 mm

圆柱段长度L 1 mm

扩散段长度L 2 mm

扩散角角度θ 15°

1.2 网格划分

为保证喷嘴入口来流的充分发展，将入口长度向上游延长至5倍入口直径，即32 mm。为使流场充分发展，所将喷嘴外部设置为出口段，出口段属于外流场研究区域。为了避免出口处产生回流从而影响射流区域，将出口长度设为80 mm，直径为20 mm。风琴管喷嘴空化射流流体计算域如图2所示。

用ICEM软件建模，对流体域进行结构性网格划分，网格单元为六面体。由于圆柱段、扩散段部位属于发生空化射流的核心区域，所以进行加密处理。网格无关性验证如图3所示，网格节点数量分别为72万、188万、307万和420万。通过对比模拟后的最大气相体积分数可以发现，当网格数量增加到307万时，最大气相体积分数变化不超过2%。综合考虑计算精度与时间成本，最终选择307万网格数作为后续计算模型，其网格划分如图4所示。

2 控制方程与模拟参数设置

2.1 大涡模拟控制方程

大涡模拟通过滤波函数将湍流的瞬时运动分解成大尺度涡与小尺度涡，将连续性方程与动量方程滤波后得：

+=0（1）

+=-+（μ-τ）（2）

τ=-2μS+τδ（3）

其中，ρ为混合相密度，[u][～]、[u][～]为i、j方向滤波后的速度分量，[p][～]为滤波后的压力，μ为混合相动力黏度系数，τ为亚格子应力项，S为平均应变率张量，δ为Kronecker delta（克罗内克）函数，τ为亚网格尺度应力的各向同性部分。

2.2 空化模型

选择合适的空化模型对准确描述空化喷嘴内部流场具有重要影响。依据文献[14]的相关研究，Zwart?Gerber?Belamri（ZGB）模型计算精度高，适用于描述复杂流场，且具有较好的收敛性，其蒸发率R与凝结率R表达式如下：

R=F（4）

R=F （5）

其中，F为蒸发率系数，α为气泡体积分数，α为气相体积分数，ρ为气相密度，R为气泡半径，p为饱和蒸气压，p为局部压力，ρ为液相密度，F为凝结率系数。

2.3 模拟参数设置

空化射流属于气液两相流动，气相为水蒸气，液相为25 ℃的水，液相密度1 000 kg/m3，饱和蒸汽压3 169 Pa。使用双精度压力基求解器进行数值模拟，多相流采用Mixture模型，壁面无滑移速度。空化模型选ZGB模型，亚格子模型选用壁面适应的局部涡黏（WALE）模型。边界条件分别为压力入口和压力出口，入口压力12 MPa，出口压力为大气压，连续性曲线收敛精度10-5。选用Coupled算法进行速度-压力耦合，瞬态项方程采用Bounded Second Order Implicit，压力项为PRESTO！方法，初始化方式选用全局初始化，时间步长设置为10-5 s。

3 数值模拟与实验空化云对比

游离型空化泡溃灭时，近壁处产生微射流，从而产生速度快、打击力强的高压脉冲以实现对污垢的清洗。因此，通过分析空化云演变规律可以预测喷嘴清洗效率。在进行数值模拟时，时间步长设为10-5 s，每10步自动保存一次，即每0.1 ms记录一次空化云状态。空化射流实验台主要由储水箱、柱塞泵、压力表、风琴管喷嘴、实验水箱及高速摄像机等组成，根据已有实验研究设置实验具体参数[6]。为保证空化云发展周期与模拟时间保持一致，高速摄像机曝光时间设为100 μs，拍摄频率为10 000 fps（1 fps=0.304 m/s）。数值模拟结果与实验研究空化云演变规律如图5、6所示。

空化云的发展具有连续的周期性，具有初生期、发展期、脱落期和溃灭期4个阶段，从图5、6可以看出，空化云开始脱落的时间为0.0、0.8、

1.6 ms，脱落周期在0.8 ms左右。0.0～1.5 ms是一个完整的空化云演变周期，空化泡在0 ms时产生，在0.1～0.7 ms时间段内属于发展期，在0.8 ms开始脱落，脱落后的空化云不断溃灭直至1.5 ms后消失。将数值模拟结果与实验研究对比发现，LES模型空化云分布情况与实验结果基本吻合，验证了笔者所建立的LES空化射流数值计算模型可以准确地模拟风琴管喷嘴空化射流规律。下面采用LES模型进行正交试验优选喷嘴结构参数。

4 正交试验

4.1 正交试验因素水平及指标确定

正交试验设计利用正交性挑选出具有代表性的点进行试验，是一种高效率的试验设计方法，其利用较少的试验次数即可得到最优的结构参数组合[15]。笔者采用正交试验方法进行数值模拟分析，从而更准确地找到风琴管喷嘴结构参数最优组合。

风琴管喷嘴的圆柱段直径是确定其他参数的依据[16]。圆柱段直径的最佳理论公式为：

d=（）×1.05-b（6）

其中，q为泵的额定流量，p′为泵的额定压力，n为喷嘴个数，修正系数b的范围为0.1～0.3。代入相关数据计算可得d=1 mm。

圆柱段直径与压力值确定后，研究圆柱段长度、扩散段长度和扩散角角度对空化射流的影响，并对这3个参数进行模拟优选[11]。从空化效果与射流速度两方面评价喷嘴清洗性能。圆柱段和扩散段为空化产生的核心区域，该位置的空泡含量影响着空化作用的强弱，因此选取核心区域位置的最大气相体积分数作为评价结构性能的指标。同时，空泡溃灭产生的射流速度是打击力的关键参数，从而影响清洗效果，因此将选取目标靶距的平均射流速度作为评价结构性能的指标。

设计采用三因素四水平（表1）的正交试验法来确定影响清洗效果的主次因素。

4.2 试验结果分析

根据正交试验设计方案，采用大涡数值模拟方法对16组试验进行数值模拟研究，通过试验指标的极差分析得到最优参数组合。

4.2.1 最大气相体积分数极差分析

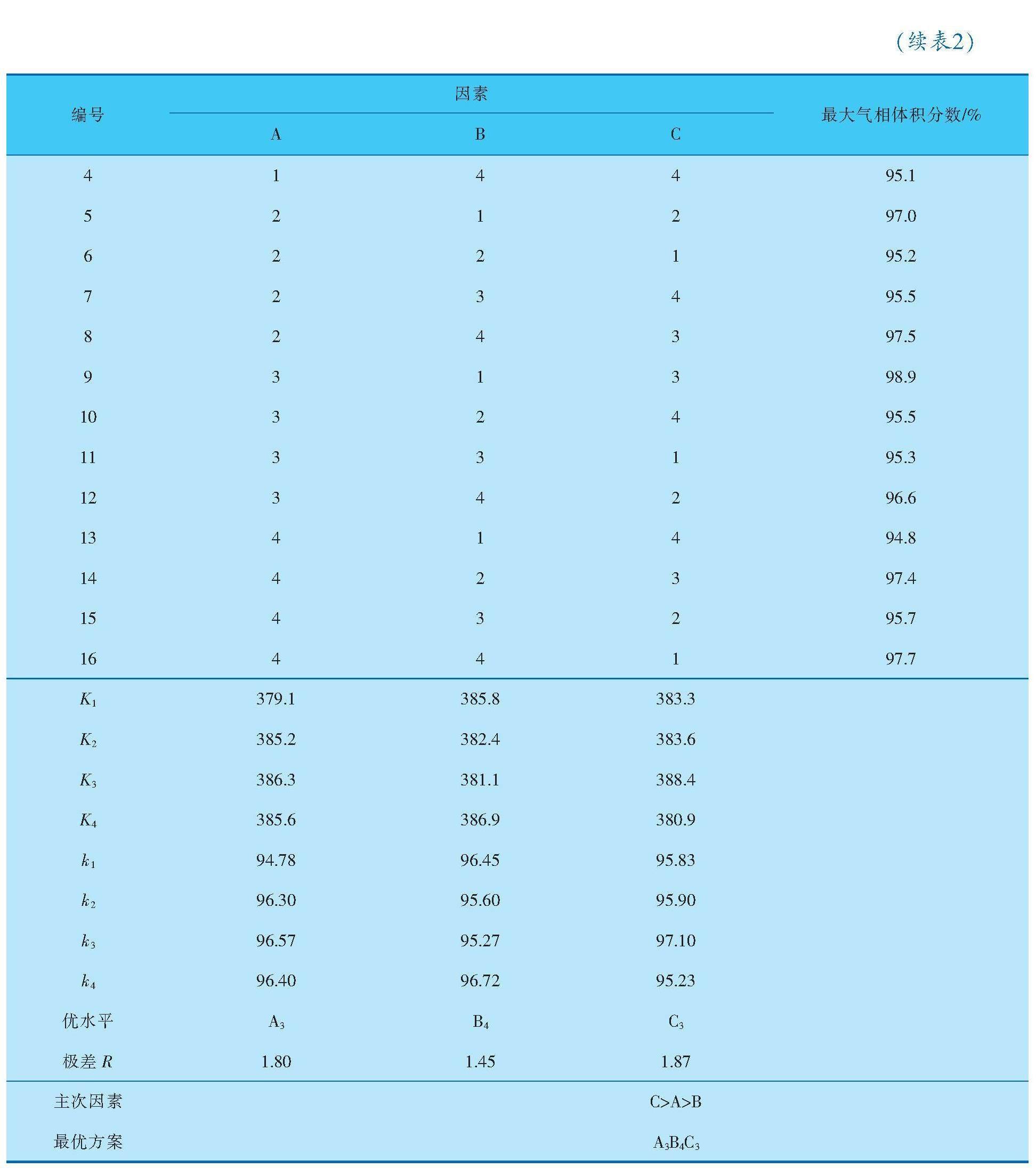
最大气相体积分数极差分析结果见表2。

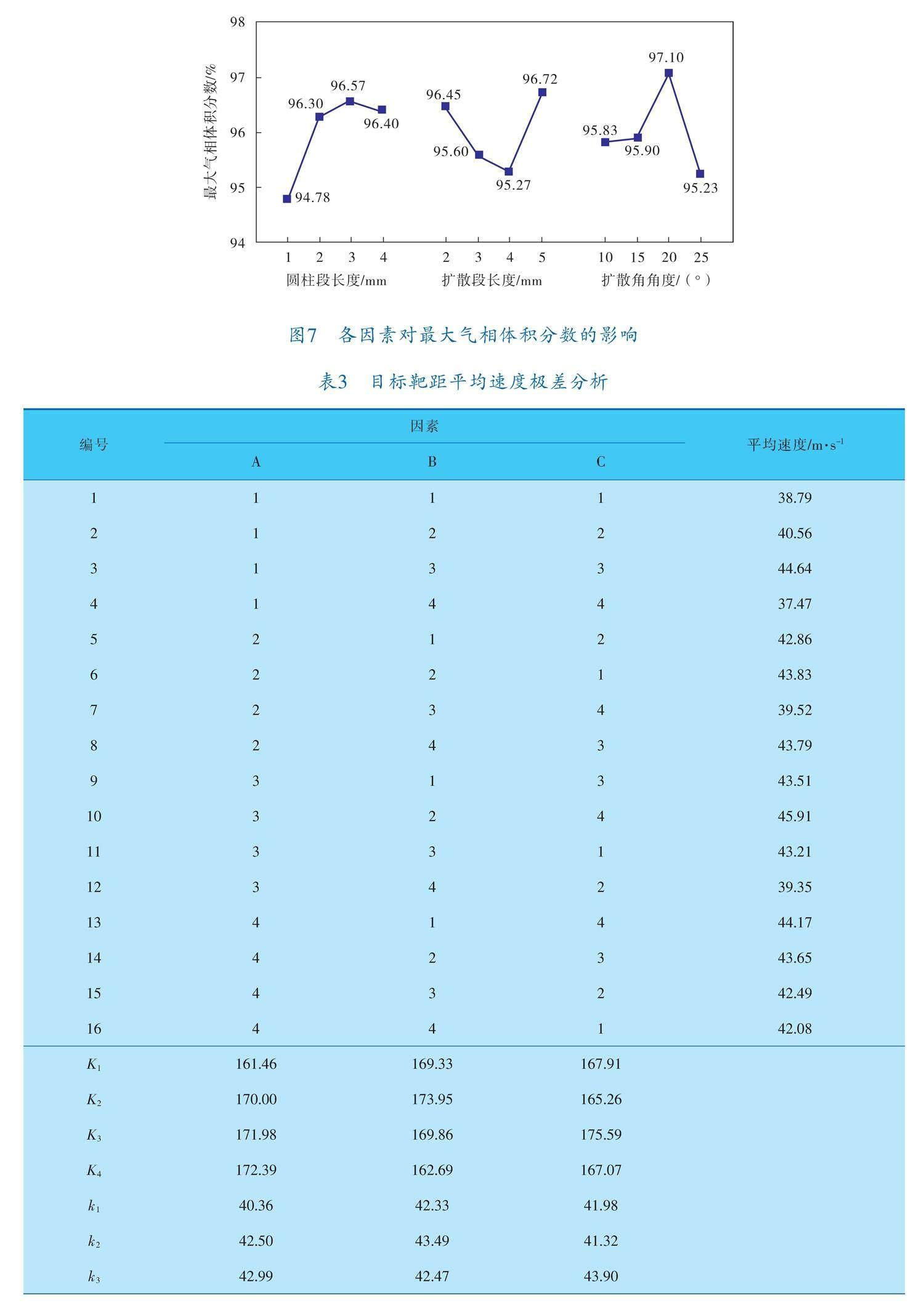
三因素各水平下的最大气相体积分数如图7所示。可以看出，扩散角角度（因素C）为最大气相体积分数的主要影响因素，其值呈现先增大后减小的趋势，在水平3时，气相体积分数达到最大值，为97.10%;圆柱段长度（因素A）为最大气相体积分数的次要影响因素，其值呈现先增大后减小的趋势，在水平3时，气相体积分数达到最大值，为96.57%;扩散段长度（因素B）为最弱影响因素，最大气相体积分数呈现先减小后增大的趋势，在水平4处达到最大值，为96.72%。

因此，当最大气相体积分数为性能检测指标时，最优参数结构的组合为A3B4C3，即最优方案。

4.2.2 目标靶距平均速度极差分析

针对内径62 mm的管道清洗时，目标靶距选取12 mm，射流打击力大小由目标靶距位置射流速度决定，因此分析出口位置12 mm处平均速度极差情况，结果见表3。

三因素各水平下的平均速度如图8所示。可以看出，随着圆柱段长度的增加，目标靶距位置处平均速度也逐渐增大，在水平4处平均速度达到了最大值，为43.10 m/s;随着扩散段长度的增加，目标靶距位置处的平均速度呈出出先增大再减小的趋势，在水平2处平均速度达到了最大值，为43.49 m/s;随着扩散角角度的增加，目标靶距位置处平均速度先减小后增大再减小，在水平3处平均速度达到最大值，为43.90 m/s。其优选出的组合分布与极差分析一致，因此，当平均速度为性能检测指标时，最优参数结构组合为A4B2C3，即最优方案。

4.2.3 风琴管喷嘴最优结构参数

圆柱段长度（因素A）对最大气相体积分数与平均速度的影响相当，但最大气相体积分数是产生空泡的主要原因，而空泡含量决定了空化作用的强弱，从而对清洗效率产生重要影响，因此选用A3作为最优结果。扩散段长度（因素B）为平均速度影响的主要因素，是最大气相体积分数影响的次要因素，平均速度影响着打击力的大小，因此选用B2作为最优结果。扩散段角度（因素C）是最大气相体积分数影响的主要因素，是平均速度影响的次要因素，由于最大气相体积分数间接性地决定了空化的强弱，因此选取C3作为最优结果。

综上，风琴管喷嘴最优结构组合为A3B2C3，具体参数如下：

圆柱段长度 3 mm

扩散段长度 3 mm

扩散角角度 20°

5 喷嘴结构优化前后流场对比

5.1 压力场

5.1.1 压力云图

当射流过程中局部气压低于相对温度下水的饱和蒸气压时，部分液体由液态转变为气态产生“空泡”，压力增大到一定程度时，空泡集中破裂产生“空化”现象。因此喷嘴内外流场的压力分布影响着喷嘴的空化效果。结构参数优化前后模拟得到的负压云图如图9所示。图9显示扩散段至出口位置均有负压产生，其中，中心区域为负压最大区域，压力达到-97.8 kPa。优化后的结构负压区主要在喷嘴出口轴向位置66.8 mm内，负压范围为-97.8～-69.8 kPa，压力波动比较明显，负压大且波及范围广。初始结构负压区主要在出口轴向位置59.3 mm内产生，除中心区域外，负压范围主要集中在-69.8～-41.9 kPa，负压值与负压范围均较小。负压大有利于空化产生，负压范围大有利于空化泡发展，因此优化后的结构空泡更多，发展更充分。

5.1.2 目标靶距位置压力分布

在目标靶距位置径向上创建一条过圆心的线段，近壁面总压为0，因此截取-5～5 mm区域观测压力分布情况，优化前后风琴管喷嘴模拟的压力分布曲线如图10所示。可以看出，优化前后压力分布呈尖塔形状，分布比较集中，均处于中心位置处。优化前的喷嘴最大压力为10.8 MPa，优化后最大压力为12.0 MPa。因此，优化后的风琴管喷嘴打击力更大，清洗效率更高。

5.2 速度场

5.2.1 速度云图与矢量图

速度云图及矢量图分布如图11所示。可以看出，喷嘴优化前后的核心位置处速度均达到

160 m/s并产生射流。随着射流卷吸、附面层分离和空泡的产生、长大与破裂，射流影响区域不断增大。压力与速度发生振荡在矢量图中体现为涡流。初始结构模拟的速度矢量主要在径向9.8 mm范围内发生振荡，但振荡不明显。优化后的喷嘴结构模拟得到的流场径向16.6 mm范围内有明显振荡。因此，优化后的喷嘴空化射流流场产生涡量更多。

5.2.2 轴线速度分布

优化前后风琴管喷嘴空化射流流场的轴向速度分布曲线如图12所示。可以看出，两种喷嘴结构在入口段轴向速度均无明显变化，谐振腔处直径由6.4 mm缩减至3.2 mm，因此速度均轻微增大。圆柱段直径缩小至1 mm后，速度均急剧增大到最大值160 m/s，产生射流现象，并在喷嘴出口附近出现了明显的等速段。优化后的喷嘴模拟得到的等速段长度约为初始结构的1.27倍，等速段越长，射流速度越高。在喷嘴出口位置附近初始

结构速度最小值为20 m/s，优化后的结构速度最小值为47 m/s。在喷嘴出口位置附近，优化后的喷嘴模拟得到的轴向速度值振荡更明显，涡量更多。因此，优化后的喷嘴在射流过程中，由于速度较大从而产生了更大的打击力，提高了清洗效率。

5.2.3 外流场不同位置速度分布

优化前后风琴管喷嘴空化射流流场在x=

50 mm与x=80 mm位置径向速度变化曲线如图13所示。可以看出，x=50 mm位置处，由于流体高速流出喷嘴且形成等速核，因此振荡不明显。初始结构速度达到158 m/s，但射流宽度仅为2.5 mm。优化后的结构速度为155 m/s，在峰值处有轻微振荡，射流宽度约6 mm，极大地提高了清洗效率。在x=80 mm位置处，由于流体在出口位置充分发展，因此会向边壁发散，从而引起速度振荡。初始结构模拟的速度为45 m/s，振荡范围较小，仅在径向-2.5～2.5 mm之间有轻微振荡。优化后的喷嘴速度为92 m/s，在径向-5～5 mm范围内有明显振荡。因此，优化后的结构有更多涡产生，空化作用更强。

5.3 空化云对比分析

优化前后同一时刻的气相分布云图如图14所示。可以看出，优化后的喷嘴结构模拟得到的空化云长度约89.8 mm，宽度为12.3 mm。初始结构的喷嘴模拟得到的空化云长度约80.2 mm，宽度为9.2 mm。空化云长度与宽度决定了喷嘴清洗范围与有效清洗面积。因此，优化后的风琴管喷嘴空化效果显著提高。

6 结论

6.1 采用LES数值模拟方法，基于三因素四水平正交试验设计，通过极差分析得到最优结构是圆柱段长度为3 mm，扩散段长度为3 mm，扩散角角度为20°。

6.2 通过对比分析风琴管喷嘴结构参数优化前后的压力场可知，优化后的结构负压区集中在出口段66.8 mm内，初始结构负压区集中在出口段59.3 mm内。优化后的喷嘴空化云发展更充分。

6.3  通过对比分析风琴管喷嘴结构参数优化前后的速度场可知，优化后的结构等速核长度约为初始结构的1.27倍，等速段越长射流速度越高。优化后的喷嘴射流速度更大，对管道清洗更加有利。

6.4 通过对比分析风琴管喷嘴结构参数优化前后的气相分布云图可知，优化后的结构较初始结构的空化云长度增加了9.2 mm，宽度增加了

3.1 mm。优化后的喷嘴空化云长度、宽度都有所增加，因此空化效果更好，有效清洗面积与清洗效率更高。

参 考 文 献

[1] 李根生，沈忠厚.常压下淹没自振空化射流冲蚀岩石效果的试验研究[J].华东石油学院学报（自然科学版），1987（3）：12-22.

[2] 吴同锋，蔡晓君，刘湘晨，等.基于高压水射流的管道清洗方案设计[J].化工机械，2017，44（1）：43-46.

[3] 刘峰，朱南文，王亚林，等.射流空化技术处理乳化含油废水的研究[J].石油与天然气化工，2005，34（5）：416-419.

[4] 庞雷，王永强，鲁飞，等.钻井泥浆罐自动化清洗与回收成套设备研制[J].流体机械，2020，48（7）：12-15;21.

[5] DESANTES J M，PAYRI R，SALVADOR F J，et al.Influence of cavitation phenomenon on primary break?up and spray behavior at stationary conditions[J].Fuel，2010，89（10）：3033-3041.

[6] 王连安，徐艳，王尊策，等.风琴管喷嘴空化水射流流场的大涡模拟[J/OL].机械科学与技术：1-10[2024-05?03].https：//doi.org/10.13433/j.cnki.1003?8728.2023

0072.

[7] 李贵东，王洋，杨学明，等.基于大涡模拟的射流式离心泵射流器内部的流动特性[J].排灌机械工程学报，2017，35（5）：369-374.

[8] 暴春航，龙新平，梁蕴致，等.高压水射流喷水推进装置空化流动及推力特性仿真分析[J].液压与气动，2023，47（1）：32-43.

[9] 王萍辉，方湄.空化水射流清洗的实验研究[J].煤矿机械，2004（1）：37-40.

[10] 郭世建.基于空化射流的油管内壁清洗技术研究[D].沈阳：东北石油大学，2018.

[11] 杨涵.空化射流喷嘴流场数值模拟研究[D].成都：西华大学，2015.

[12]   CAI T F，PAN Y，MA F.Effects of nozzle lip geometry on the cavitation erosion characteristics of self?excited cavitating waterjet[J].Experimental Thermal and Fluid Science，2020，117：110137.

[13] 蔡腾飞，潘岩，马飞，等.喷嘴出口结构参数对风琴管射流空化作用的影响[J].机械工程学报，2019，55（18）：150-156.

[14] 曹东刚，何国强，潘宏亮，等.三种空穴模型在可调汽蚀文氏管数值模拟中的对比研究[J].西北工业大学学报，2013，31（4）：596-601.

[15] 李云雁，胡传荣.试验设计与数据处理[M].第2版.北京：化学工业出版社，2008.

[16] 李根生，沈忠厚，周长山，等.自振空化射流研究与应用进展[J].中国工程科学，2005，7（1）：27-32.

（收稿日期：2023-04-21，修回日期：2024-05-07）