基于Wi-Fi 的移动目标角度估计算法研究

田利平　李维弦

摘要：考虑到MUSIC算法在实际应用场景中，因为相干和分辨力低而无法满足实际需要。文章提出了一种基于信号空间分解的动态，静态信号分离算法。充分分析了人体运动，产生的反射信号之间的相干性，该算法将信号协方差矩阵特征空间分解后，最大特征值和其对应的特征矢量形成的空间为静态信号空间，其余的为动态信号空间。再用信号空间的MUSIC算法来估计静态路径信号和动态路径信号的到达角。通过仿真实验和真实环境验证了文章算法的有效性。

关键词：CSI；特征值；AOA；TOF；相干

中图分类号：TP311 文献标识码：A

文章编号：1009-3044（2024）13-0127-05 开放科学（资源服务）标识码（OSID） ：

0 引言

准确的估计信号的波达方向，一直是通信领域研究的热点问题。例如在军事领域，需要准确探测敌方飞行器的方向；在老人和小孩的监护方面可以通过他们的运动方向实现准确定位，从而实施精准的救护措施。最早的到达角的估计是使用机械扫描的方式，需要花费大量的时间，而且准确度不高。波束形成算法[1]是最早的到达角估计算法。这种算法主要是利用空域的阵列信号，代替时域傅里叶变换的时域信号。该局限性在于入射信号的角度差小于波束宽度时，该算法就完全失效（等同于傅里叶变换的限制）。要想增加分辨力，即需增加阵列信号的孔径，这无疑会增加成本。因为空间信号的到达角估计与时域频率估计非常类似，所以时域频率估计的非线性算法被推广而成为空间信号的到达角估计，例如最大熵法[2]和最小方差法[3]。这些方法虽然叫作高分辨谱估计方法，但是它们假定信号源在空间中是连续分布的，但实际中这样的假设是不成立的。针对以上问题，文献[4]提出的多重信号分类MUSIC）算法，它是空间谱（M估ult计ipl的e 一Sig次na飞l 跃Cla，s它sif打ica破tio了n，瑞利限，实现了超高分辨率的角度估计，而且充分利用了信号的统计特性。它主要利用信号的协方差矩阵，进行特征分解，得到信号空间和噪声空间，利用信号空间和噪声空间的正交性，得到针状谱峰，从而大大提高了算法的分辨力。利用MUSIC算法或者特征空间的信号到达角估计算法成为研究热点。

室内定位技术已在多个领域得到发展和应用，2017年其商业利润达到100亿美元[5]。例如，它可以帮助定位医院中的患者并诊断抑郁症、躁狂症等。在儿童的家庭护理和监督中，它可以用来调节异常行为。在大型仓库中，它可以定位货物和贵重物品。在工业区发生突发灾害时，还能帮助救援人员及时找到被困人员。因此，各种室内定位技术被开发出来。例如，基于蓝色线齿的室内定位技术已经被提出[6-7]，尽管其应用通常仅限于十米左右的小范围。利用超声波的室内定位技术已在文献[8-9]中提出。但室内多径对定位精度影响较大，且超声波易受环境温度和多普勒效应影响。超宽带技术也已用于室内定位[10-11]，但其成本相对较高，尚未得到广泛应用。基于RFID 的室内定位技术也已有描述[12-14]，但其抗干扰能力通常较差。随着Wi-Fi信号的普及，利用它们进行室内定位已经得到研究和开发[15-17]。Wi-Fi定位和跟踪算法可以分为两种类型。第一种是主动定位或跟踪，例如 SpotFi[18]、Wicapture [19] 和 Milliback [20]，但它们需要人们随身携带设备，不方便。第二种技术是无源定位或跟踪。主要有两种被动跟踪算法：（1） 基于指纹的跟踪算法；（2） 基于参数的室内跟踪算法。基于指纹的跟踪算法提前收集大量样本并用它们来训练算法。它们需要大量的能量和资源。CSI-MIMO[21]利用CSI 信号的幅度和相位信息构建指纹数据库从而实现定位。Chen等人[22]为了用Wi-Fi设备实现厘米级的精度，提出了一种基于时间反转的指纹算法室内定位算法，它充分利用了多输入多输出（MIMO）Wi-Fi算法的空间多样性，获得比Wi-Fi 信道更宽的有效带宽。Pinloc[23]是一种基于CSI 信号的概率局部定位算法。该算法的原理：CSI信号在每个地点都不是完全随机。文献[24]考虑到基于接收信号强度RSS测出的距离估计容易受到多径效应的影响，而提出了一种新的方法FILA，利用信道状态信息（CSI）在接收端建立传播模型并用指纹识别算法实现定位。MonoPHY[25]仅用单Wi- Fi链路采集的CSI信号的幅度，使用极大似然概率估计算法，在面积约100平方米的典型公寓中的35个不同位置构建整个区域的指纹数据。随着人工智能与深度学习的发展，很多研究人员将深度学习应用于指纹定位，得到了较好的结果[26-31]。但是由于传统的指纹定位算法受环境影响较大，室内家具位置改变、空气的温度、湿度、窗户的关闭状态均会影响CSI信号，而这些因素一旦发生变化，就需重新采集指纹数据，这将花费大量人力物力。为了应对环境变化引起的指纹退化的问题，许多学者采用了基于参数估计的室内定位算法。

Widar2.0[32]使用了不同天线的CSI信号的共轭相乘来得到动态路径，再使用极大似然算法的AOA，TOF，多普勒速度，幅度联合估计，可以得到较为准确的角度信息，但该算法不能遮挡直射路径，否则算法失效。Dynamic-music[33]通过分析了人体运动时，动态路径和静态路径之间的相干性，提出了静态路径会合并为一条。即先使用MUSIC算法，再把动态路径找出来。但是由于人体运动过程中躯干部分反射的信号之间是相干的，所以认为动态路径之间是不相干的说法是不正确的。而MUSIC算法对相干信号是完全失效的。MUSIC算法在实际信噪比较低的情况下，角度分辨力很低，动态路径和静态路径的角度会合并成一个而无法区分。如果可以把静态路径信号和动态路径信号分开处理，那么上述问题迎刃而解。在很多种情况下，我们只需要研究感兴趣的信号。例如，在轨迹跟踪过程中，我们希望得到由人体运动产生的信号，而对于地面，家具，墙壁等的反射信号一般与动态信号是比较难分离的。在OFCW雷达感知识别过程，通常要用到CFAR，其主要通过相邻时间窗内，信号变化的大小去除静态信号。但由于Wi-Fi信号频率较低，且用于通信的Wi-Fi信号会对CSI造成干扰，所以若用CFAR类似的算法，很难实现。为了解决上述问题，我们提出了一种新的动态路径和静态路径的到达角估计算法。该算法可以在被动状态下，准确提取目标反射信号的角度，而且在动态路径相干的情况下也可以识别。该算法将信号协方差矩阵特征空间分解后，最大特征值和其对应的特征矢量形成的空间为静态信号空间，其余的为动态信号空间。再用信号空间的MUSIC算法来估计静态路径信号和动态路径信号的到达角。在仿真和真实的环境下，均有较好的效果。

1 理论基础

1） 静态路径之间是相干的，因为不同的反射路径之间只差一个复常数。

2） 人在走路时，动态路径之间如果来自同一个身体部位（如头和躯干）的反射信号，因为它们的移动速度是相同的，所以是相干的（所以之前北大的Dy?namic_music的动态路径是非相干的理论是错的）。

3） 人在走路时，动态路径之间如果来自胳膊和腿，它们的速度通常是躯干的两倍，所以与躯干之间的反射信号是非相干的（因为躯干占身体比例的大部分，所以认为动态路径既有相干信号也有非相干信号）。

2 本文主要方法

窄带远场信号的数学模型为：

X （t） = As（t） + N （t）

其中，X （t） 为接收信号，A 为天线阵列的导向矢量，s（t） 为信号矩阵，N （t），信号的协方差矩阵的无偏估计为：

将上式代入得：R = E （X ? XH ） = AE （S ? SH ）AH + E （N ? NH ），式中E 为信号的期望。

根据空间谱估计理论，信号可分为信号空间和噪声空间：R = UΣUH = Us ΣsUsH + UN ΣNUNH。

我们又将信号空间分为静态信号空间和动态信号空间：R = UDΣDUDH + ULΣLULH + UN ΣNUNH。

因为静态路径间只相差复常数，所以，静态路径之间是相干的，所以用MUSIC算法估计信号到达角时，会合并为一条【参考Dy-music】。信号协方差的特征值表示不同路径的信号的功率大小。所以对于信号空间的特征值的最大的为静态信号（因为在LOS路径无遮挡的情况下，静态路径是最强的）。剩余的N-1， 为动态信号。即：

所以静态路径的到达角为： PMUSIC （θ静） = aH （θ ）ULU HL a（θ ） 来计算谱函数，通过寻求峰值来得到波达方向的估计值。

动态路径的到达角为： PMUSIC （θ动） = aH （θ ）UDU HD a（θ ） 来计算谱函数，通过寻求峰值来得到波达方向的估计值。

但是CSI只有三根天线，最多只能识别两条路径。对于典型的室内信号有6～8条，三根天线是远远不够的。每个天线有30个子载波，所以用不同子载波的对不同路径TOF引起的相位偏差来扩展天线。

第l 条路经在相邻不同天线引入的引起的相位偏移为d sin（θl ）/c。具体过程如图1所示。

第l 条传播路径相对于天线1，在第M 个天线的相移：-2πf （M - 1）d sin（θl ）/c

即：

Φ（θ ） = e-j2πd （M - 1）sin（θl ） × f/c

第l 条路经信号由天线引起的信号的导向矢量为：

第l 条路经在相邻不同子载波引入的引起的相位偏移为：2π（ fi - fi + 1 ）τl

第l 条传播对于等间隔OFDM子载波，第1条路径的飞行时间τl 在第n 个子载波处相对于天线的第一个子载波引入了2π（n - 1） fδ τl 的相移，其中fδ 是两个连续子载波之间的频率间隔，即：

Φ（τl ） = e-j2π（n - 1） × fδ τl

第l 条路经信号由子载波和天线共同引起的信号的导向矢量为：

即可用上面得到的导向矢量代入公式MUSIC算法的公式来估计静态路径和动态路径的角度。

3 仿真实验

为了验证本文算法的有效性，实验数据包括五个角度：theta=[-28° -26° 0° 4° 20°];其中-28°和-26°为相干的静态路径。0°和4°为相干的动态路径。20°为非相干的动态路径。静态路径的强度比较大（本文实验中，静态路径强度设为动态路径的2倍）。

从图2中可看出，MUSIC算法对相干信号完全失效，只检测到20°的一个信号。

相干的静态路径（-28°和-26°为相干的静态路径）合并为1条。如图3所示。

如图4所示，得到的动态路径的角度与原始设置的动态路径角度一致，而且可以实现相干信号的角度估计。0°和4°为相干的动态路径。20°为非相干的动态路径。

4 实际环境验证

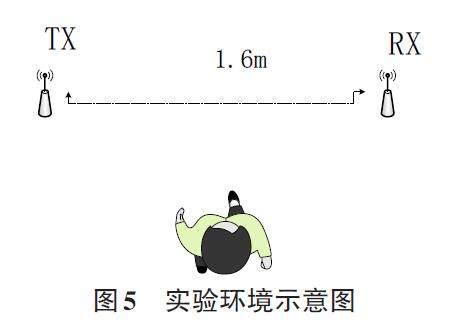
为了验证该算法的有效性。没有人的情况下采集了多组数据，用MUSIC算法得到静态路径的信号到达角，如图5所示。其中TX为Wi-Fi发送设备，RX为Wi-Fi接收设备，之间的间距为1.6米。然后人拿金属锡纸站在与天线直接连线平行的位置（相距一米）左右移动的情况，若使用上述动态和静态路径分离算法结果如下：

静态路径的到达角谱图如图7所示。从图中可看出静态路径结果与没有人时结果一致。与图6 结果一致。

动态路径的到达角谱图如图8所示：动态路径也与人在10°到80°的范围一致。

5 结论

提出了一种基于信号空间分解的动态，静态信号分离算法。充分分析了人体运动，产生的反射信号之间的相干性，该算法将信号协方差矩阵特征空间分解后，最大特征值和其对应的特征矢量形成的空间为静态信号空间，其余的为动态信号空间。再用信号空间的MUSIC算法来估计静态路径信号和动态路径信号的到达角。通过仿真实验和真实环境验证了本文算法的有效性。

【通联编辑：李雅琪】

基金项目：福建省教育厅青年科研项目（项目编号：JAT190011）